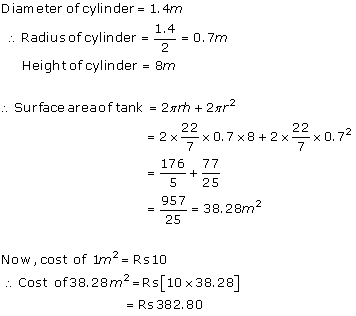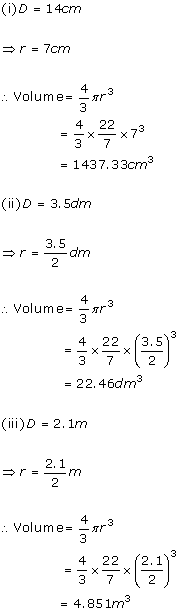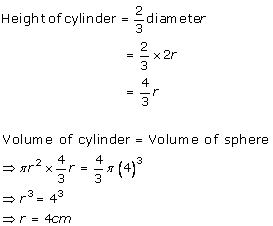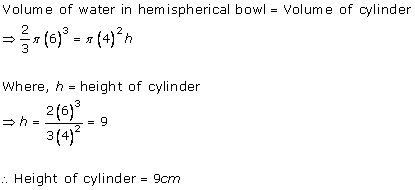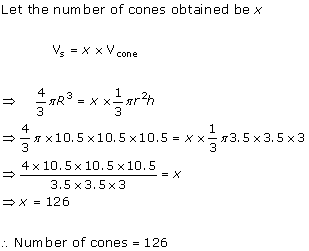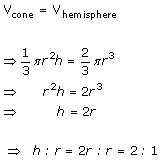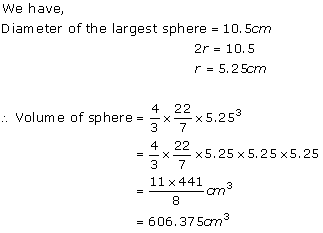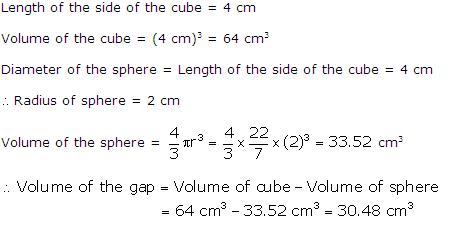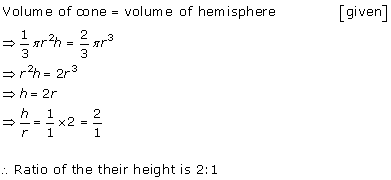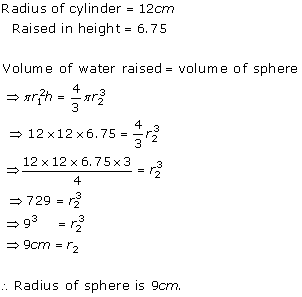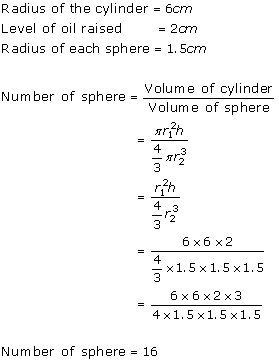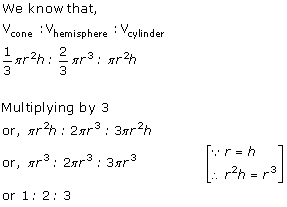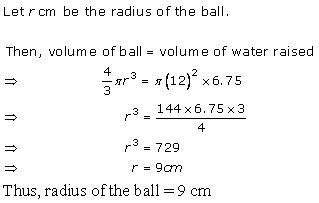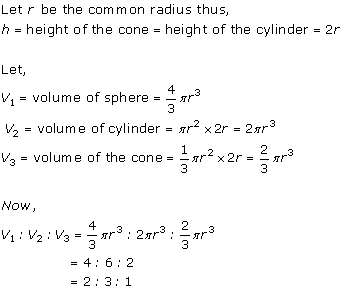Class 9 RD SHARMA Solutions Maths Chapter 21 - Surface Areas and Volume of a Sphere
Ex. 21.1
Ex. 21.2
21.26
21.27
Surface Areas and Volume of a Sphere Exercise Ex. 21.1
Solution 1
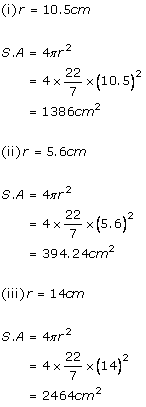
Solution 2
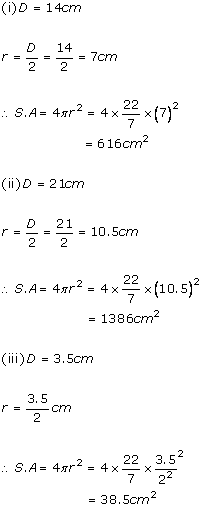
Solution 3
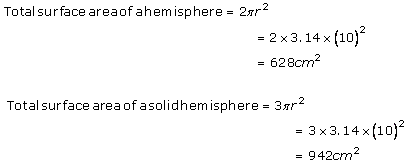
Solution 4

Solution 5

Solution 6

Solution 7
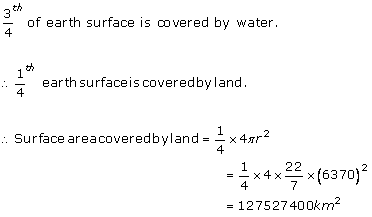
Solution 8
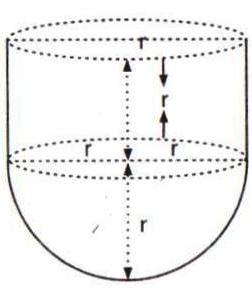

Solution 9
Solution 10
Solution 11
Solution 12

Solution 13

Surface Areas and Volume of A Sphere Exercise Ex. 21.2
Solution 1

Solution 2
Solution 3
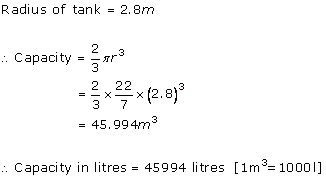
Solution 4
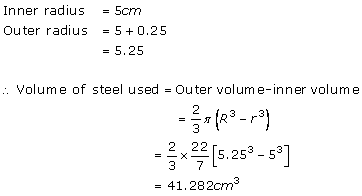
Solution 5
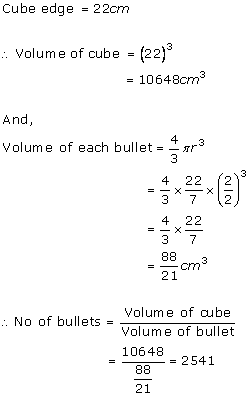
Solution 6
Solution 7
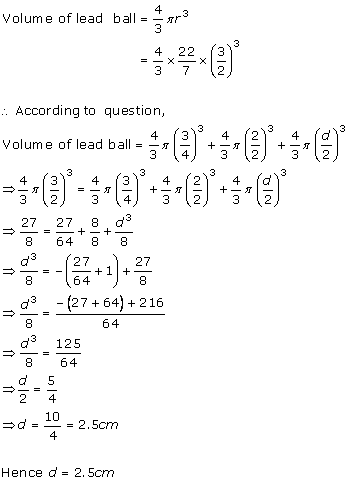
Solution 8
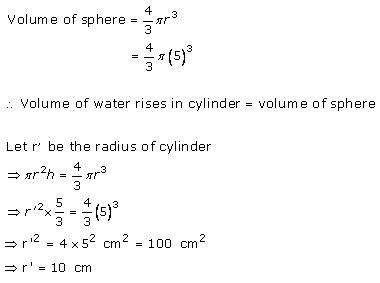
Solution 9
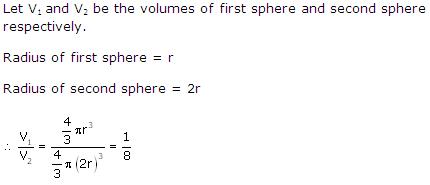
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
Solution 22
Inner radius (r1) of hemispherical tank = 1 m
Thickness of hemispherical tank = 1 cm = 0.01 m
Outer radius (r2) of hemispherical tank = (1 + 0.01) m = 1.01 m
Thickness of hemispherical tank = 1 cm = 0.01 m
Outer radius (r2) of hemispherical tank = (1 + 0.01) m = 1.01 m
Volume of iron used to make the tank = 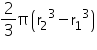
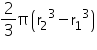

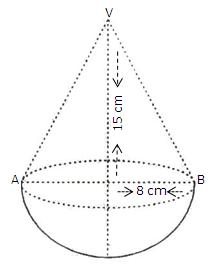
Solution 23
Radius (r) of capsule
Volume of spherical capsule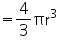
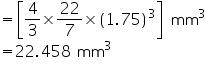
Thus, approximately 22.46 mm3 of medicine is required to fill the capsule.

Volume of spherical capsule
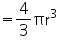
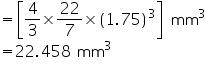
Thus, approximately 22.46 mm3 of medicine is required to fill the capsule.
Solution 24
Let diameter of earth be d. So, radius earth will be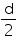 .
.
Then, diameter of moon will be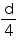 . So, radius of moon will be
. So, radius of moon will be 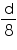 .
.
Volume of moon =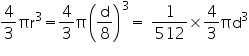
Volume of earth =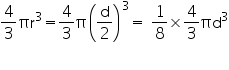
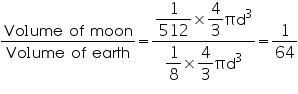
Thus, the volume of moon is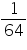 of volume of earth.
of volume of earth.
Then, diameter of moon will be
Volume of moon =
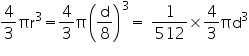
Volume of earth =
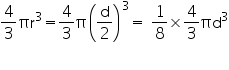
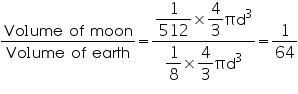
Thus, the volume of moon is
Solution 25
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
Solution 31
Solution 32
Surface Areas and Volume of a Sphere Exercise 21.26
Solution 1
Sphere has only one surface i.e. curved surface, so number of faces = 1
Hence, correct option is (a).
Solution 2
A hemisphere has two surfaces: one top surface and other curved surface.
T.S.A. = 2∏r2 + (∏r2) {Area of Top-face = ∏r2}
= 3∏r2
Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Surface Areas and Volume of a Sphere Exercise 21.27
Solution 10
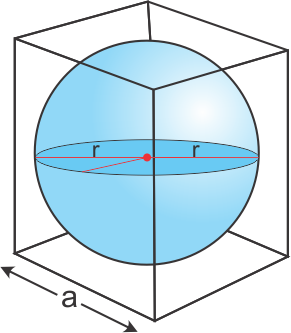

Solution 11

Solution 12

Radius of sphere = r
Sphere touches cylinder at Top, Base and Lateral Surface.
Then,
2r = height of cylinder = h
r = Radius of cylinder
Volume of cylinder = ∏r2h
=∏r2(2r)
= 2∏r3
Hence, correct option is (c).
Solution 13

Solution 14

Solution 15