Class 9 RD SHARMA Solutions Maths Chapter 1 - Number Systems
Ex. 1.1
Ex. 1.2
Ex. 1.3
Ex. 1.4
Ex. 1.5
Ex. 1.6
1.40
1.41
1.42
Number Systems Exercise Ex. 1.1
Solution 1
Yes zero is a rational number as it can be represented in the 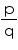 form, where p and q are integers and q
form, where p and q are integers and q 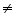 0 as
0 as 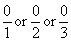 etc.
etc.
Concept Insight: Key idea to answer this question is "every integer is a rational number and zero is a non negative integer". Also 0 can be expressed in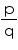 form in various ways as 0 divided by any number is 0. simplest is
form in various ways as 0 divided by any number is 0. simplest is 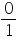 .
.
Concept Insight: Key idea to answer this question is "every integer is a rational number and zero is a non negative integer". Also 0 can be expressed in
Solution 2
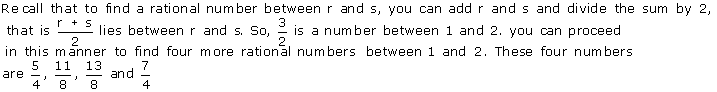
Solution 3
There are infinite rational numbers in between 3 and 4.
3 and 4 can be represented as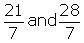 respectively.
respectively.
3 and 4 can be represented as
Now rational numbers between 3 and 4 are
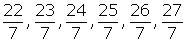
Concept Insight: Since there are infinite number of rational numbers between any two numbers so the answer is not unique here. The trick is to convert the number to equivalent
Solution 4
There are infinite rational numbers between 
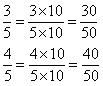
Now rational numbers between are 
Concept Insight: Since there are infinite number of rational numbers between any two numbers so the answer is not unique here. The trick is to convert the number to equivalent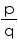 form by multiplying and dividing by the number at least 1 more than the rational numbers required.
form by multiplying and dividing by the number at least 1 more than the rational numbers required.
Alternatively for any two rational numbers a and b,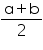 is also a rational number which lies between a and b.
is also a rational number which lies between a and b.
Alternatively for any two rational numbers a and b,
Solution 5
(i) False
(ii) True
(iii) False
(iv)True
(v) False
(vi) False
(ii) True
(iii) False
(iv)True
(v) False
(vi) False
Number Systems Exercise Ex. 1.2
Solution 1


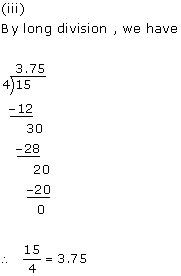
Solution 2
(i)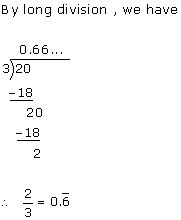
(ii)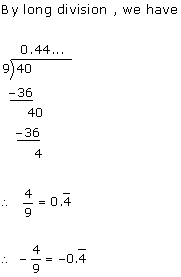
(iii)
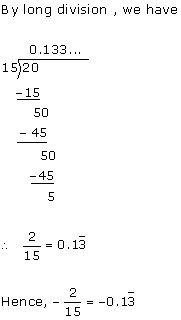
(iv)
(v)
(vi)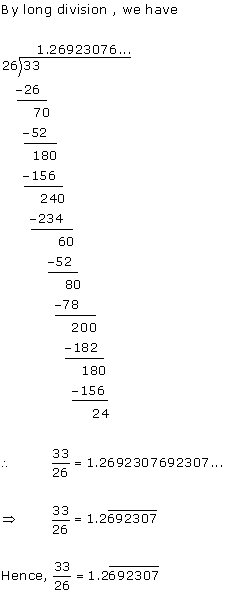
Solution 3

Number Systems Exercise Ex. 1.3
Solution 1

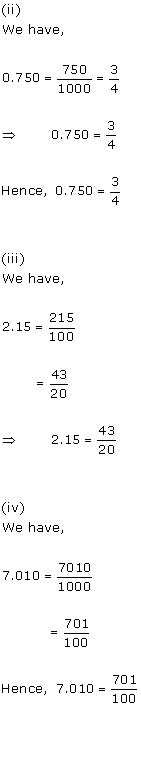

Solution 2
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Number Systems Exercise Ex. 1.4
Solution 1

Solution 2

Solution 3(i)
Solution 3(ii)

Solution 3(iii)

Solution 3(iv)

Solution 3(v)

Solution 3(vi)

Solution 3(vii)

Solution 3(viii)

Solution 3(ix)

Solution 3(x)
As decimal expansion of this number is non-terminating non recurring. So it is an irrational number.
Solution 3(xi)
Rational number as it can be represented in
Solution 3(xii)
0.3796
As decimal expansion of this number is terminating, so it is a rational number.
As decimal expansion of this number is terminating, so it is a rational number.
Solution 3(xiii)
As decimal expansion of this number is non terminating recurring so it is a rational number.
Solution 3(xiv)
Solution 4(i)

Solution 4(ii)

Solution 4(iii)

Solution 4(iv)

Solution 4(v)

Solution 4(vi)

Solution 5



Solution 6

Solution 7

Solution 8

Solution 9

Solution 10
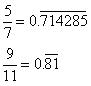
3 irrational numbers are -
0.73073007300073000073 ... ... ...
0.73073007300073000073 ... ... ...
0.75075007500075000075 ... ... ...
0.79079007900079000079 ... ... ...
0.79079007900079000079 ... ... ...
Concept Insight: There is infinite number of rational and irrational numbers between any two rational numbers. Convert the number into its decimal form to find irrationals between them.
Alternatively following result can be used to answer
Irrational number between two numbers x and y

Solution 11


Solution 12

Solution 13

Solution 14

Number Systems Exercise Ex. 1.5
Solution 1
(i) Real, rational, irrartional.
(ii) terminating, repeating.
(iii) terminating, non-terminating and reccuring.
(iv) rational, an irrational.
(ii) terminating, repeating.
(iii) terminating, non-terminating and reccuring.
(iv) rational, an irrational.
Solution 2
(i) True
(ii) True
(iii) False
Solution 3
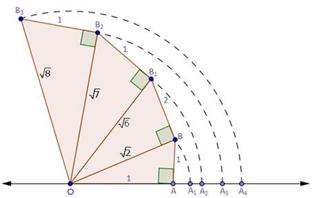
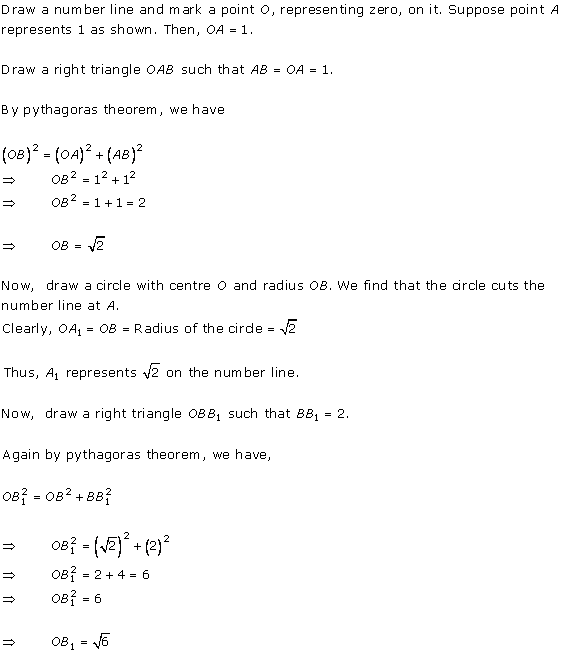

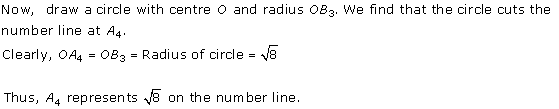
Solution 4
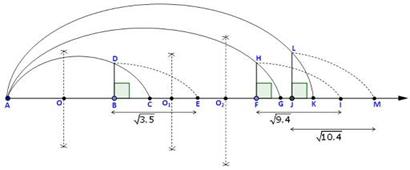


Number Systems Exercise Ex. 1.6
Solution 1

![]()
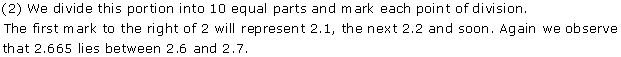
![]()
![]()
![]()


Solution 2


Number Systems Exercise 1.40
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8
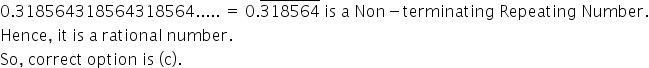
Solution 9

Number Systems Exercise 1.41
Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19
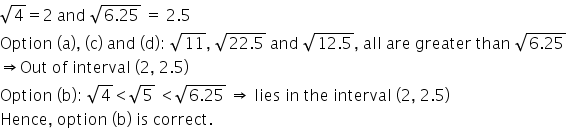
Solution 20

Number Systems Exercise 1.42
Solution 21


