Class 9 RD SHARMA Solutions Maths Chapter 24 - Measures of Central Tendency
Ex. 24.1
Ex. 24.2
Ex. 24.3
Ex. 24.4
24.21
24.22
Measures of Central Tendency Exercise Ex. 24.1
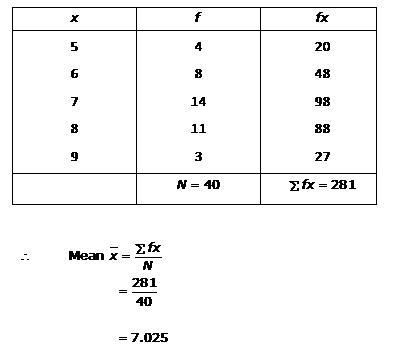
Solution 1
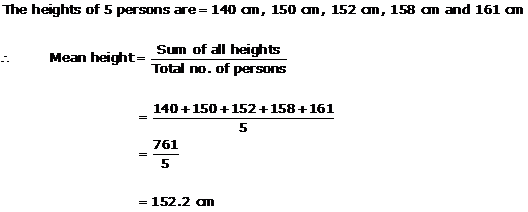
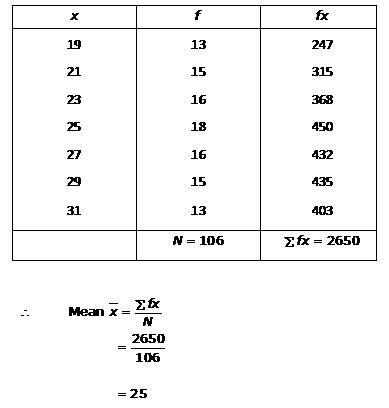
Solution 2
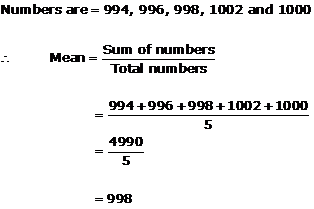
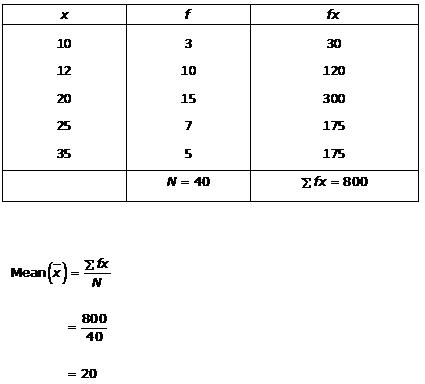
Solution 3
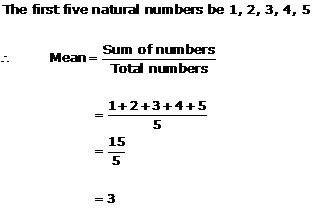
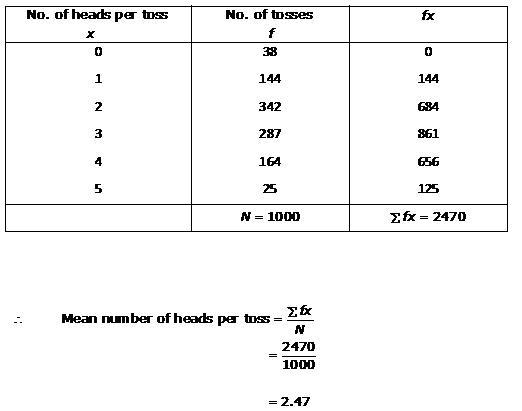
Solution 4
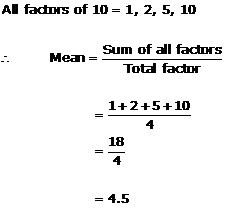
Solution 5
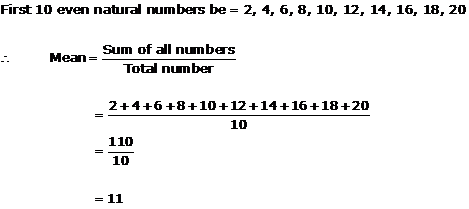
Solution 6
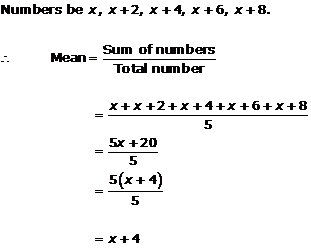
Solution 7
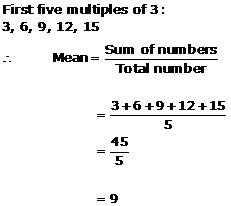
Solution 8

Solution 9
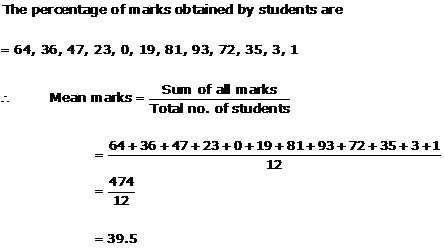
Solution 10
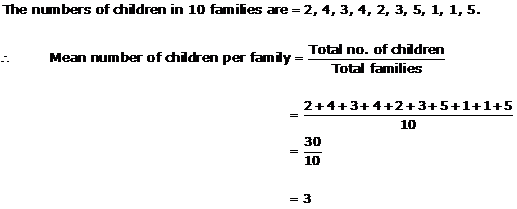
Solution 11
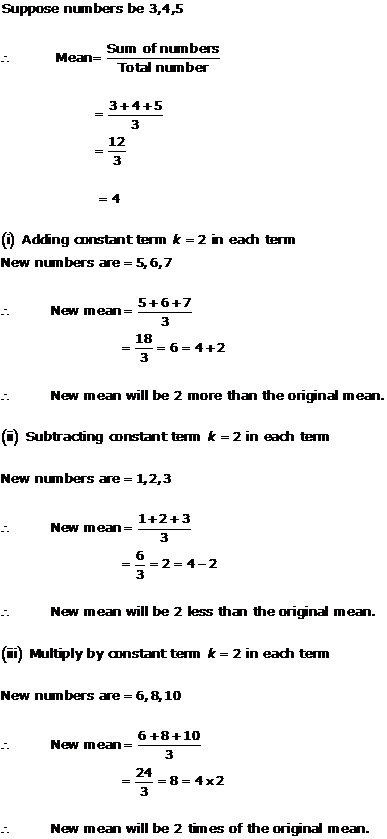
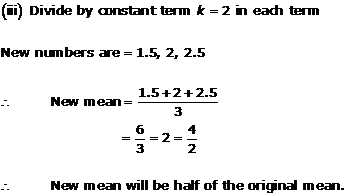
Solution 12
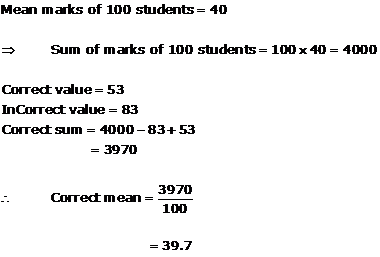
Solution 13
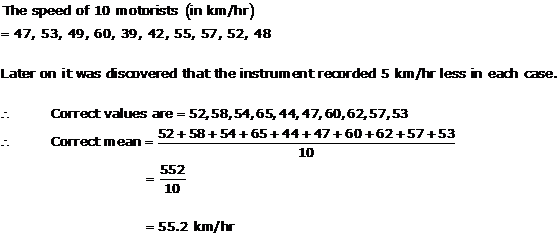
Solution 14

Solution 15
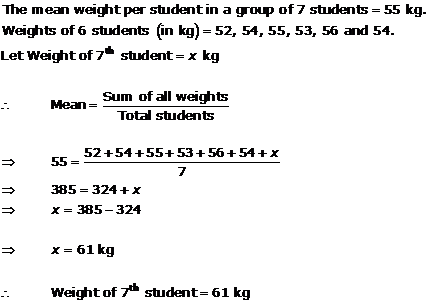
Solution 16

Solution 17
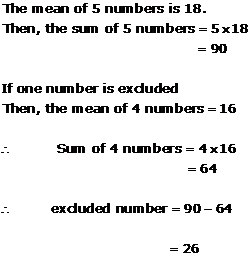
Solution 18
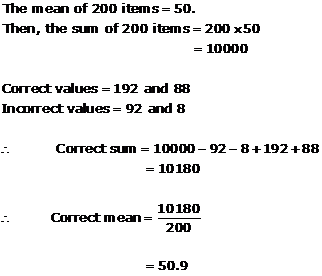
Solution 19
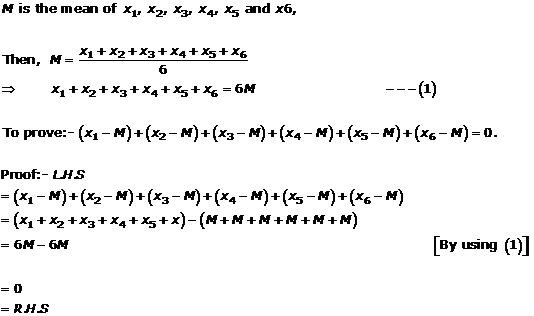
Solution 20
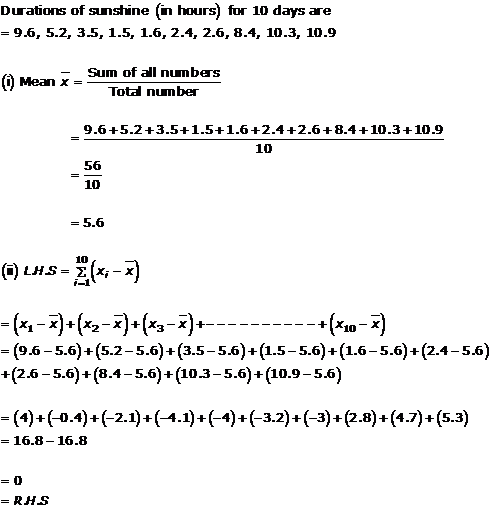
Solution 21
(i)
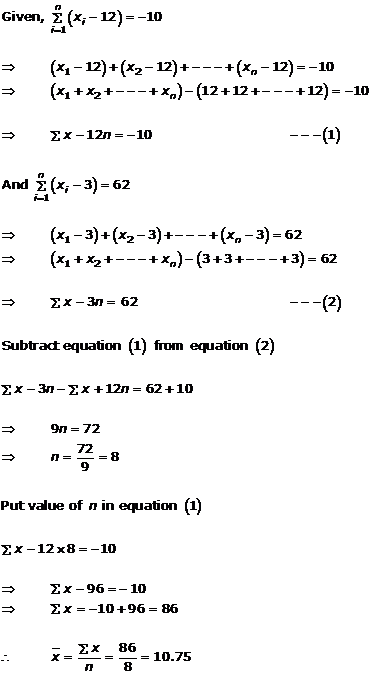
(ii)
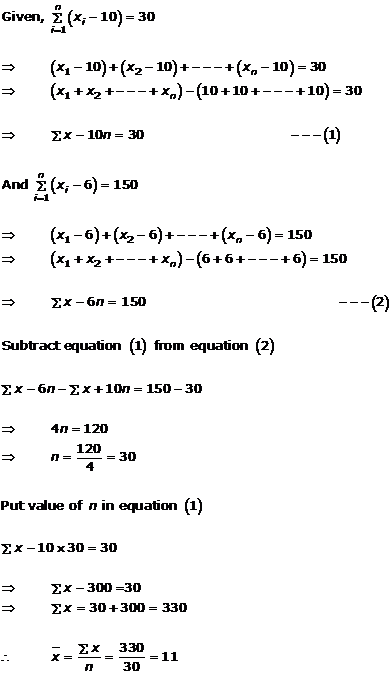
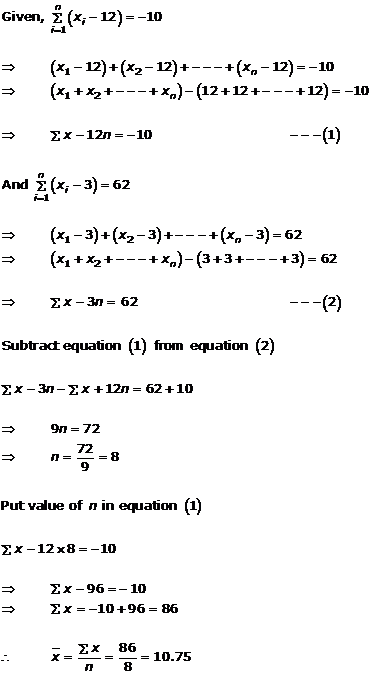
(ii)
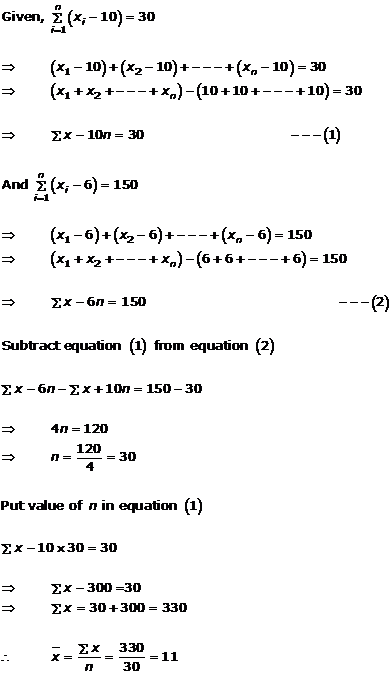
Solution 22

Solution 23
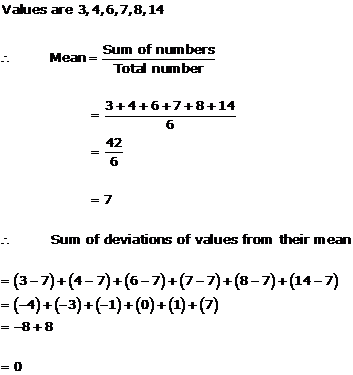
Solution 24
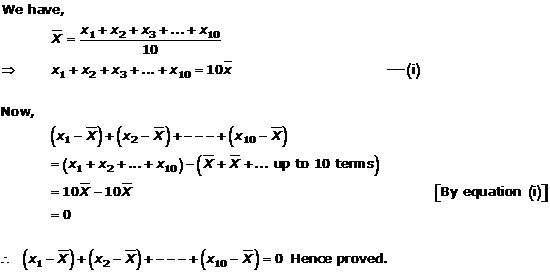
Measures of Central Tendency Exercise Ex. 24.2
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
| x | f | xf |
| 10 | 17 | 170 |
| 30 | f1 | 30f1 |
| 50 | 32 | 1600 |
| 70 | f2 | 70f2 |
| 90 | 19 | 1710 |
| N = 120 | 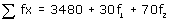 |

Measures of Central Tendency Exercise Ex. 24.3
Solution 1
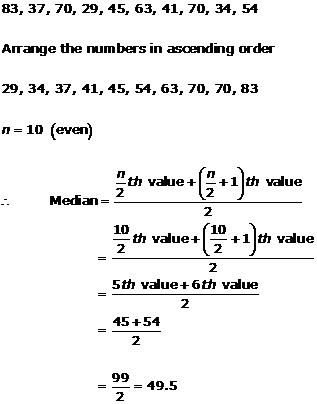
Solution 2
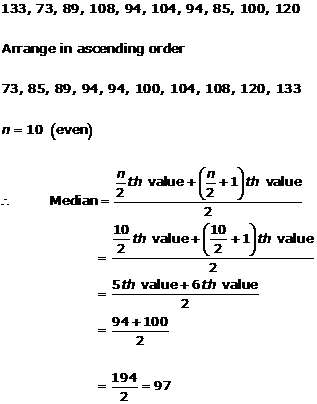
Solution 3
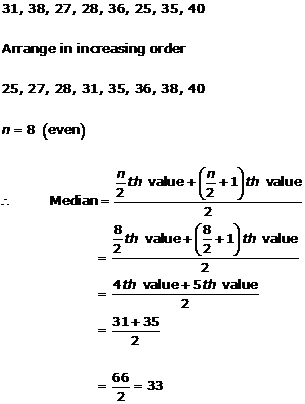
Solution 4
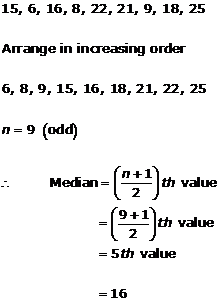
Solution 5
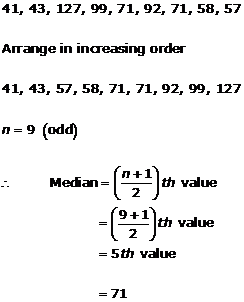
Solution 6
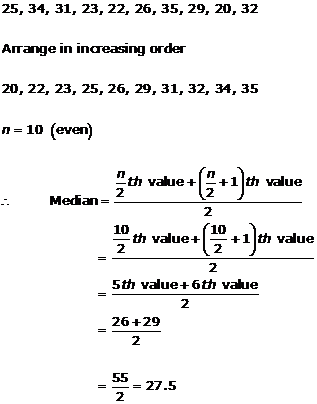
Solution 7
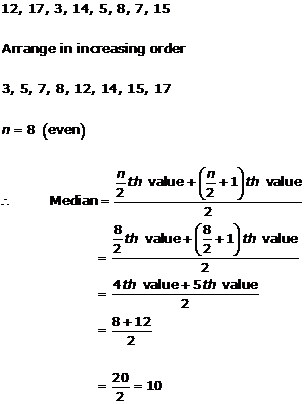
Solution 8
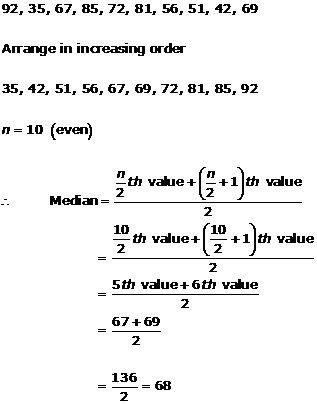
Solution 9

Solution 10
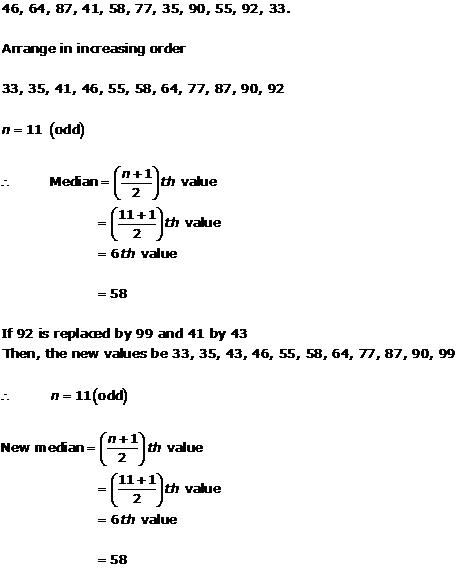
Solution 11
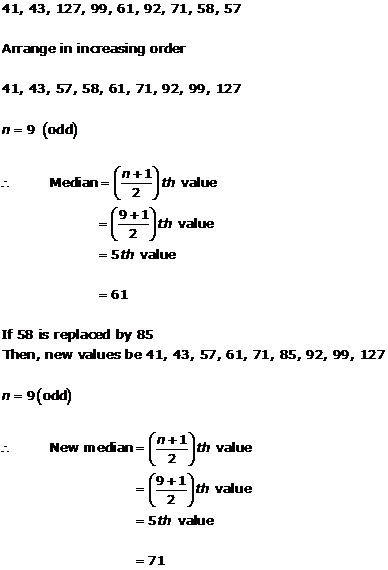
Solution 12
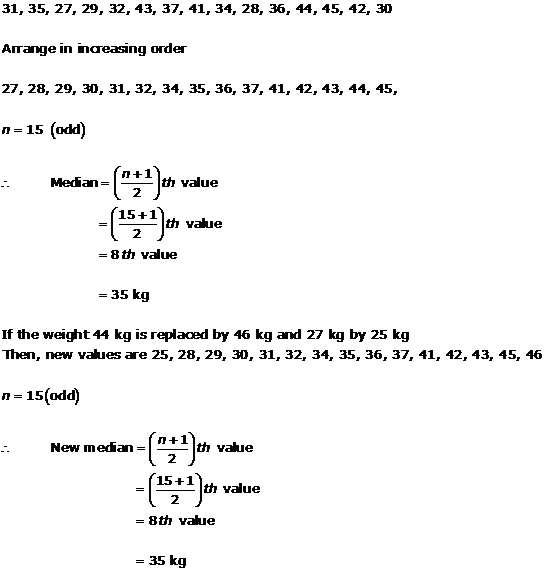
Solution 13

Measures of Central Tendency Exercise Ex. 24.4
Solution 1
Solution 2
Solution 3
Solution 4(i)
Arranging the data in an ascending order
14, 14, 14, 14, 17, 18, 18, 18, 22, 23, 25, 28
Here observation 14 is having the highest frequency i.e. 4 in given data. So, mode of given data is 14.
Solution 4 (ii)
Solution 5
Measures of Central Tendency Exercise 24.21
Solution 1
Range is not a measure of central value.
The difference between the highest value and the lowest value in the data set is called Range.
Hence, correct option is (b).
Solution 2

Measures of Central Tendency Exercise 24.22
Solution 3

Solution 4

Solution 5
| Mean | Median | Mode | |
| 2, 2, 2, 2, 4 | 12/5 = 2.4 | 2 | 2 |
| 1, 3, 3, 3, 5 | 15/5 = 3 | 3 | 3 |
| 1, 1, 2, 5, 6 | 15/5 = 3 | 2 | 1 |
| 1, 1, 1, 2, 5 | 10/5 = 2 | 1 | 1 |
From above table, data 1, 3, 3, 3, 5 has mean, median, mode all have same value, i.e. 3.
Hence, correct option is (b).
Solution 6

Solution 7

Solution 8

Solution 9
Most Frequent value is called mode.
Hence, correct option is (c).
Solution 10

Solution 11

Solution 12

Solution 13

Solution 24
The empirical Relation between mean, median and mode is
Mode = 3 Median - 2 mean
Hence, correct option is (a).
Solution 25