Class 12-science RD SHARMA Solutions Maths Chapter 1 - Relations
Relations Exercise MCQ
Solution 35
Given: R = {(1, 2)}
R is not reflexive as (1, 1), (2, 2), (3, 3) ∉ R.
Since (1, 2) ∈ R but (2, 1) ∉ R
Therefore, R is not symmetric.
Also, R is not transitive.
Solution 1

Solution 2
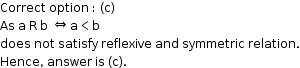
Solution 3

Solution 4

Solution 5
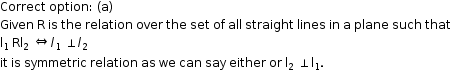
Solution 6

Solution 7

Solution 8

Solution 9
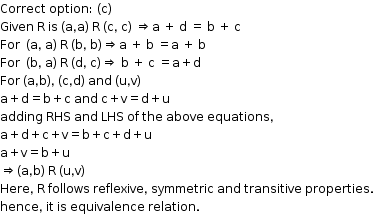
Solution 10

Solution 11

Solution 12

Solution 13
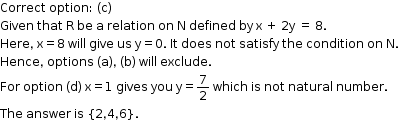
Solution 14

Solution 15

Solution 16
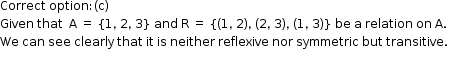
Solution 17
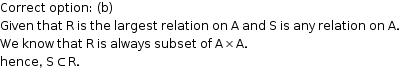
Solution 18

Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27

Solution 28

Solution 29

Solution 30
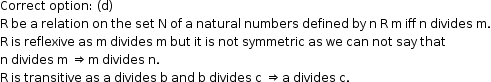
Solution 31
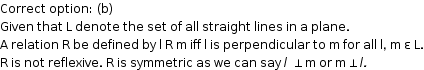
Solution 32

Solution 33

Solution 34

Relations Exercise Ex. 1.1
Solution 1(i)
Solution 1(ii)
Solution 1(iii)

Solution 1(iv)
Solution 2
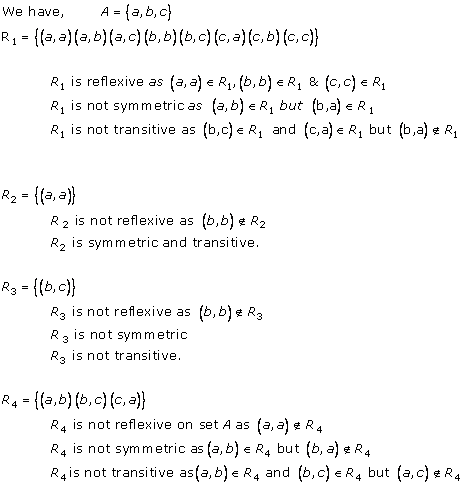
Solution 3(i)

Solution 3(ii)

Solution 3(iii)

Solution 4
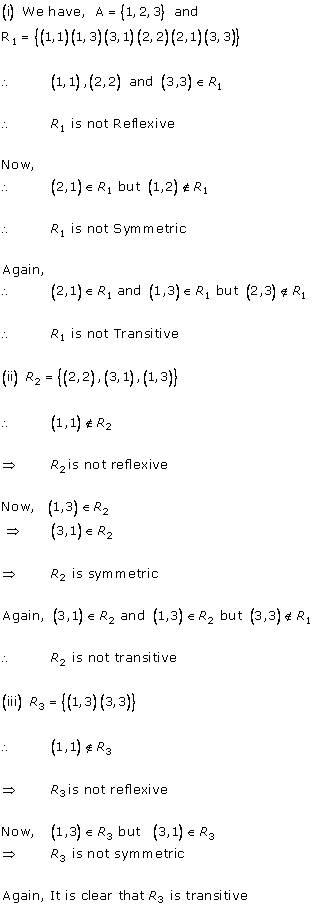
Solution 5(i)

Solution 5(ii)
Solution 5(iii)
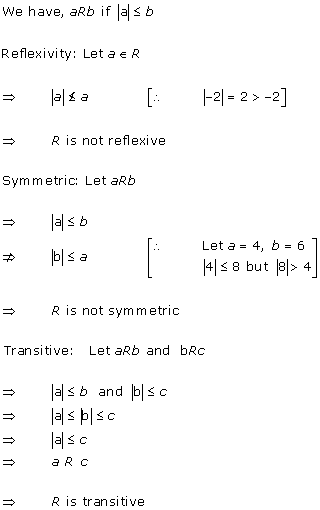
Solution 6

Solution 7(i)
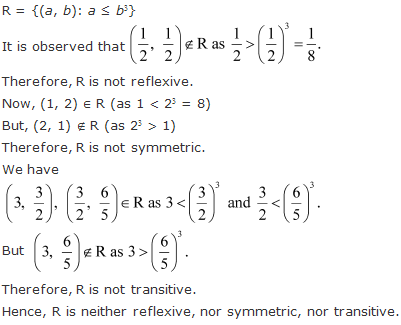
Solution 8
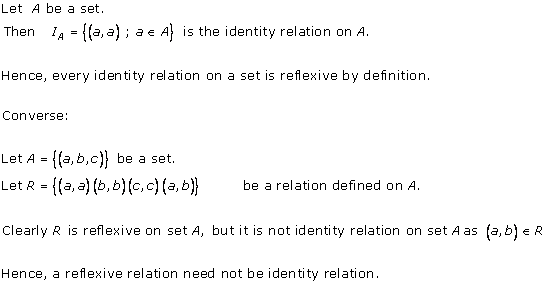
Solution 9
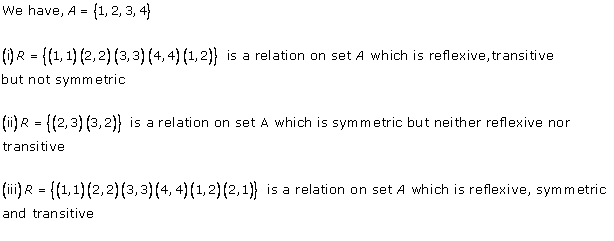
Solution 10

Solution 11

Solution 12

Solution 13
Solution 14
Solution 16

Solution 17
A relation R in A is said to be reflexive if aRa for all a∈A
R is said to be transitive if aRb and bRc ⇒ aRc
for all a, b, c ∈ A.
Hence for R to be reflexive (b, b) and (c, c) must be there in the set R.
Also for R to be transitive (a, c) must be in R because (a, b) ∈ R and (b, c) ∈ R so (a, c) must be in R.
So at least 3 ordered pairs must be added for R to be reflexive and transitive.
Solution 18
A relation R in A is said to be reflexive if aRa for all a∈A, R is symmetric if aRb ⇒ bRa, for all a, b ∈ A and it is said to be transitive if aRb and bRc ⇒ aRc for all a, b, c ∈ A.
• x > y, x, y ϵ N
(x, y) ϵ {(2, 1), (3, 1).......(3, 2), (4, 2)....}
This is not reflexive as (1, 1), (2, 2)....are absent.
This is not symmetric as (2,1) is present but (1,2) is absent.
This is transitive as (3, 2) ϵ R and (2,1) ϵ R also (3,1) ϵ R ,similarly this property satisfies all cases.
• x + y = 10, x, y ϵ N
(x, y)ϵ {(1, 9), (9, 1), (2, 8), (8, 2), (3, 7), (7, 3), (4, 6), (6, 4), (5, 5)}
This is not reflexive as (1, 1),(2, 2)..... are absent.
This only follows the condition of symmetric set as (1, 9)ϵR also (9, 1)ϵR similarly other cases are also satisfy the condition.
This is not transitive because {(1, 9),(9, 1)}ϵR but (1, 1) is absent.
• xy is square of an integer, x, y ϵ N
(x, y) ϵ {(1, 1), (2, 2), (4, 1), (1, 4), (3, 3), (9, 1), (1, 9), (4, 4), (2, 8), (8, 2), (16, 1), (1, 16)...........}
This is reflexive as (1,1),(2,2)..... are present.
This is also symmetric because if aRb ⇒ bRa, for all a,bϵN.
This is transitive also because if aRb and bRc ⇒ aRc for all a, b, c ϵ N.
• x + 4y = 10, x, y ϵ N
(x, y) ϵ {(6, 1), (2, 2)}
This is not reflexive as (1, 1), (2, 2).....are absent.
This is not symmetric because (6,1) ϵ R but (1,6) is absent.
This is not transitive as there are only two elements in the set having no element common.
Solution 7(ii)
Given: R = {(a, b) : a < b}
Clearly, 1 < 2
That is, (1, 2) ∈ R
But 2 ≮ 1
So, (2, 1) ∉ R
Therefore, R is not symmetric.
Let (a, b), (b, c) ∈ R
∴ a < b and b < c
∴ a < c
Therefore, (a, c) ∈ R
Thus, R is transitive.
Solution 15
Given: R = {(x, y) ∈ W × W such that x and y have at least one letter in common}
Clearly, (x, x) ∈ R as x and x have all the letters common.
Therefore, R is reflexive.
Now suppose, x and y have at least one letter in common.
So, y and x will also have at least one letter in common.
Therefore, R is symmetric.
Now take, x = Sun, y = Moon and z = Mars
Here, (x, y) ∈ R and (y, z) ∈ R as x and y have the letter "n" common whereas y and z have the letter "m" common.
But, x and z do not have any letter common.
Therefore, (x, z) ∉ R.
Thus, R is not transitive.
Relations Exercise Ex. 1.2
Solution 13
Given: R = {(a, b): a is divisor of b}
Any natural number "a" divides itself.
So, a is divisor of a.
Therefore, R is reflexive.
We know that 2 is divisor of 4.
So, (2, 4) ∈ R
But 4 does not divide 2, then (4, 2) ∉ R
Therefore, R is not symmetric.
As R is not symmetric.
Thus, R is not an equivalence relation.
Solution 18
To check reflexive:
Now, ![]() which is
real.
which is
real.
So, z1 R z1.
Therefore, R is reflexive.
To check symmetric:
Suppose z1 R z2
![]() is real
is real
Let ![]() where k is
real.
where k is
real.
Now, ![]()
Therefore, ![]() is real as -k
is real.
is real as -k
is real.
Therefore, R is symmetric.
To check transitive:
Suppose z1 R z2 and z2 R z3
![]() are real
are real
Let ![]()
![]()
![]() … (i)
… (i)
Now,  which is
real.
which is
real.
Thus, R is transitive.
Hence, R is an equivalence relation.
Solution 1

Solution 2
Solution 3

Solution 4

Solution 5

Solution 6

Solution 7
Solution 8

Also we need to find the set of all elements related to 1.
Since the relation is given by, R={(a,b):a=b}, and 1 is an element of A,
R={(1,1):1=1}
Thus, the set of all elements related to 1 is 1.
Solution 9

Solution 10

Solution 11

Solution 12

Solution 14
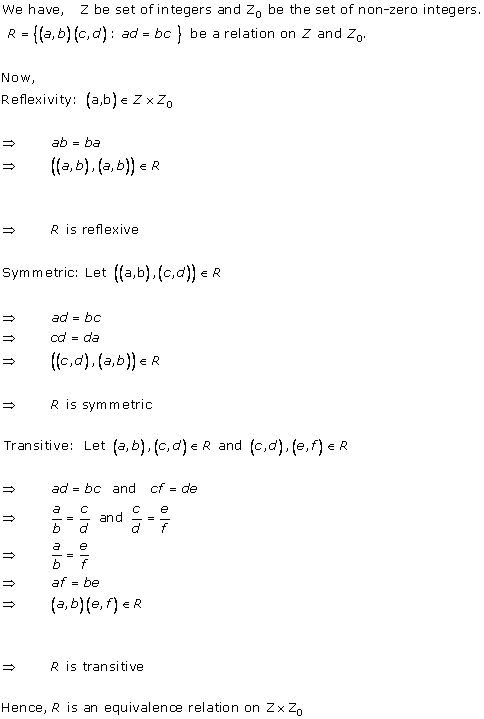
Solution 15

Solution 16
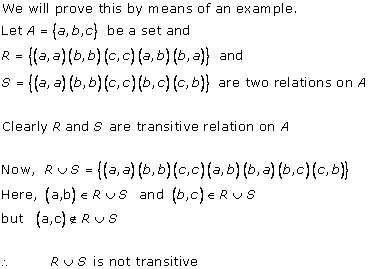
Relations Exercise Ex. 1VSAQ
Solution 1

Solution 2

Solution 3
![]()
Solution 4

Solution 5

Solution 6

Solution 7
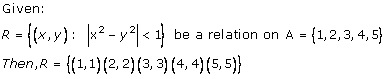
Solution 8
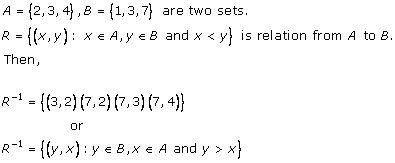
Solution 9
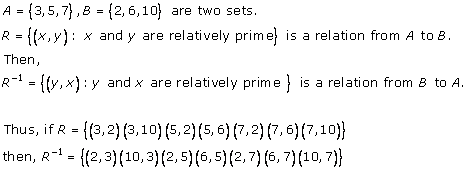
Solution 10

Solution 11

Solution 12
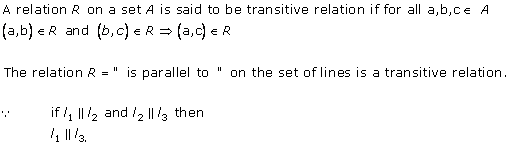
Solution 13
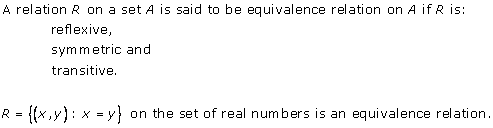
Solution 14

Solution 15
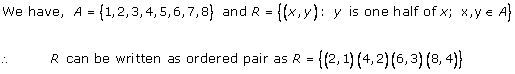
Solution 16

Solution 17
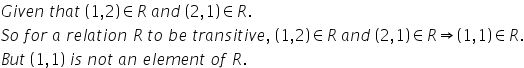
Solution 18
R = {(2,8),(3, 27)}
∴ The range set of R is {8, 27}.
Solution 19
a, b ∈ Z and R is given by R={(a, b): 2 divides a-b}.
The equivalence classes can be taken as [0], [1].
Note that, for 0 ≤ i ≤ 1, [i] = {2n + i : n ∈ Z}.
So equivalence class [0] = {2n : n ∈ Z}
It is clear that all the elements of equivalence class [0] are even.
Hence, equivalence class [0]={0, ± 2, ± 4, ± 6,...}
Solution 20
A relation R in A is said to be reflexive if aRa for all a∈A, R is symmetric if aRb ⇒ bRa, for all a, b ∈ A and it is said to be transitive if aRb and bRc ⇒ aRc for all a, b, c ∈ A. Any relation which is reflexive, symmetric and transitive is called an equivalence relation.
Given R is reflexive and transitive but not symmetric hence to make symmetric (3,1) added to R because (1,3) is already there. Hence (3, 1) is the single ordered pair which needs to be added to R to make it the smallest equivalence relation.
Solution 21
A relation R in A is said to be reflexive if aRa for all a∈A, R is symmetric if aRb ⇒ bRa, for all a, b ∈ A and it is said to be transitive if aRb and bRc ⇒ aRc for all a, b, c ∈ A
R is reflexive because {(0, 0),(1, 1),(2, 2),(3, 3)}∈R .
R is symmetric, because {(0,1),(0,3)}∈R and {(1,0),(3,0)} ∈ R .
but R is not transitive since for (1, 0) ∈ R and(0, 3) ∈ R whereas (1, 3) ∉ R.
Solution 22
A = {1, 2, 3, 4, 5} and R = {(a, b) :|a2 - b2 | < 8}
If a = 1 then from R we get b = 1, 2
If a = 2 then from R we get b = 1, 2, 3
If a = 3 then from R we get b = 2, 3, 4
If a = 4 then from R we get b = 3, 4
If a = 5 then from R we get b = 5
Hence R={(1,1),(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3), (4,4),(5,5)}
Solution 23
If a, b ∈ N then b must be an even integer so that a∈N
Hence only possible values for b are 2,4,6,8.
if b=2 , it gives a=12
if b=4 , it gives a=9
if b=6 , it gives a=6
if b=8 , it gives a=3
hence (a,b)ϵ{(3,8),(6,6),(9,4),(12,2)}
Solution 24
A relation R in A is said to be reflexive if aRa for all a∈A, R is symmetric if aRb ⇒ bRa, for all a, b ∈ A and it is said to be transitive if aRb and bRc ⇒ aRc for all a, b, c ∈ A. Any relation which is reflexive, symmetric and transitive is called an equivalence relation.
Hence smallest possible equivalence relation is {(1,1),(2,2),(3,3)}.
This relation satisfies all the conditions for an equivalence relation.







