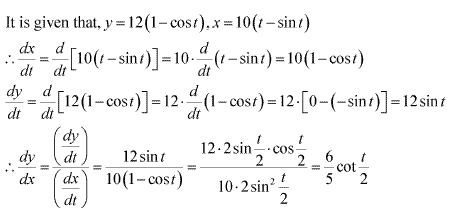Class 12-science RD SHARMA Solutions Maths Chapter 11 - Differentiation
Differentiation Exercise Ex. 11.1
Solution 1

Solution 2

Solution 3

Solution 4
Solution 5

Solution 6

Solution 7
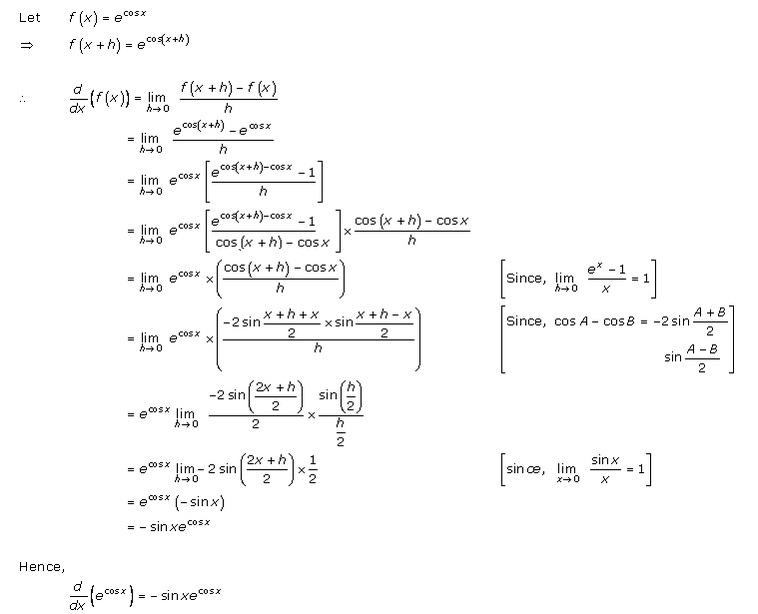
Solution 8

Solution 9

Solution 10


Differentiation Exercise Ex. 11.2
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10
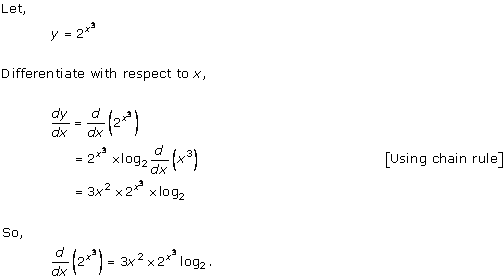
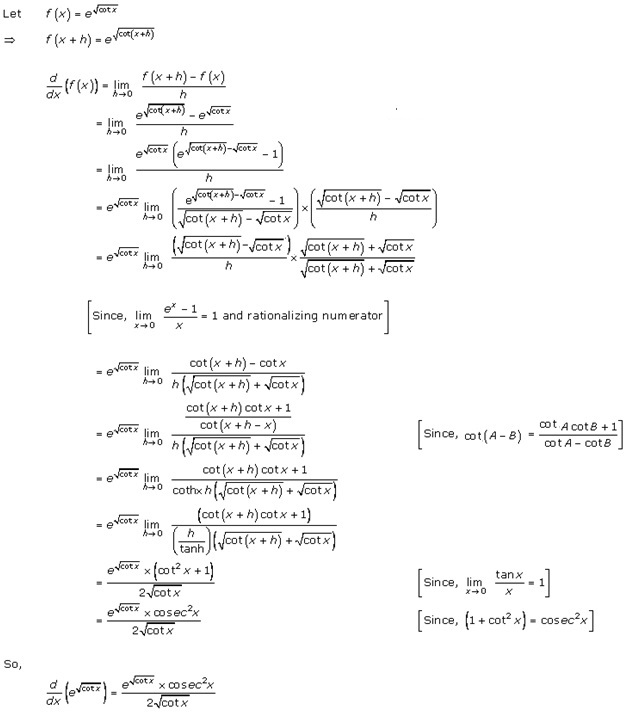
Solution 11
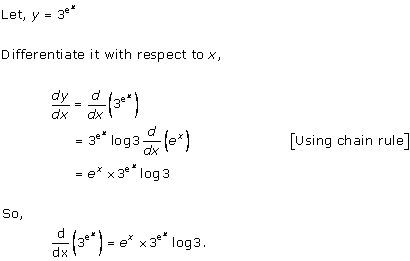
Solution 12

Solution 13
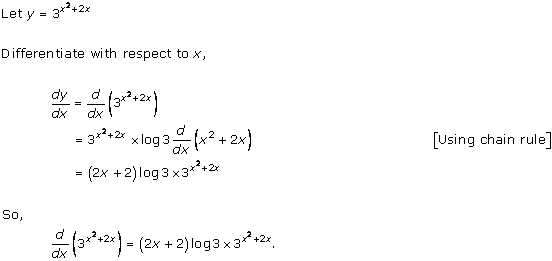
Solution 14

Solution 15

Solution 16


Solution 17

Solution 18
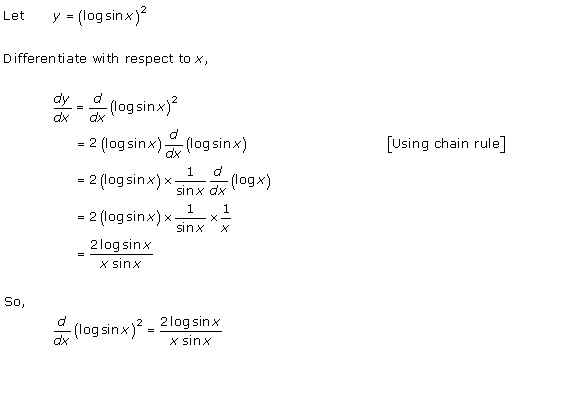
Solution 19

Solution 20

Solution 21
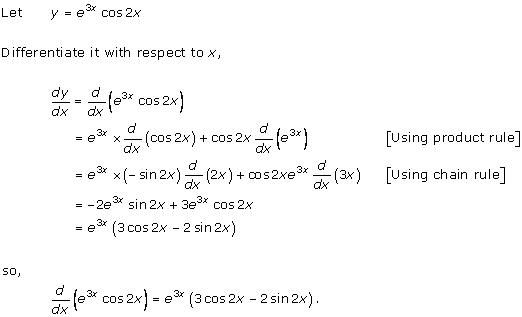
Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

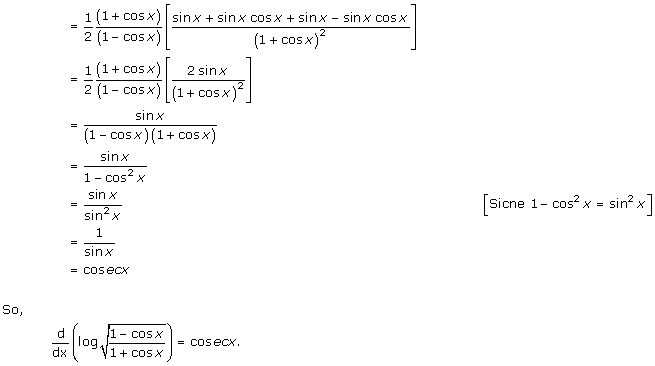
Solution 27

Solution 28

Solution 29

Solution 30

Solution 31

Solution 32

Solution 33

Solution 34

Solution 35

Solution 36
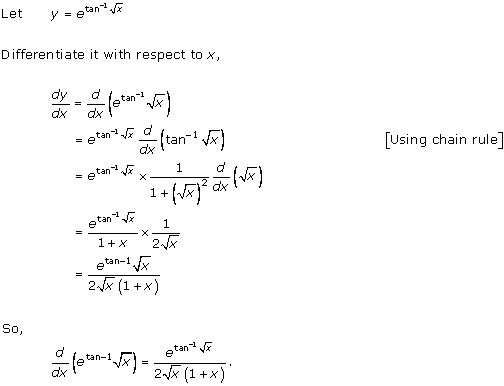
Solution 37

Solution 38

Solution 39

Solution 40

Solution 41

Solution 42

Solution 43

Solution 44

Solution 45



Solution 46

Solution 47

Solution 48

Solution 49

Solution 50

Solution 51

Solution 52

Solution 53

Solution 54

Solution 55

Solution 56

Solution 57
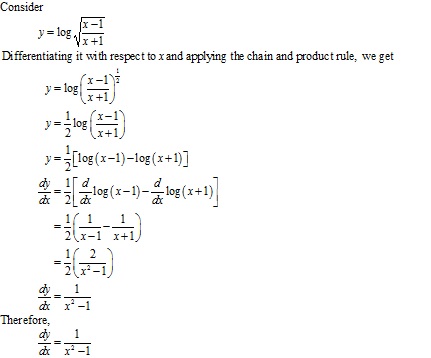
Solution 58

Solution 59
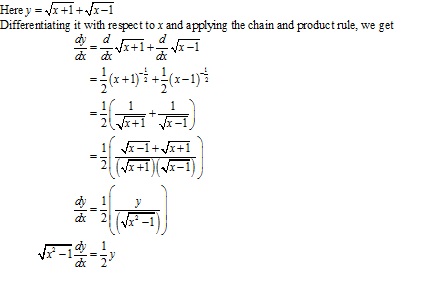
Solution 60
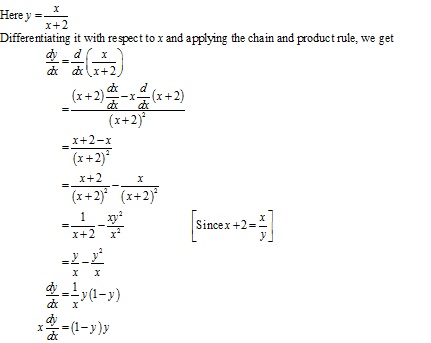
Solution 61
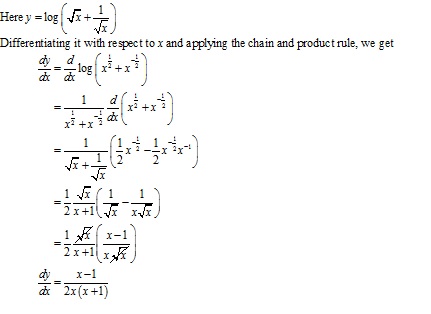
Solution 62
Given: ![]()
Differentiating w.r.t x, we get
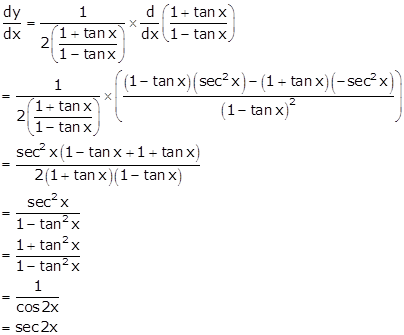
Hence, ![]()
Solution 63

Solution 64

Solution 65

Solution 66
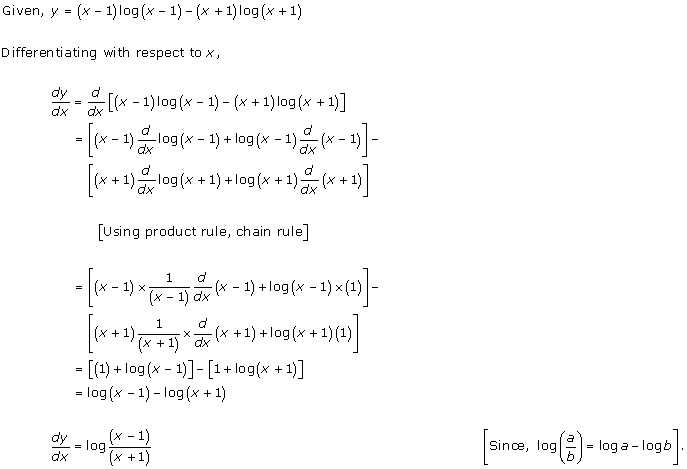
Solution 67

Solution 68

Solution 69

Solution 70

Solution 71

Solution 72

Solution 73

Solution 74

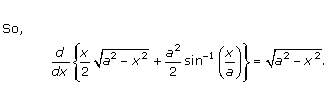
Solution 75
Given: ![]()
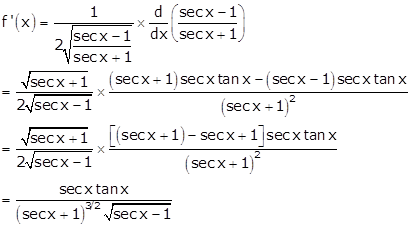
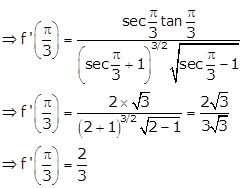
Solution 76
Given: ![]()
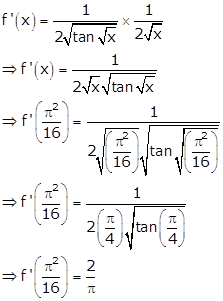
Differentiation Exercise Ex. 11.3
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10
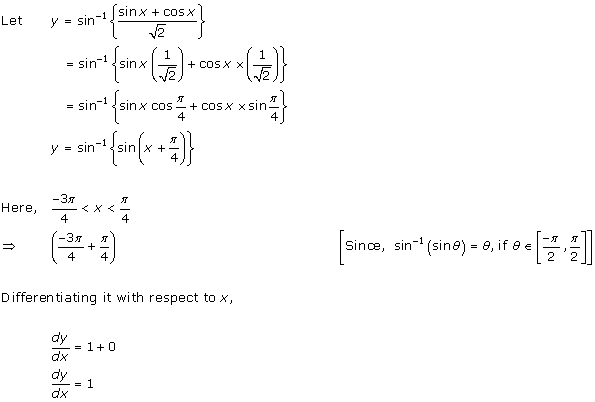
Solution 11

Solution 12
Let ![]()
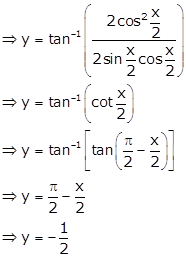
Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20

Solution 21
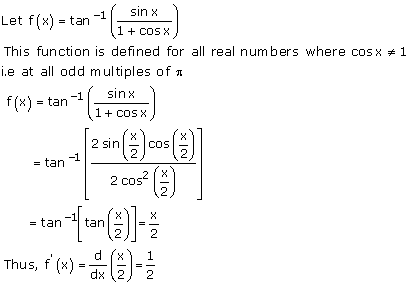
Solution 22

Solution 23

Solution 24
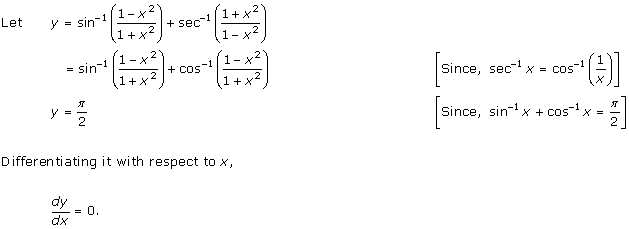
Solution 25
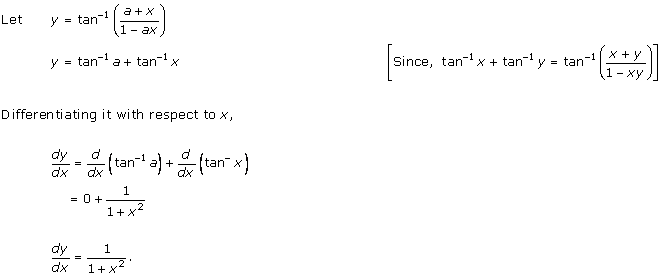
Solution 26

Solution 27

Solution 28

Solution 29

Solution 30
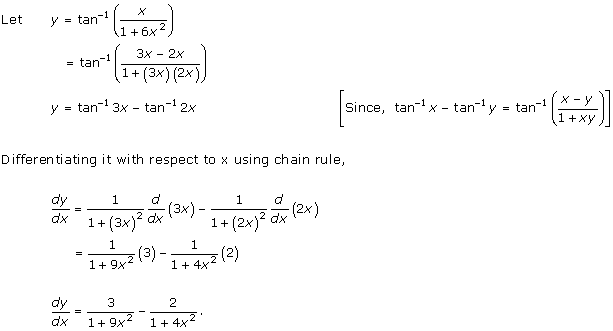
Solution 31

Solution 32
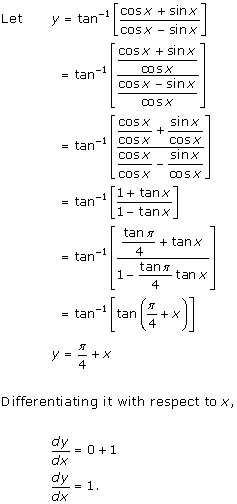
Solution 33

Solution 34
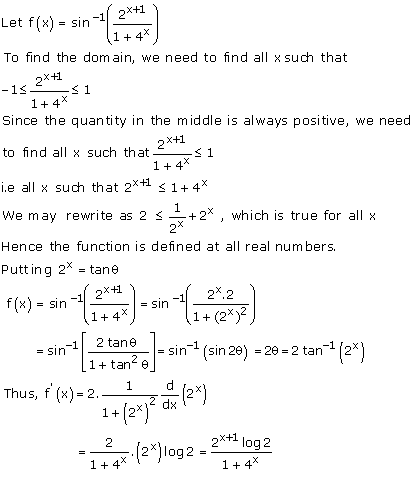
Solution 35

Solution 36

Solution 37(i)
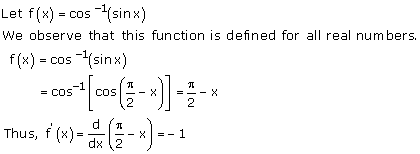
Solution 37(ii)

Solution 38
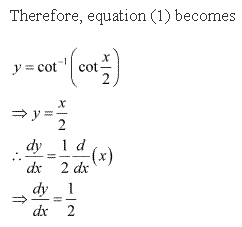
Solution 39

Solution 40
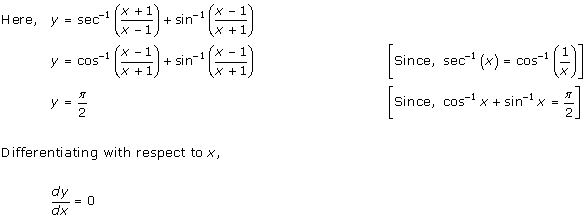
Solution 41

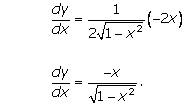
Solution 42

Solution 43
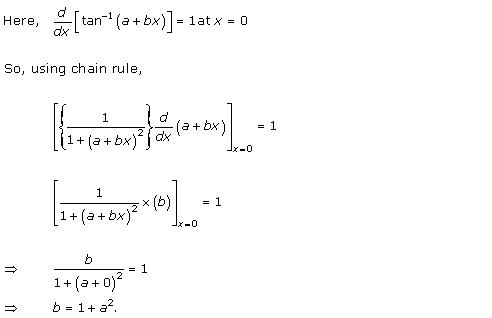
Solution 44

Solution 45

Solution 46
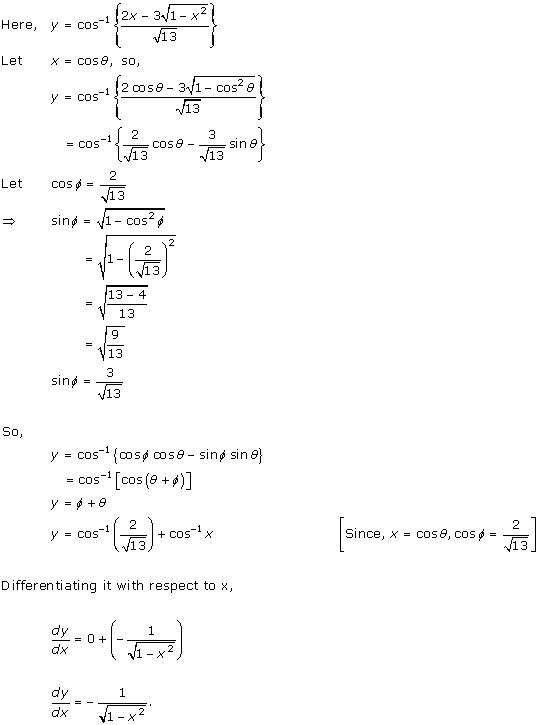
Solution 47
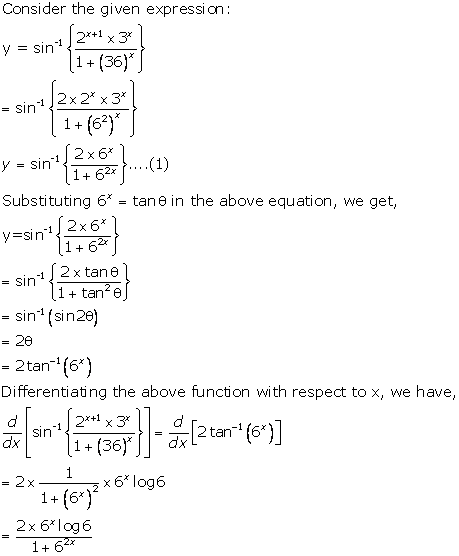
Solution 48
Given: ![]() ………. (i)
………. (i)
Let ![]()
From (i), we get
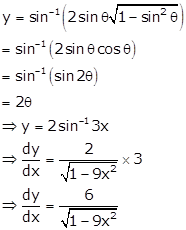
Differentiation Exercise Ex. 11.4
Solution 1

Solution 2

Solution 3
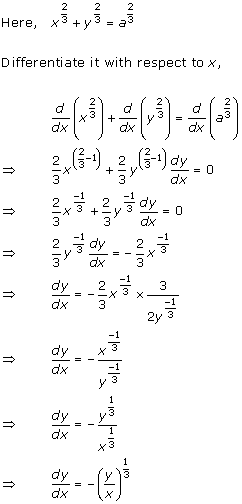
Solution 4

Solution 5
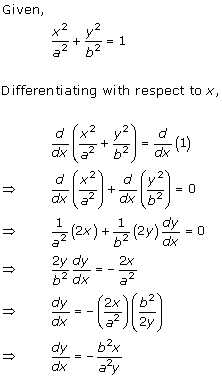
Solution 6

Solution 7
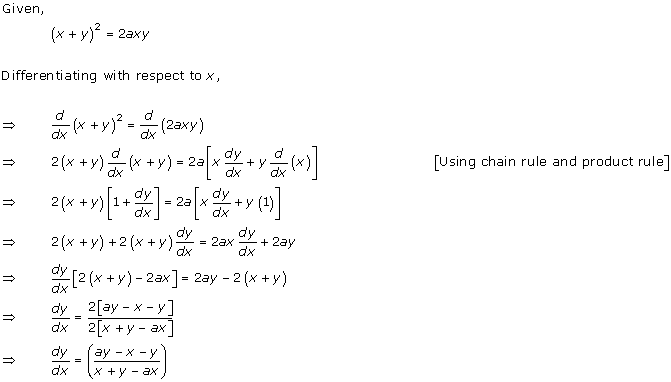
Solution 8
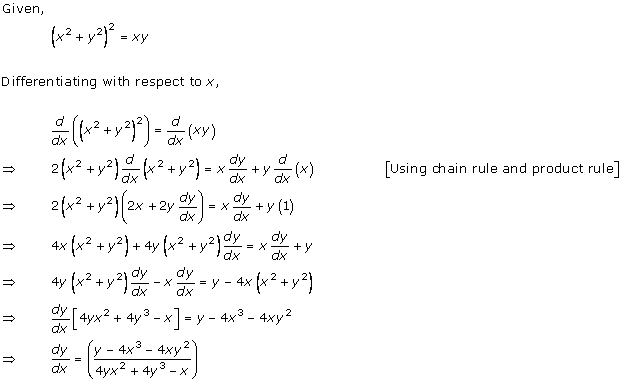
Solution 9
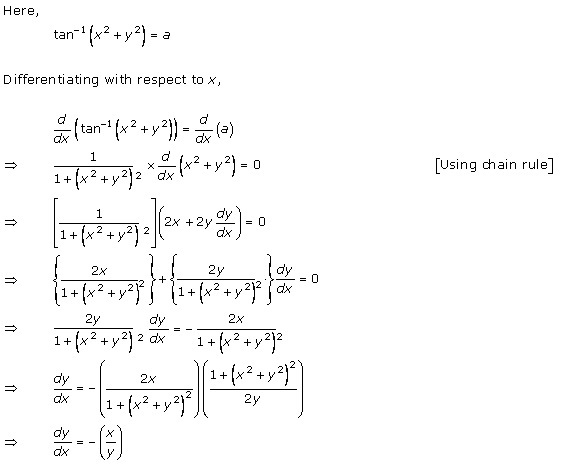
Solution 10

Solution 11
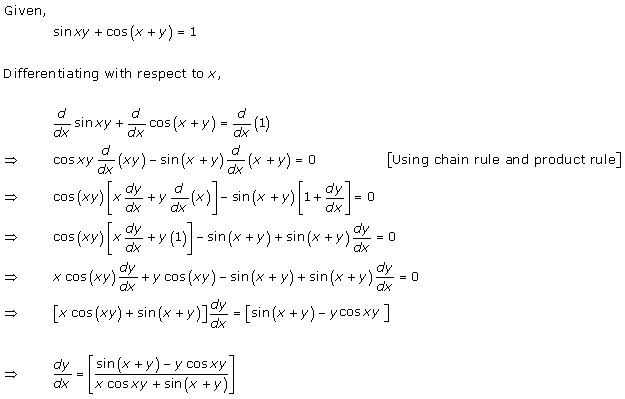
Solution 12

Solution 13

Solution 14
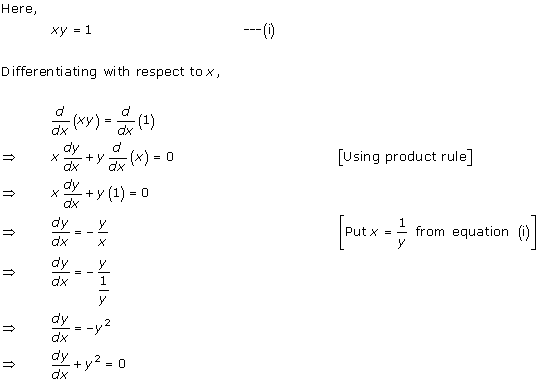
Solution 15

Solution 16

Solution 17

Solution 18
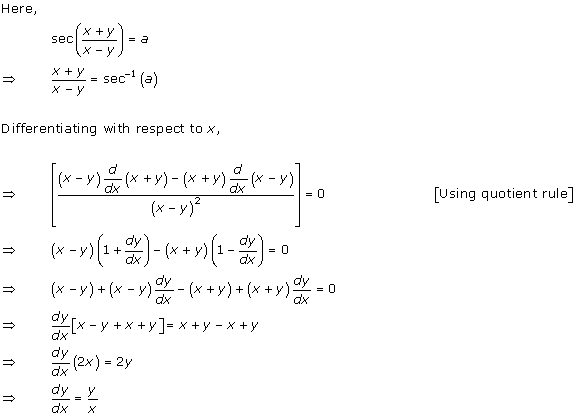
Solution 19
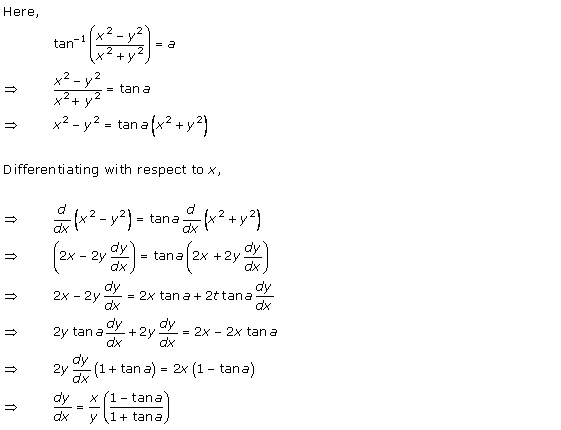
Solution 20

Solution 21

Solution 22

Solution 23
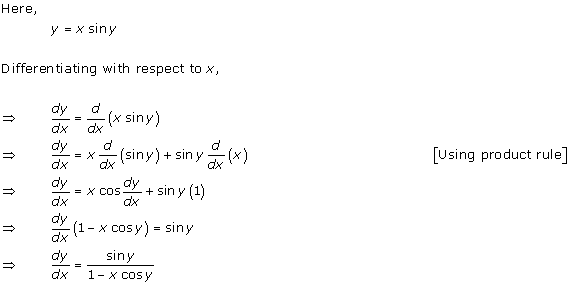
Solution 24

Solution 25

Solution 26

Solution 27

Solution 28
Solution 29
Given: ![]()
Differentiating w.r.t x. we get
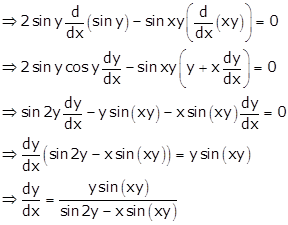
When x =1 and ![]() we get
we get
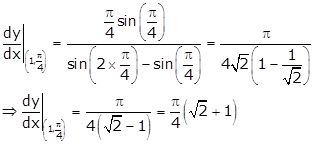
Solution 30
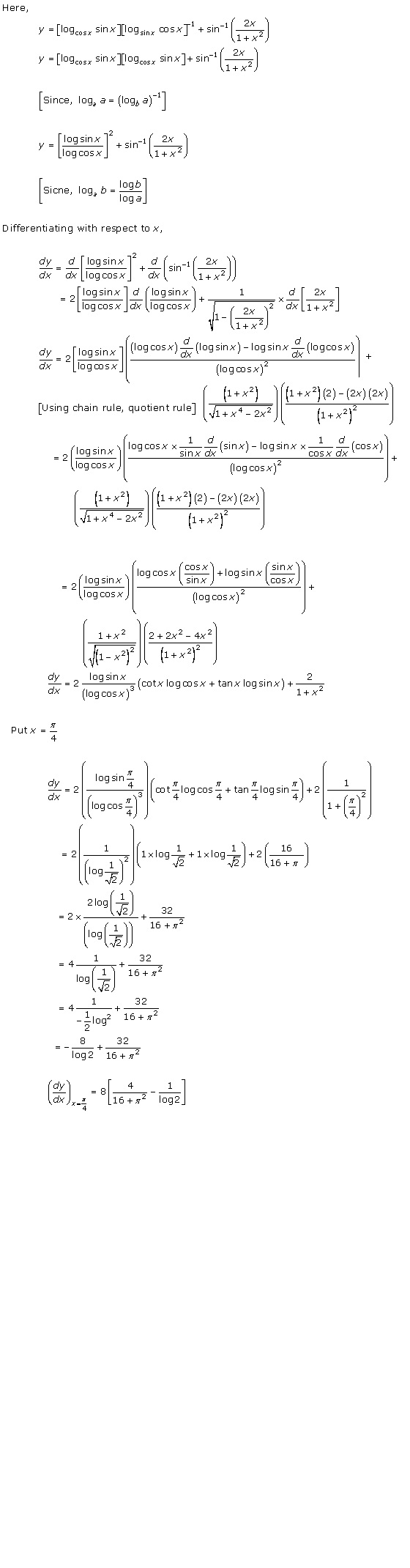
Solution 31

Differentiation Exercise Ex. 11.5
Solution 1

Solution 2
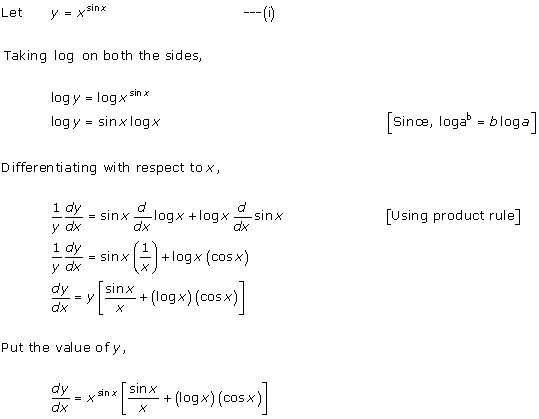
Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13
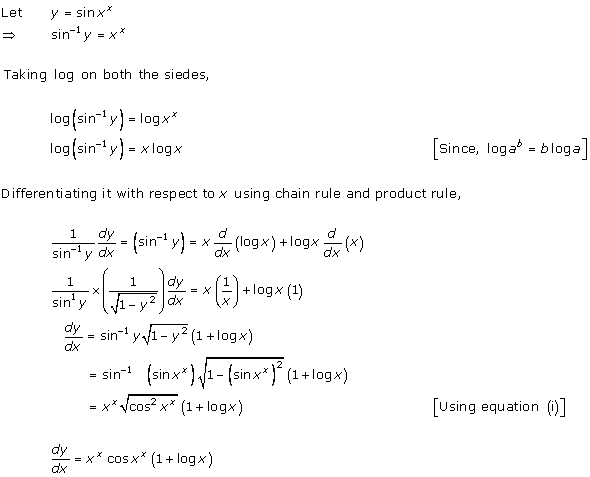
Solution 14

Solution 15

Solution 16

Solution 17

Solution 18(i)

Solution 18(ii)

Solution 18(iii)


Solution 18(iv)


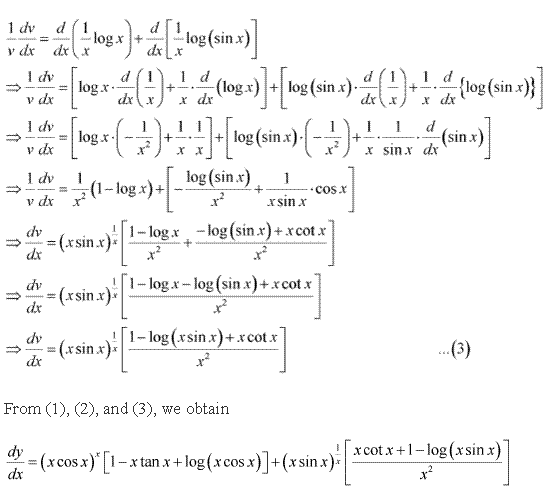
Solution 18(v)

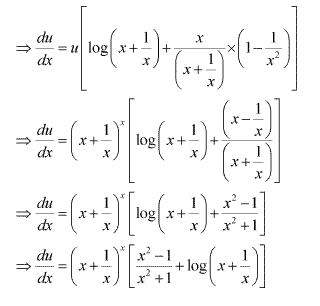

Solution 18(vi)

Solution 18(vii)

Solution 18(viii)


Solution 19

Solution 20
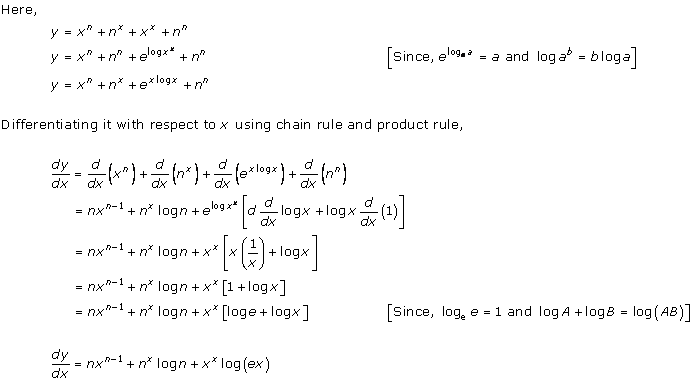
Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27

Solution 28
Given: ![]()
Let ![]()
![]()
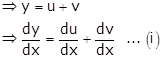
Differentiating 'u' w.r.t x, we get
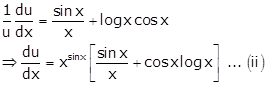
Differentiating 'v' w.r.t x, we get
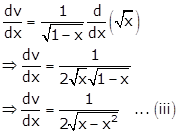
From (i), (ii) and (iii), we get
![]()
Solution 29(i)

Solution 29(ii)

Solution 30

Solution 31

Solution 32

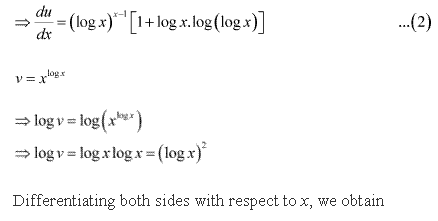
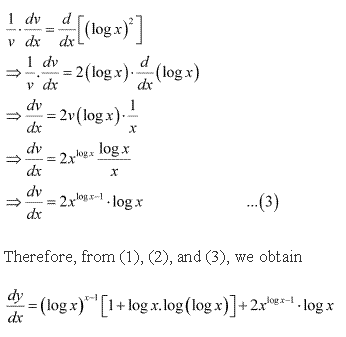
Solution 33

Solution 34

Solution 35

Solution 36

Solution 37

Solution 38

Solution 39
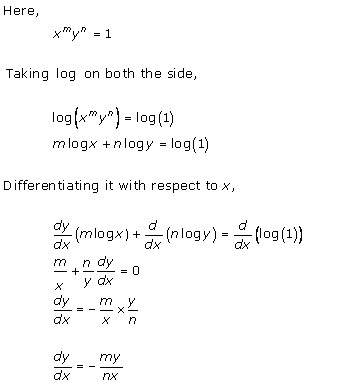
Solution 40

Solution 41

Solution 42

Solution 43

Solution 44
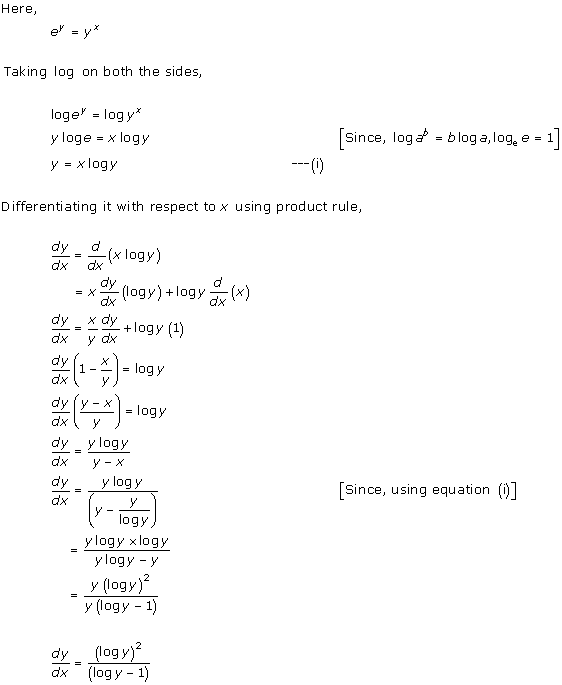
Solution 45

Solution 46
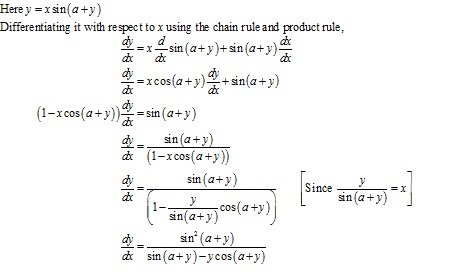
Solution 47

Solution 48

Solution 49

Solution 50

Solution 51

Solution 52

Solution 53

Solution 54
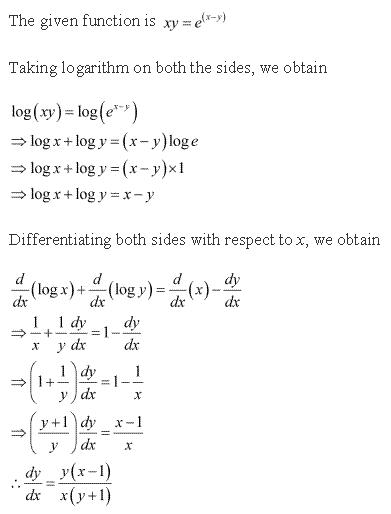
Solution 55

Solution 56
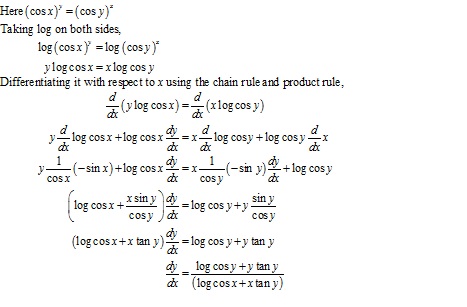
Solution 57

Solution 58

Solution 59
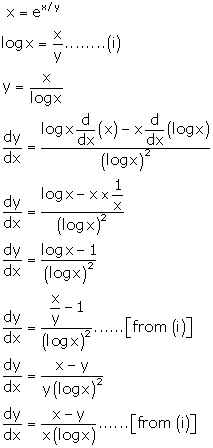
Solution 60
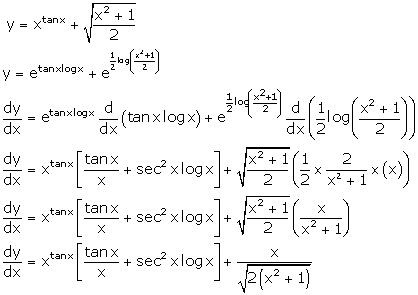
Solution 61
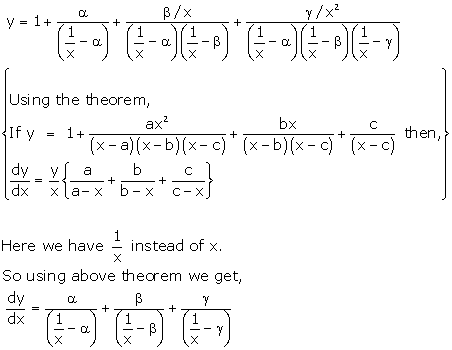
Solution 62
Given: ![]()
Let ![]()
![]()
Taking log on both the sides of equation (i), we get
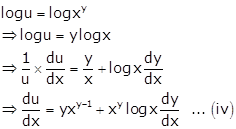
Taking log on both the sides of equation (ii), we get
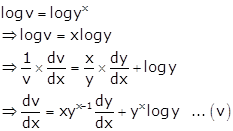
Differentiating (iii) w.r.t x, we get
![]()
Using (iv) and (v), we have
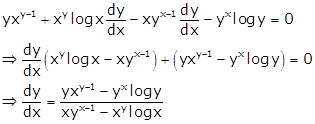
Differentiation Exercise Ex. 11.6
Solution 1
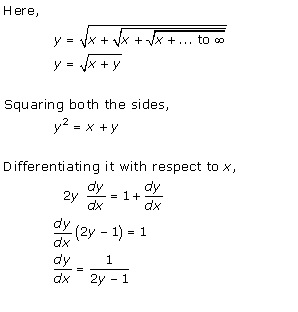
Solution 2
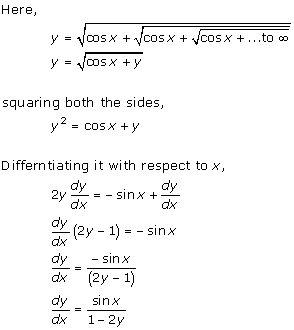
Solution 3

Solution 4

Solution 5

Solution 6

Solution 7


Solution 8

Differentiation Exercise Ex. 11.7
Solution 1
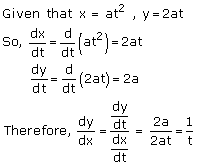
Solution 2

Solution 3
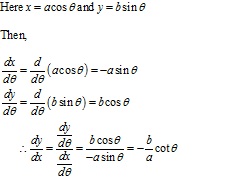
Solution 4

Solution 5
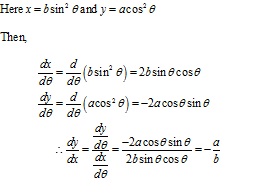
Solution 6
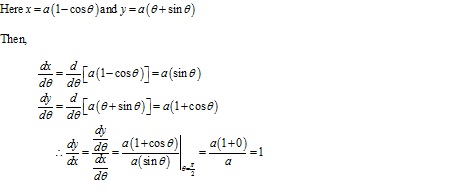
Solution 7
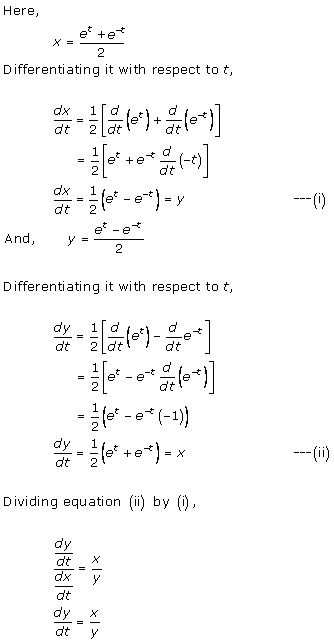
Solution 8


Solution 9
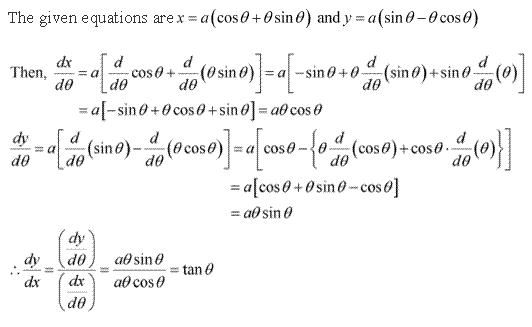
Solution 10


Solution 11


Solution 12

Solution 13


Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19
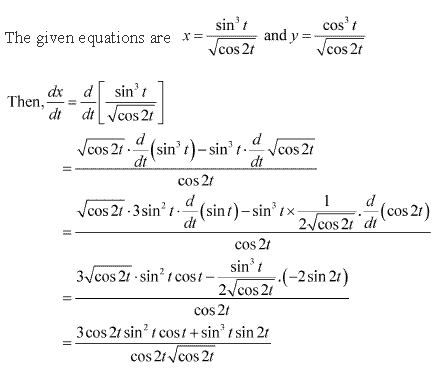
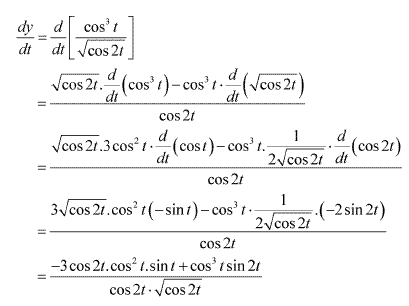

Solution 20

Solution 21


Solution 22
Solution 23
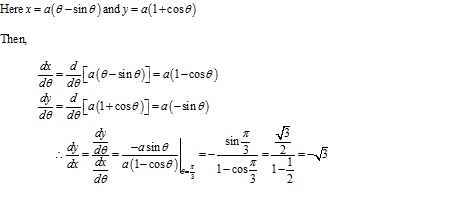
Solution 24

Solution 25

Solution 26

Solution 27

Solution 28
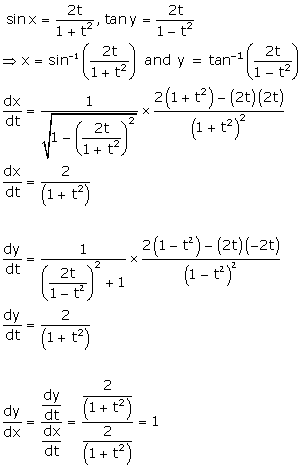
Solution 29
Given: ![]()
Differentiate 'x'
w.r.t ![]() , we get
, we get
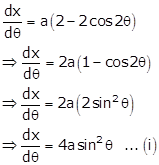
Differentiate 'y'
w.r.t ![]() , we get
, we get
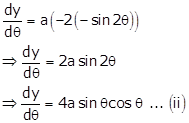
Dividing (ii) by (i), we get
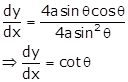
At ![]()
![]()
Differentiation Exercise Ex. 11.8
Solution 1
We need to find 
Let ![]()
So, we need to
find ![]()
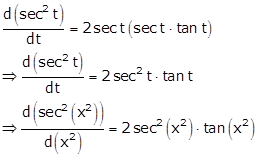
Solution 2

Solution 3

Solution 4(i)

Solution 4(ii)

Solution 5(i)


Solution 5(ii)

Solution 5(iii)

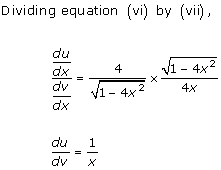
Solution 6

Solution 7(i)

Solution 7(ii)

Solution 8

Solution 9

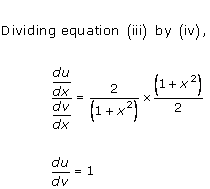
Solution 10


Solution 11


Solution 12

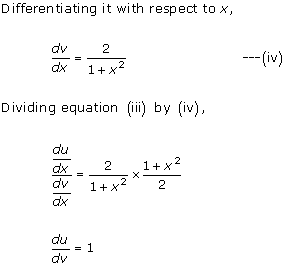
Solution 13

Solution 14
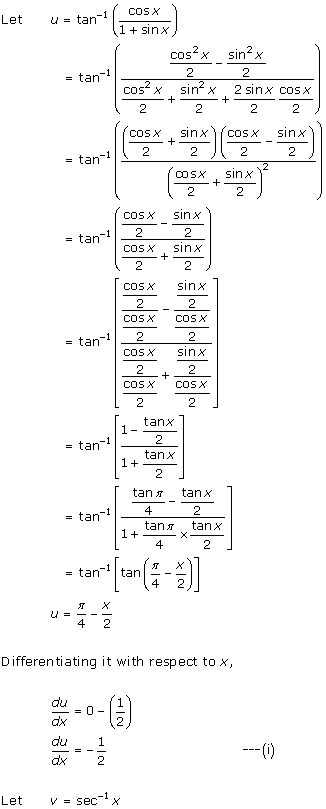
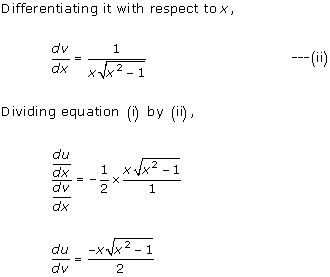
Solution 15

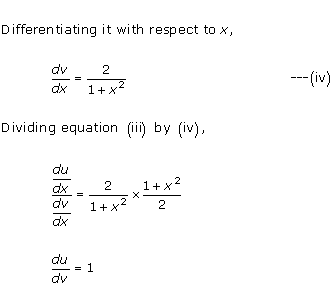
Solution 16

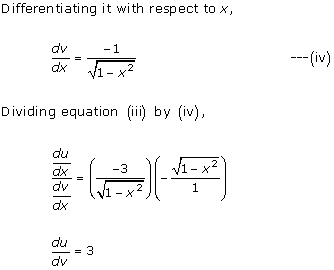
Solution 17


Solution 18


Solution 19


Solution 20

Solution 21
We need to find 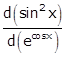
Let ![]()
Differentiating 'u' and 'v' w.r.t x, we get
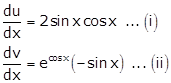
Dividing (i) by (ii), we get
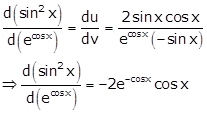
Differentiation Exercise MCQ
Solution 1
Correct option: (d)

Solution 2
Correct option: (c)
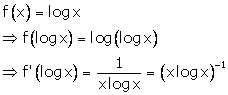
Solution 3
Correct option: (a)

Solution 4
Correct option: (d)
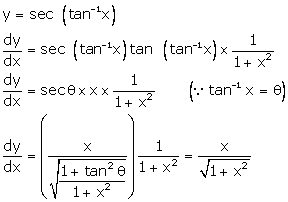
Solution 5
Correct option: (d)
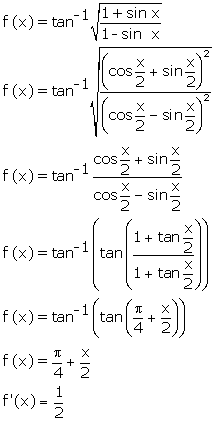
Solution 6
Correct option: (a)
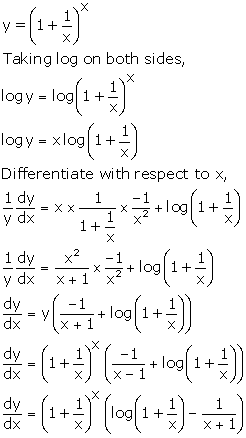
Solution 7
Correct option: (d)

Solution 8
Correct option: (c)
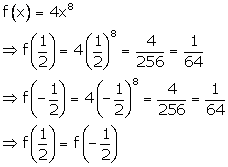
Solution 9
Correct option: (d)

Solution 10
Correct option:(a)

Solution 11
Correct option: (a)
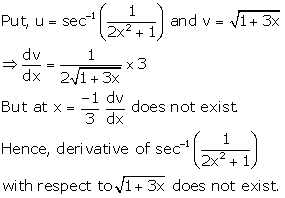
Solution 12
Correct option: (c)

Solution 13
Correct option: (d)

Solution 14
Correct option: (d)

Solution 15
Correct option: (b)
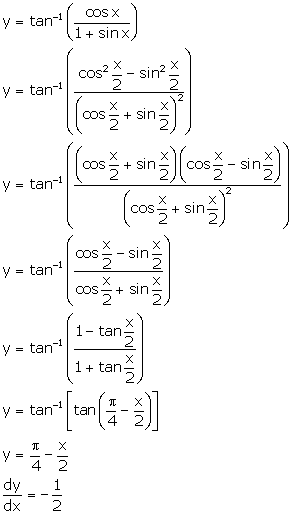
Solution 16
Correct option: (a)

Solution 17
Correct option: (d)
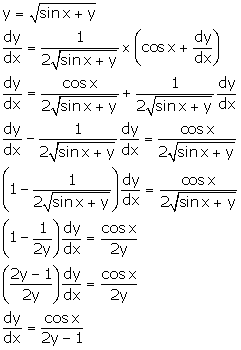
Solution 18
Correct option: (a)

Solution 19
Correct option: (b)

Solution 20
Correct option: (a)

Solution 21
Correct option: (b)

Solution 22
Correct option: (c)

Solution 23
Correct option:(d)

Solution 24
Correct option: (a)

Solution 25
Correct option: (b)
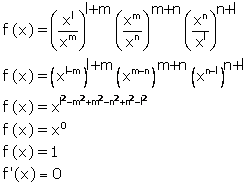
Solution 26
Correct option: (c)
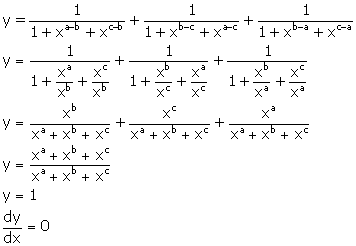
Solution 27
Correct option:(a)

Solution 28
Correct option: (b)
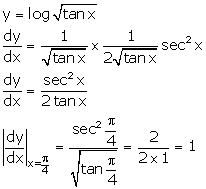
Solution 29
Correct option: (b)

Solution 30
Correct option: (a)

Solution 31
Correct option: (b)

Solution 32
Correct option: (c)
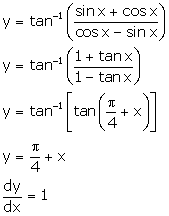
Solution 33
Given: ![]()
![]()
Differentiating w.r.t x, we get

Differentiation Exercise Ex. 11VSAQ
Solution 1

Solution 2
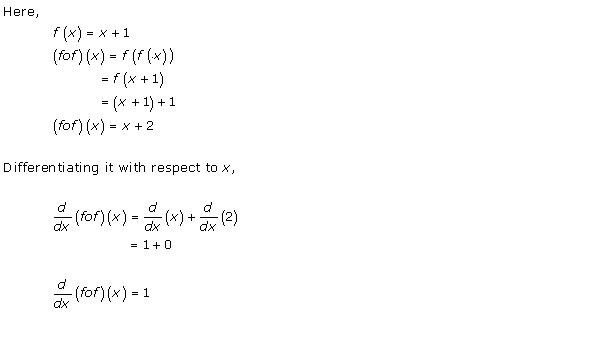
Solution 3

Solution 4

Solution 5

Solution 6
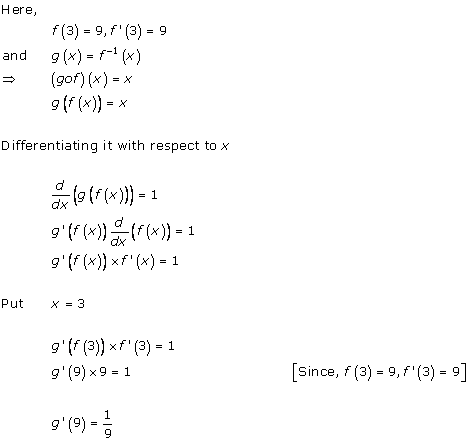
Solution 7

Solution 8

Solution 9
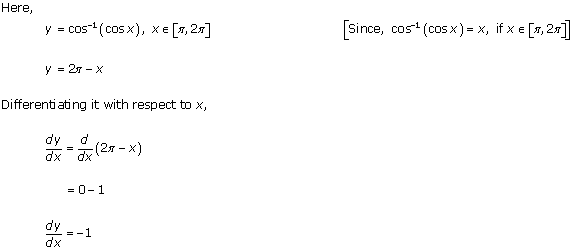
Solution 10

Solution 11
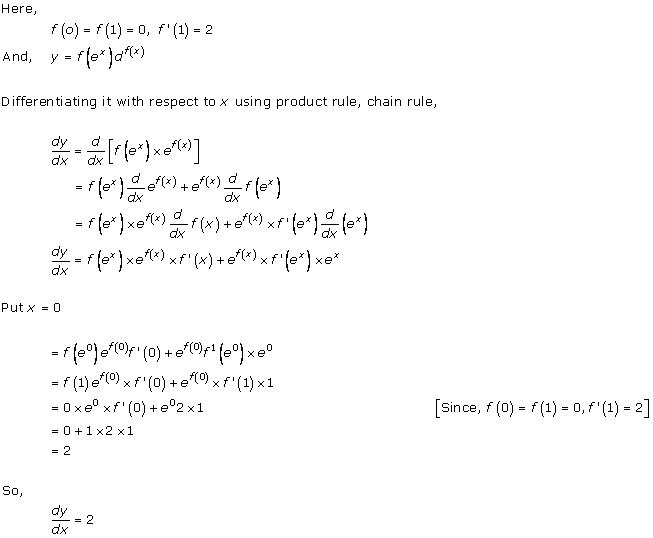
Solution 12

Solution 13
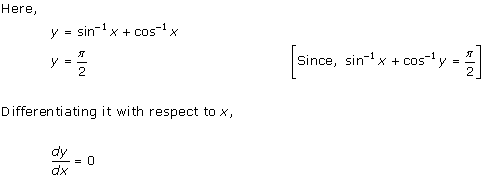
Solution 14

Solution 15
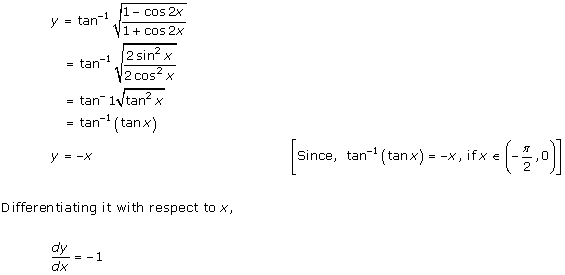
Solution 16

Solution 17

Solution 18

Solution 19

Solution 20
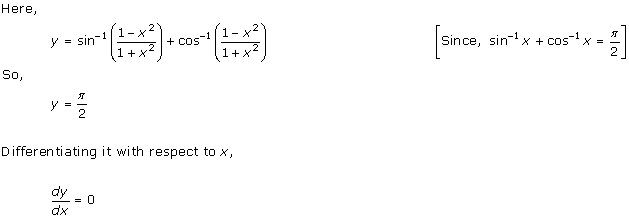
Solution 21
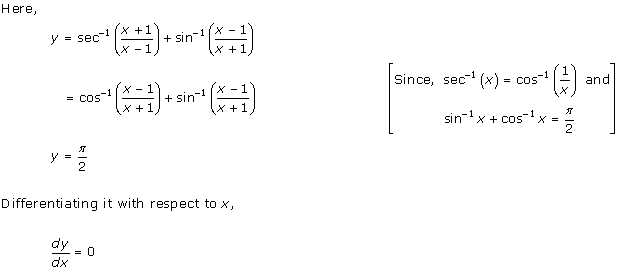
Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27
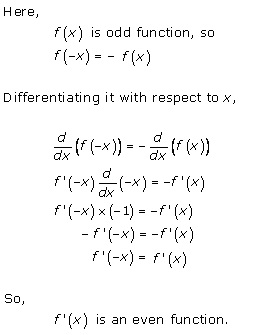
Solution 28
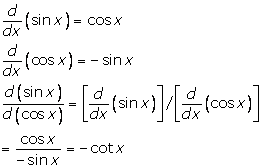
Solution 29
Given: ![]()
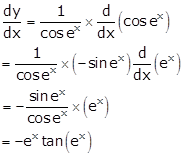
Solution 30
Given: f(x) = x + 7 and g(x) = x - 7
Now, (fog)(x) = f(g(x)) = f(x - 7) = x - 7 + 7 = x
Therefore, (fog)(x) = x
![]()