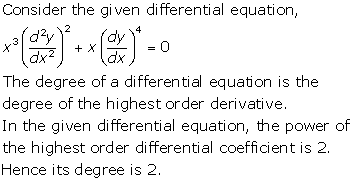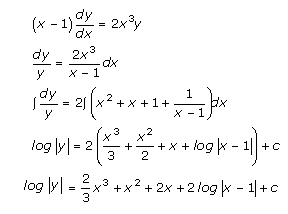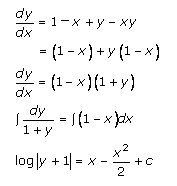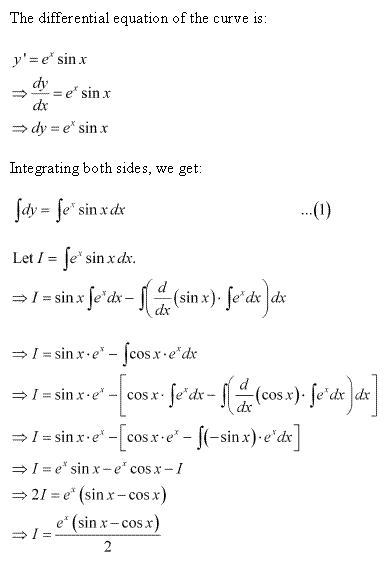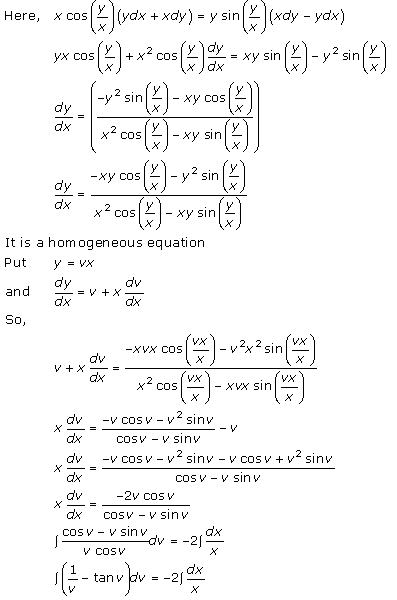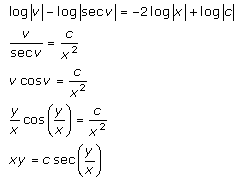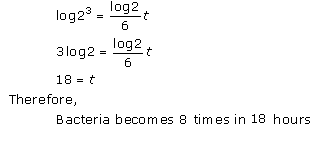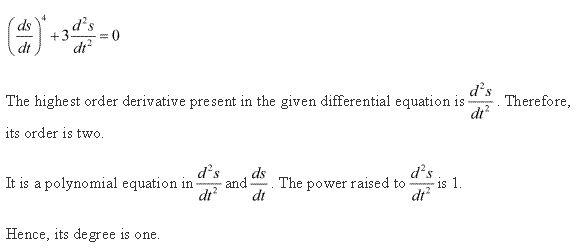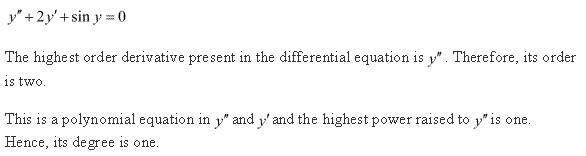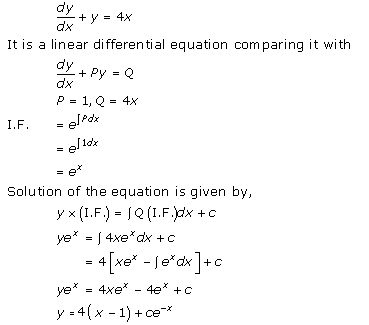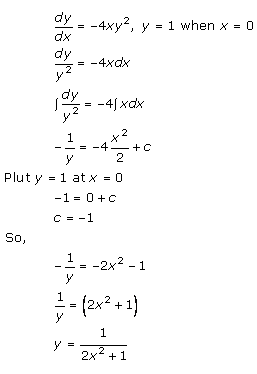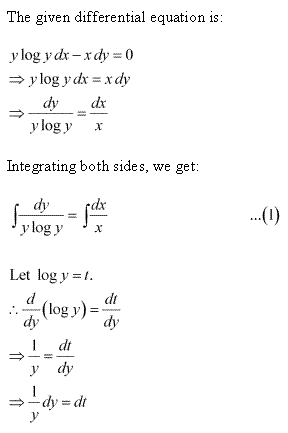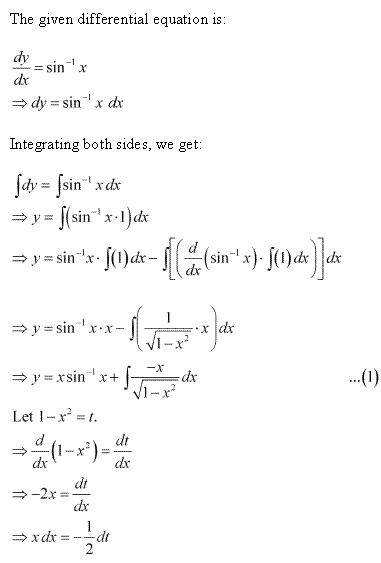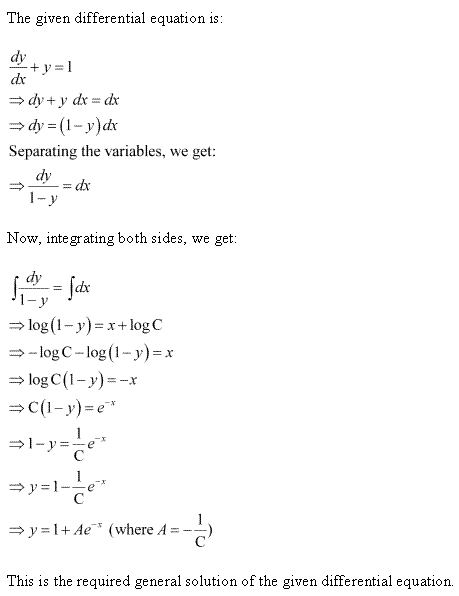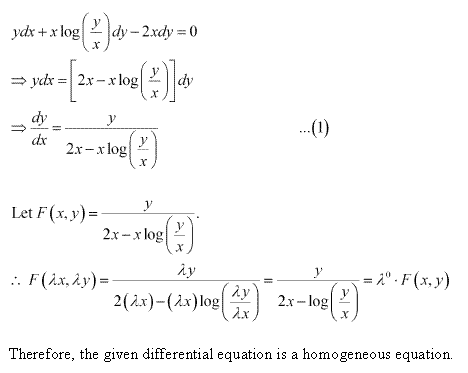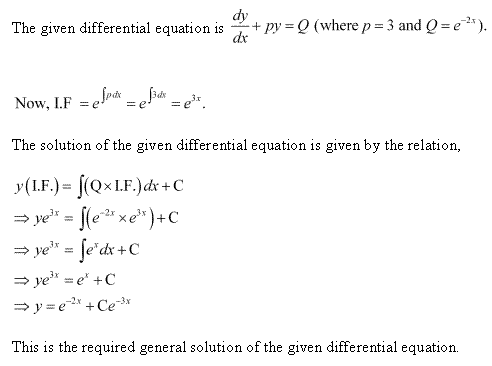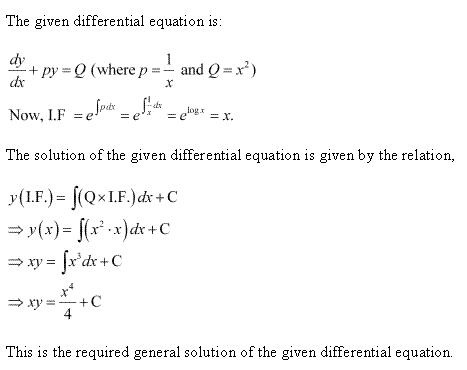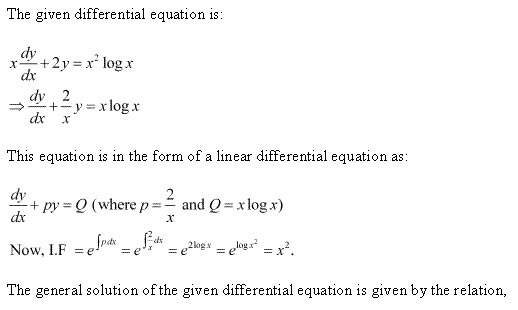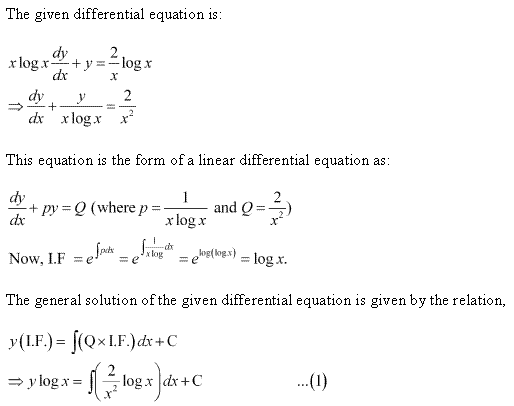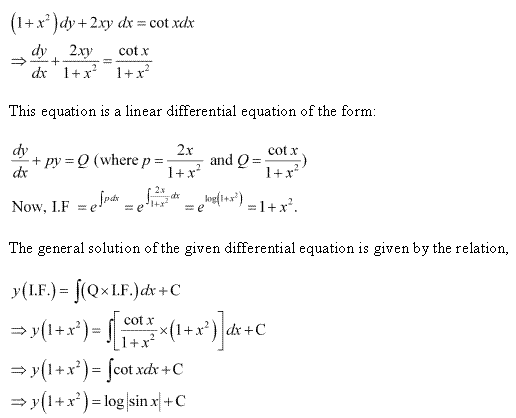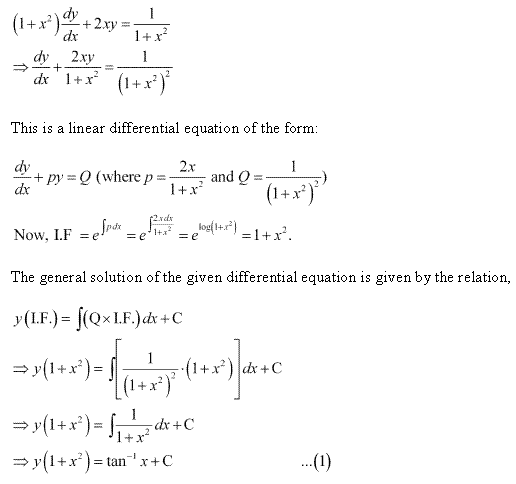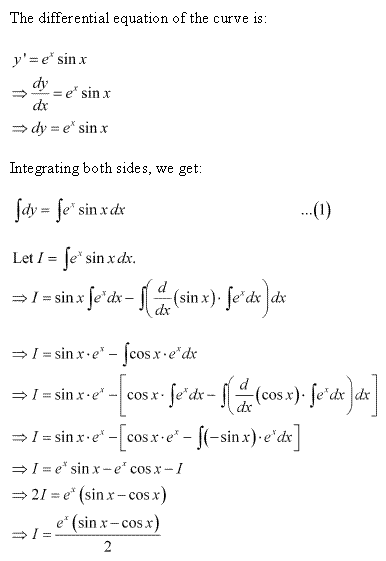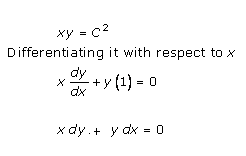Class 12-science RD SHARMA Solutions Maths Chapter 22 - Differential Equations
Differential Equations Exercise Ex. 22.1
Solution 1

Solution 2

Solution 3
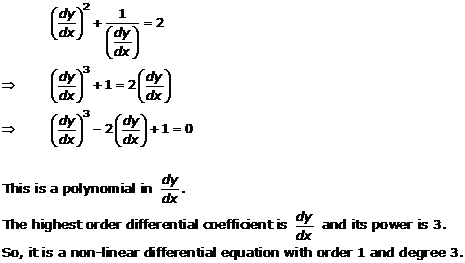
Solution 4

Solution 5

Solution 6

Solution 7
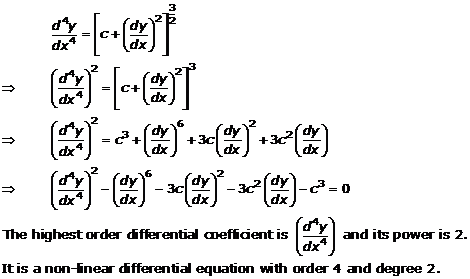
Solution 8
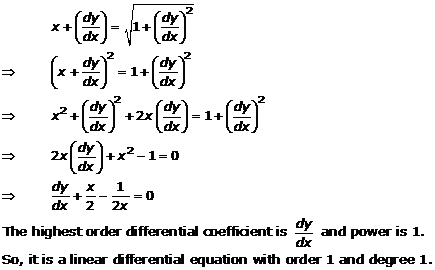
Solution 9
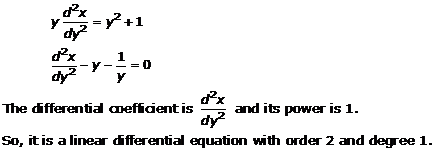
Solution 10

Solution 11

Solution 12
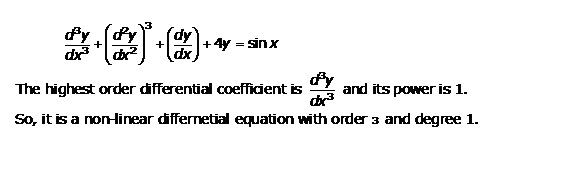
Solution 13
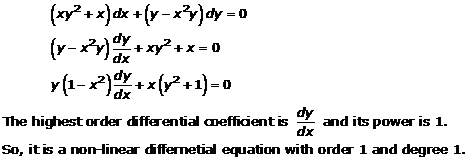
Solution 14
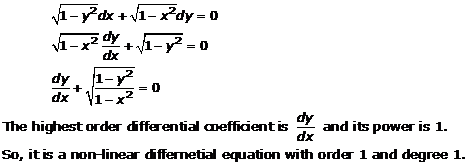
Solution 15
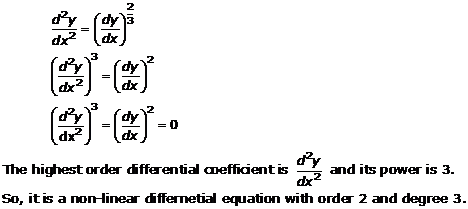
Solution 16

Solution 17
Solution 18
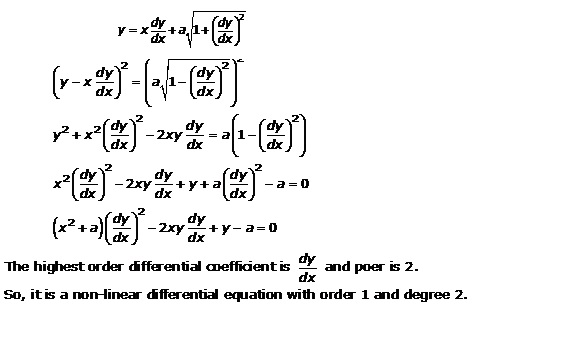
Solution 19
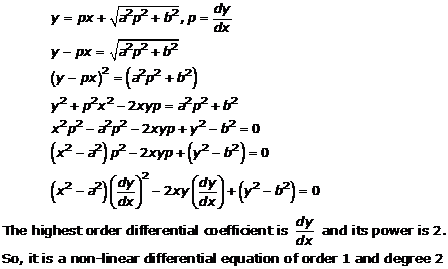
Solution 20
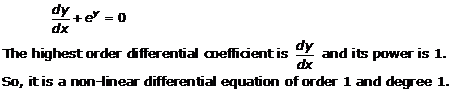
Solution 22
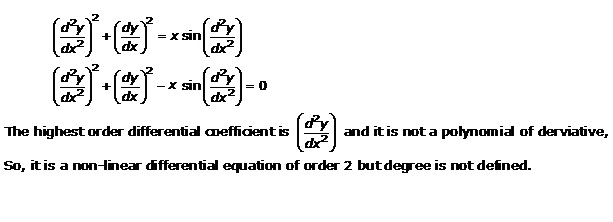
Solution 23
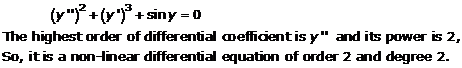
Solution 24

Solution 25
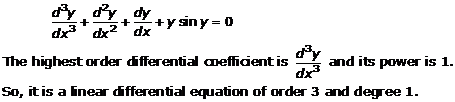
Solution 26
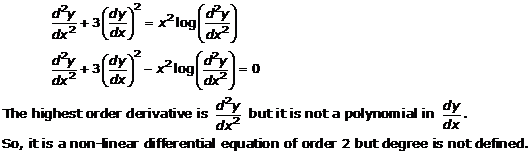
Solution 27
The order of a differential equation is the order of the highest order derivative appearing in the equation.
The degree of a differential equation is the degree of the highest order derivative.
Consider the given differential equation
![]()
In the above equation, the order of the highest order derivative is 1.
So the differential equation is of order 1.
In the above differential equation, the power of the highest order derivative is 3.
Hence, it is a differential equation of degree 3.
Since the degree of the above differential equation is 3, more than one, it is a non-linear differential equation.
Differential Equations Exercise Ex. 22.2
Solution 1
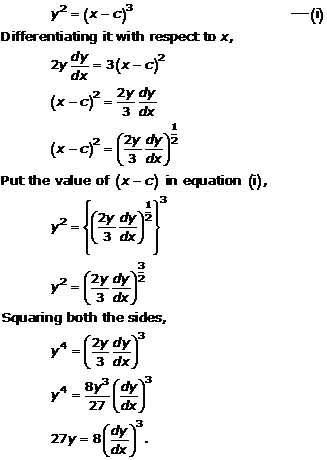
Solution 2
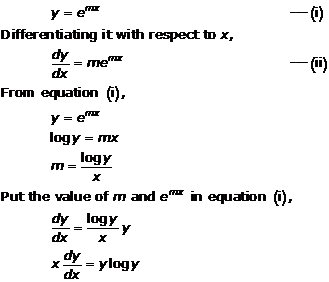
Solution 3(i)

Solution 3(ii)
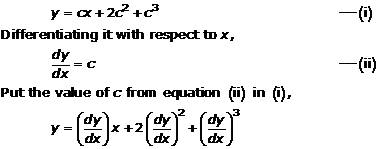
Solution 3(iii)

Solution 3(iv)

Solution 4
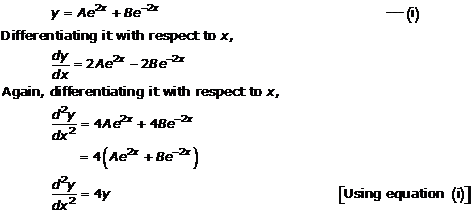
Solution 5
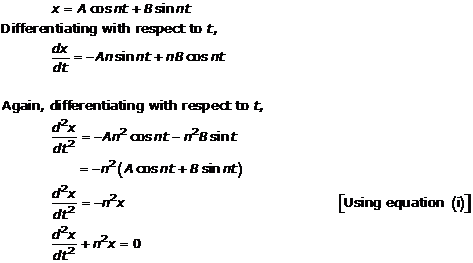
Solution 6
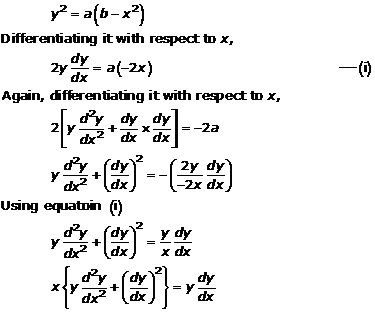
Solution 7
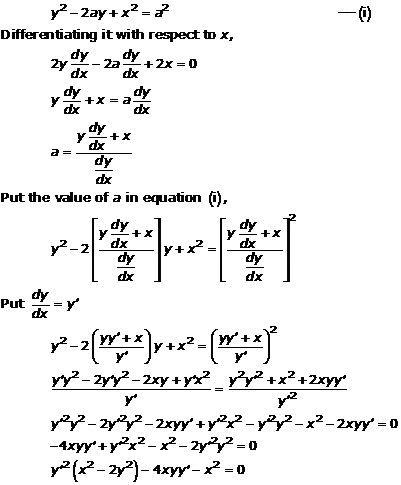
Solution 8
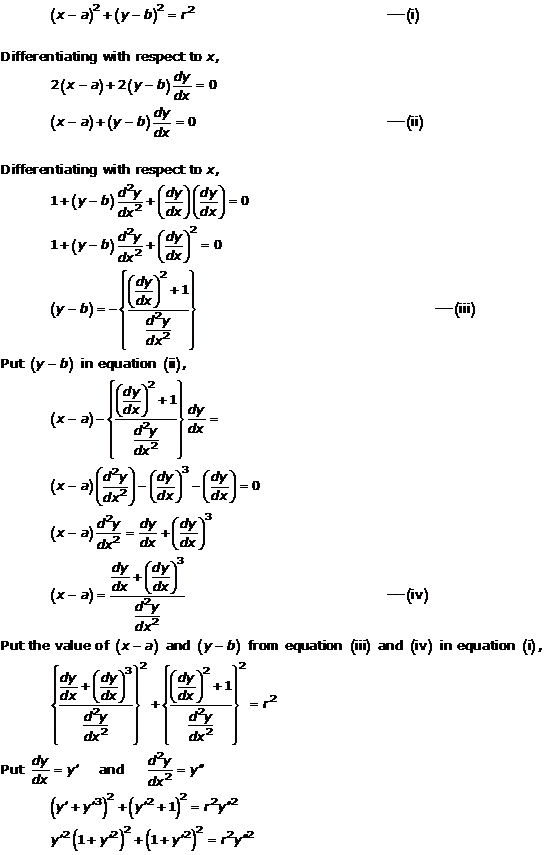
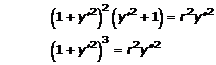
Solution 9

Solution 10
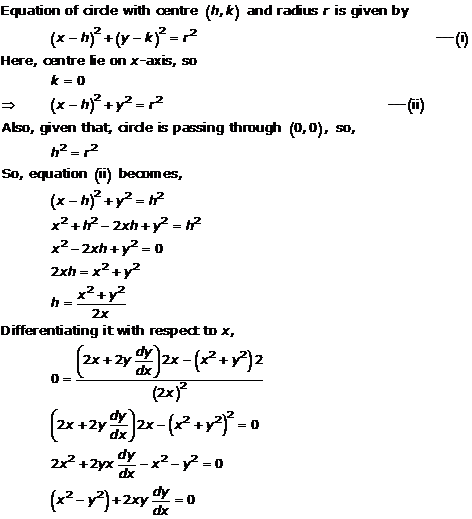
Solution 11
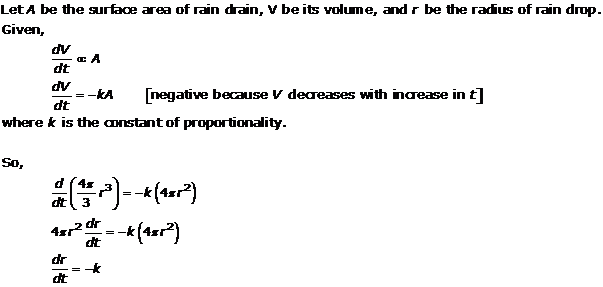
Solution 12

Solution 13
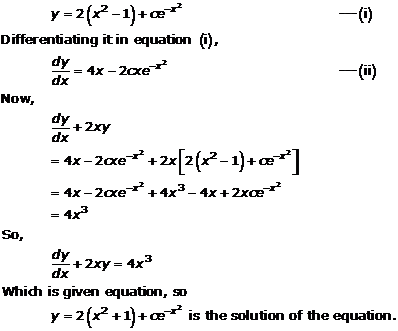
Solution 14
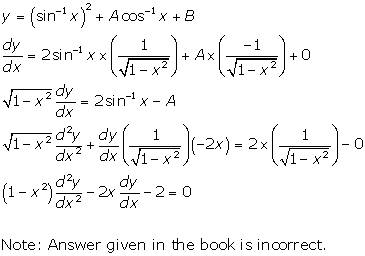
Solution 15(i)

Solution 15(ii)
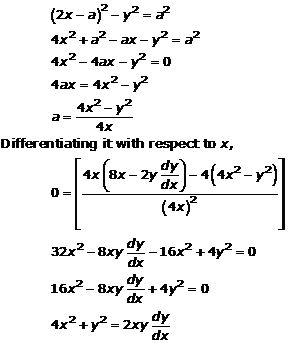
Solution 15(iii)

Solution 16(i)
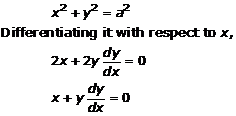
Solution 16(ii)
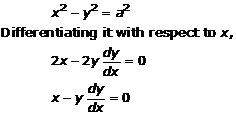
Solution 16(iii)
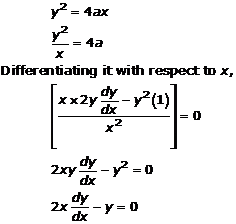
Solution 16(iv)

Solution 16(v)
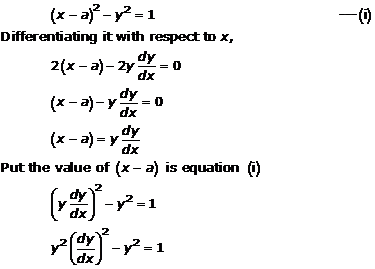
Solution 16(vi)
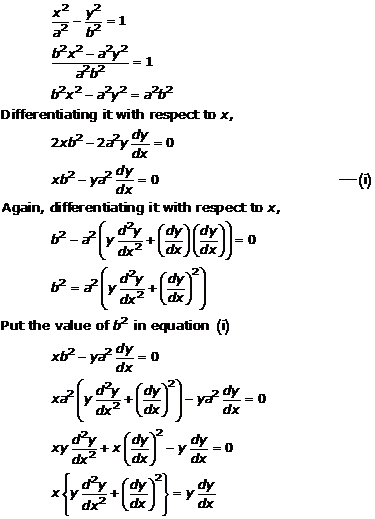
Solution 16(vii)
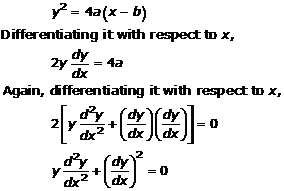
Solution 16(viii)

Solution 16(ix)
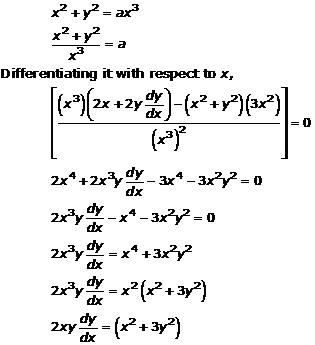
Solution 16(x)
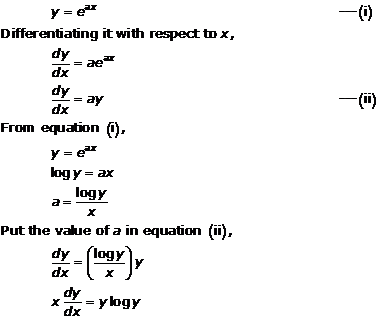
Solution 17

Solution 18

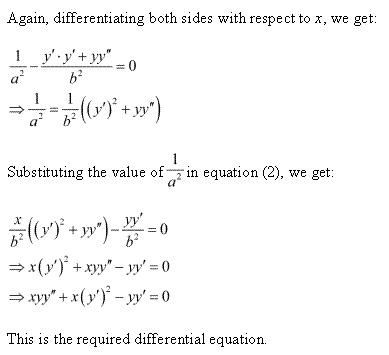
Solution 19

Differential Equations Exercise Ex. 22.3
Solution 1
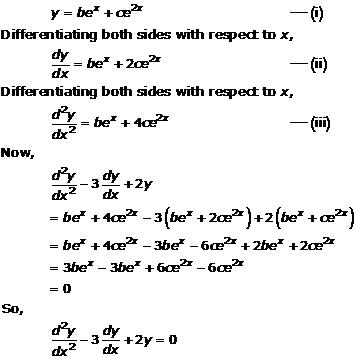
Solution 2
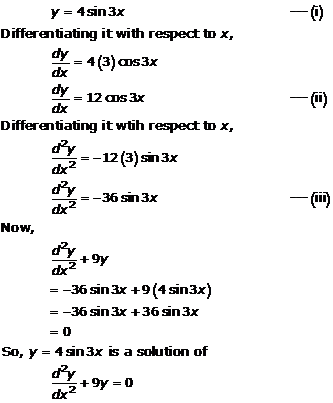
Solution 3

Solution 4
Solution 5
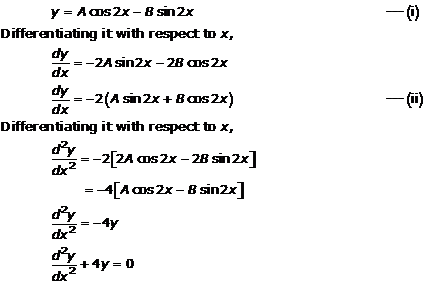
Solution 6
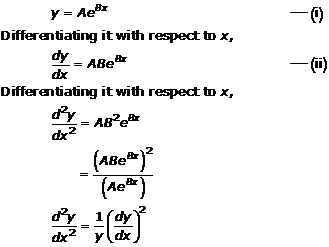
Solution 7

Solution 8
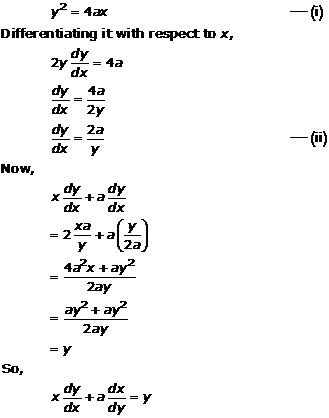
Solution 9

Solution 10
Solution 11
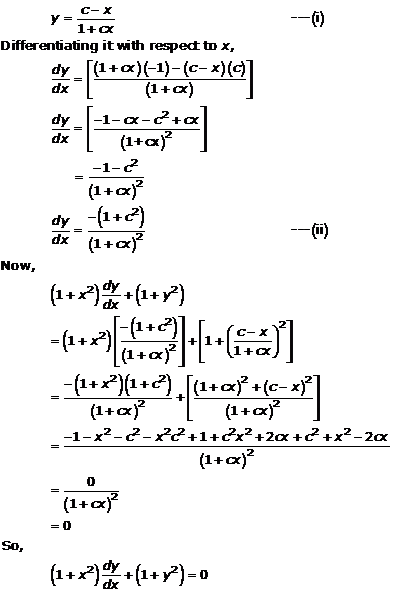
Solution 12
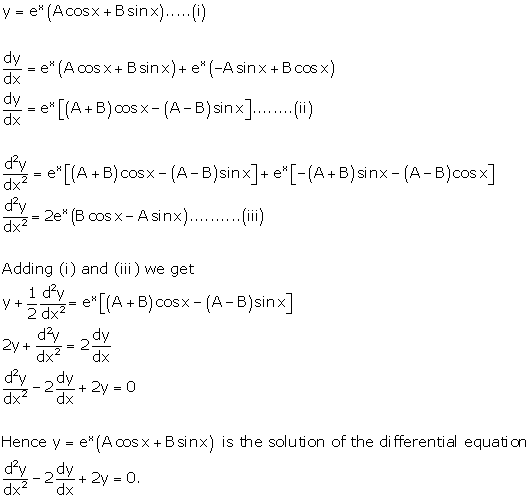
Solution 13
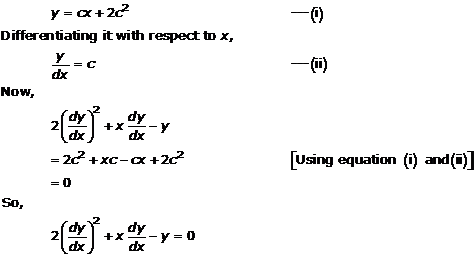
Solution 14

Solution 15
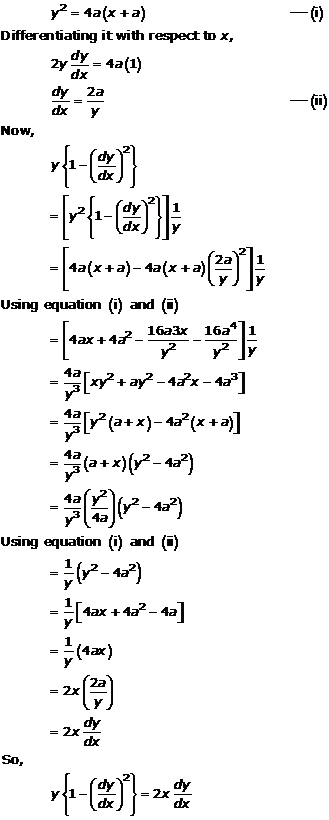
Solution 16
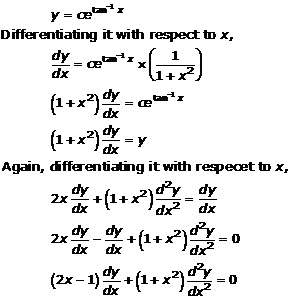
Solution 17

Solution 18

Solution 19
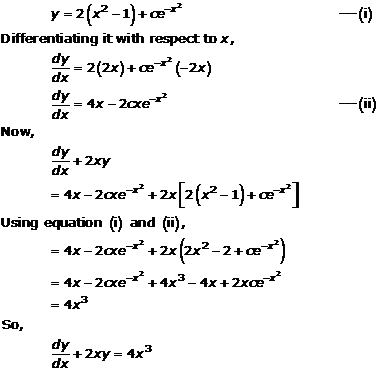
Solution 20

Solution 21(i)

Solution 21(ii)
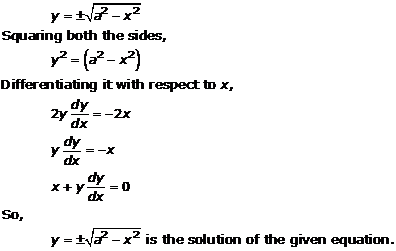
Solution 21(iii)
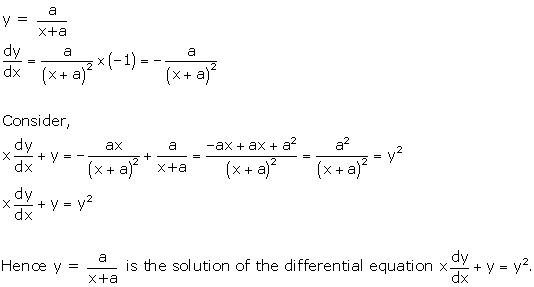
Solution 21(iv)
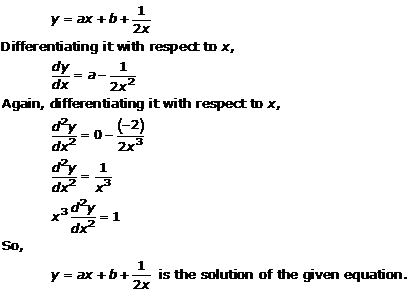
Solution 21(v)
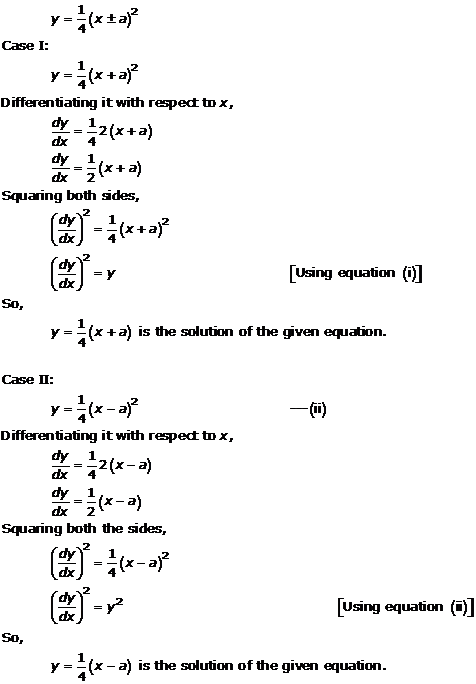
Differential Equations Exercise Ex. 22.4
Solution 1
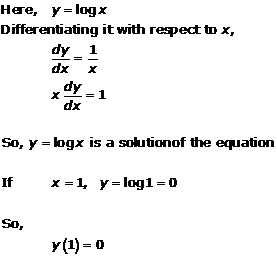
Solution 2

Solution 3

Solution 4
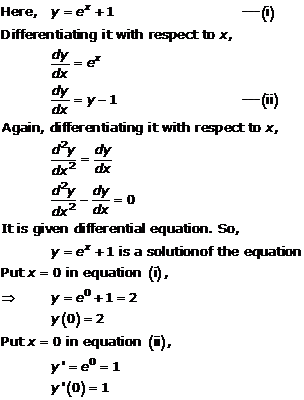
Solution 5
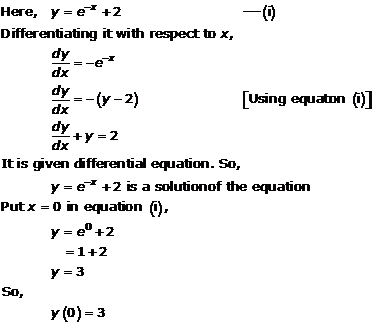
Solution 6
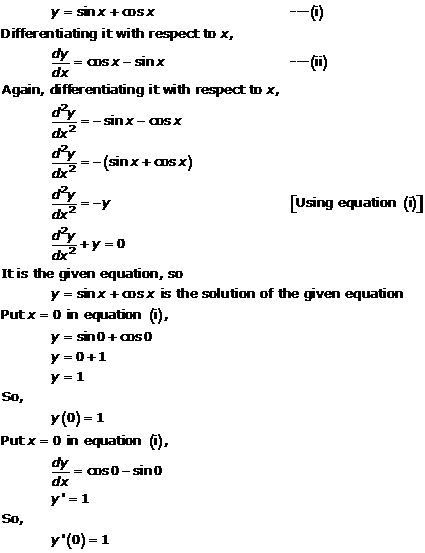
Solution 7
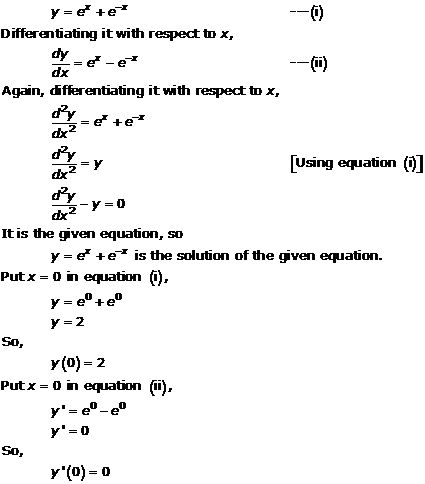
Solution 8
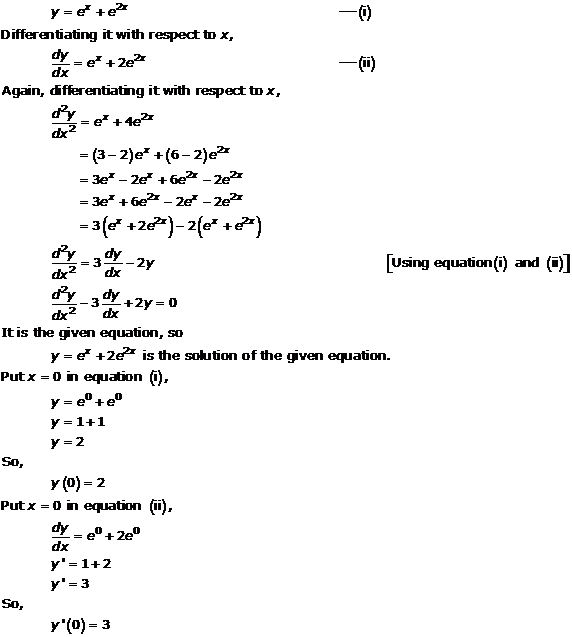
Solution 9
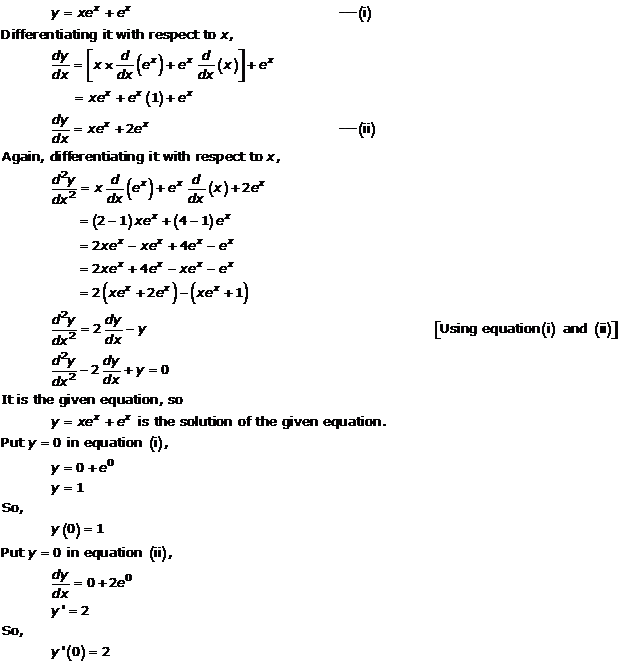
Differential Equations Exercise Ex. 22.5
Solution 1
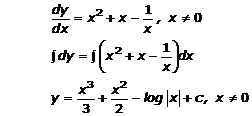
Solution 2
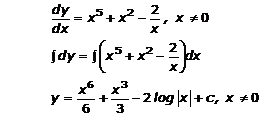
Solution 3

Solution 4
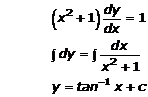
Solution 5
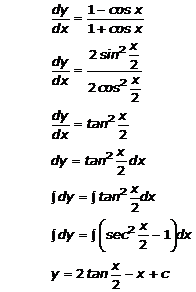
![]()
Solution 6

Solution 7
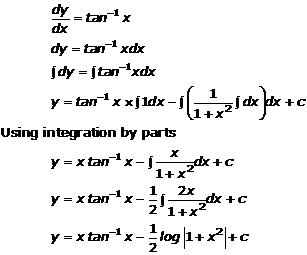
![]()
Solution 8

Solution 9
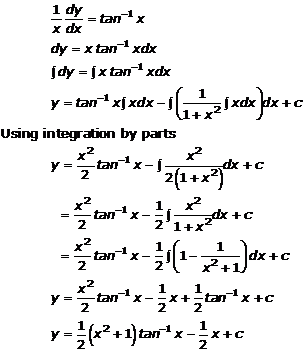
Solution 10

Solution 11
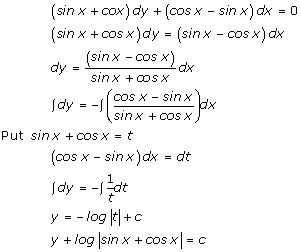
Solution 12
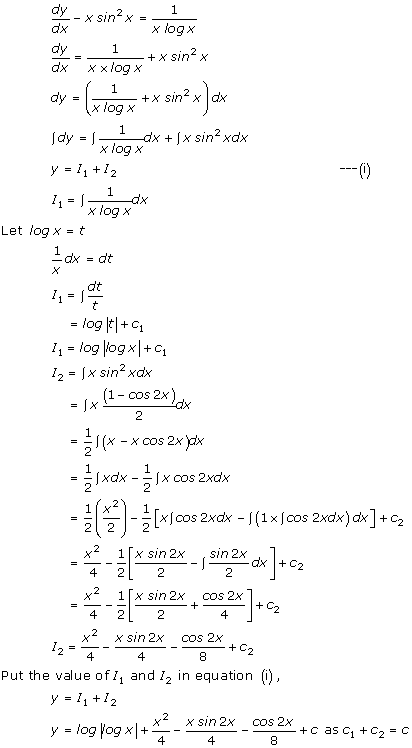
Solution 13

Solution 14
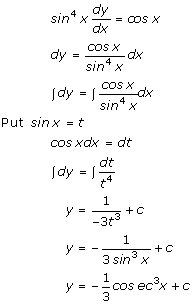
Solution 15

Solution 16
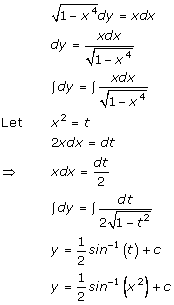
Solution 17

Solution 18

Solution 19
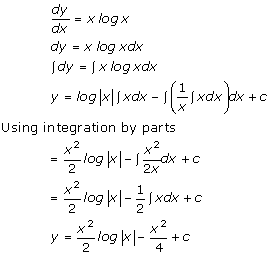
Solution 20

Solution 21

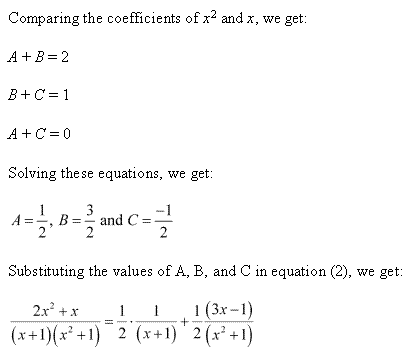

Solution 22
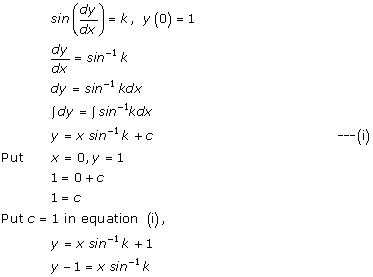
Solution 23
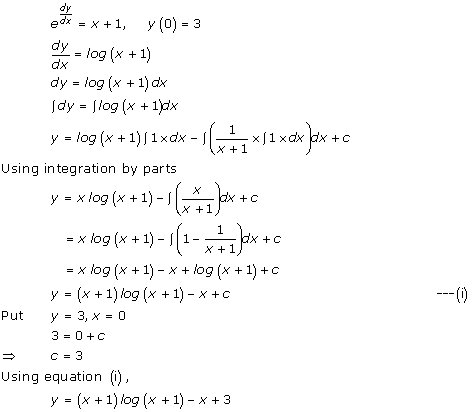
Solution 24
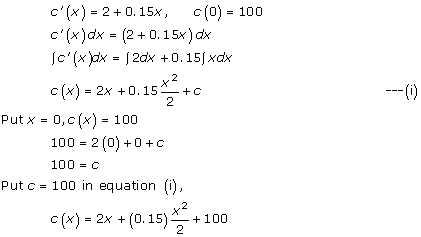
Solution 25
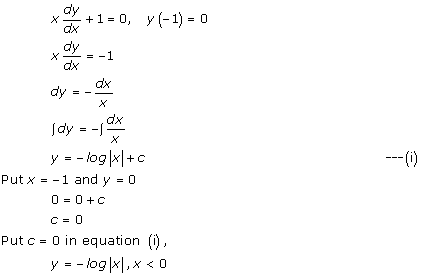
Solution 26

Differential Equations Exercise Ex. 22.6
Solution 1
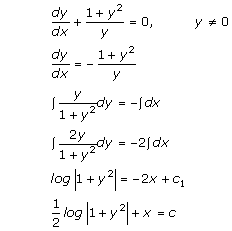
Solution 2
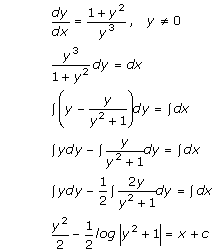
Solution 3
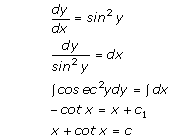
Solution 4

Differential Equations Exercise Ex. 22.7
Solution 1

Solution 2

Solution 3

Solution 4
Solution 5

Solution 6
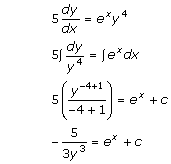
Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12
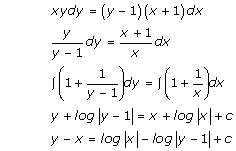
Solution 13
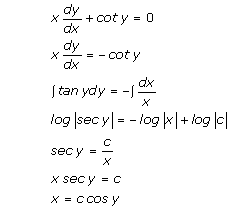
Solution 14
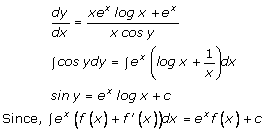
Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20

Solution 21

Solution 22
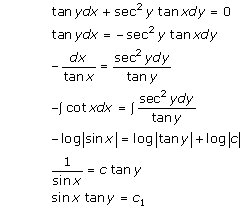
Solution 23

Solution 24
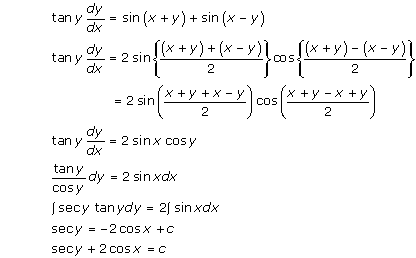
Solution 25

Solution 26

Solution 27

Solution 28

Solution 29

Solution 30
Solution 31

Solution 32
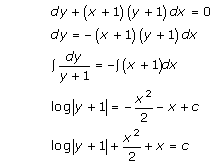
Solution 33
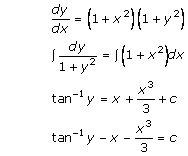
Solution 34

Solution 35

Solution 36

Solution 37(i)

Solution 37(ii)

Solution 38(i)
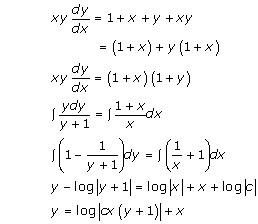
Solution 38(ii)

Solution 38(iii)
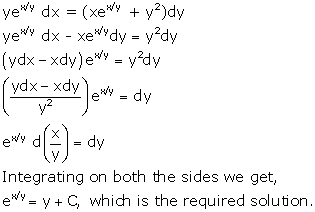
Solution 38(iv)
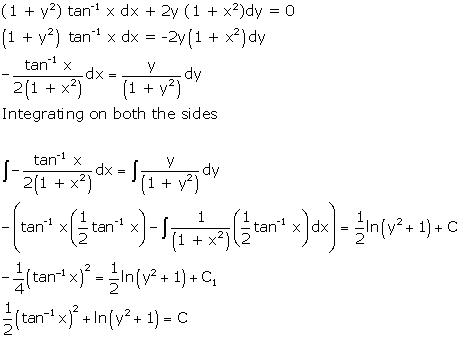
Solution 39

Solution 40

Solution 41
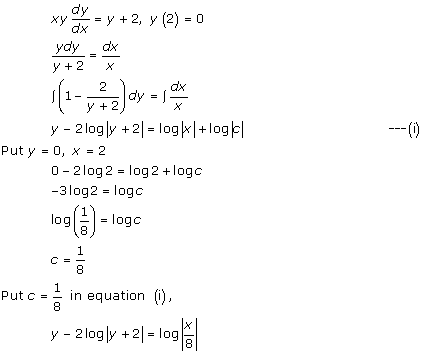
Solution 42

Solution 43

Solution 44

Solution 45(i)
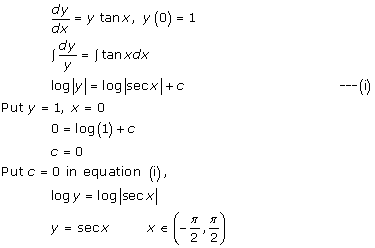
Solution 45(ii)
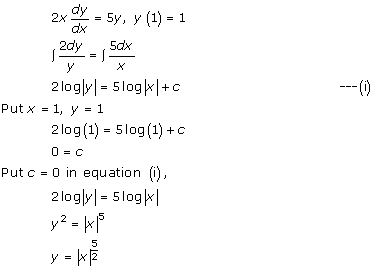
Solution 45(iii)

Solution 45(iv)

Solution 45(v)

Solution 45(vi)

Solution 45(vii)

Solution 45(viii)
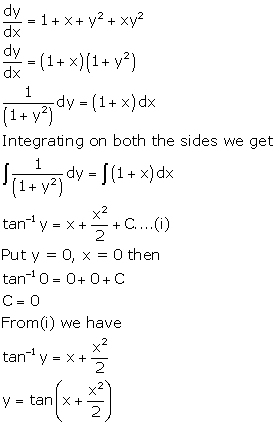
Solution 45(ix)

Solution 46

Solution 47

Solution 48
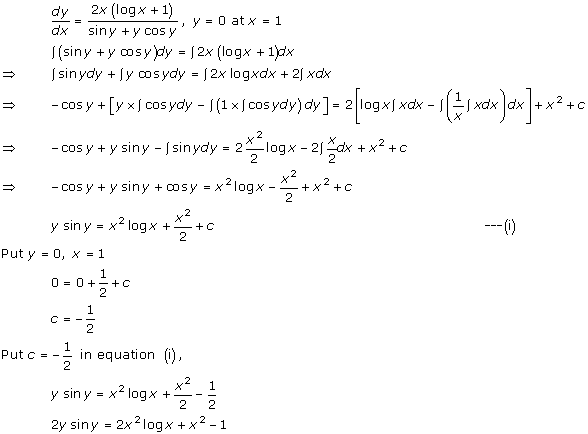
Solution 49

Solution 50

Solution 51

Solution 52
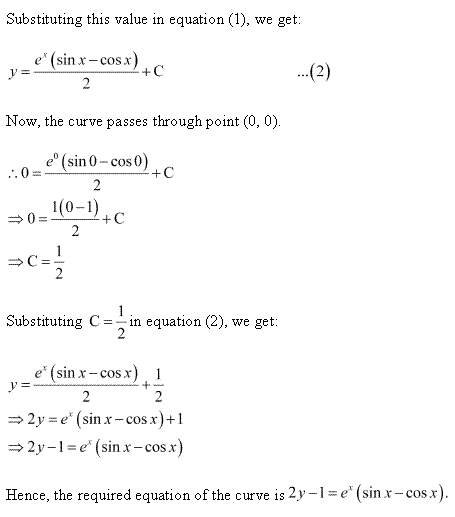
Solution 53
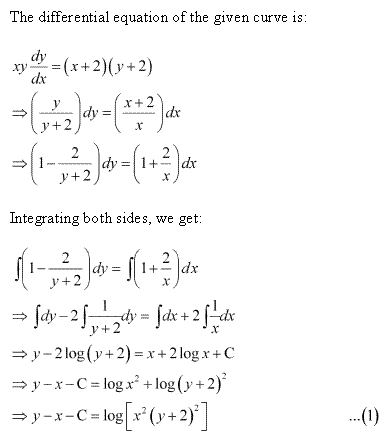
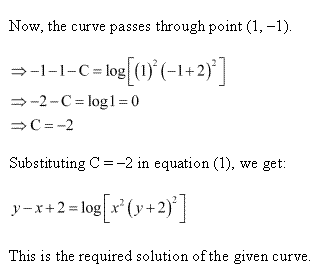
Solution 54


Solution 55
Let p, t and represent the principal, time, and rate of interest respectively.
It is given that the principal increases continuously at the rate of r% per year.

Integrating both side, we get:

Solution 56
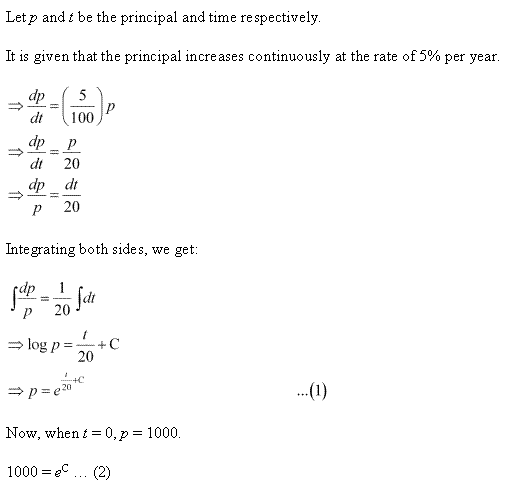
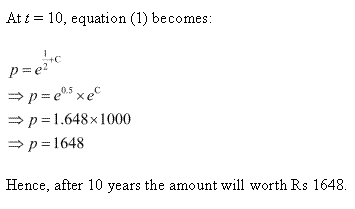
Solution 57

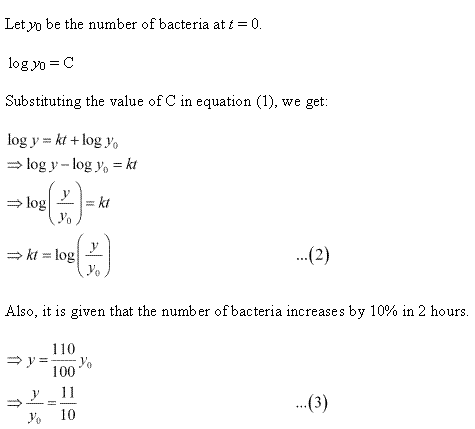
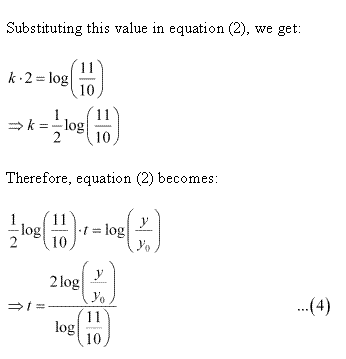 .
.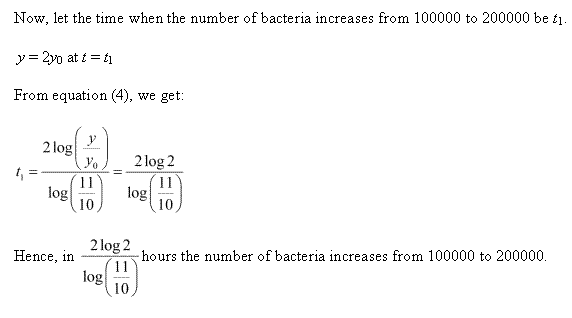
Solution 58

Differential Equations Exercise Ex. 22.8
Solution 1

Solution 2
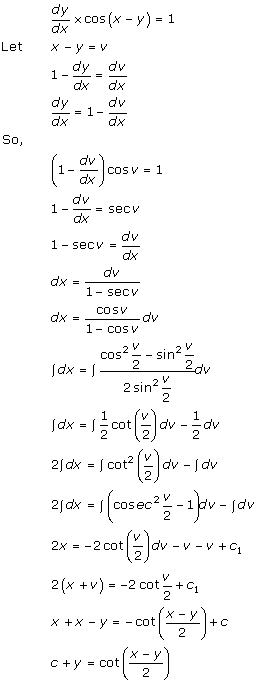
Solution 3
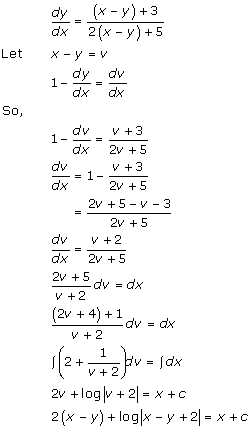
Solution 4
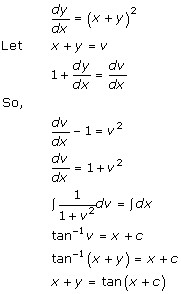
Solution 5

Solution 6
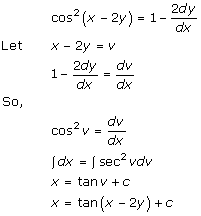
Solution 7

Solution 8

Solution 9

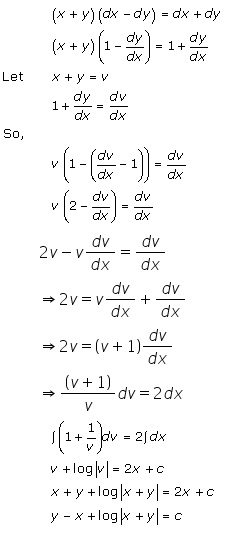
Solution 10
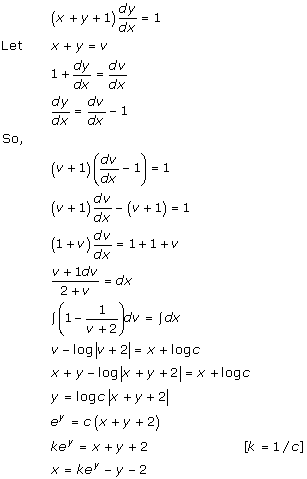
Solution 11
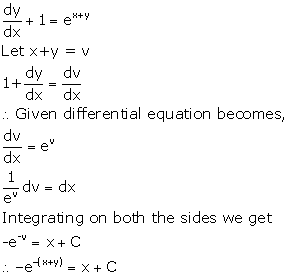
Differential Equations Exercise Ex. 22.9
Solution 1
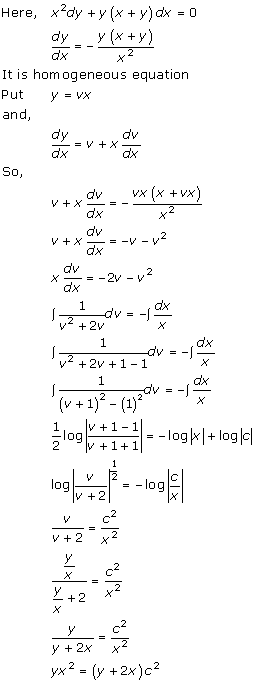
Solution 2

Solution 3

Solution 4
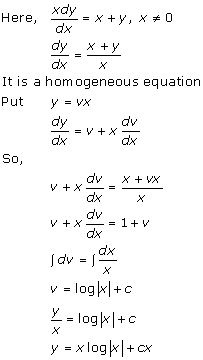
Solution 5
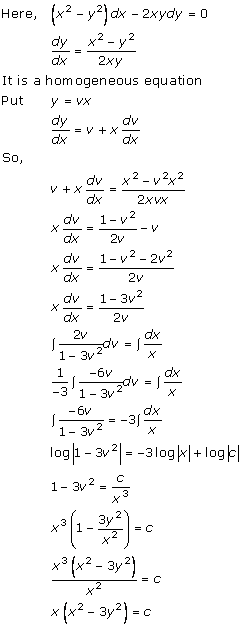
Solution 6

Solution 7

Solution 8

Solution 9
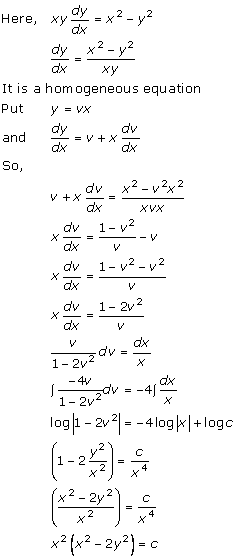
Solution 10
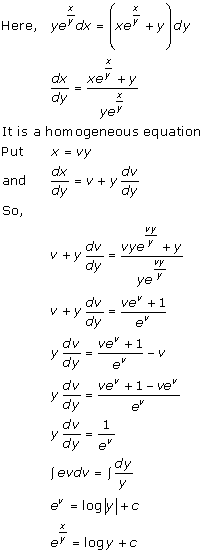
Solution 11
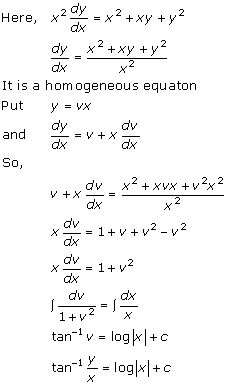
Solution 12
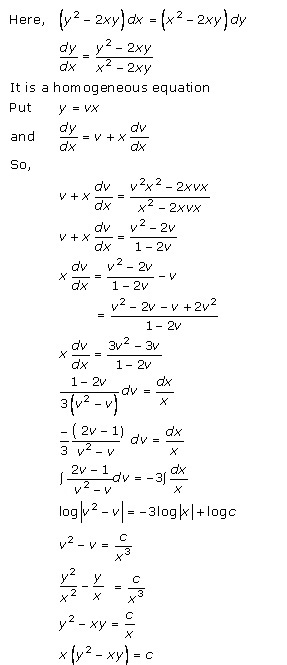
Solution 13


Solution 14

Solution 15


Solution 16

Solution 17
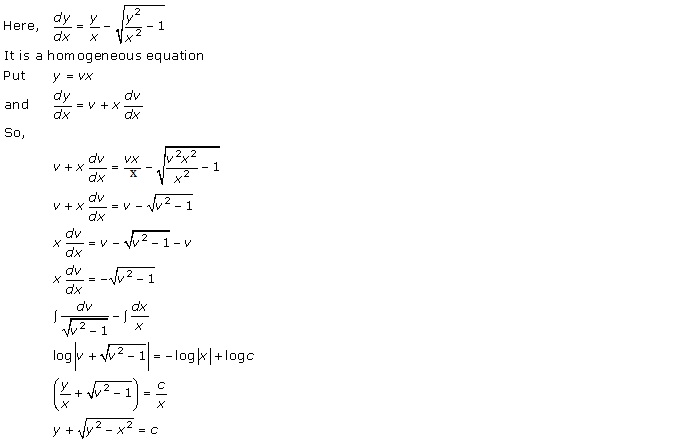
Solution 18
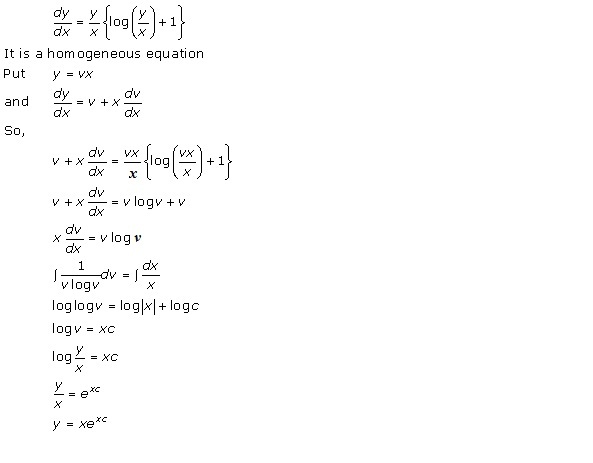
Solution 19

Solution 20

Solution 21
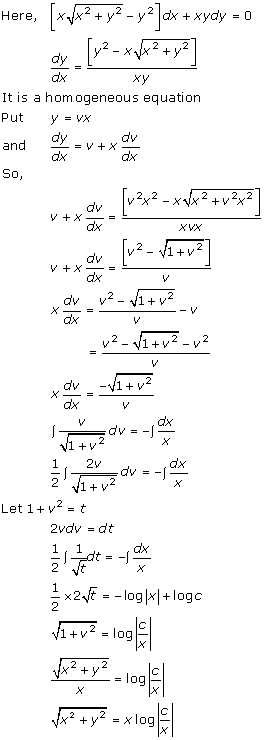
Solution 22
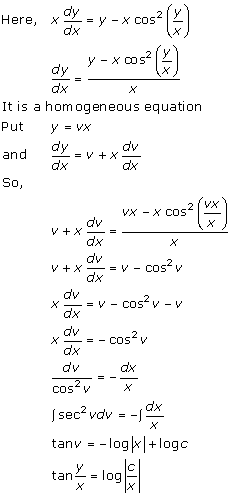
Solution 23
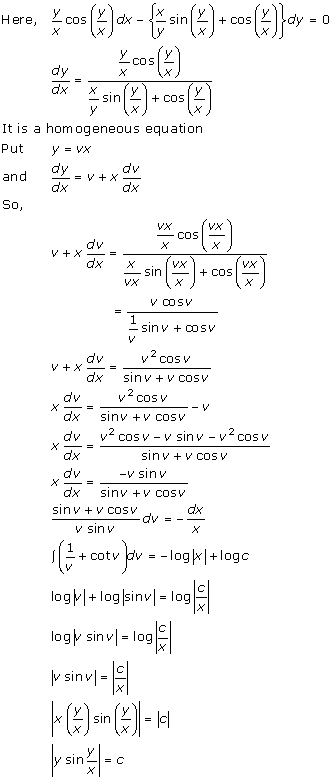
Solution 24
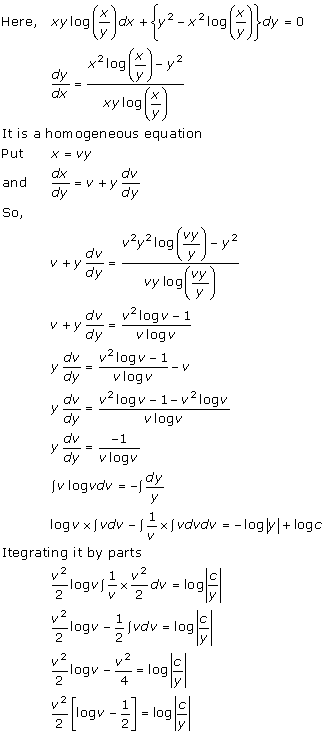
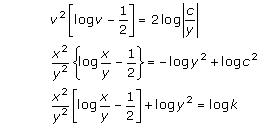
Solution 25

Solution 26

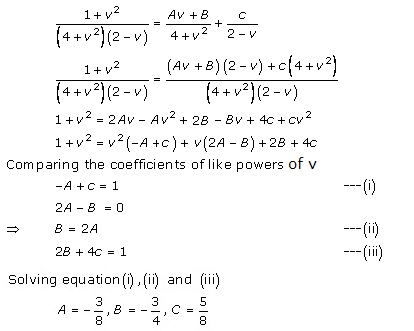
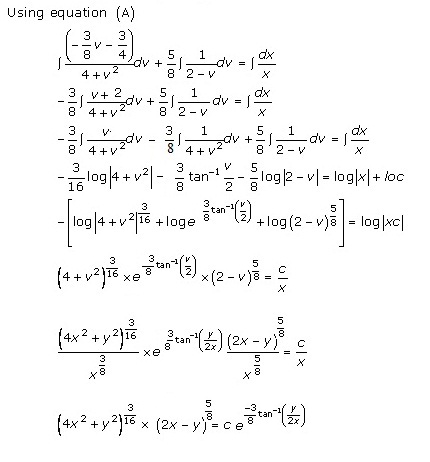
Solution 27
Solution 28
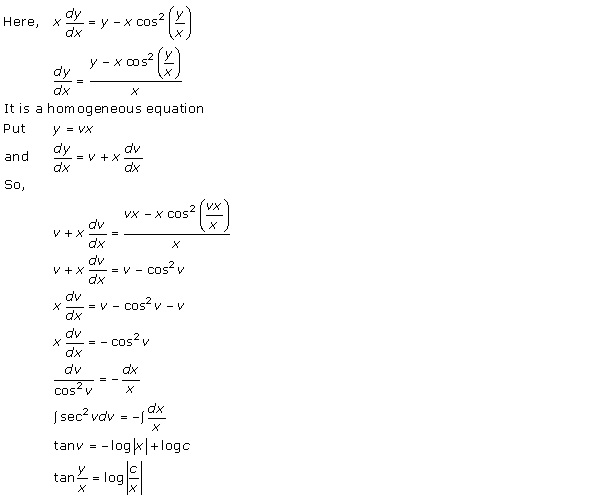
Solution 29
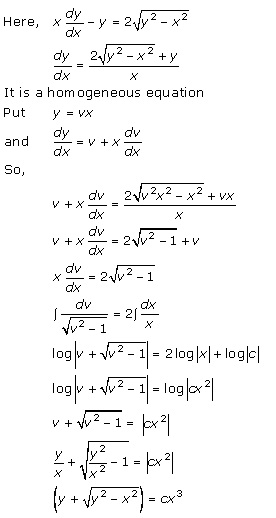
Solution 30
Solution 31
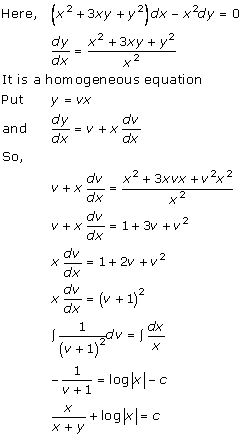
Solution 32
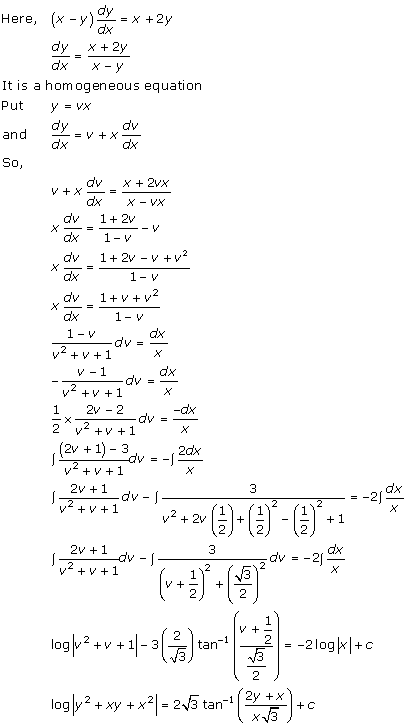
Solution 33

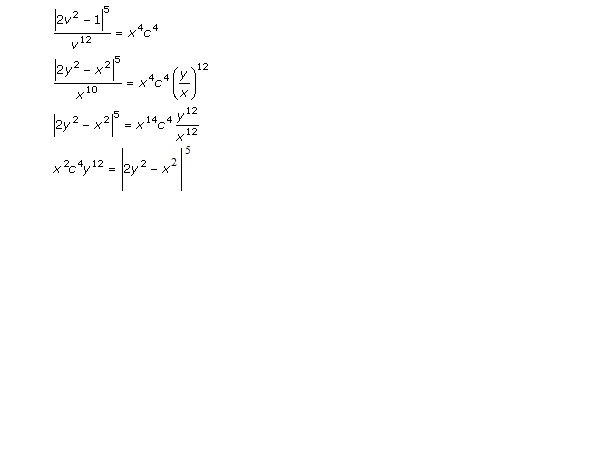
Solution 34
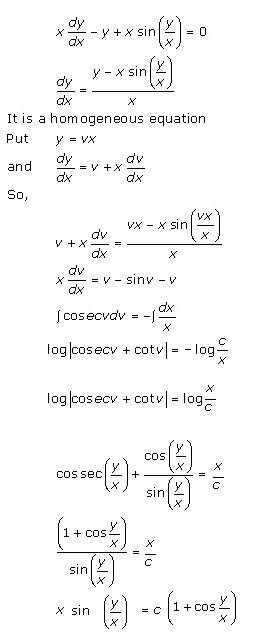
Solution 35
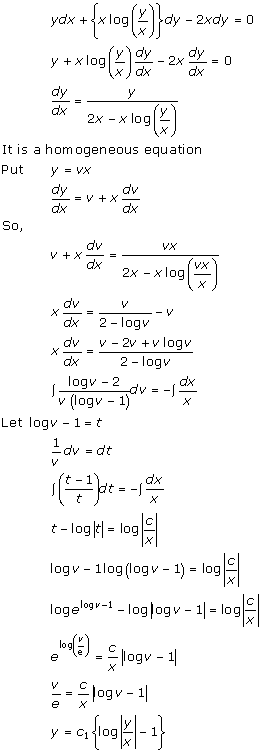
Solution 36(i)
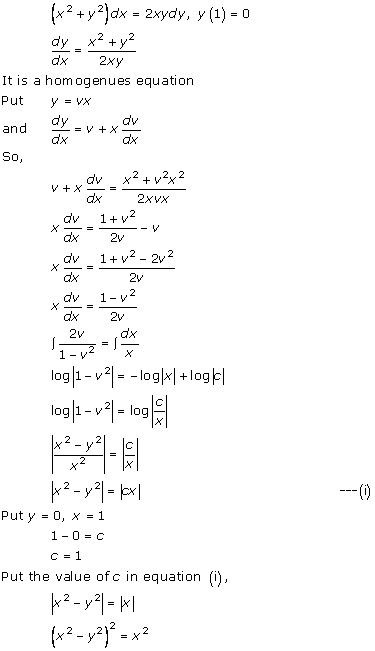
Solution 36(ii)

Solution 36(iii)

Solution 36(iv)

Solution 36(v)
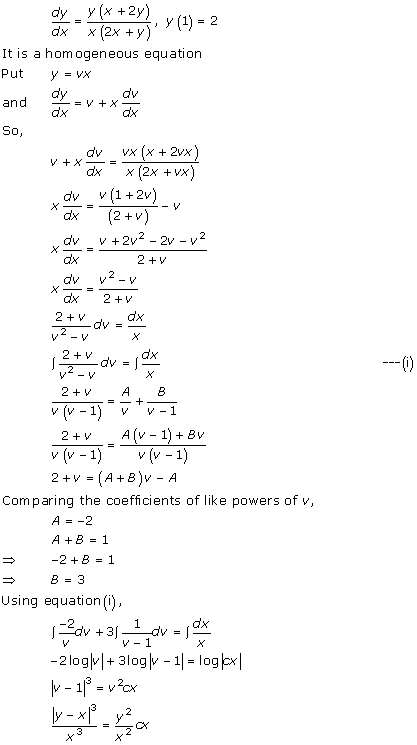
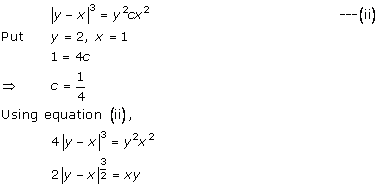
Solution 36(vi)
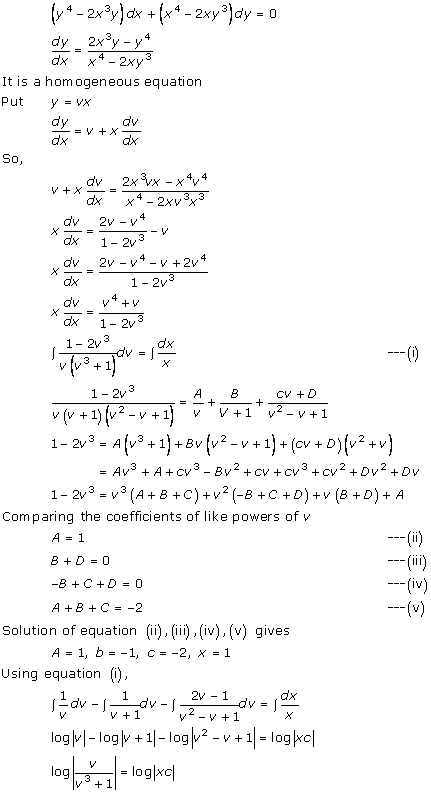

Solution 36(vii)

Solution 36(viii)
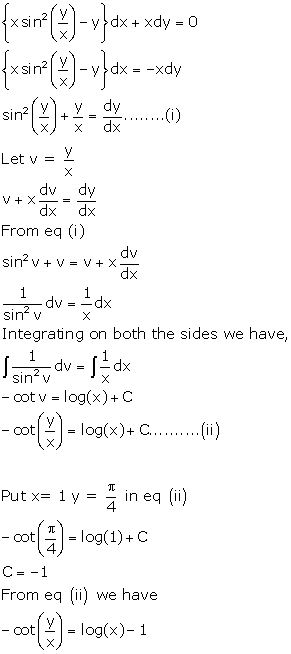
Solution 36(ix)

Solution 37

![]()
Solution 38



Solution 39

Differential Equations Exercise Ex. 22.10
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9
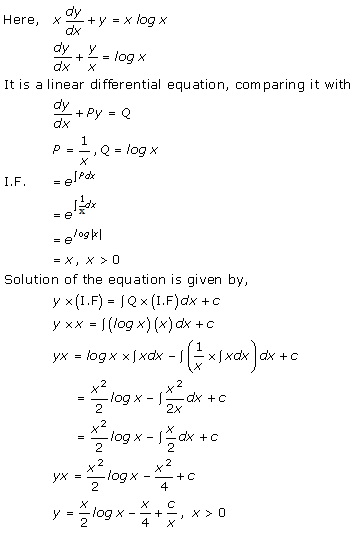
Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17
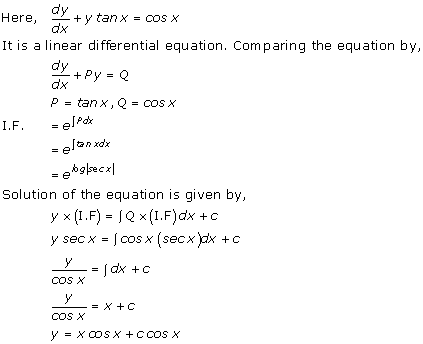
Solution 18

Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26
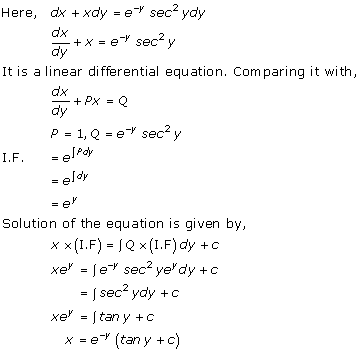
Solution 27
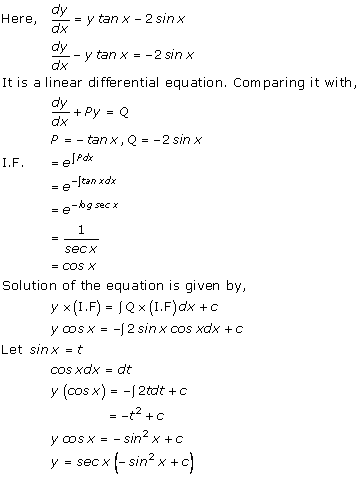
Solution 28

Solution 29

Solution 30

Solution 31

Solution 32
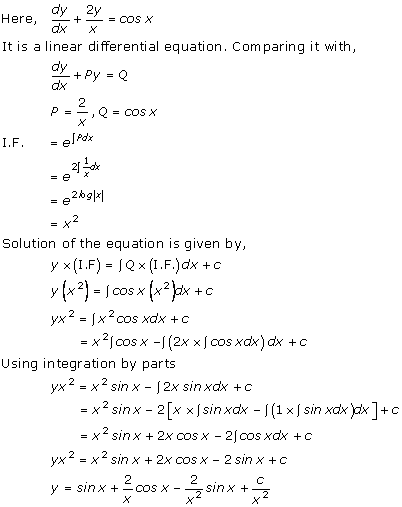
Solution 33

Solution 34

Solution 35

Solution 36(i)

Solution 36(ii)
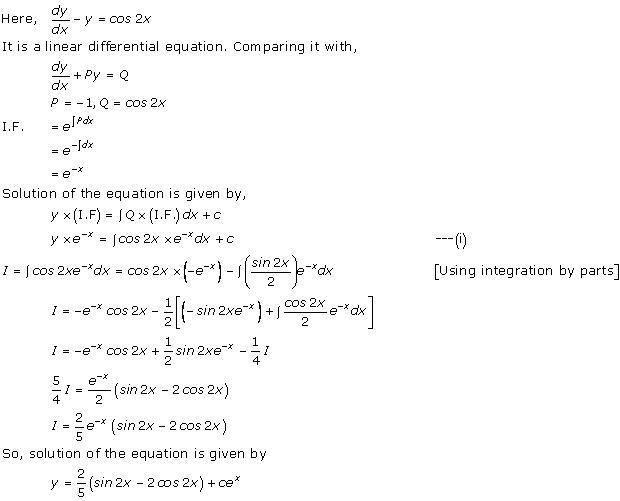
Solution 36(iii)
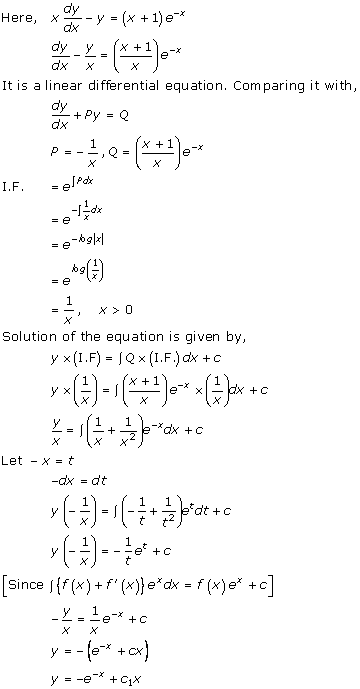
Solution 36(iv)
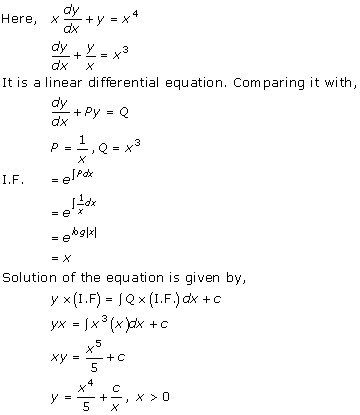
Solution 36(v)
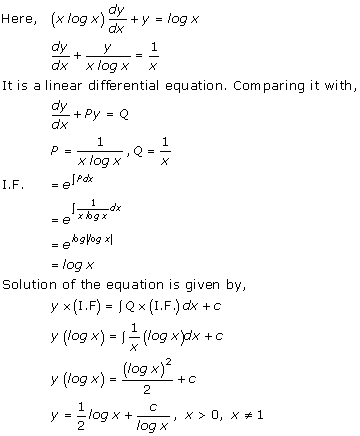
Solution 36(vi)
Solution 36(vii)
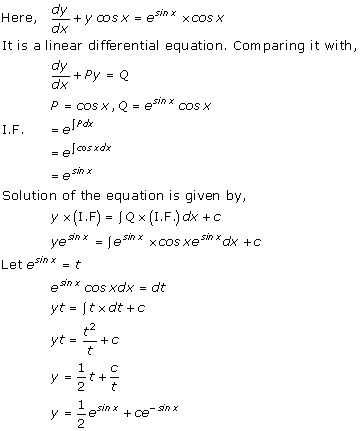
Solution 36(viii)

Solution 36(ix)

Solution 36(x)

Solution 36(xi)

Solution 36(xii)

Solution 37(i)

Solution 37(ii)

Solution 37(iii)

Solution 37(iv)

Solution 37(v)

Solution 37(vi)

Solution 37(vii)

Solution 37(viii)

Solution 37(ix)

Solution 37(x)

Solution 37(xi)

Solution 37(xii)
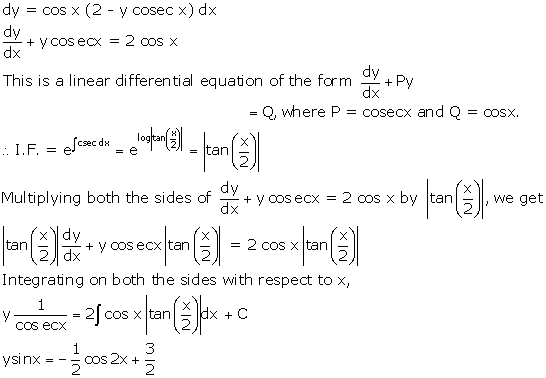
Solution 38
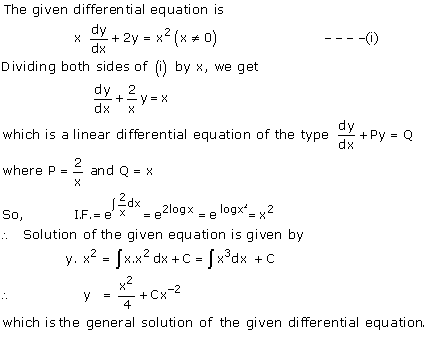
Solution 39
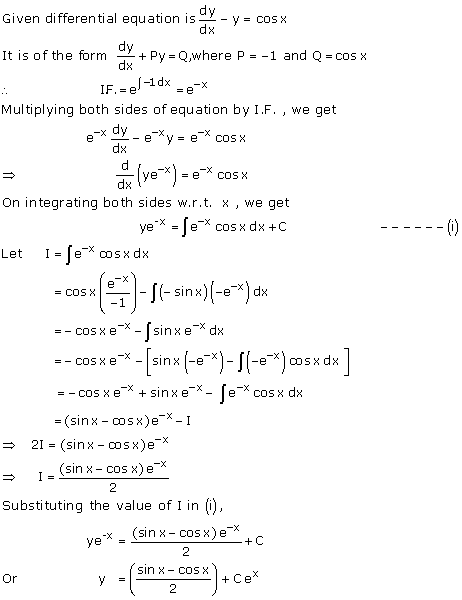
Solution 40

Solution 41
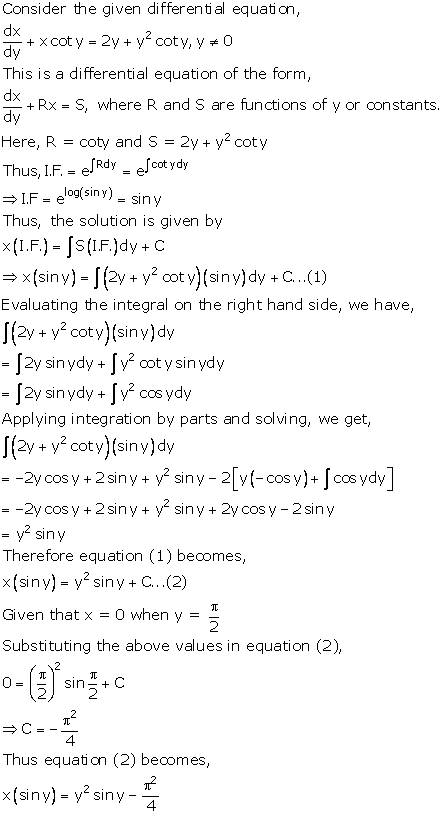
Differential Equations Exercise Ex. 22.11
Solution 1

Solution 2

Solution 3
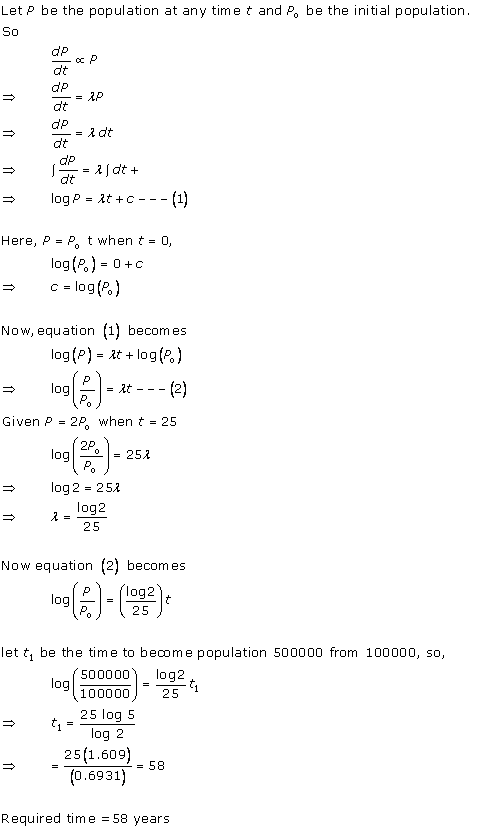
Solution 4

Solution 5

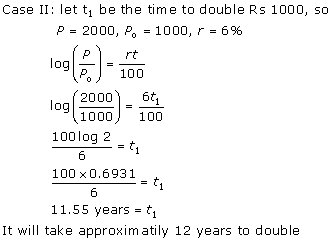
Solution 6


Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

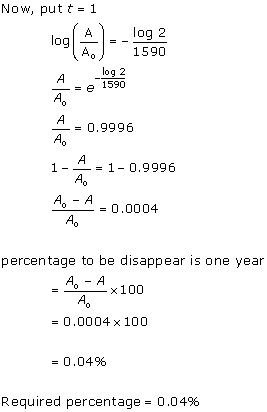
Solution 13

Solution 14

Solution 15

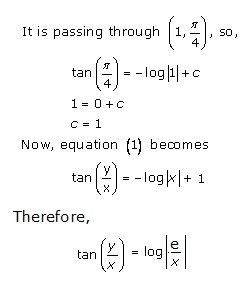
Solution 16


Solution 17

Solution 18

Solution 19

Solution 20

Solution 21

Solution 22
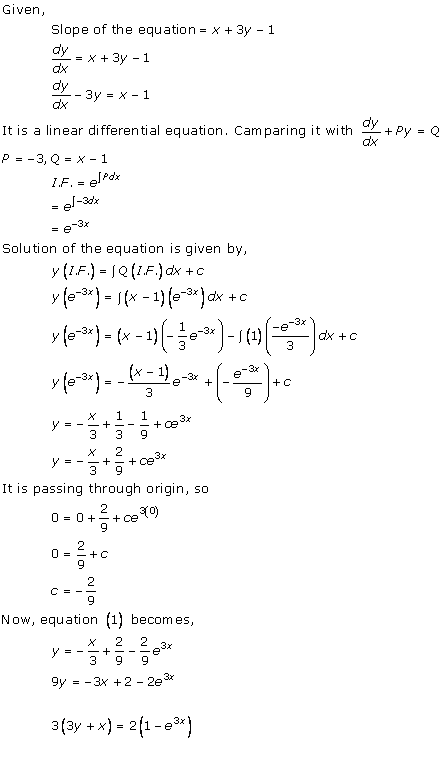
Solution 23

Solution 24
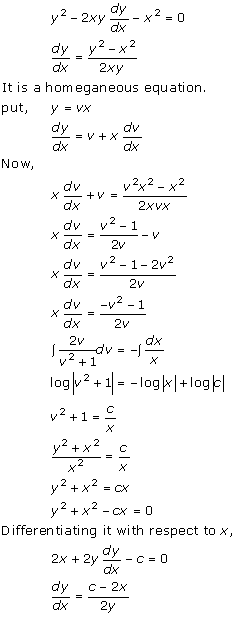

Solution 25

Solution 26

Solution 27
Solution 28

Solution 29
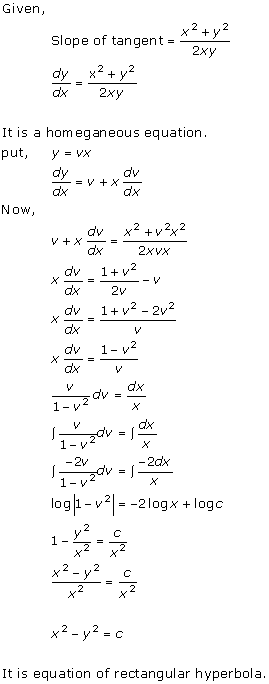
Solution 30
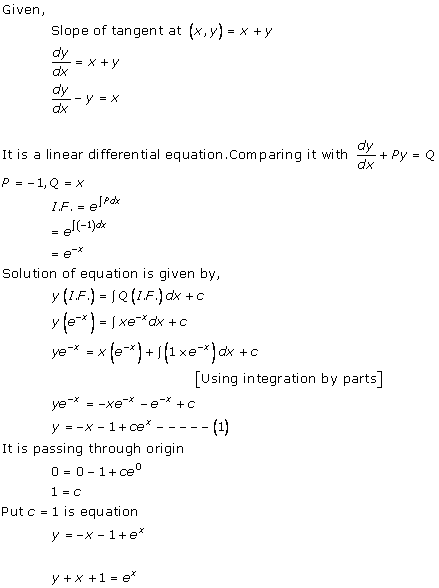
Solution 31
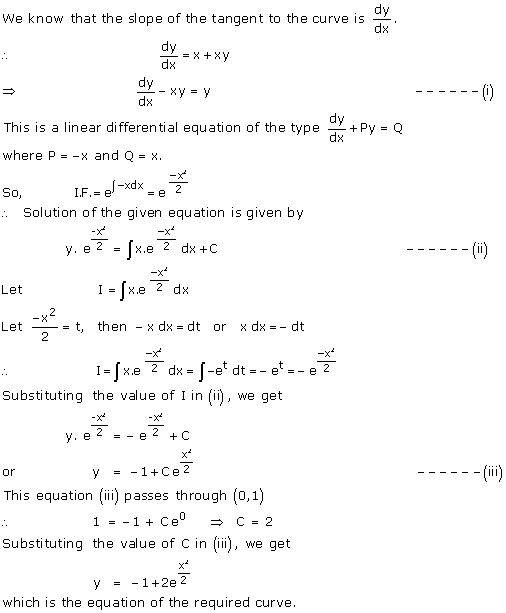
Solution 32

Solution 33

Solution 34

Differential Equations Exercise Ex. 22RE
Solution 1(i)
Solution 1(ii)
Solution 1(iii)
Solution 1(iv)
Solution 1(v)
Solution 1(vi)
Solution 1(vii)

Solution 2

Solution 3(i)

Solution 3(ii)

Solution 3(iii)

Solution 3(iv)

Solution 3(v)

Solution 3(vi)
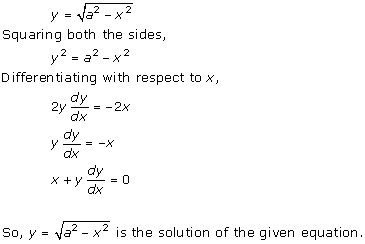
Solution 4
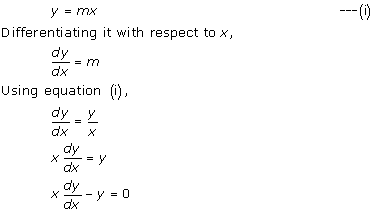
Solution 5
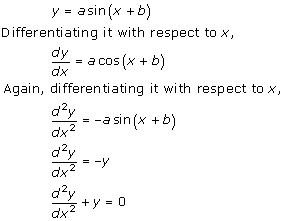
Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12
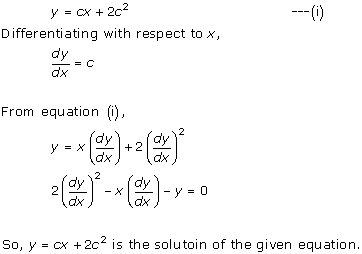
Solution 13
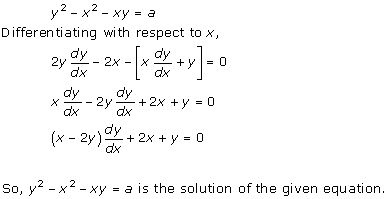
Solution 14
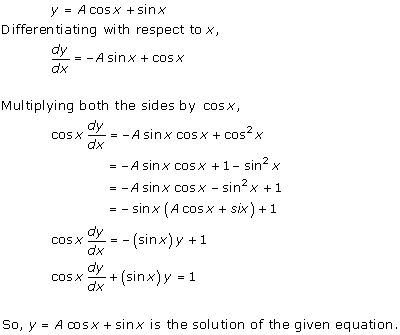
Solution 15

Solution 16

Solution 17
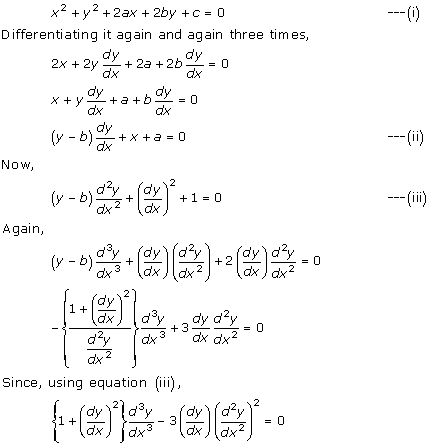
Solution 18

Solution 19
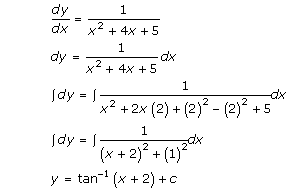
Solution 20

Solution 21

Solution 22

Solution 23
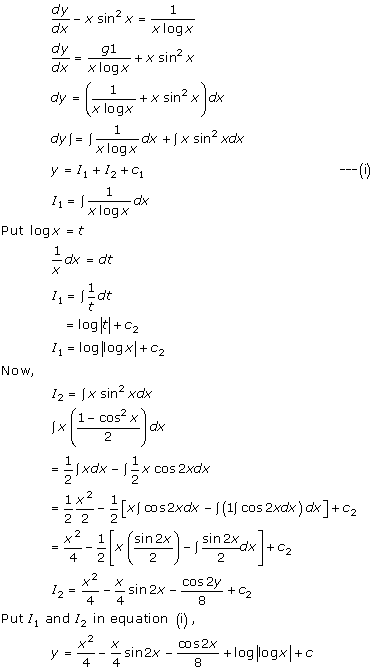
Solution 24

Solution 25

Solution 26
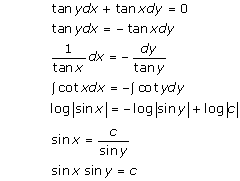
Solution 27

Solution 28

Solution 29

Solution 30

Solution 31

Solution 32
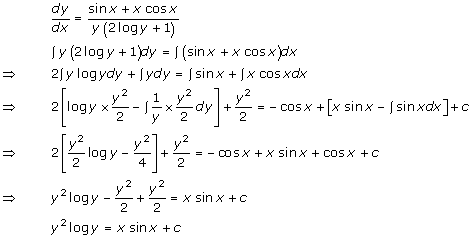
Solution 33

Solution 34
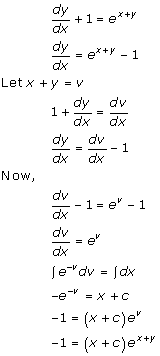
Solution 35
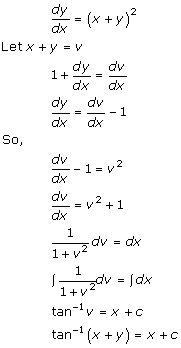
Solution 36
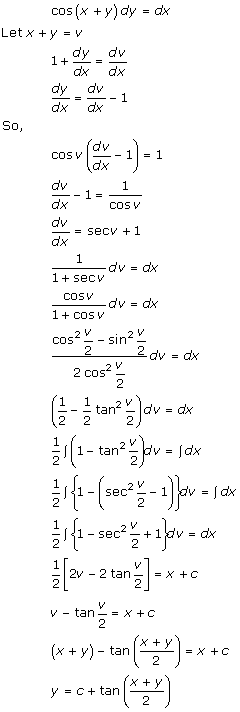
Solution 37
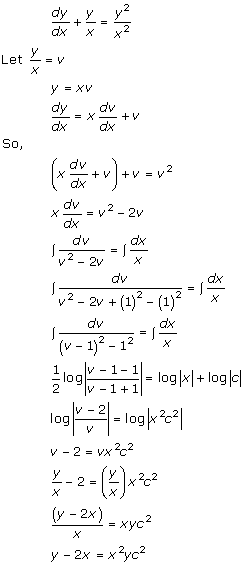
Solution 38
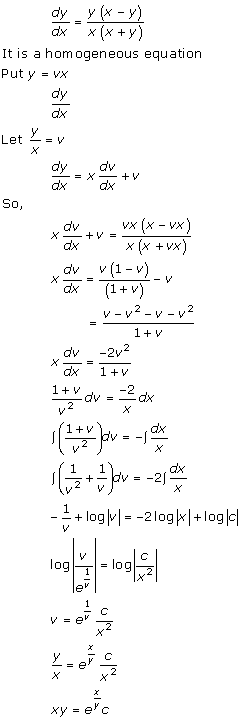
Solution 39
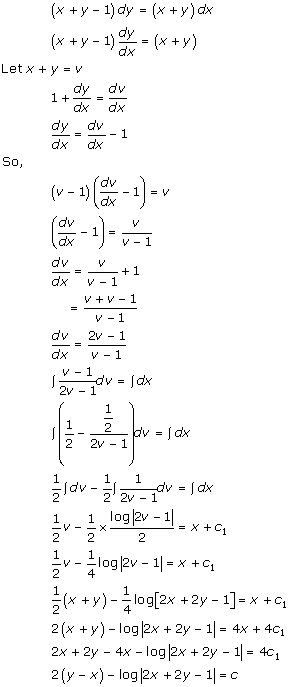
Solution 40

Solution 41
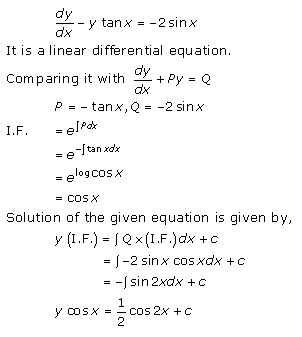
Solution 42
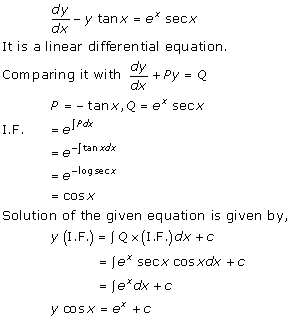
Solution 43

Solution 44
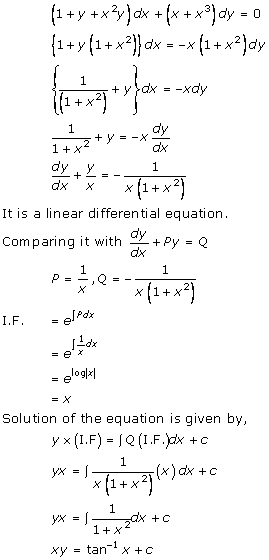
Solution 45

Solution 46
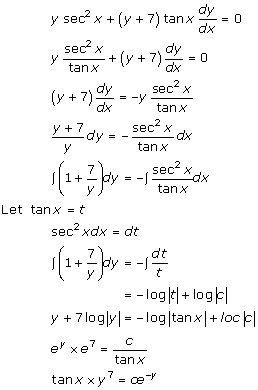
Solution 47

Solution 49

Solution 50

Solution 51

Solution 52
Solution 53
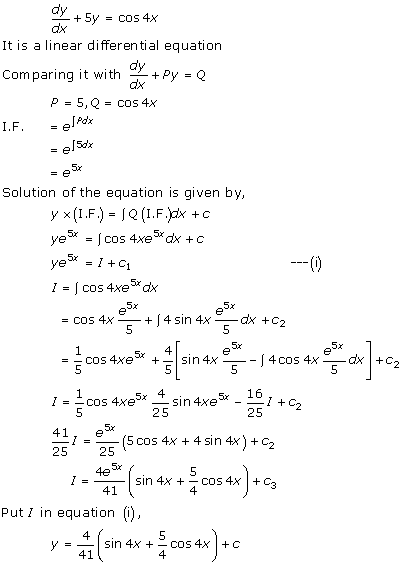
Solution 54

Solution 55

Solution 56
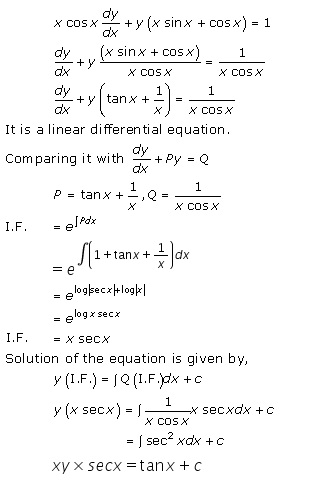
Solution 57

Solution 58
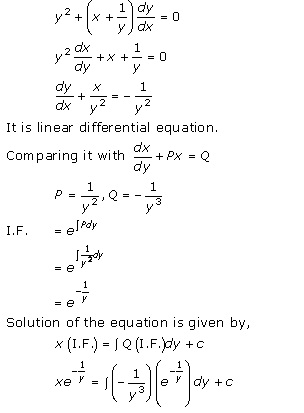
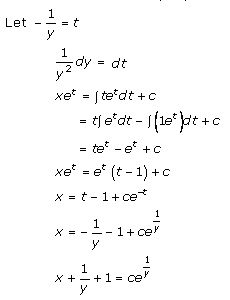
Solution 59

Solution 60

Solution 61
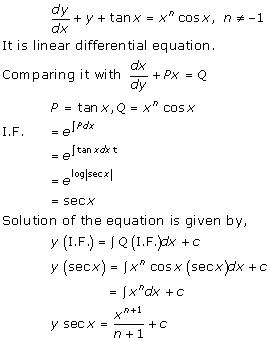
Solution 62

Solution 63
Solution 64(i)
Solution 64(ii)
Solution 64(iii)
Solution 64(iv)
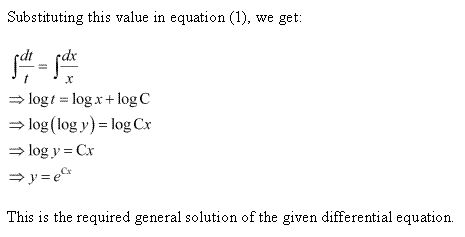
Solution 64(v)
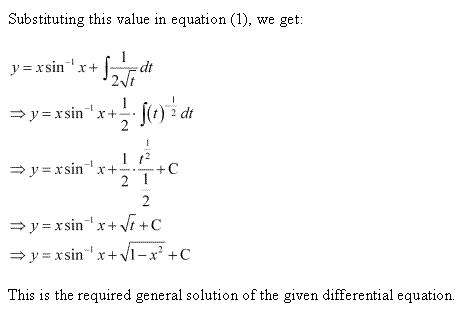
Solution 64(vi)
Solution 65(i)
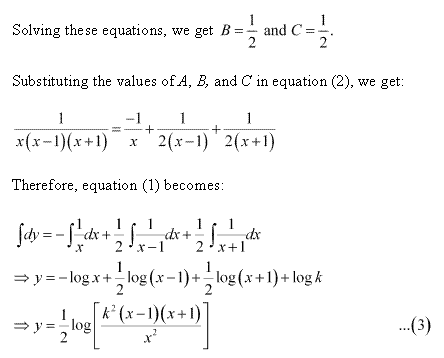
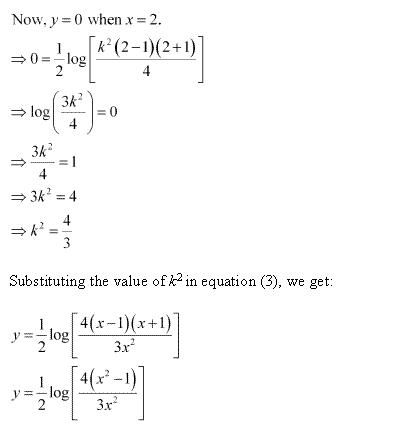
Solution 65(ii)
Solution 65(iii)
Solution 66(i)
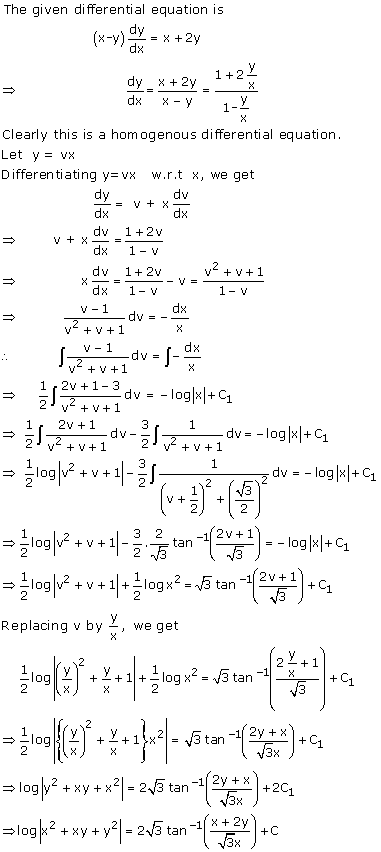
Solution 66(ii)
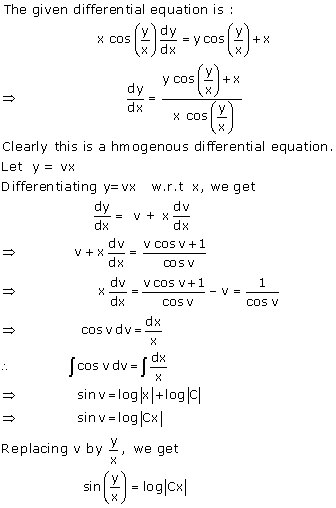
Solution 66(iii)
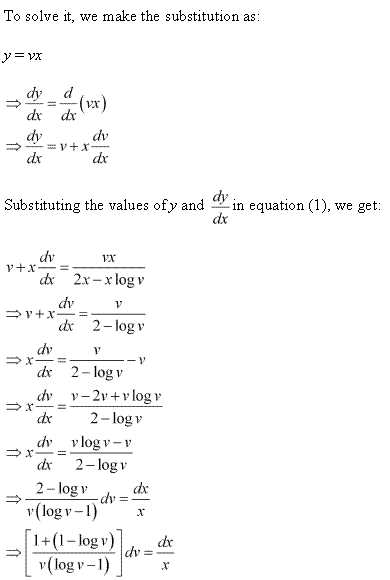
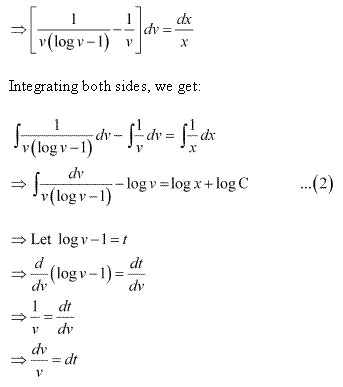
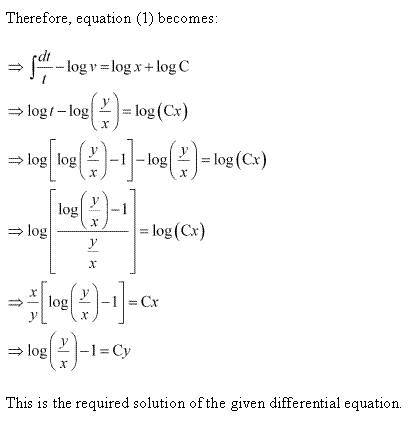
Solution 66(iv)
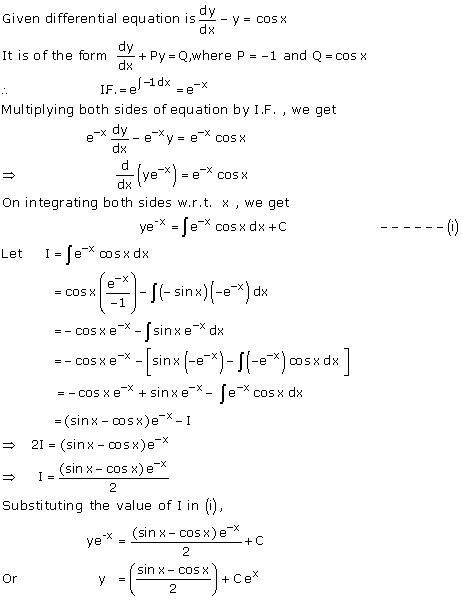
Solution 66(v)
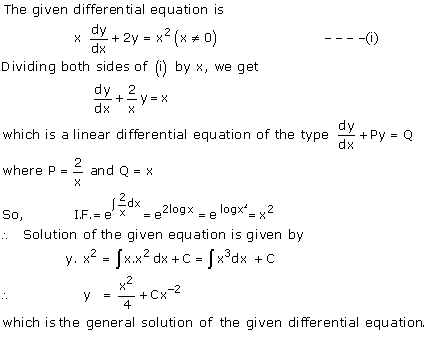
Solution 66(vi)

Solution 66(vii)
Solution 66(viii)
Solution 66(ix)
Solution 66(x)
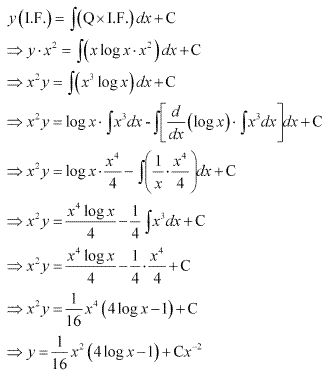
Solution 66(xi)
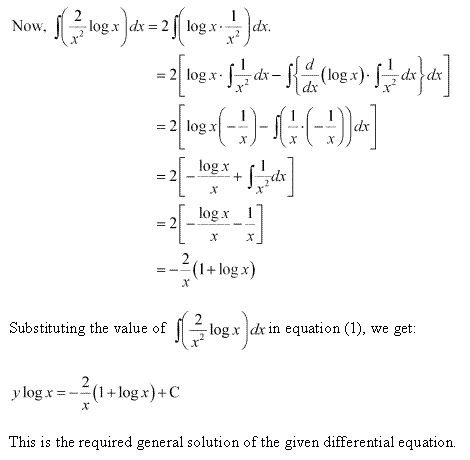
Solution 66(xii)
Solution 66(xiii)
Solution 66(xiv)
Solution 66(xv)
Solution 67(i)

Solution 67(ii)
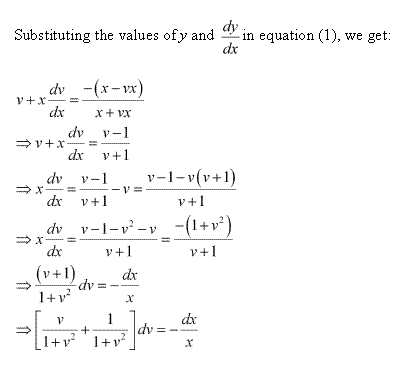

Solution 67(iii)

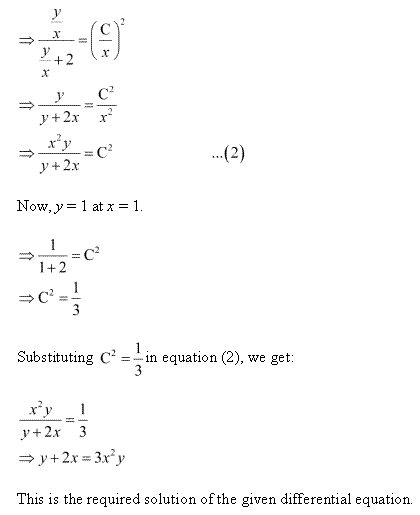
Solution 68
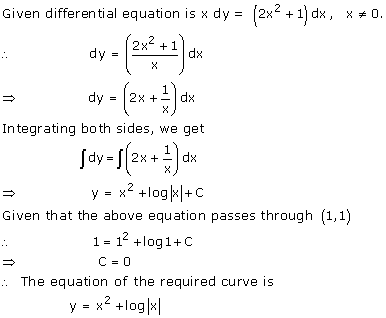
Solution 69

Solution 70

Solution 71

Solution 72

Solution 73
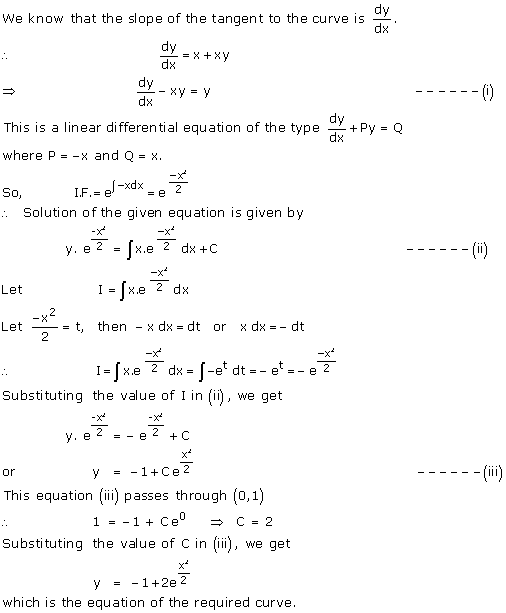
Solution 74

Solution 75
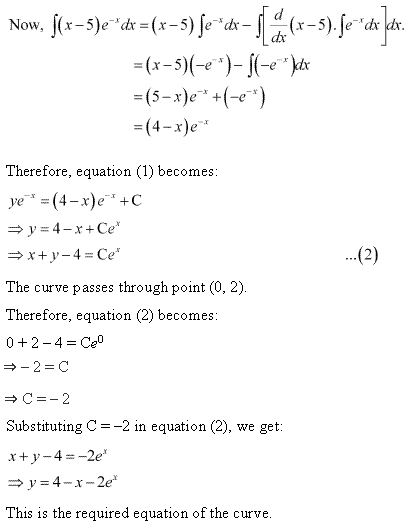
Solution 76
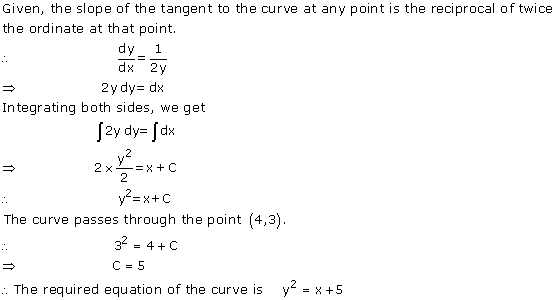
Solution 77

Solution 78
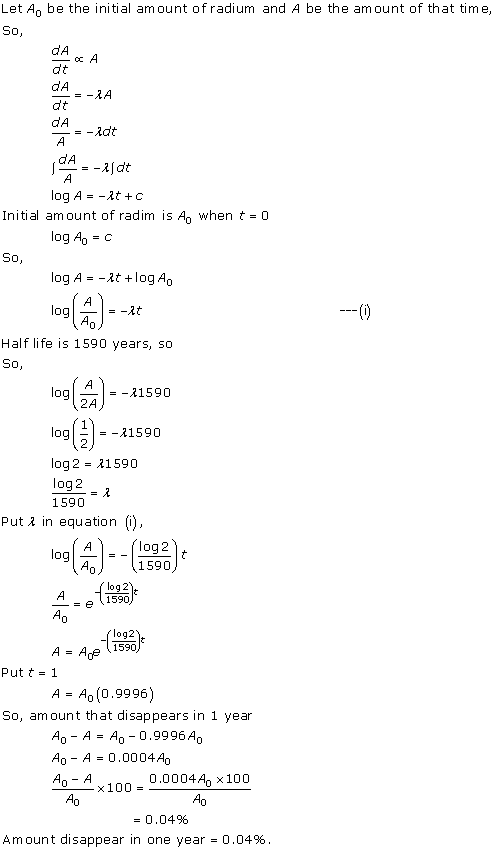
Solution 79

Differential Equations Exercise MCQ
Solution 1
Correct option: (c)

Solution 2
Correct option: (b)
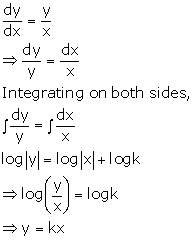
Solution 3
Correct option: (b)
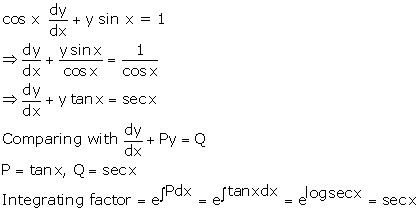
Solution 4
Correct option:(b)
Degree is the power of highest order derivative.
Highest order is 2 and its power is 2.
Hence, degree of differential equation is 2.
Solution 5

NOTE: Answer not matching with back answer.
Solution 6
Correct option:(d)

Solution 7
Correct option: (c)
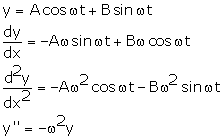
Solution 8
Correct option: (a)
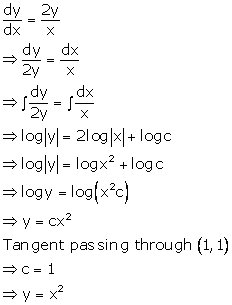
Solution 9
Correct option: (c)
Here, constants are c1, c2, c3, c4, c5, c6.
But c3+c4 is also constant. Hence, total 5 constants.
Solution 10
Correct option: (b)

Solution 11
Correct option: (a)

Solution 12
Correct option: (a)
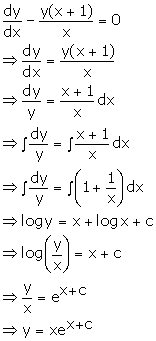
Solution 13
Correct option: (a)
Differential equation contains only one constant hence,
Order of differential equation is 1.
Solution 14
Correct option: (b)
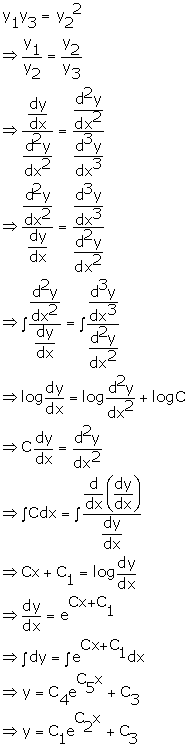
Solution 15
Correct option: (b)

Solution 16
Correct option: (d)

Solution 17
Correct option: (a)

Solution 18
Correct option: (a)

Solution 19
Correct option: (c)

Solution 20
Correct option: (d)

Solution 21
Correct option: (b)
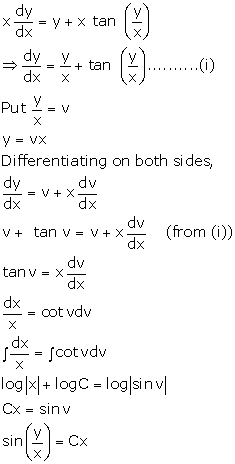
Solution 22
Correct option: (b)
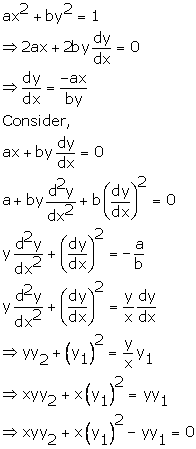
Solution 23
Correct option: (d)

Note: log is considered same as ln.
Solution 24
Correct option: (c)

Solution 25
Correct option:(a)

Solution 26
Correct option: (b)

Solution 27
Correct option: (d)

Solution 28
Correct option: (d)

Solution 29
Correct option: (a)
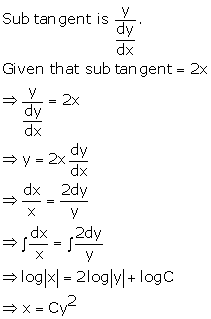
Solution 30
Correct option:(a)

Solution 31
Correct option:

Solution 32
Correct option: (b)
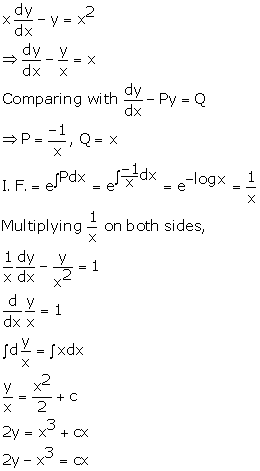
Solution 33
Correct option:(c)

Solution 34
Correct option: (d)

Solution 35
Correct option: (b)
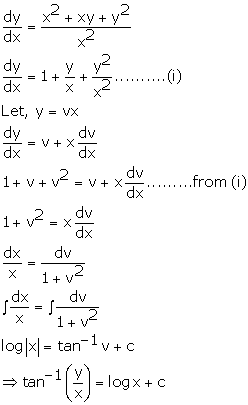
Solution 36
Correct option:(d)

Solution 37
Correct option: (c)
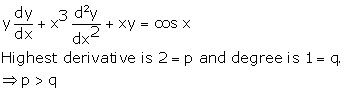
Note: Answer not matching with back answer.
Solution 38
Correct option: (c)

Solution 39
Correct option: (a)

Solution 40
Correct option: (c)

Solution 41
Correct option: (d)
Highest order derivative is 2 but equation cannot be expressed as a polynomial in differential equation.
Hence, it is not defined.
Solution 42
Correct option:(a)
Highest order of the derivative is 2.
Solution 43
Correct option: (d)
In the general solution of differential equation of order n has n number of arbitrary constants.
Solution 44
Correct option: (d)
The number of arbitrary constants in the particular solution of a differential equation of third order is always zer0.
Solution 45
Correct option: (b)
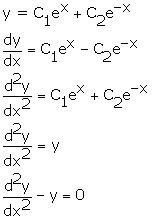
Solution 46
Correct option: (c)
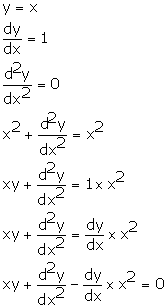
Solution 47
Correct option: (a)
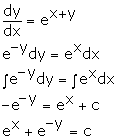
Solution 48
Correct option: (c)
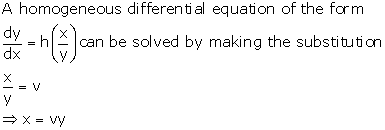
Solution 49
Correct option: (d)

Solution 50
Correct option: (c)
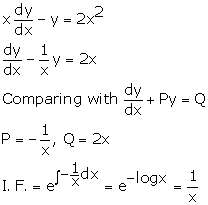
Solution 51
Correct option:(d)
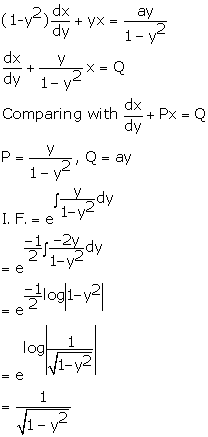
Solution 52
Correct option:(c)
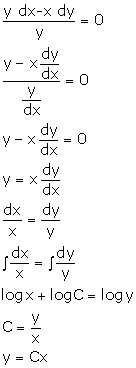
Solution 53
Correct option: (c)
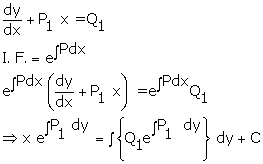
Solution 54
Correct option: (c)
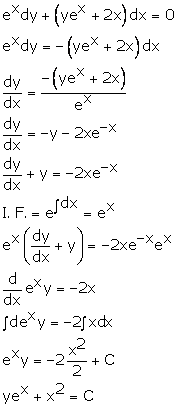
Differential Equations Exercise Ex. 22VSAQ
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5
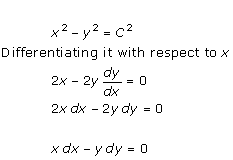
Solution 6
Solution 7
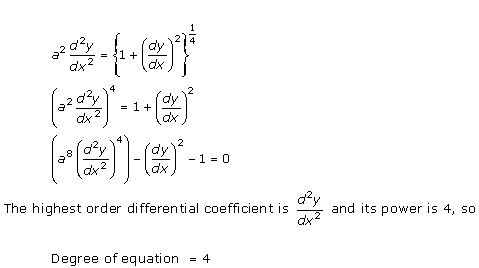
Solution 8
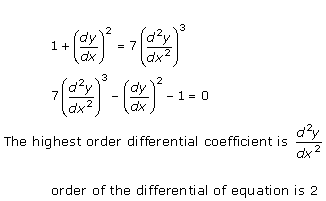
Solution 9

Solution 10
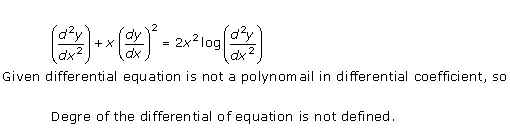
Solution 11

Solution 12

Solution 13

Solution 14

Solution 15
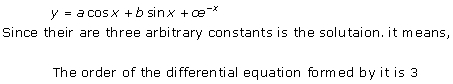
Solution 16

Solution 17

Solution 18
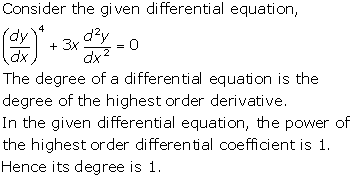
Solution 19
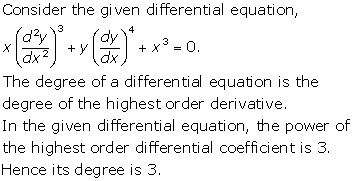
Solution 20

Solution 21