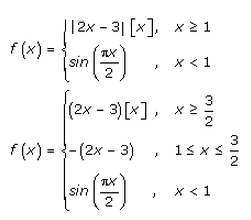Class 12-science RD SHARMA Solutions Maths Chapter 10 - Differentiability
Differentiability Exercise Ex. 10.1
Solution 1
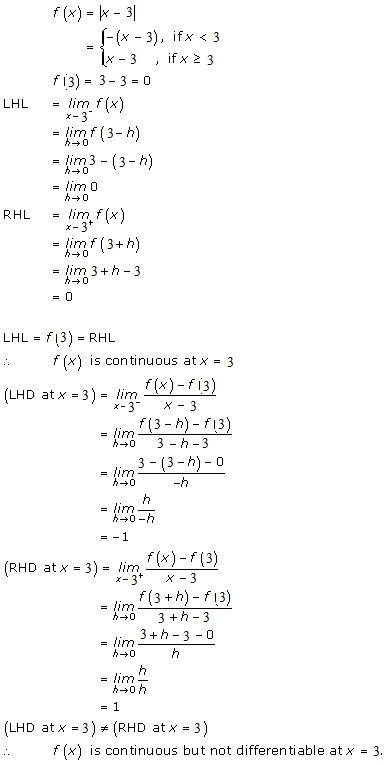
Solution 2
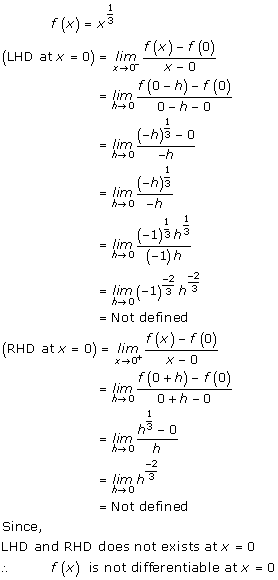
Solution 3

Solution 4
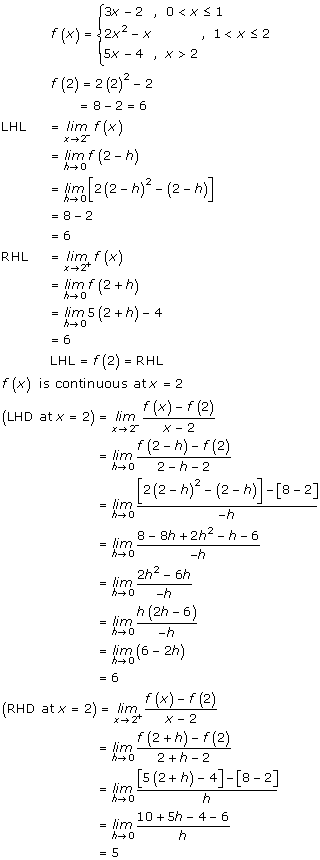
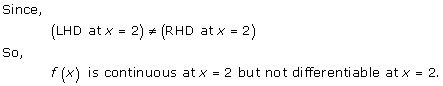
Solution 5

Solution 6

Solution 7(i)

Solution 7(ii)


Solution 7(iii)

Solution 8


Solution 9
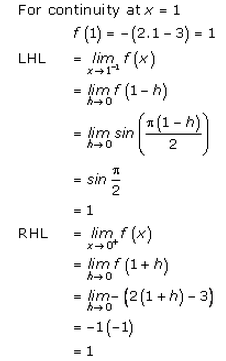
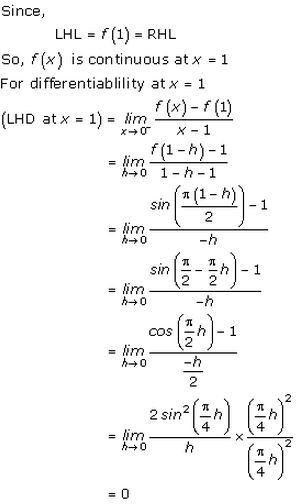
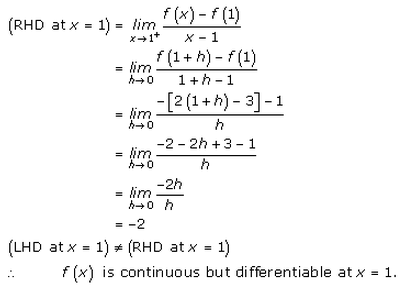
Solution 10
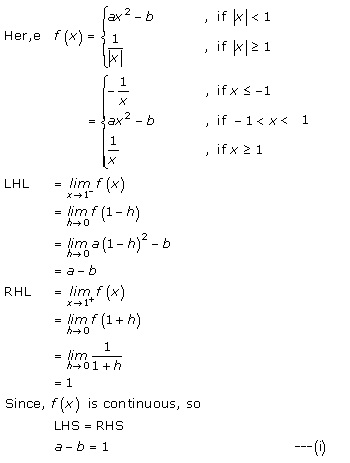
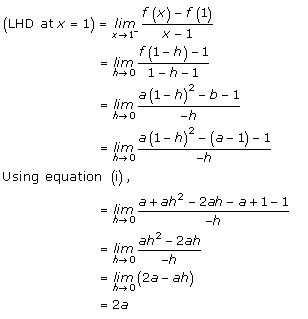
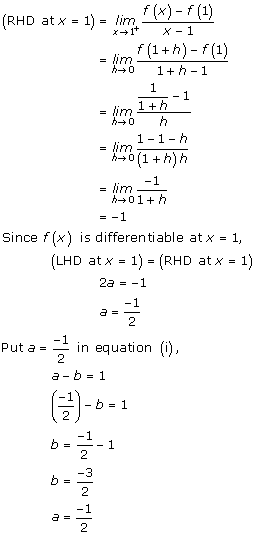
Solution 11
Given: ![]()
As f(x) is differentiable at x = 1, we have
![]() … (i)
… (i)
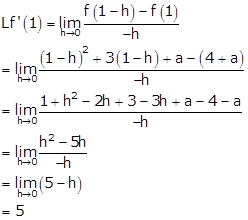

Now, Rf'(1) exist when (b - 2 - a) = 0 … (ii)
![]()
From (i), we get, b = 5
Putting this in (ii), we get, a = 3.
Differentiability Exercise Ex. 10.2
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

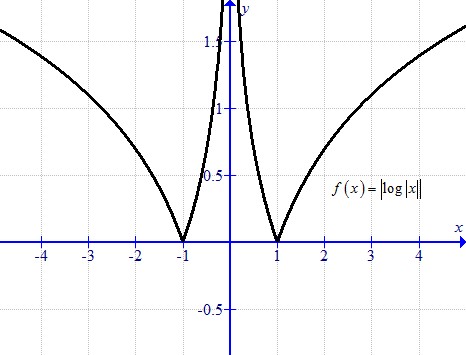
Solution 10

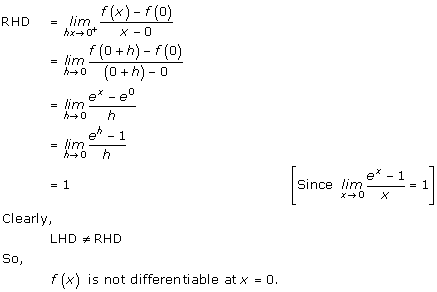
Solution 11

Solution 12

Differentiability Exercise MCQ
Solution 1
Correct option: (a)
Absolute value function is continuous on R.
Solution 2
Correct option: (b)

Solution 3
Correct option: (a)

Solution 4
Correct option: (b)

Solution 5
Correct option: (a), (c)
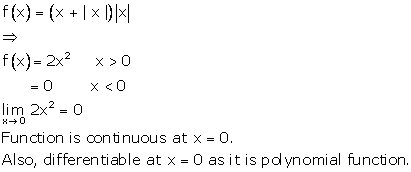
Solution 6
Correct option: (a)

Solution 7
![]()
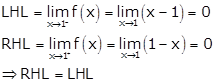
Therefore, f(x) is continuous at x = 1.
Now,
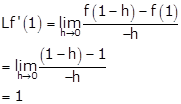
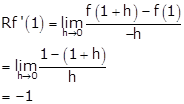
Therefore, Lf'(1) ≠ Rf'(1).
Hence, f(x) is not differentiable at x = 1.
Solution 8
Correct option: (b)

Solution 9
Correct option: (b)
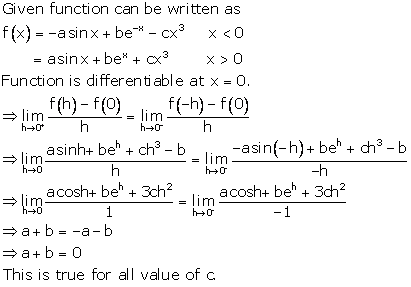
Solution 10
Correct option: (b)

Solution 11
Correct option: (a), (b)

Solution 12
Correct option: (b)
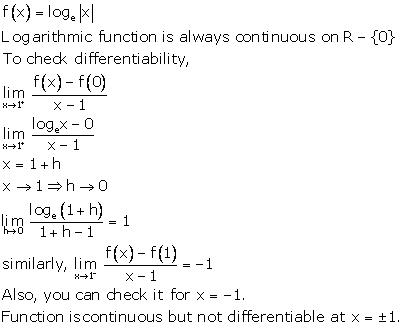
Solution 13
Correct option: (b)
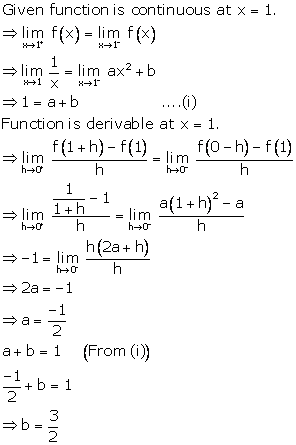
Solution 14
Correct option: (c)
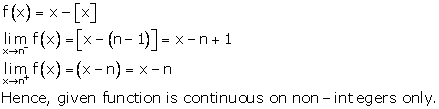
Solution 15
Correct option: (d)

Solution 16
Correct option: (b)
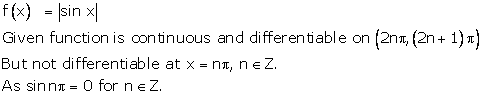
Solution 17
Correct option: (c)

Solution 18
Correct option: (b)

Solution 19
Correct option: (b)

Solution 20
Correct option: (a)
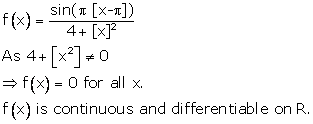
Solution 21
Correct option: (b)

Solution 22
Correct option: (d)

Solution 23
Correct option: (d)
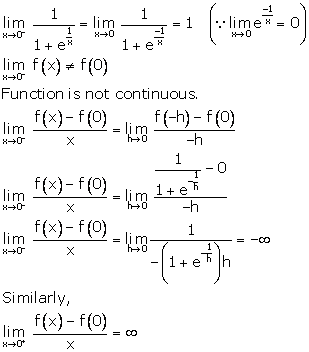
Solution 24
Correct option: (a)
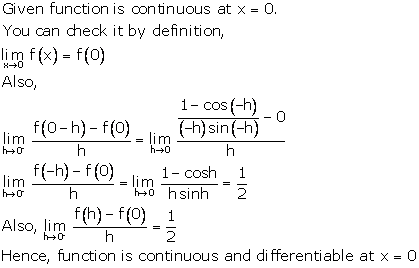
Solution 25
Correct option: (b)
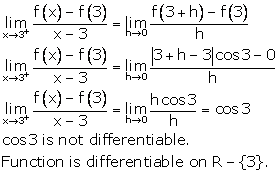
Solution 26
Correct option: (b)
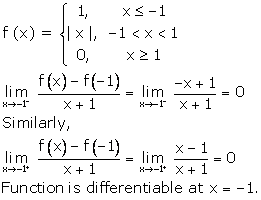
Solution 27
Given: 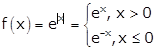
Now, f(x) is continuous everywhere except at x = 0.
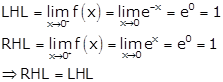
Therefore, f(x) is continuous everywhere.
Now,
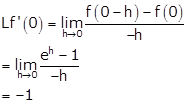
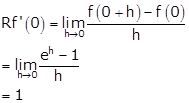
Therefore, Lf'(1) ≠ Rf'(1).
Thus, f(x) is not differentiable at x = 0.
Hence, f(x) is continuous everywhere but not differentiable at x = 0.
Solution 28
Given: 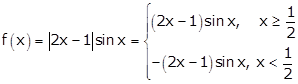
Now,

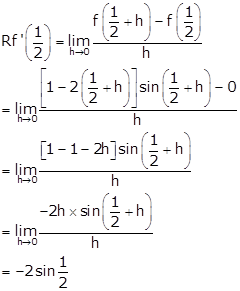
Therefore, Lf'(1) ≠ Rf'(1).
Thus, f(x) is not
differentiable at ![]()
Hence, the set of
points where f(x) is differentiable is ![]()
Differentiability Exercise Ex. 10VSAQ
Solution 1
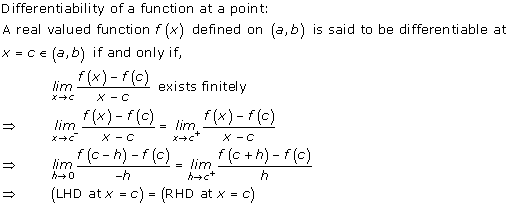
Solution 2
![]()
Solution 3
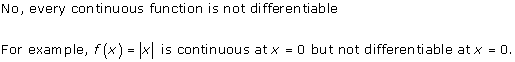
Solution 4

Solution 5
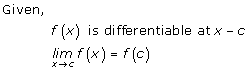
Solution 6

Solution 7
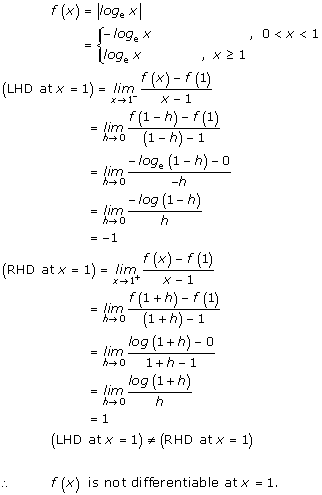
Solution 8
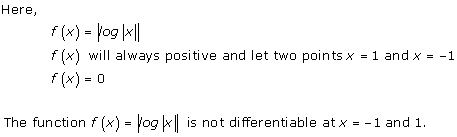
Solution 9

Solution 10
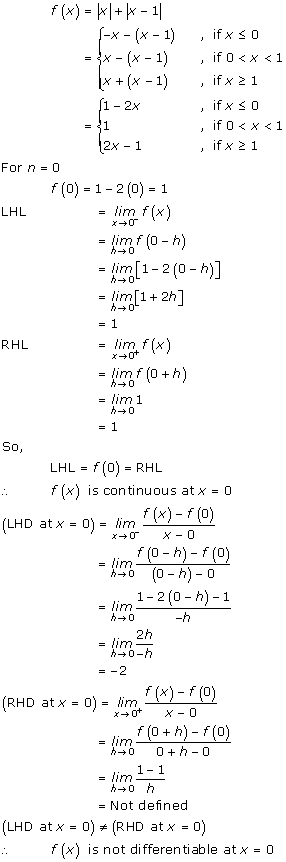
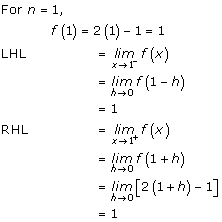
Solution 11
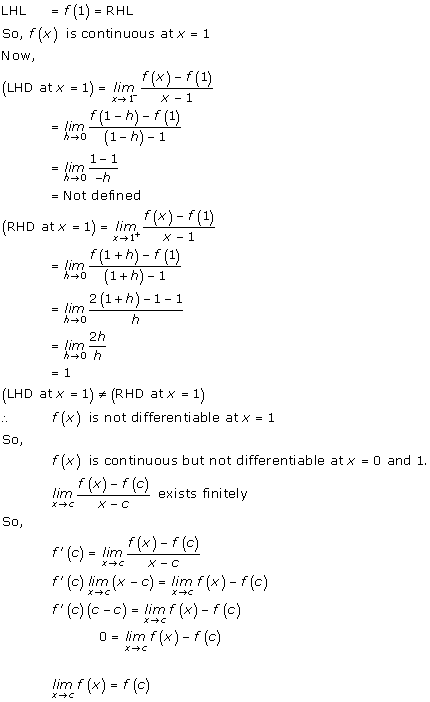
Solution 12
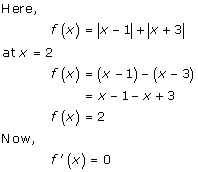
Solution 13