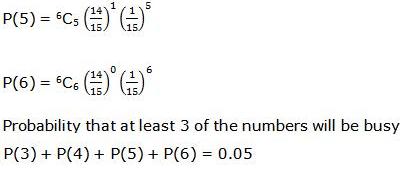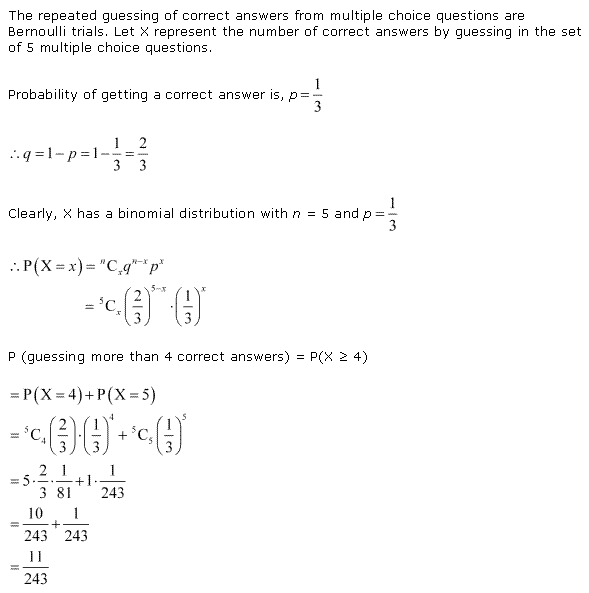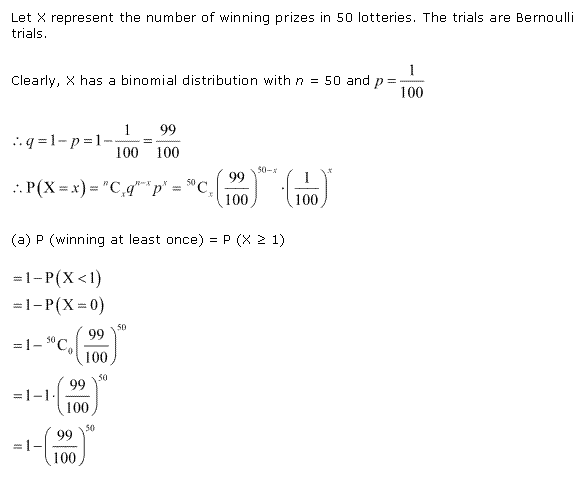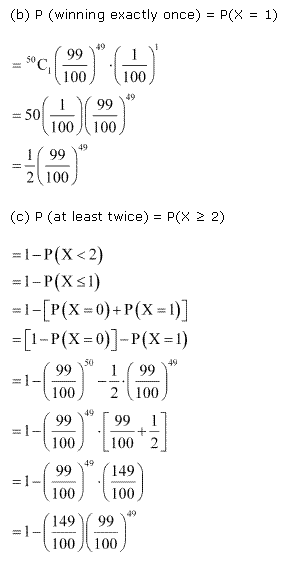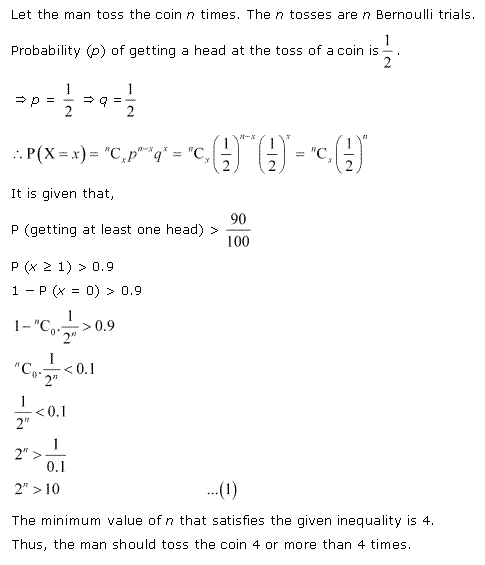Class 12-science RD SHARMA Solutions Maths Chapter 33 - Binomial Distribution
Binomial Distribution Exercise Ex. 33.1
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7
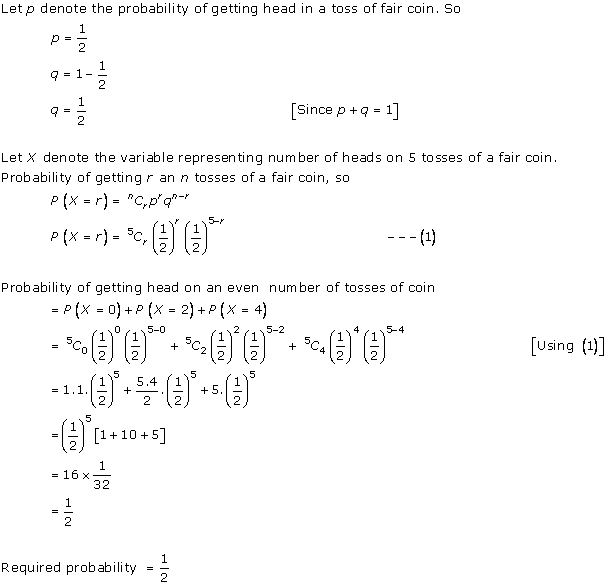
Solution 8

Required Probability =![]()
Solution 9
Solution 10

Solution 11

Solution 12


Solution 13


Solution 14

Solution 15

Solution 16

Solution 17


Solution 18
Solution 19

Solution 20



Solution 21



Solution 22



Solution 23



Solution 24
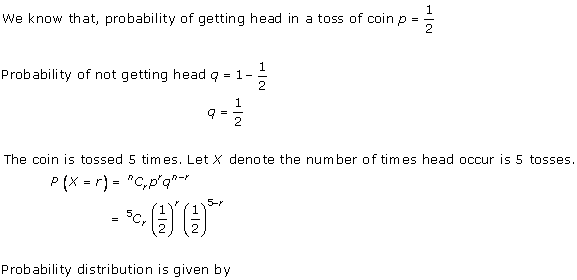


Solution 25



Solution 26

Solution 27
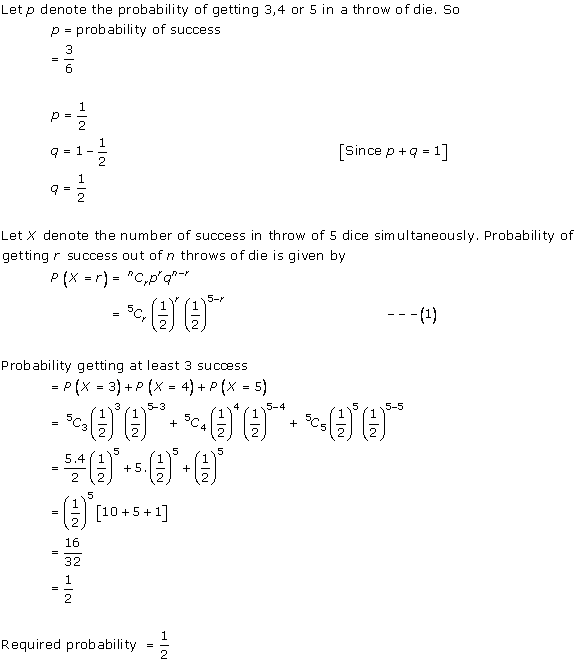
Solution 28

Solution 29

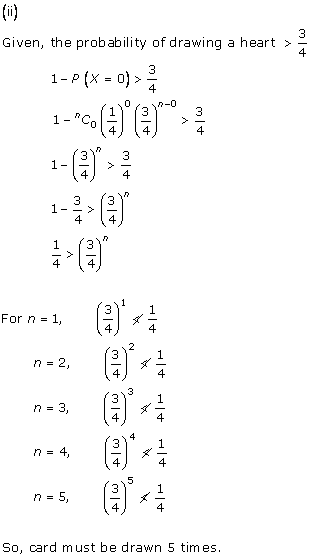
Solution 30
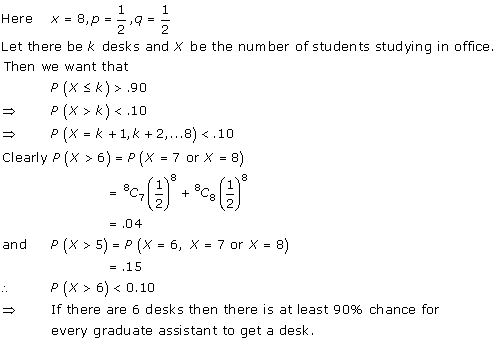
Solution 31
Solution 32



Solution 33

= 0.0256
Solution 34

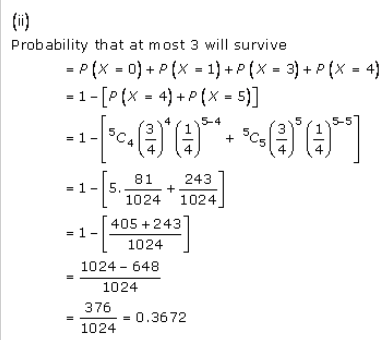
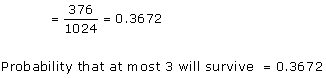
Solution 35
Solution 36

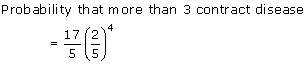
Solution 37

Solution 38
Solution 39

Solution 40

Solution 41

Solution 42
Solution 43
Solution 44
Solution 45
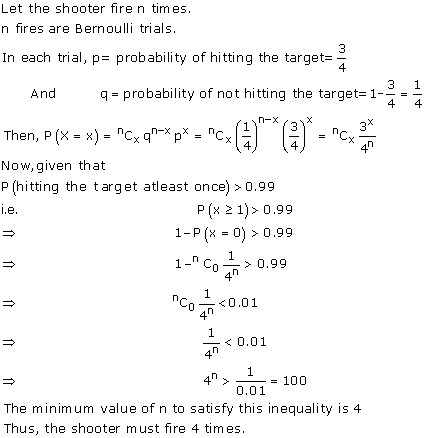
Solution 46
Solution 47
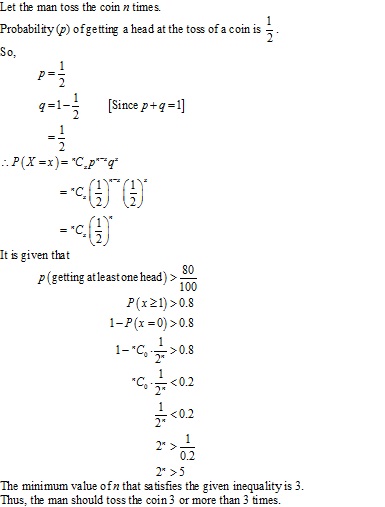
Solution 48

Solution 49

Solution 50

Solution 51

Solution 52

Solution 53

Note: Answer given in the book is incorrect.
Binomial Distribution Exercise Ex. 33.2
Solution 1

Solution 2
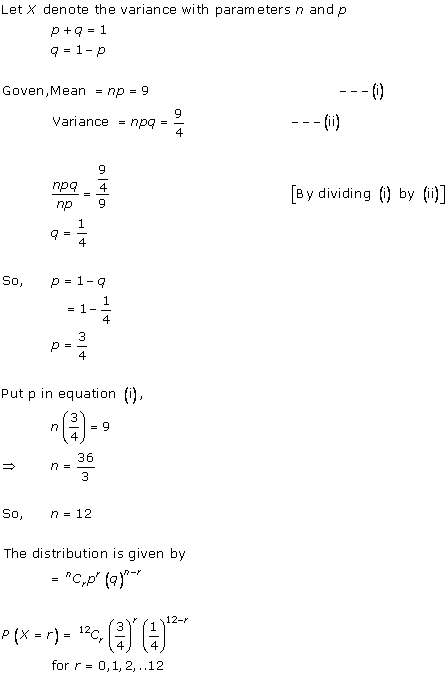
Solution 3

Solution 4

Solution 5

Solution 6


Solution 7

Solution 8
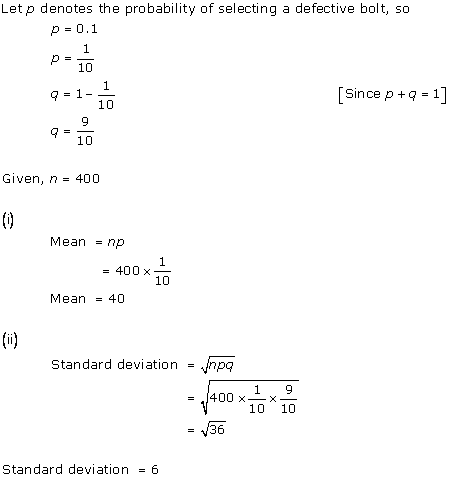
Solution 9
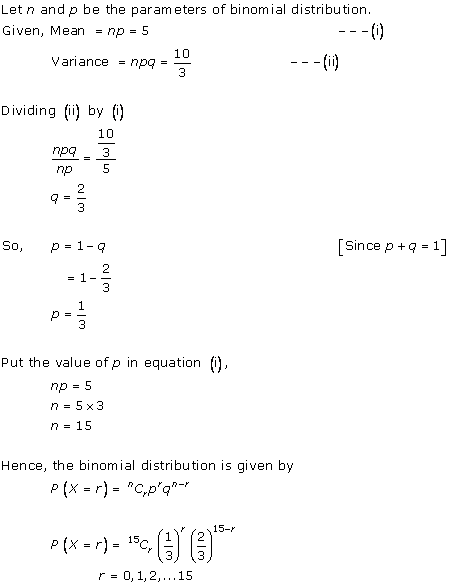
Solution 10

Solution 11


Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17
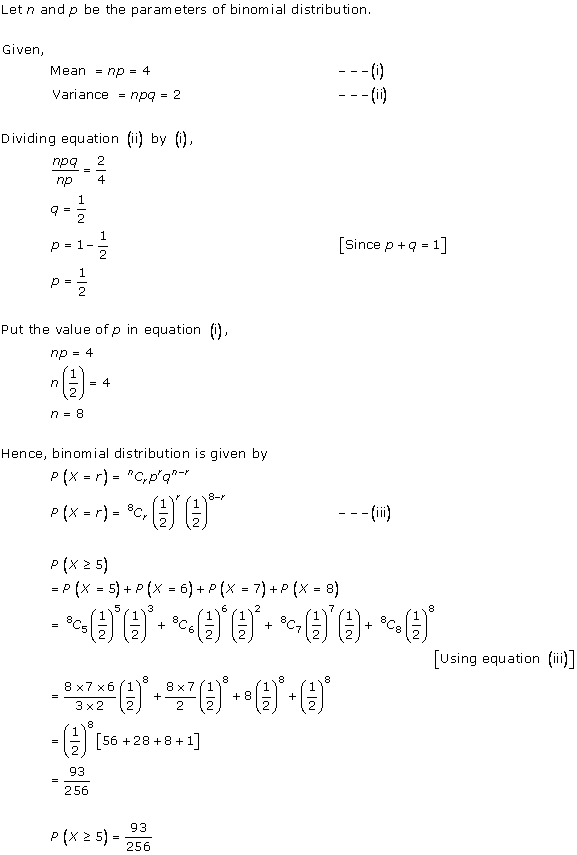
Solution 18


Solution 19

Solution 20

Solution 21

Solution 22
Out of 15 bulbs 5 are defective.

Solution 23

Solution 24
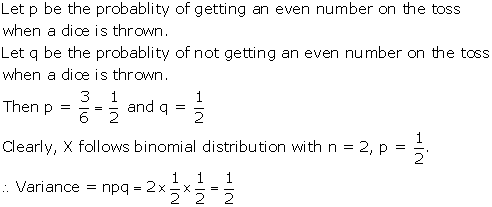
Solution 25

Binomial Distribution Exercise MCQ
Solution 1
Correct option: (a)

Solution 2
Correct option: (b)

Solution 3
Correct option: (c)

Solution 4
Correct option: (c)

Solution 5
Correct option: (a)

Solution 6
Correct option: (c)

Solution 7
Correct option: (a)

Solution 8
Correct option: (a)

Solution 9
Correct option: (b)

Solution 10
Correct option: (a)

Solution 11
Correct option: (d)

Solution 12
Correct option: (d)

Solution 13
Correct option: (a)

Solution 14
Correct option: (b)

Solution 15
Correct option: (c)
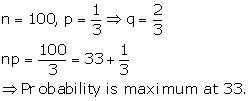
Solution 16
Correct option: (b)
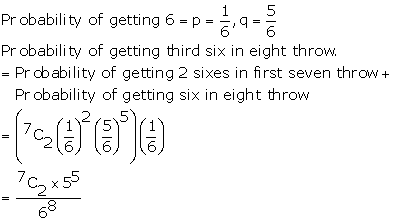
Solution 17
Correct option: (d)

Solution 18
Correct option: (d)

NOTE: Answer not matching with back answer.
Solution 19
Correct option: (b)
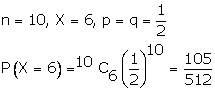
Solution 20
Correct option: (b)
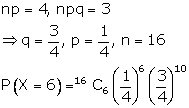
Solution 21
Correct option: (c)
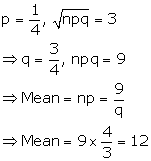
Solution 22
Correct option: (d)

Solution 23

NOTE: Answer not matching with back answer.
Solution 24
Correct option: (b)

Solution 25
Correct option: (d)

Solution 26
Correct option: (d)

Solution 27
Correct option: (a)

Solution 28
Correct option: (a)
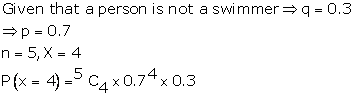
Solution 29
Correct option: (c)
In Binomial distribution trails are independent.
Solution 30
Correct option: (b)

Binomial Distribution Exercise Ex. 33VSAQ
Solution 1
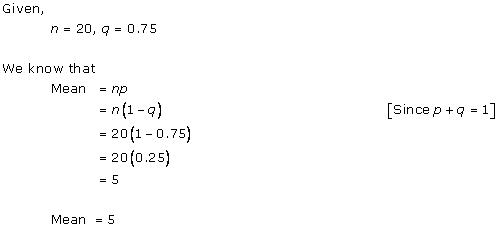
Solution 2

Solution 3

Solution 4

Solution 5

![]()
Solution 6

Solution 7
Solution 8

Solution 9