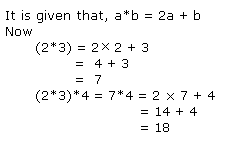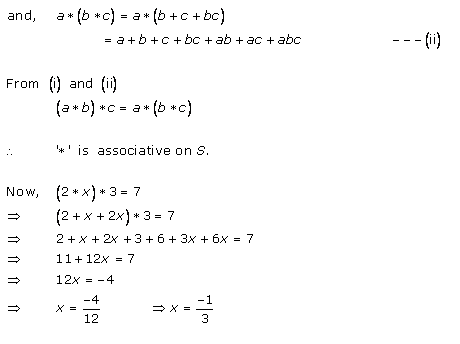Class 12-science RD SHARMA Solutions Maths Chapter 3 - Binary Operations
Binary Operations Exercise Ex. 3.1
Solution 1(i)

Solution 1(ii)
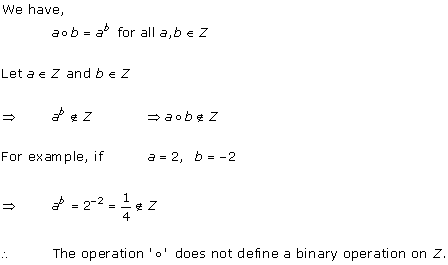
Solution 1(iii)

Solution 1(iv)

Solution 1(v)

Solution 1(vi)
We have,
A ⊙ b = ab + ba for all a, b, ϵ N
Let a ϵ N and b ϵ N
⇒ ab ϵ N and ba ϵ N
⇒ ab + ba ϵ N
⇒ a ⊙ b ϵ N
Thus, the operation ‘⊙’ defines a binary relation on N
Solution 1(vii)

Solution 2
Solution 3
It is given that, a*b = 2a + b - 3
now,
3*4 = 2 × 3 + 4 - 3
= 10 - 3
= 7
Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9
Solution 10
Binary Operations Exercise Ex. 3.2
Solution 1

Solution 2

Solution 3

Solution 4(i)

Solution 4(ii)

Solution 4(iii)

Solution 4(iv)
'⊙' on Q defined by a⊙b = a2 + b2 for all a, b ϵ Q
Commutativity:
For a, b ϵ Q
a⊙b = a2 + b2 = b2 + a2 = b⊙a
So, '⊙' is commutative on Q.
Associativity:
For a, b, c ϵ Q
(a⊙b) ⊙c = (a2 + b2) ⊙c = (a2 + b2)2 + c2
a⊙(b ⊙c) =a ⊙( b2 +c2)= a2 +(b2 + c2 )2
(a⊙b) ⊙c ≠ a⊙(b ⊙c)
So, '⊙' is not associative on Q.
Solution 4(v)

Solution 4(vi)

Solution 4(vii)

Solution 4(viii)

Solution 4(ix)
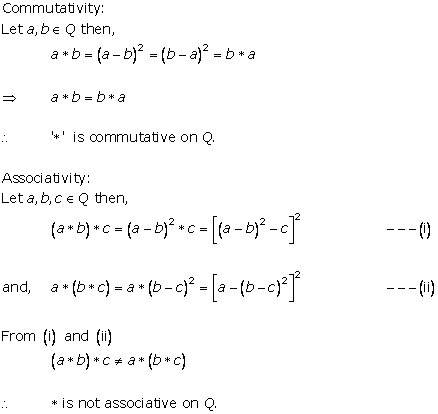
Solution 4(x)

Solution 4(xi)
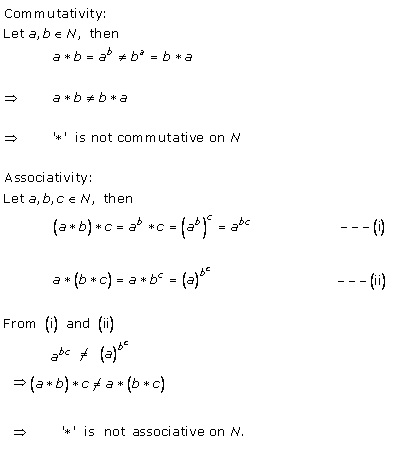
Solution 4(xii)

Solution 4(xiii)

Solution 4(xiv)
'*' on Q defined by a*b = a + b - ab for all a, b ϵ Z
Commutativity:
For a, b ϵ Z
a*b = a + b - ab = b + a - ba = b*a
So, '*' is commutative on Z.
Associativity:
For a, b, c ϵ Z
(a*b) *c = (a + b - ab) *c
= a + b - ab + c + ac + bc - abc
a*(b*c )= a*( b + c - bc)
= a + b +c - bc + ab + ac + - abc
(a*b) *c ≠ a*(b*c )
So, '*' is not associative on Z.
Solution 4(xv)
'*' on Q defined by a*b = gcd (a, b) for all a, b ϵ N
Commutativity:
For a, b ϵ Q
a*b = gcd (a, b) = gcd (b, a) = b*a
So, '*' is commutative on N.
Associativity:
For a, b, c ϵ N
(a*b) *c = (gcd (a, b)) *c
= gcd (a, b, c)
=a*( gcd (b, c))
=a*(b*c)
(a*b) *c = a*(b*c )
So, '*' is associative on N.
Solution 5

Solution 6

Solution 7

Solution 8
Now consider (a * b) * c.
Thus, we have, (a * b) * c = (a + b + ab) * c
= a + b + ab + c +(a + b + ab)c
= a + b + ab + c + ac + bc + abc
= a + b + c + ab + ac + bc + abc ---(i)
Solution 9

Solution 9
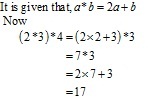
Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Binary Operations Exercise Ex. 3.3
Solution 1
Solution 2

Solution 3

Solution 4

Binary Operations Exercise Ex. 3.4
Solution 1

Solution 2

Solution 3

Solution 4
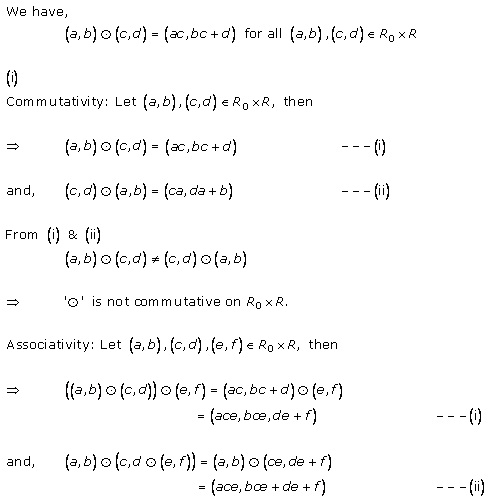

Solution 5

Solution 6

Solution 7
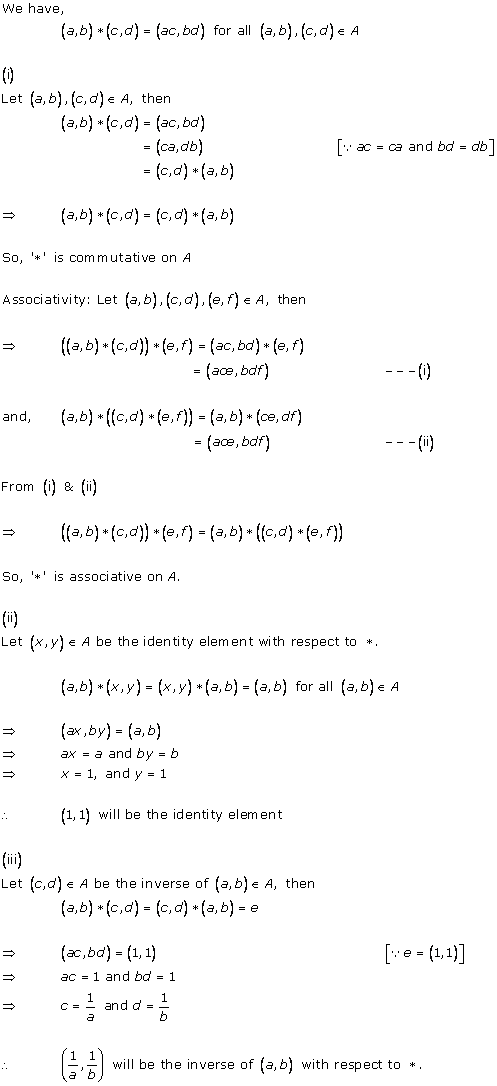
Solution 8

Binary Operations Exercise Ex. 3.5
Solution 1

Solution 2

Solution 3

Solution 4
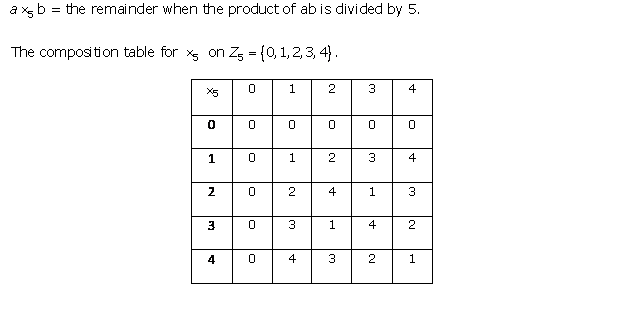
Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

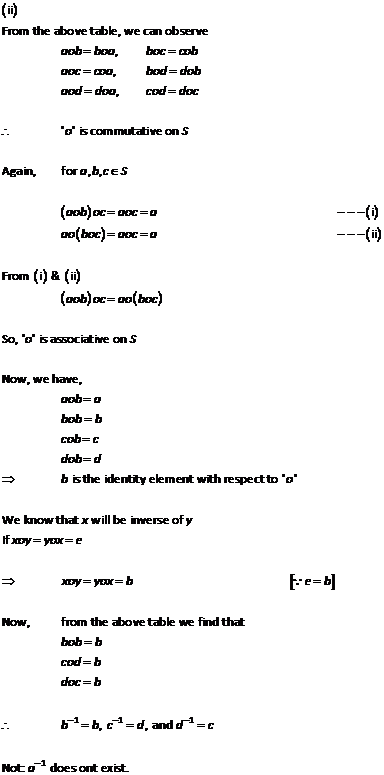
Solution 10

Binary Operations Exercise MCQ
Solution 1

Solution 2
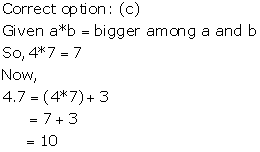
Solution 3

Solution 4
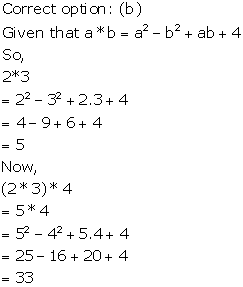
Solution 5

Solution 6
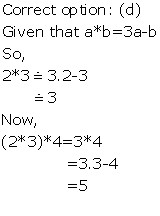
Solution 7

Solution 8
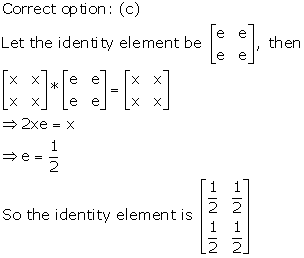
Solution 9

Solution 10
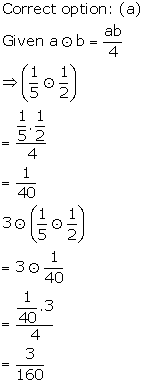
Solution 11

Solution 12

Solution 13
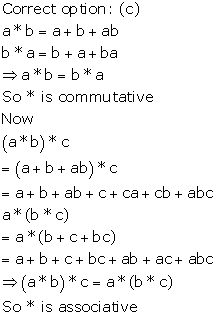
Solution 14

Solution 15
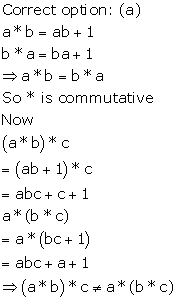
Solution 16

Solution 17
![]()
Solution 18

Solution 19
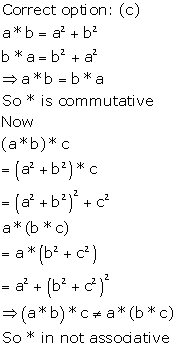
Solution 20
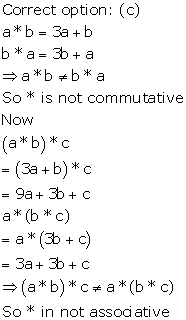
Solution 21

Solution 22

Solution 23

Solution 24

Solution 25
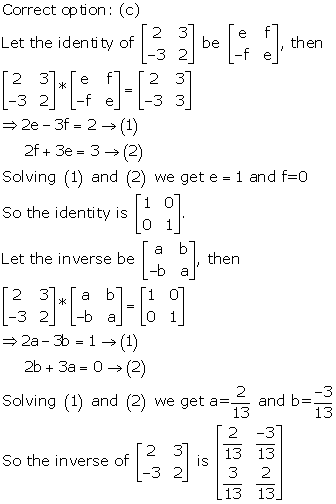
Solution 26

Solution 27

Solution 28
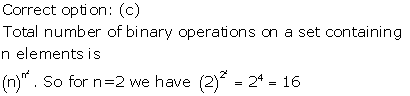
Solution 29
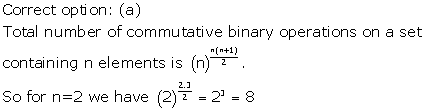
Binary Operations Exercise Ex.3VSAQ
Solution 1
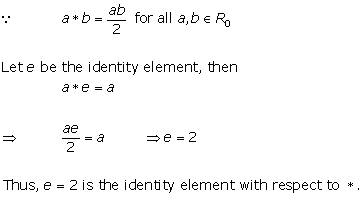
Solution 2

Solution 3
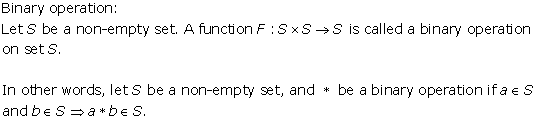
Solution 4

Solution 5

Solution 6

Solution 7
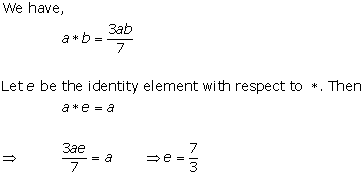
Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17
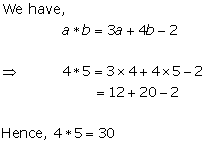
Solution 18
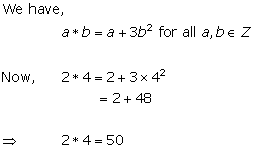
Solution 19

Solution 20
![]()