Class 12-science RD SHARMA Solutions Maths Chapter 5 - Algebra of Matrices
Algebra of Matrices Exercise MCQ
Solution 46
As A and B are symmetric matrices, we have
AT = A and BT = B … (i)
Consider,
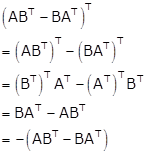
Hence, ABT - BAT is a skew-symmetric matrix.
Solution 1
Solution 2
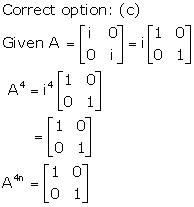
Solution 3
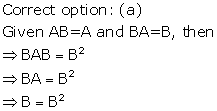
Solution 4

Solution 5

Solution 6
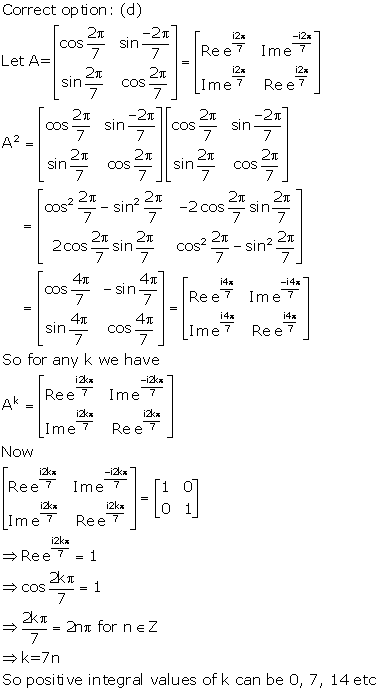
Solution 7

Solution 8
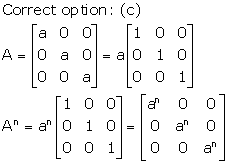
Solution 9

Solution 10
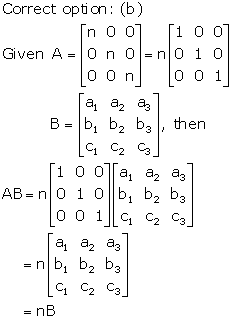
Solution 11

Solution 12

Solution 13
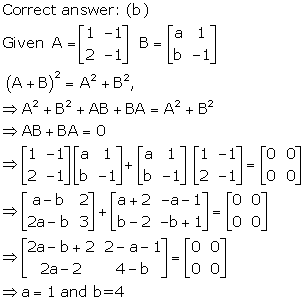
Solution 14

Solution 15
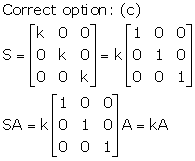
Solution 16

Solution 17

Solution 18
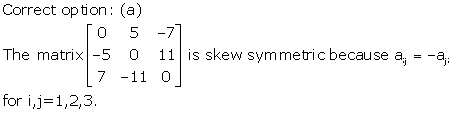
Solution 19
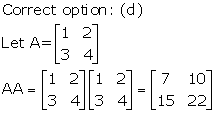
Solution 20

Solution 21
![]()
Solution 22
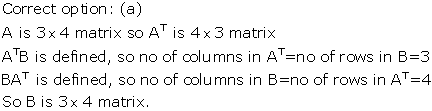
Solution 23
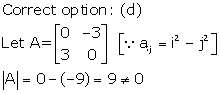
Solution 24
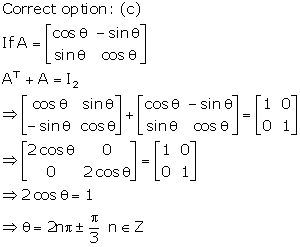
Solution 25
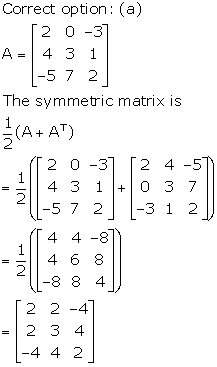
Solution 26
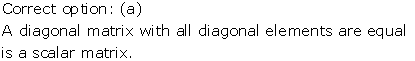
Solution 27

Solution 28

Solution 29
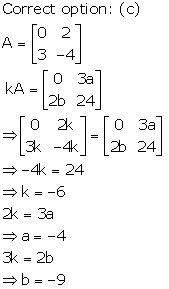
Solution 30
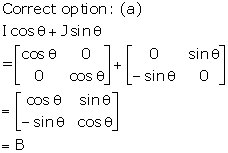
Solution 31
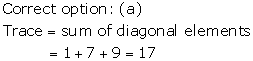
Solution 32
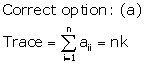
Solution 33
![]()
Solution 34

Solution 35
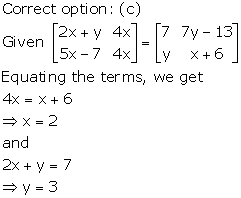
Solution 36
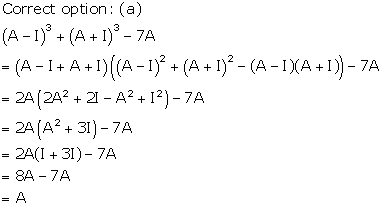
Solution 37

Solution 38

Solution 39

![]()
Solution 40
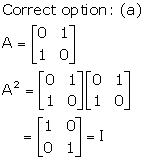
Solution 41
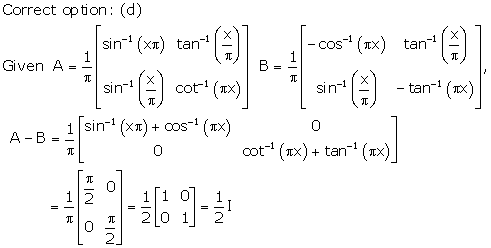
Solution 42
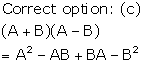
Solution 43

Solution 44
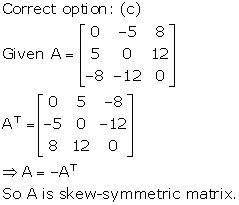
Solution 45
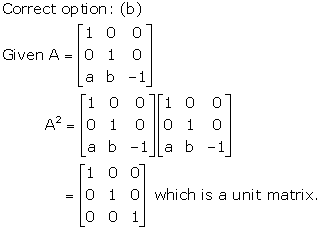
Correct option: (d)
A matrix is called Diagonal matrix if all the elements, except those in the leading diagonal, are zero.
Algebra of Matrices Exercise Ex. 5.1
Solution 1
We know that if a matrix is of the order ![]() , it has mn elements. Thus, to find all the possible orders of a matrix having 8 elements, we have to find all the ordered pairs of natural numbers whose products is 8.
, it has mn elements. Thus, to find all the possible orders of a matrix having 8 elements, we have to find all the ordered pairs of natural numbers whose products is 8.
The ordered pairs are: ![]()
![]() are the ordered pairs of natural numbers whose product is 5.
are the ordered pairs of natural numbers whose product is 5.
Hence, the possible orders of a matrix having 5 elements are ![]()
Solution 2
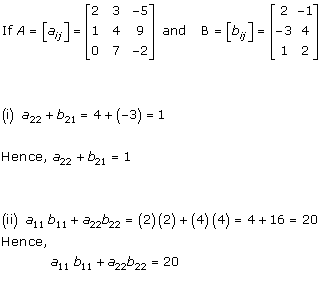
Solution 3

Solution 4
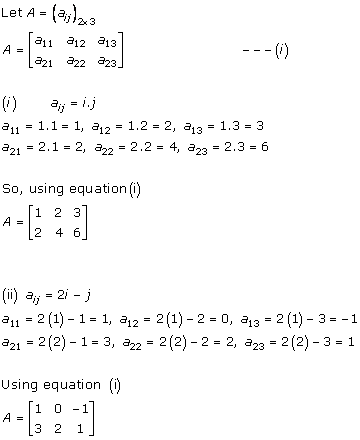
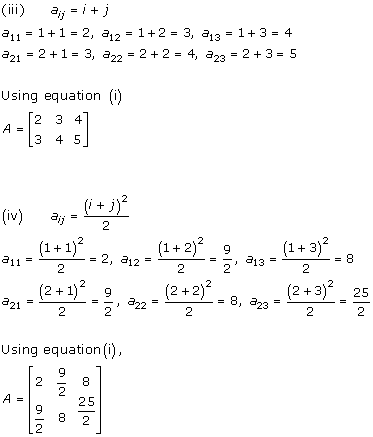
Solution 5
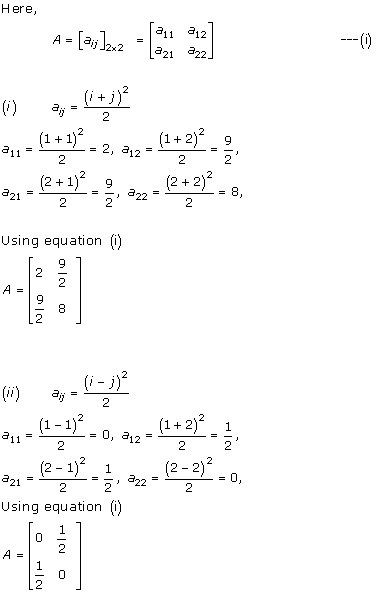



Solution 5(vii)
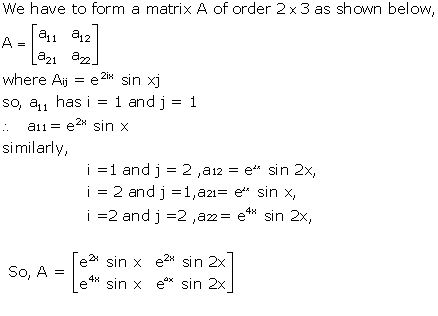
Solution 6

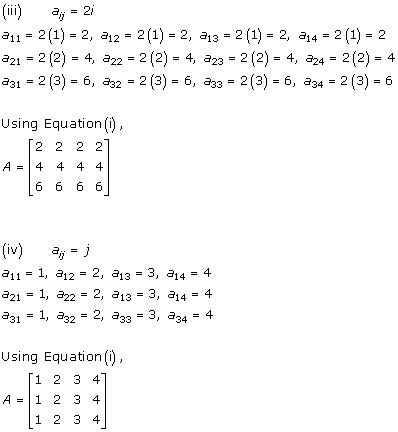

Solution 7

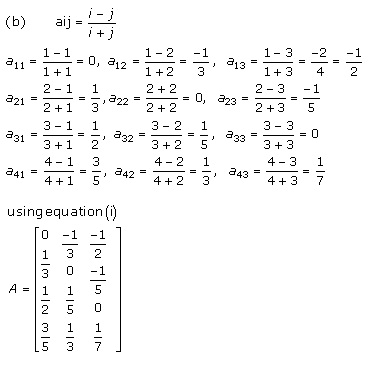
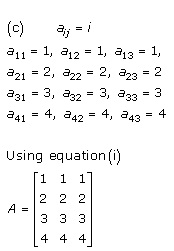
Solution 8
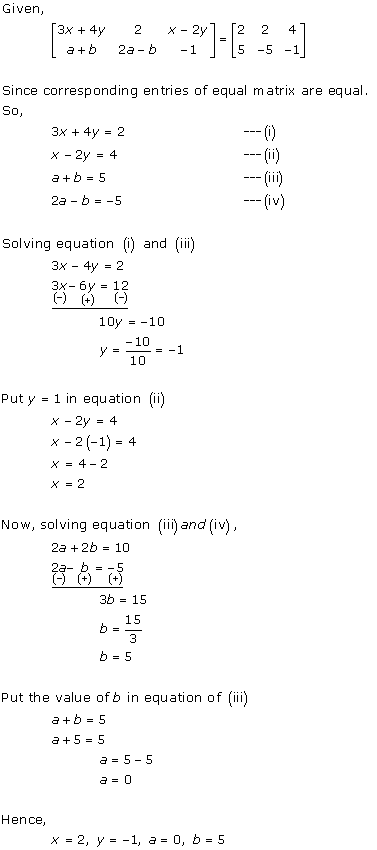
Solution 9
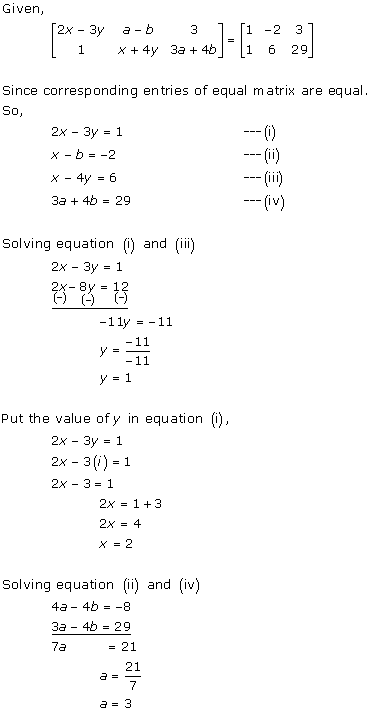
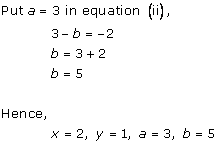
Solution 10

Solution 11
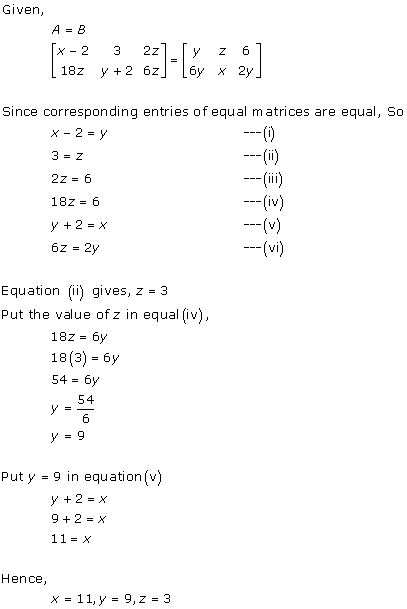
Solution 12
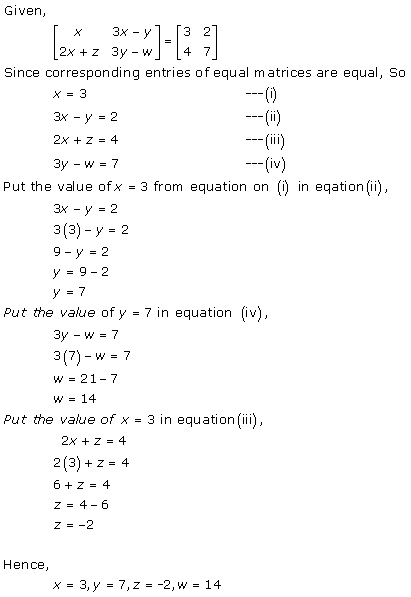
Solution 13

Solution 14
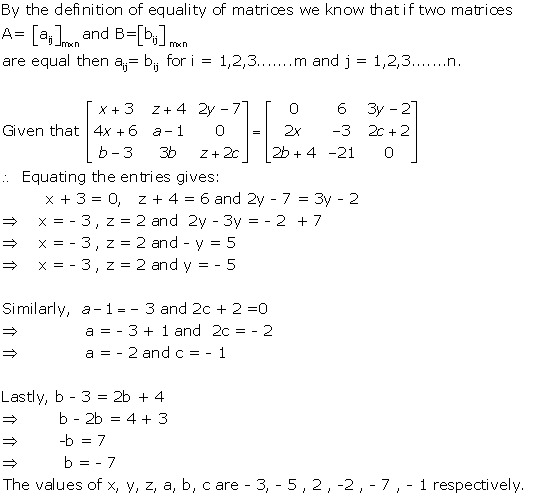
Solution 15
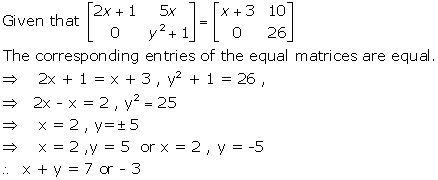
Solution 16
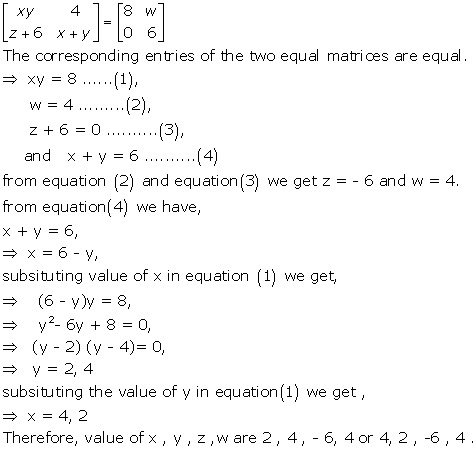
Solution 17

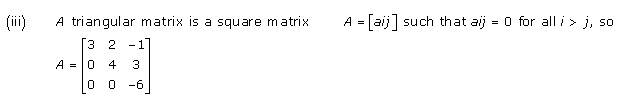
Solution 18
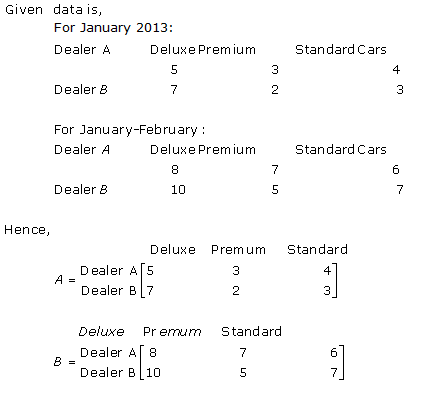
Solution 19

Solution 20
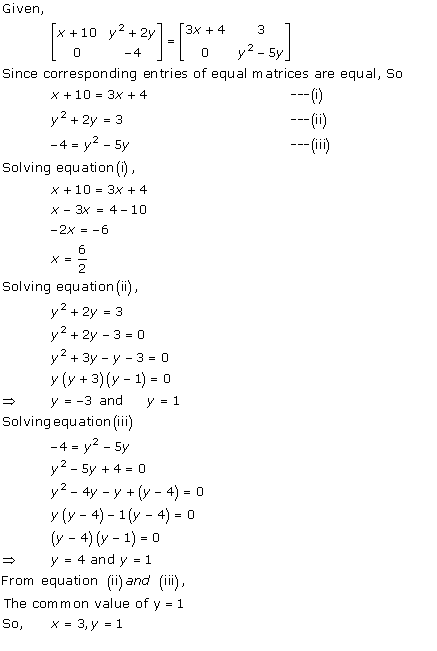
Solution 21
As A = B,
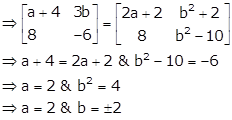
Algebra of Matrices Exercise Ex. 5.2
Solution 1
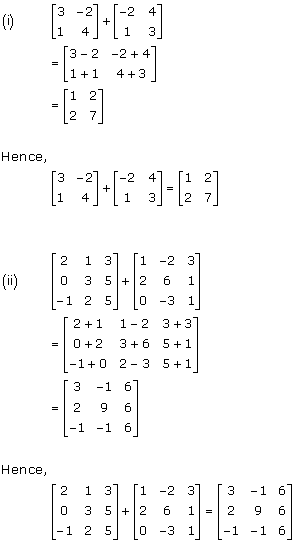
Solution 2(i)

Solution 2(ii)
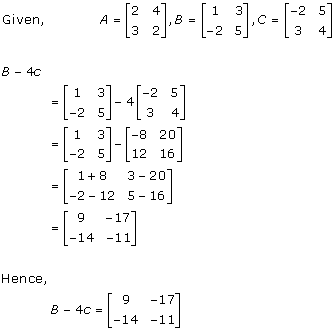
Solution 2(iii)

Solution 2(iv)
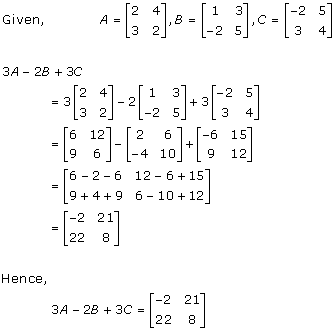
Solution 3

(ii)

Solution 4
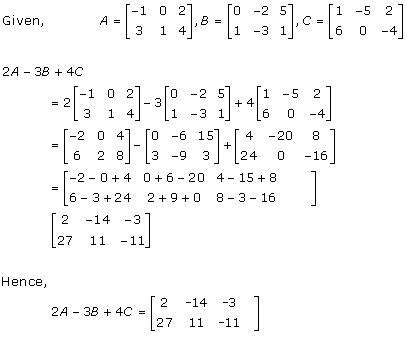
Solution 5
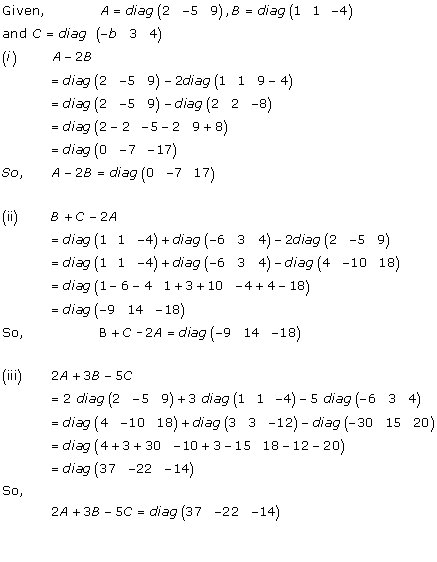
Solution 6

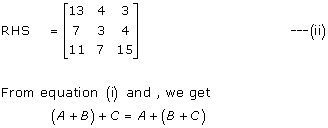
Solution 7
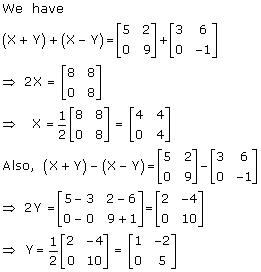
Solution 8
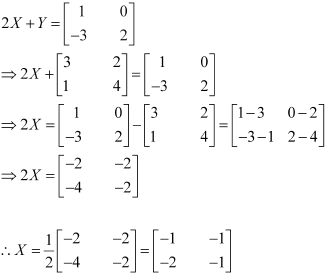
Solution 9

Solution 10
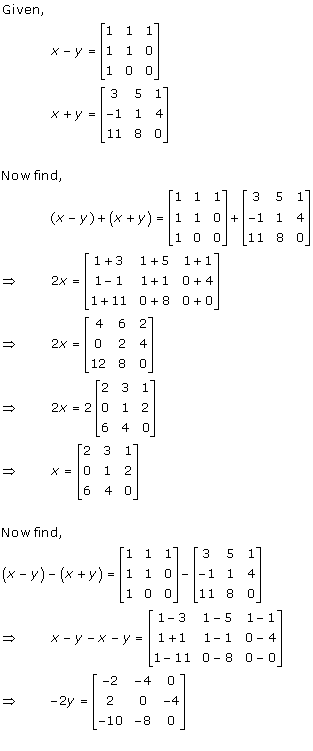
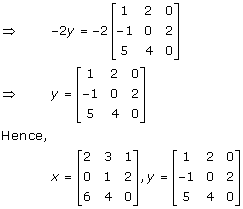
Solution 11
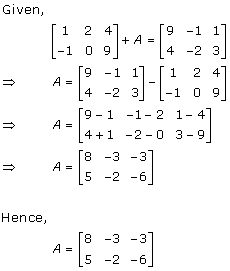
Solution 12
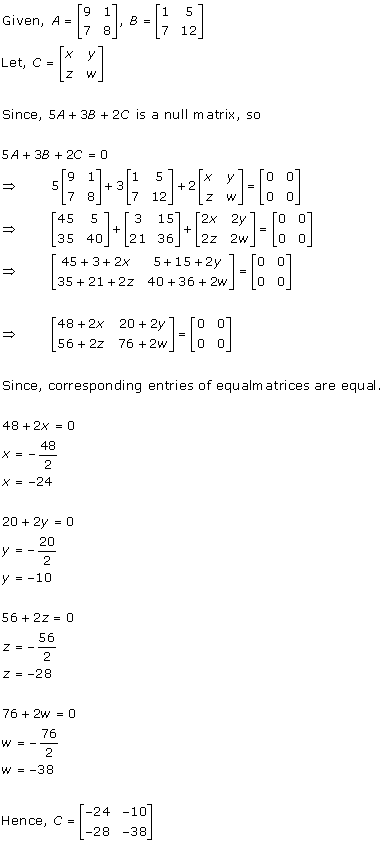
Solution 13
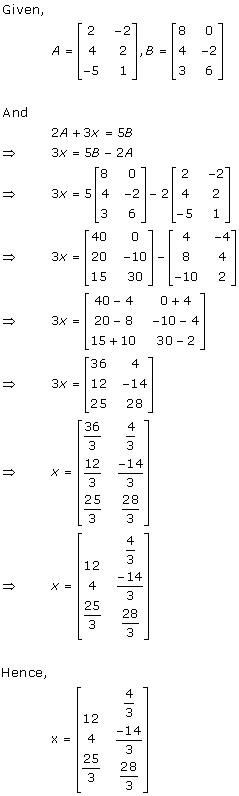
Solution 14
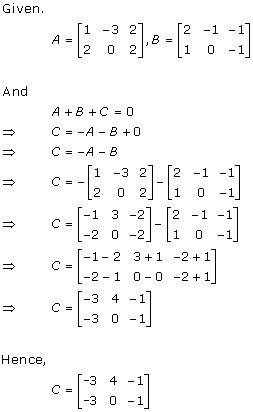
Solution 15(i)

Solution 15(ii)

Solution 15(iii)

Solution 16

Solution 17

Solution 18
(i)
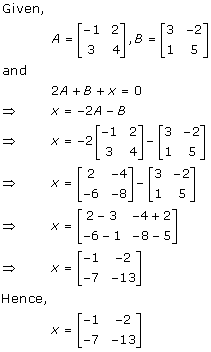
(ii)

Solution 19(i)

Solution 19(ii)
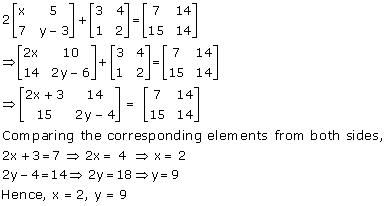
Solution 20

Solution 21

Solution 22
Let 3x and 4x be the monthly incomes of Aryan and Babban respectively.
Let 5y and 7y be their monthly expenditures respectively.
As each individual saves Rs. 15000 per month, we have
3x - 5y = 15000 … (i)
4x - 7y = 15000 … (ii)
The above equations can be written in matrix form as follows
![]()
Let AX = B, where
![]()
Let's find A-1
![]()
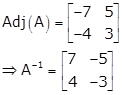
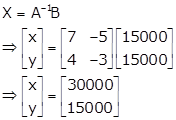
Therefore, x = Rs. 30000 and y = Rs. 15000
So, monthly income of Aryan = Rs. 90,000 and monthly income of Babban is Rs. 120,000.
Algebra of Matrices Exercise Ex. 5.3
Solution 1

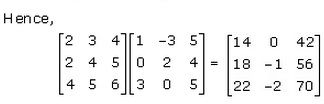
Solution 2(i)
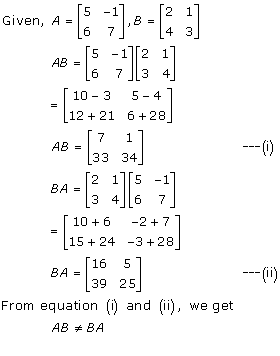
Solution 2(ii)
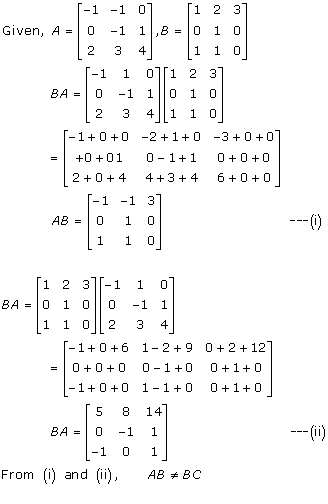
Solution 2(iii)
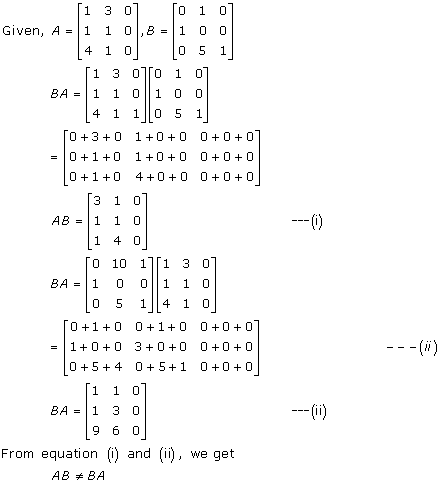
Solution 3(i)
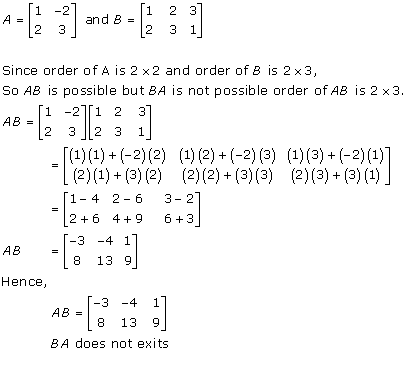
Solution 3(ii)

Solution 3(iii)

Solution 3(iv)
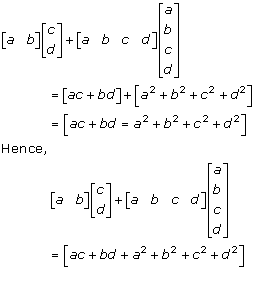
Solution 4(i)

Solution 4(ii)
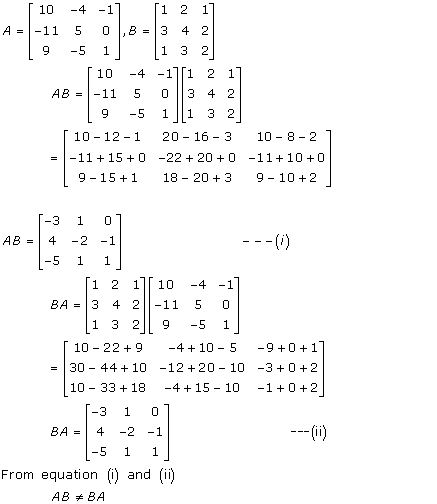
Solution 5(i)
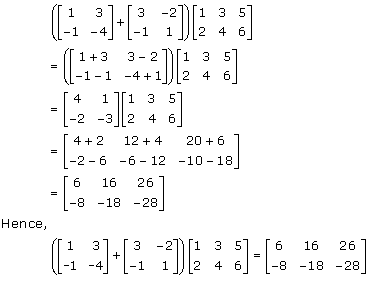
Solution 5(ii)
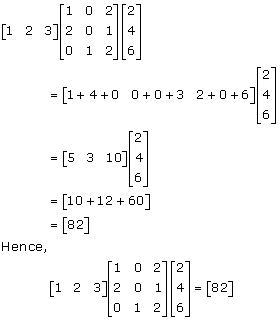
Solution 5(iii)

Solution 6
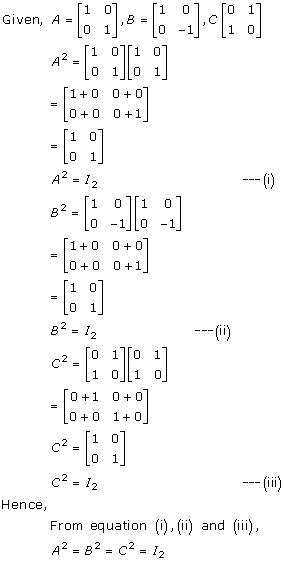
Solution 7

Solution 8
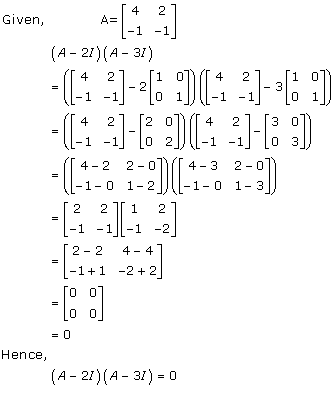
Solution 9
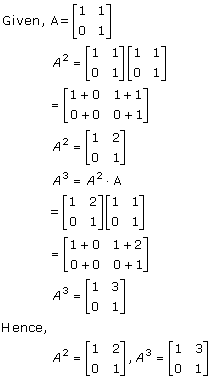
Solution 10
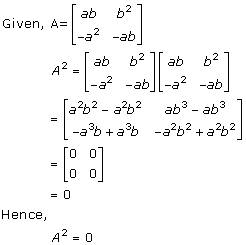
Solution 11

Solution 12
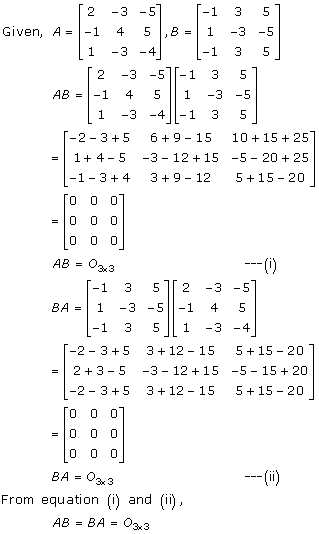
Solution 13

Solution 14

Solution 15

Solution 16(i)

Solution 16(ii)

Solution 17(i)
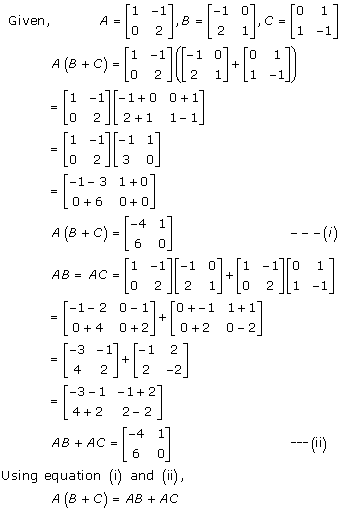
Solution 17(ii)

Solution 18

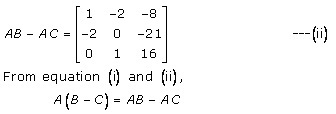
Solution 19

Solution 20

Solution 21

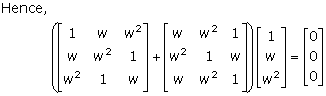
Solution 22

Solution 23
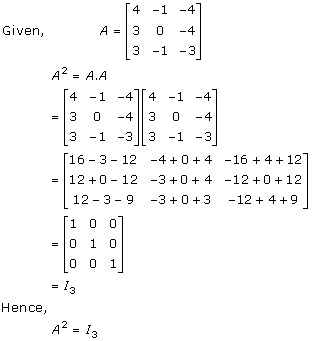
Solution 24(i)
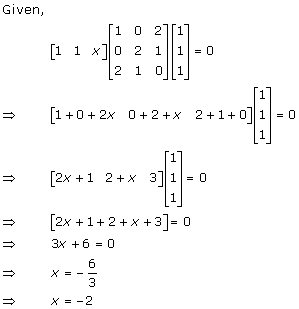
Solution 24(ii)

Solution 25
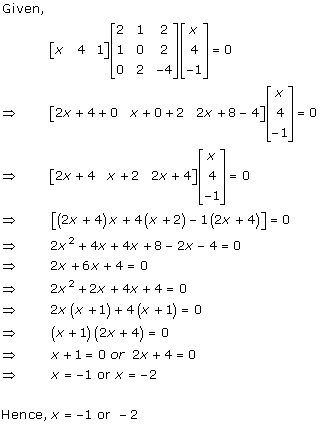
Solution 26
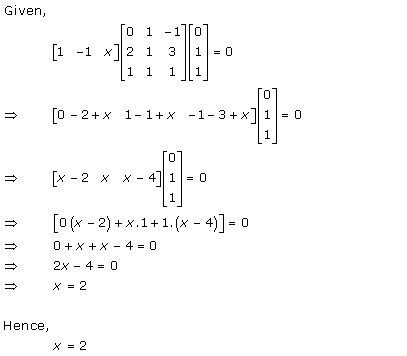
Solution 27
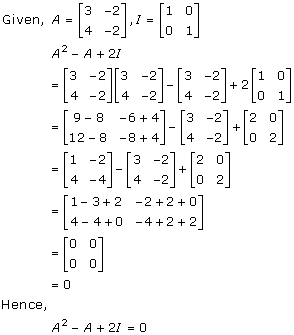
Solution 28

Solution 29
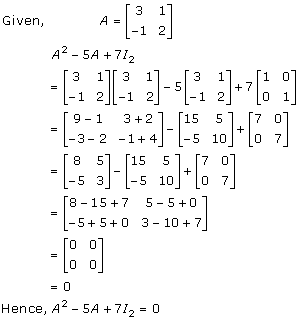
Solution 31
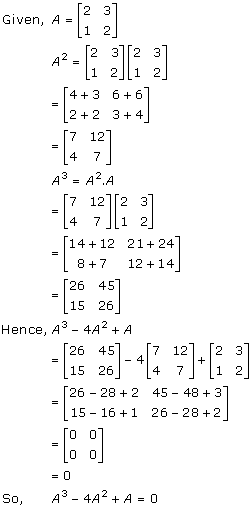
Solution 32

Solution 33
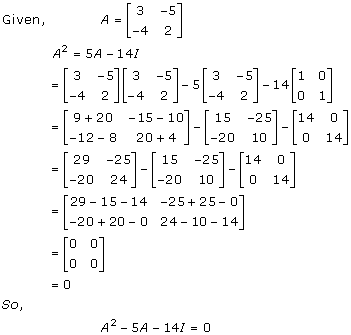
Solution 34


Solution 35
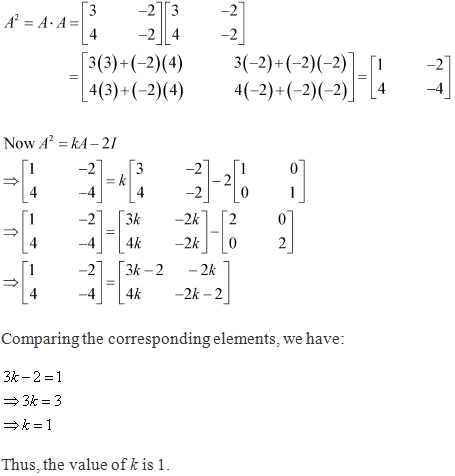
Solution 36

Solution 37
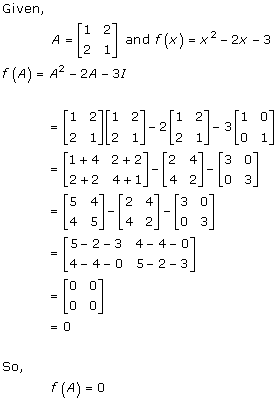
Solution 38
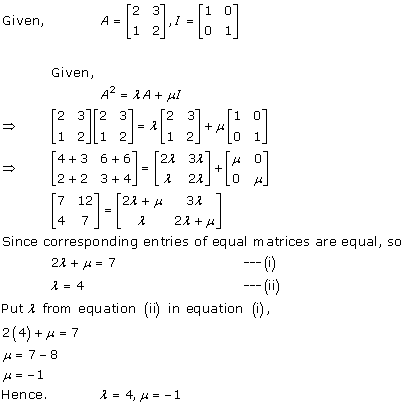
Solution 39

Solution 40(i)
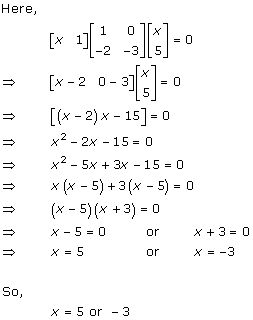
Solution 40(ii)
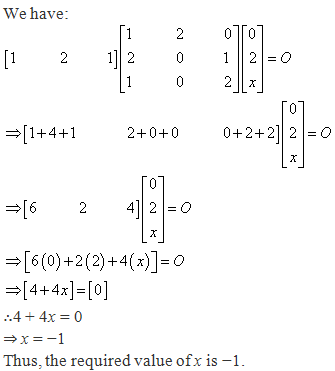
Solution 40(iii)
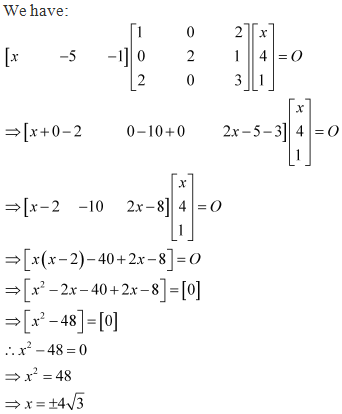
Solution 41

Solution 42
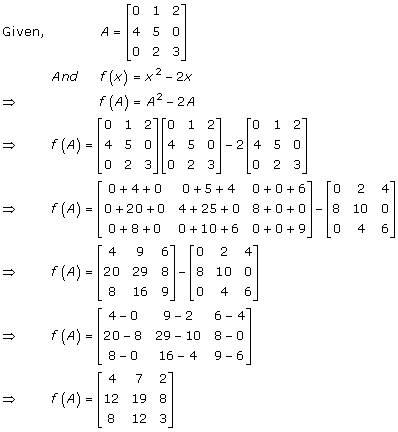
Solution 43
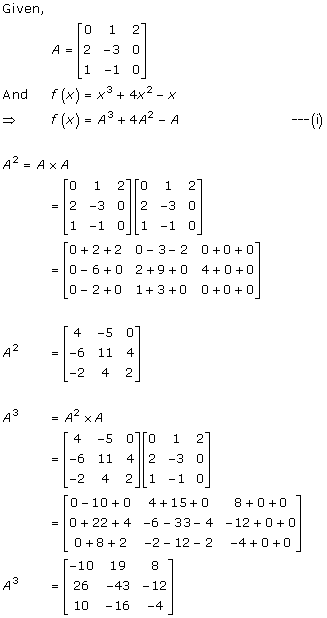
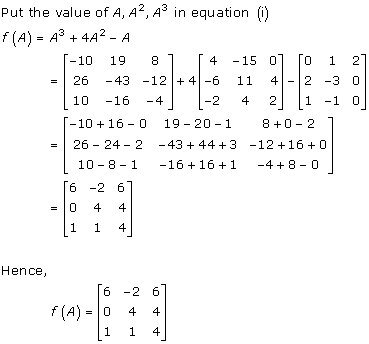
Solution 44

Solution 45

Solution 46

Solution 47

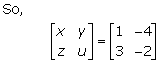
Solution 48(i)
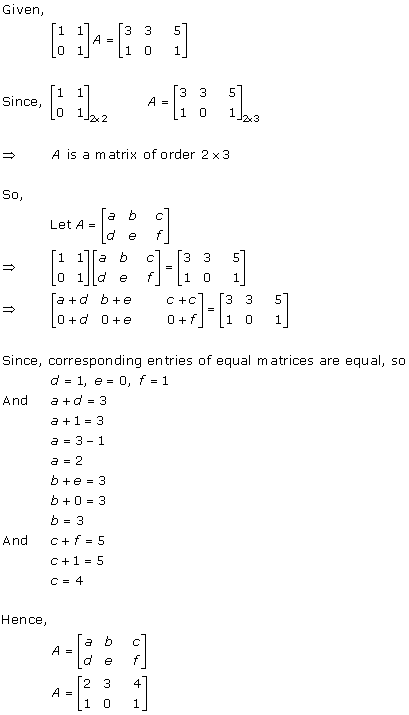
Solution 48(ii)
Solution 48(iii)

Solution 48(iv)

Solution 49
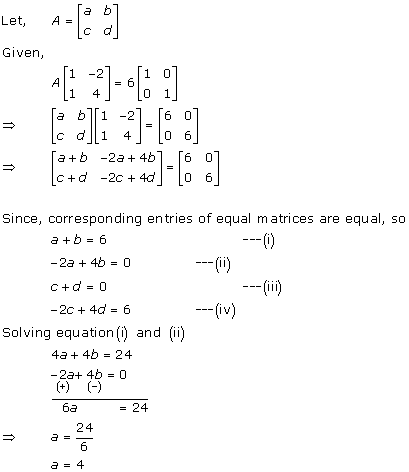
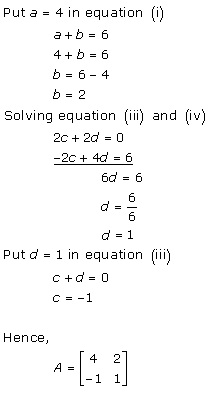
Solution 51
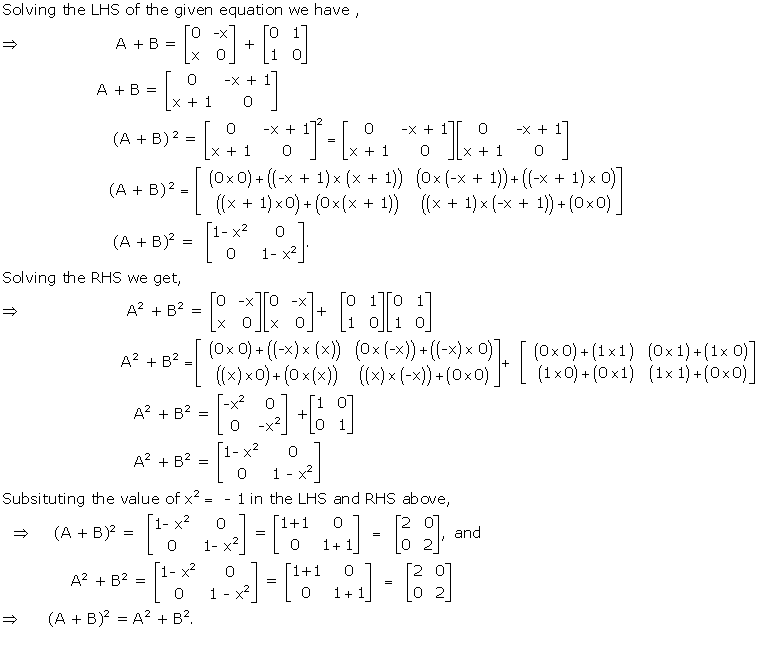
Solution 52
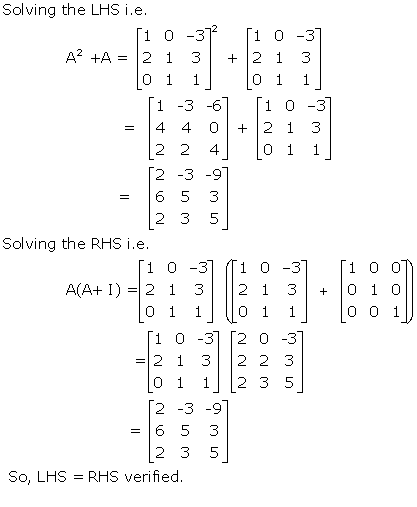
Solution 53
![]()

Solution 54(i)
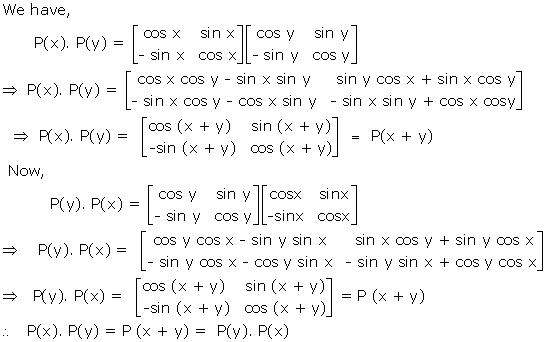
Solution 54(ii)

Solution 55

Solution 56

Solution 57


Solution 58

Solution 59

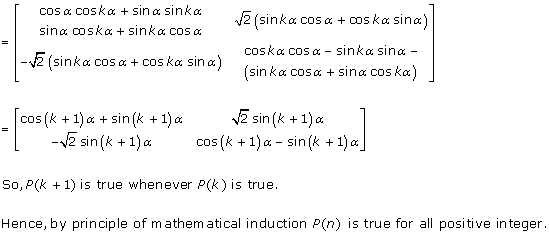
Solution 60


Solution 61

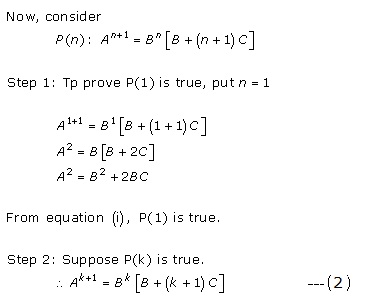

Solution 62


Solution 64
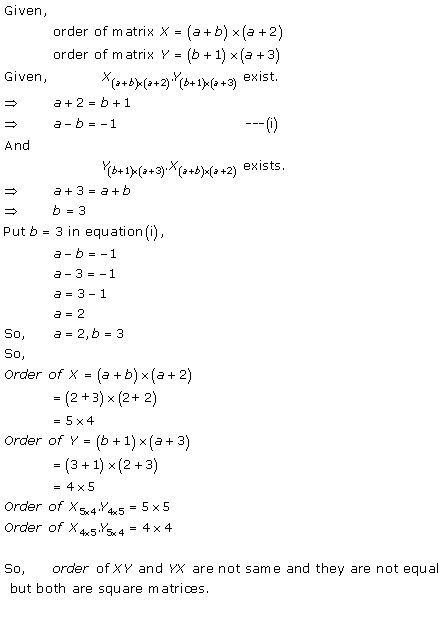
Solution 65(i)
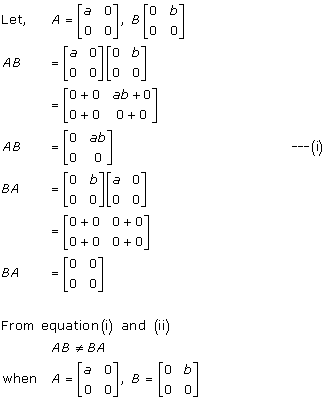
Solution 65(ii)
Solution 65(iii)
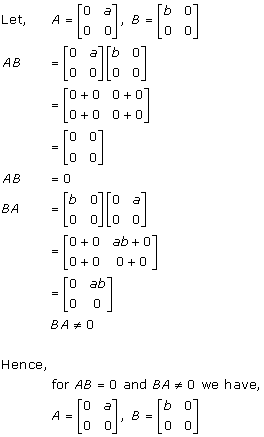
Solution 65(iv)
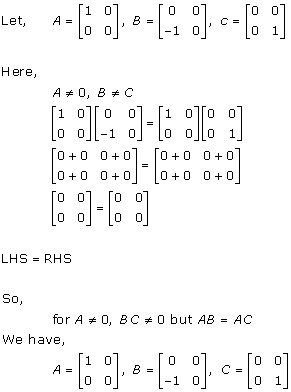
Solution 66

Solution 67

Solution 68


Solution 69

Solution 70

Solution 71

Solution 72

Solution 73

Solution 74


Solution 75

Solution 76

Solution 77

Solution 30
Given: A2 = A
(2 + A)3 - 19A
= 8I + A3 + 12A + 6A2 - 19A
= A3 + 6A2 - 7A + 8I
= A2 + 6A - 7A + 8I
= A - A + 8I
= 8I
Hence, (2 + A)3 - 19A = 8I.
Solution 40(iv)
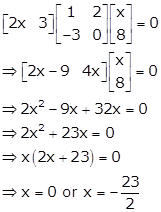
Solution 48(v)
Given: 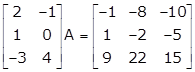
Let 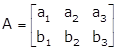
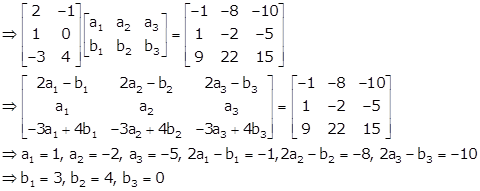
Hence, ![]()
Solution 48(vi)
Given: 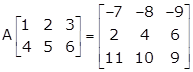
Let 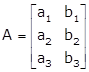
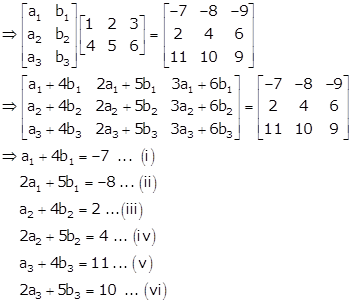
Solving equations (i) and (ii), we get, a1 = 1, b1 = -2
Solving (iii) and (iv), we get, a2 = 2, b2 = 0
From equations (v) and (vi), we get, a3 = -5, b3 = 4
Hence, 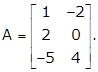
Solution 50
Given: ![]() and
and ![]()
As A2 + I = kA
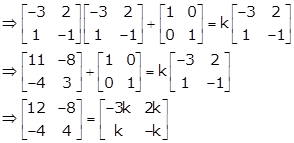
Hence, k = -4.
Solution 63
To prove ![]()
For n = 1,
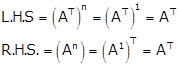
Therefore, it is true for n = 1.
Suppose the result is true for n = k
![]()
Take n = k + 1
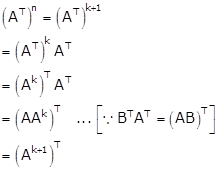
Thus, ![]() is true for
all n ∈ N.
is true for
all n ∈ N.
Solution 78
Let 3x and 4x be the monthly incomes of Aryan and Babbar respectively.
Let 5y and 7y be their monthly expenditures respectively.
As each individual saves Rs. 15000 per month, we have
3x - 5y = 15000 … (i)
4x - 7y = 15000 … (ii)
The above equations can be written in matrix form as follows
![]()
Let AX = B, where
![]()
Let's find A-1
![]()
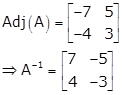
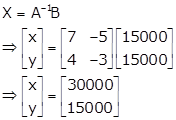
Therefore, x = Rs. 30000 and y = Rs. 15000
So, monthly income of Aryan = Rs. 90,000 and monthly income of Babbar is Rs. 120,000.
This encourages us to understand the power of savings and we should save certain money for future.
Solution 79
Let Rs. x and Rs. y is being invested in the first and second bonds respectively.
Let A be the investment matrix and B be the interest matrix.
Therefore, 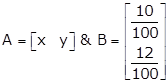
The annual
interest = AB = 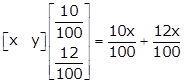
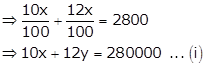
If the interest had been interchanged, the total interest would be Rs. 100 less.
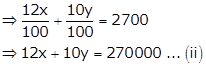
Equations (i) and (ii) can be expressed as
PX = Q, where ![]()
Now, |P| = 100 - 144 = -44
So, inverse of P exist.
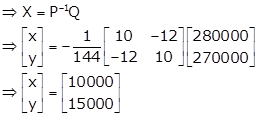
Thus, x = 10000 and y = 15000
Hence, the total amount invested is Rs. 25,000.
Algebra of Matrices Exercise Ex. 5.4
Solution 1(i)
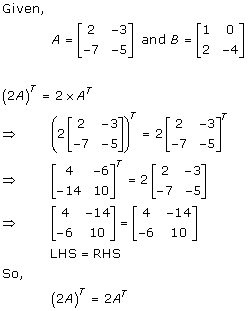
Solution 1(ii)
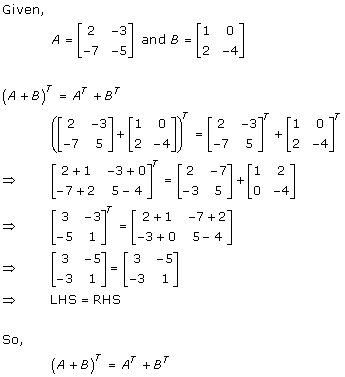
Solution 1(iii)
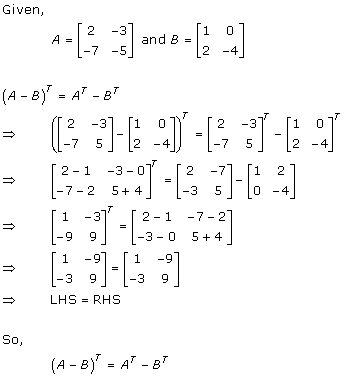
Solution 1(iv)
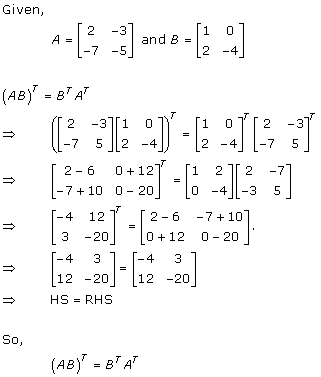
Solution 2
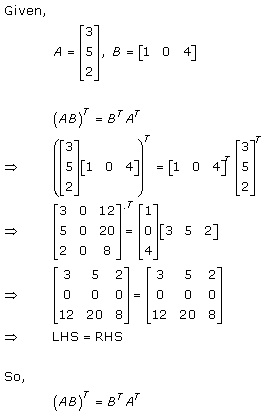
Solution 3(i)

Solution 3(ii)

Solution 3(iii)
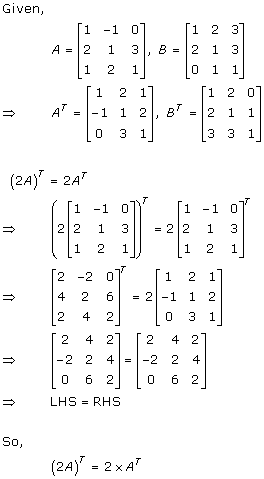
Solution 4

Solution 5
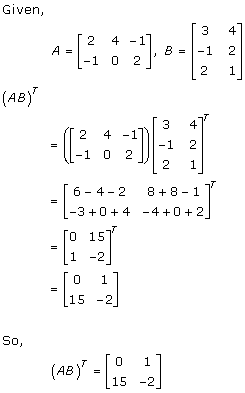
Solution 6(i)
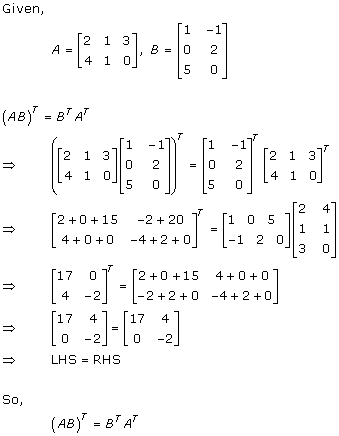
Solution 6(ii)
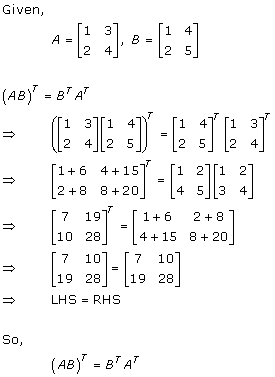
Solution 7

Solution 8

Solution 9
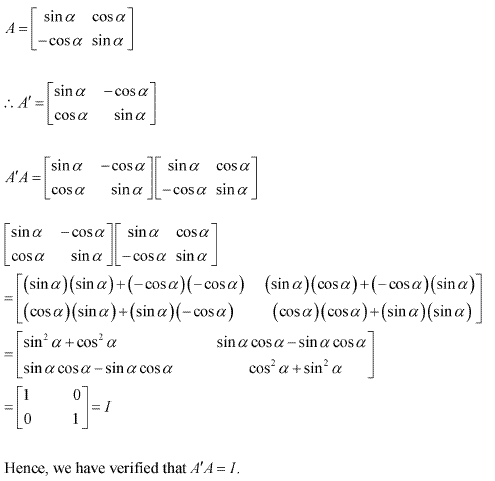
Solution 10

Algebra of Matrices Exercise Ex. 5.5
Solution 1

Solution 2

Solution 3
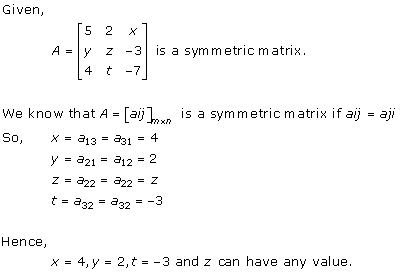
Solution 4

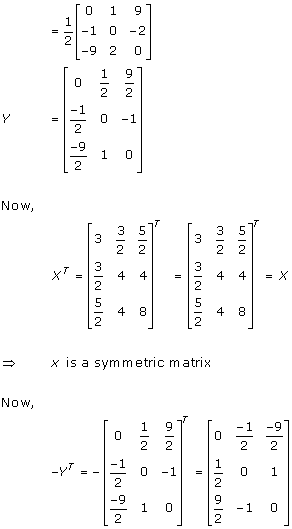
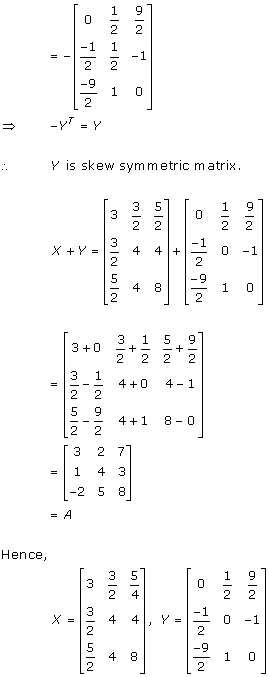
Solution 5



Solution 6
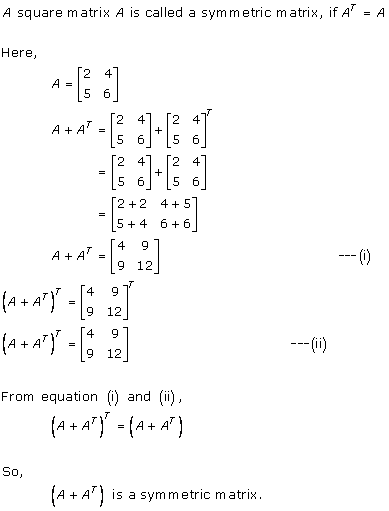
Solution 7

Solution 8


Solution 9
Given: ![]()
![]()
Consider,
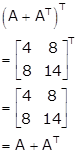
Thus, A + AT is a symmetric matrix.
Solution 10
As ![]() is a
symmetric matrix, its transpose will be equal to itself.
is a
symmetric matrix, its transpose will be equal to itself.
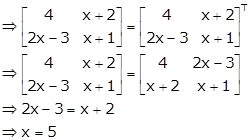
Hence, the value of x is 5.
Algebra of Matrices Exercise Ex. 5VSAQ
Solution 64
As A is a symmetric matrix, we have
AT = A
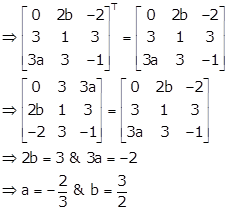
Solution 65
Number of elements in a 2 × 2 matrix = 4
The first element can be 1, 2 or 3.
The second element can be 1, 2 or 3.
Similarly, the remaining two elements can take either of the 3 numbers.
So, for every element we have 3 choices.
Therefore, number of ways of writing 1, 2 or 3 in a 2 × 2 matrix is 34 which is 81.
Thus, the number of all possible matrices of order 2 × 2 with each entry 1, 2 or 3 is 81.
Solution 66
Let 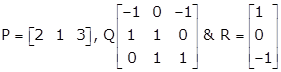
Order of matrix P is 1 × 3
Order of matrix Q is 3 × 3
Order of matrix R is 3 × 1
After multiplying P and Q, we'll get an output matrix B of order 1 × 3.
After multiplying B with R, we'll get an output matrix of order 1 × 1.
Hence, the order of matrix A is 1 × 1.
Solution 67
As P is
symmetric, we have ![]()
As Q is
skew-symmetric, we have ![]()
![]()
![]()
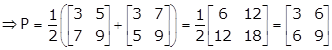
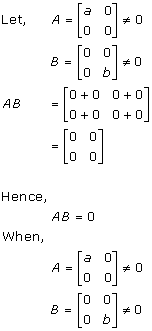
Solution 68
Matrix A is order 3 × 2
Matrix B is of order 2 × 4
Then the product matrix AB will have the order 3 × 4.
Solution 69
As matrix A is skew-symmetric
Therefore, -A = AT
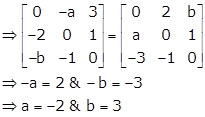
Hence, the values of a and b are -2 and 3 respectively.
Solution 1
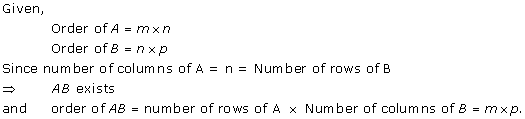
Solution 2

Solution 3
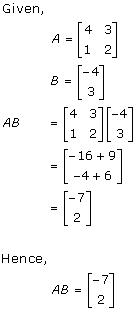
Solution 4
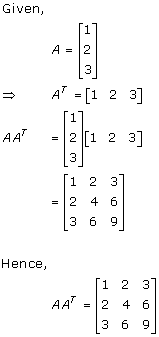
Solution 5
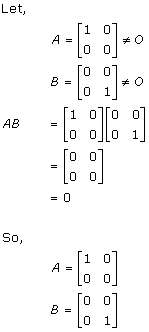
Solution 6
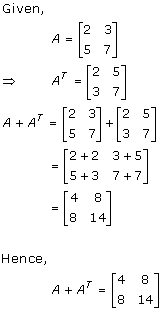
Solution 7

Solution 8
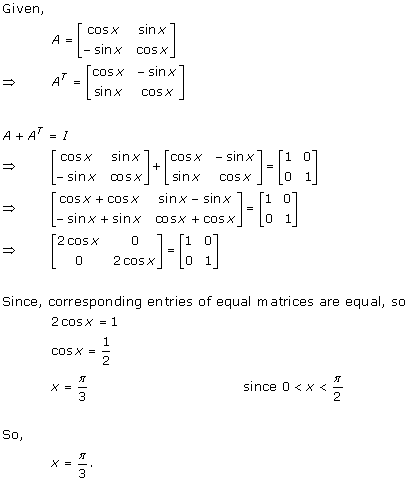
Solution 9
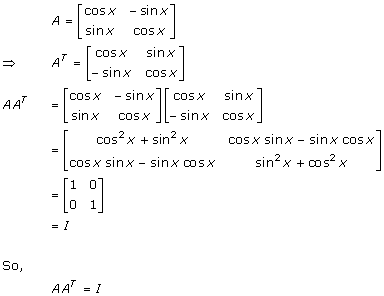
Solution 10
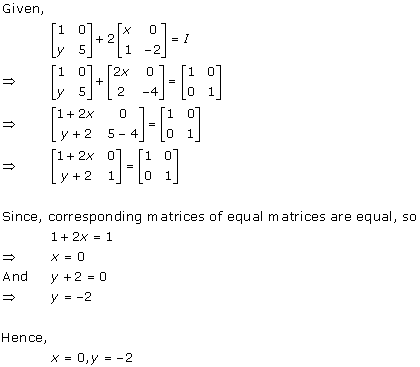
Solution 11

Solution 12

Solution 13
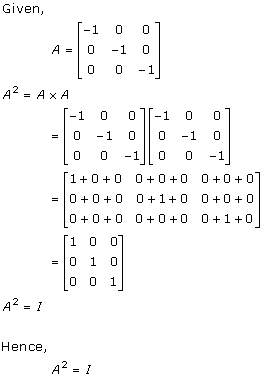

Solution 14

Solution 15
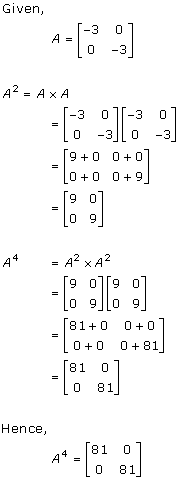
Solution 16
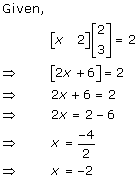
Solution 17
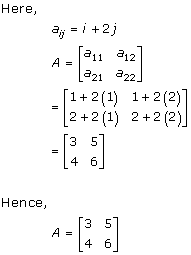
Solution 18
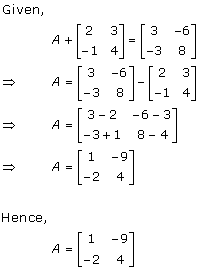
Solution 19
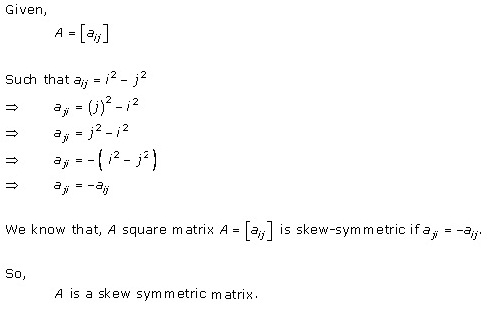
Solution 20
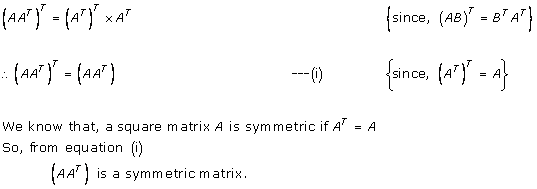
Solution 21
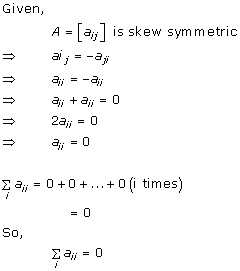
Solution 22
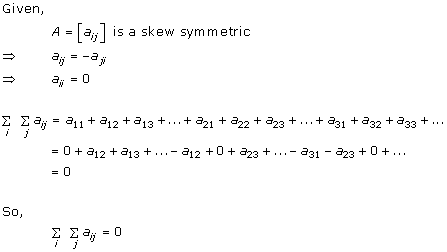
Solution 23

Solution 24

Solution 25

Solution 26

Solution 27
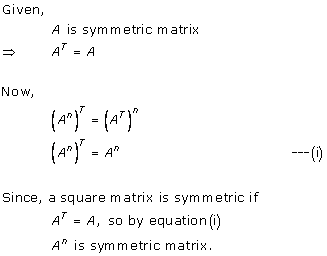
Solution 28

Solution 29

Solution 30

Solution 31

Solution 32
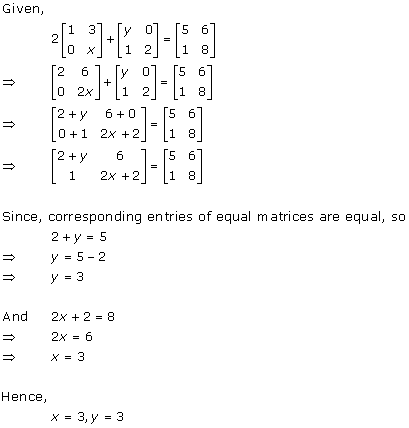
Solution 33
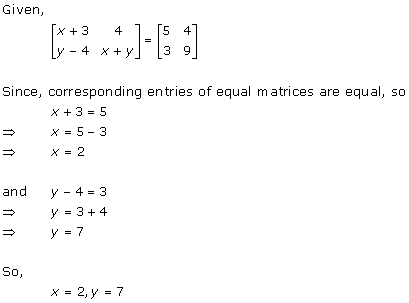
Solution 34
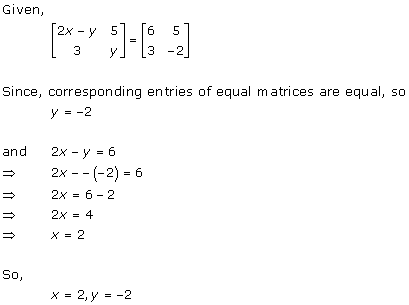
Solution 35
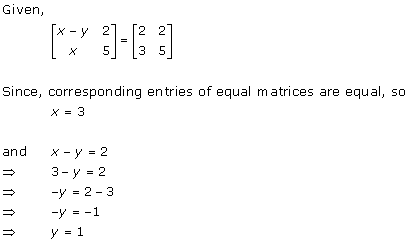
Solution 36
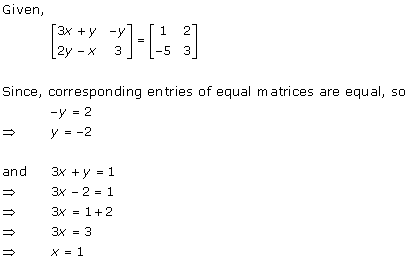
Solution 37
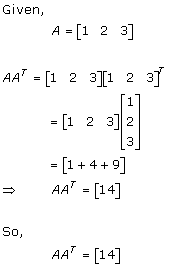
Solution 38
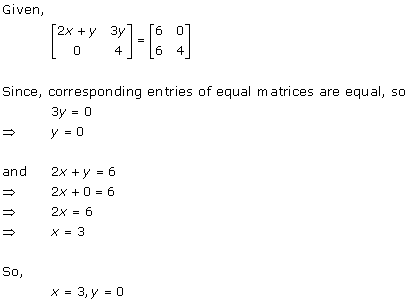
Solution 39
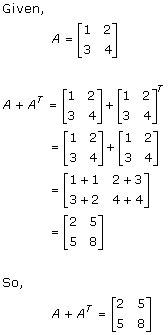
Solution 40

Solution 41
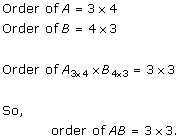
Solution 42
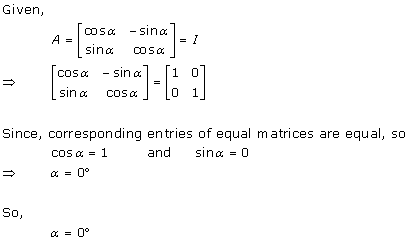
Solution 43
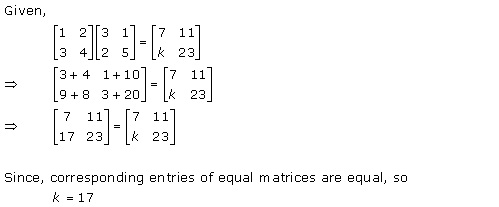
Solution 44

Solution 45
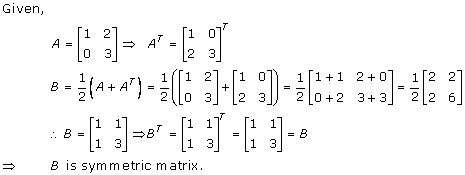
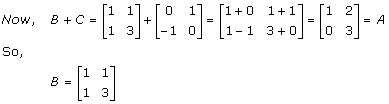
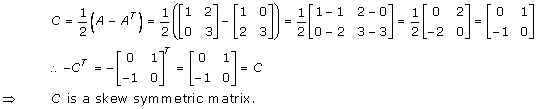
Solution 46

Solution 47

Solution 48

Solution 49
If a matrix is of order ![]() , then the number of elements in the matrix is the product
, then the number of elements in the matrix is the product ![]() .
.
Given that the required matrix is having 5 elements and 5 is a prime number.
Hence the prime factorization of 5 is either ![]() .
.
Thus, the order of the matrix is either ![]() .
.
Solution 50

Solution 51

Solution 52
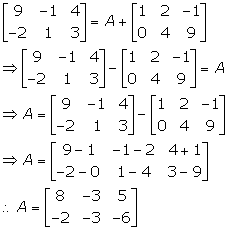
Solution 53
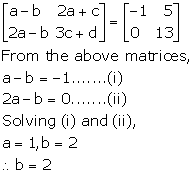
Solution 54

Solution 55
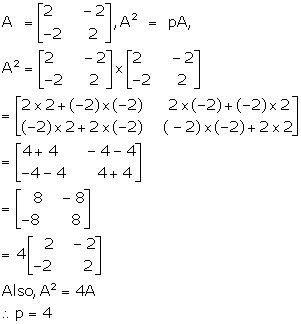
Solution 56
A2 = A
A3 = A2 = A
7A - (I + A)3
= 7A - (I3 + A3 + 3A2I + 3AI2)
= 7A - (I + A + 3A + 3A)
= 7A - (I + 7A)
= -I
Solution 57
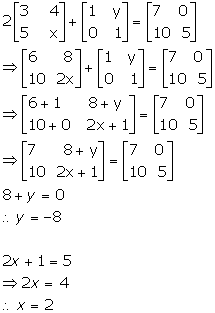
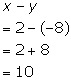
Solution 58
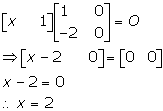
Solution 59
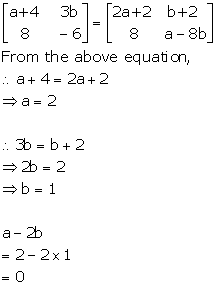
Solution 60
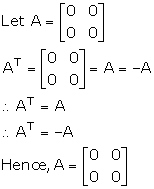
Solution 61
Solution 62

Solution 63