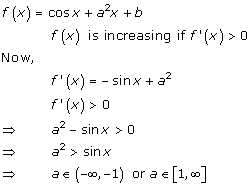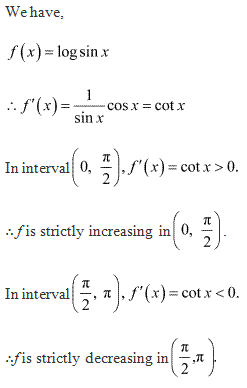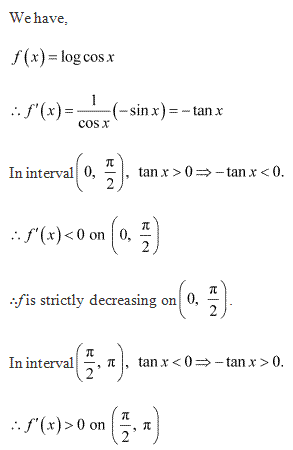Class 12-commerce RD SHARMA Solutions Maths Chapter 17: Increasing and Decreasing Functions
Increasing and Decreasing Functions Exercise MCQ
Solution 31
Given: ![]()
Differentiating w.r.t x, we get
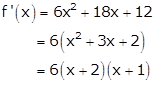
Take f'(x) = 0
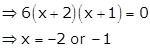
For x < -2,
x + 2 < 0 and x + 1 < 0
Therefore, f'(x) > 0
For -2 ≤ x ≤ -1,
x + 2 > 0 and x + 1 < 0
Therefore, f'(x) < 0
Hence, f(x) is decreasing in the interval [-2, -1].
Solution 32
Given: ![]()
Differentiating w.r.t x, we get
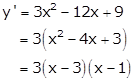
Take f'(x) = 0

For x < 1,
x - 3 < 0 and x - 1 < 0
Therefore, f'(x) > 0
For 1 < x < 3,
x - 3 < 0 and x - 1 > 0
Therefore, f'(x) < 0
For x > 3,
x - 3 > 0 and x - 1 > 0
So, f'(x) > 0
Hence, f(x) is decreasing for 1 < x < 3.
Solution 33
Given: ![]()
Differentiating w.r.t x, we get
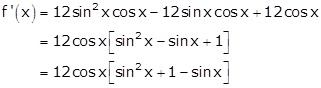
Now, ![]()
![]()
So, f'(x) > 0 when cos x > 0
i.e. ![]()
Therefore, f(x) is increasing when ![]()
Also, f'(x) < 0 when cos x < 0
i.e. ![]()
Therefore, f(x) is decreasing when ![]()
Hence, f(x) is decreasing in the interval ![]()
Solution 34
a. Let f(x) = sin 2x
Differentiating w.r.t x, we get
f'(x) = 2cos 2x
When ![]()
Now, ![]()
b. Let g(x) = tan x
Differentiating w.r.t x, we get
f'(x) = sec2x
Now, sec2x > 0 for ![]()
Therefore, f(x) is increasing in the interval ![]()
c. Let h(x) = cos x
Differentiating w.r.t x, we get
f'(x) = -sin x
Now, sin x > 0 for ![]()
So, -sin x < 0 for ![]()
Therefore, f(x) is decreasing in the interval ![]()
d. Let h(x) = cos 3x
Differentiating w.r.t x, we get
f'(x) = -3 sin 3x
When ![]()
Now, sin 3x > 0 for ![]()
Also, sin 3x < 0 for ![]()
Thus, cos x is decreasing in the interval ![]()
Solution 35
Given: f(x) = tan x - x
Differentiating w.r.t x, we get
f'(x) = sec2x - 1 = tan2x
Now, tan2x ≥ 0
Hence, f(x) always increases.
Solution 1
Correct option: (b)

Solution 2
Correct option: (c)

Solution 3
Correct option: (c)

Solution 4
Correct option:(b)

Solution 5
Correct option: (a)

Solution 6
Correct option: (c)

Solution 7
Correct option: (b)

Solution 8
Correct option: (c)

Solution 9
Correct option: (a)
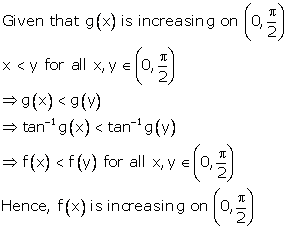
Solution 10
Correct option: (c)

Solution 11
Correct option: (b)

Solution 12
Correct option: (a)
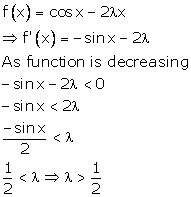
Solution 13
Correct option: (b)

Solution 14
Correct option: (d)

Solution 15
Correct option: (d)
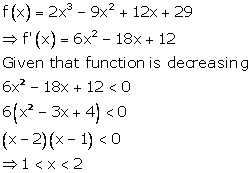
Solution 16
Correct option: (c)
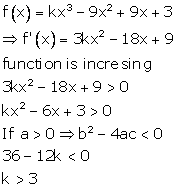
Solution 17
Correct option: (c)

Solution 18
Correct option: (d)

Solution 19
Correct option: (a)
Every invertible function is always monotonic function.
Solution 20
Correct option: (b)

Solution 21
Correct option: (c)

Solution 22
Correct option: (a)

Solution 23
Correct option: (d)

Solution 24
Correct option: (d)

Solution 25
Correct option: (b)

Solution 26
Correct option: (b)

Solution 27
Correct option: (d)

Solution 28
Correct option: (a)

Solution 29
Correct option: (a)

NOTE: Option (a) should be -1 < k < 1.
Solution 30
Correct option: (a)
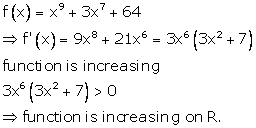
Increasing and Decreasing Functions Exercise Ex. 17.1
Solution 1
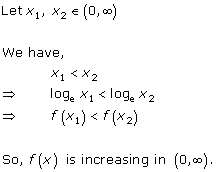
Solution 2
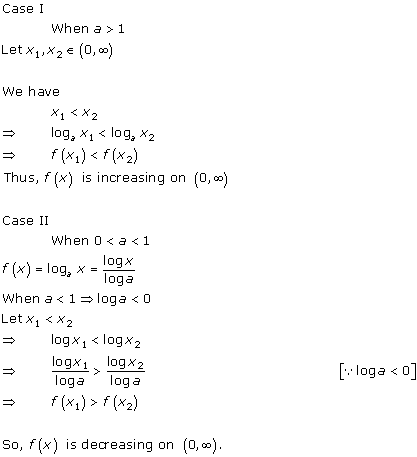
Solution 3

Solution 4
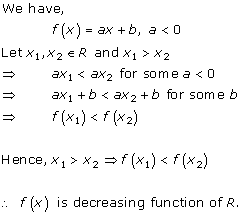
Solution 5
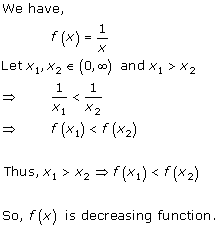
Solution 6
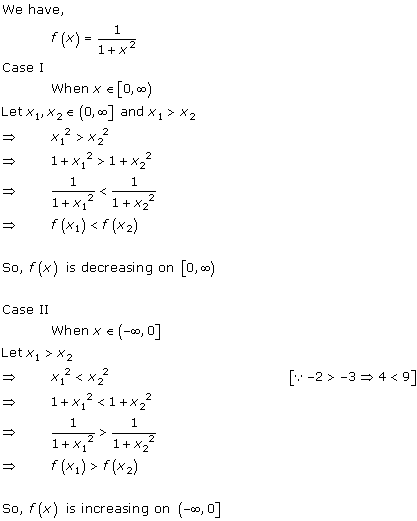
Solution 7

Solution 8
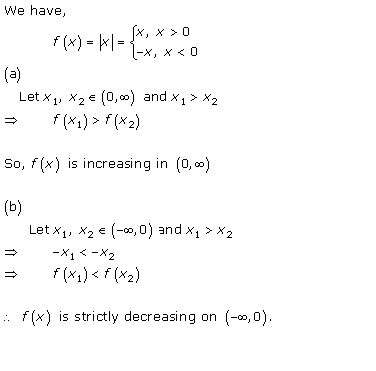
Solution 9
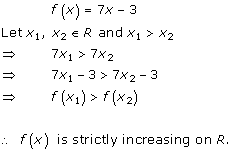
Increasing and Decreasing Functions Exercise Ex. 17.2
Solution 1(i)
Solution 1(ii)
Solution 1(iii)
Solution 1(iv)

Solution 1(v)

Solution 1(vi)

Solution 1(vii)

Solution 1(viii)

Solution 1(ix)

Solution 1(xi)

Solution 1(xii)

Solution 1(xiii)
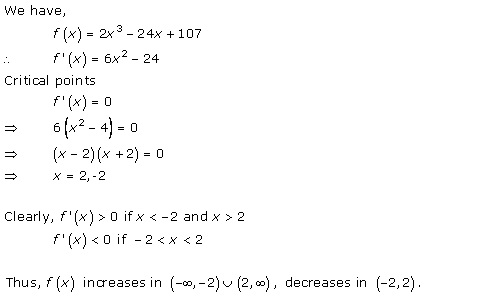
Solution 1(xiv)
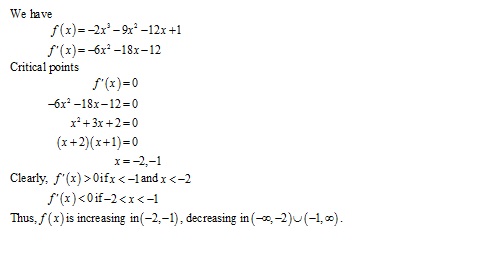
Solution 1(xv)

Solution 1(xvi)

Solution 1(xvii)
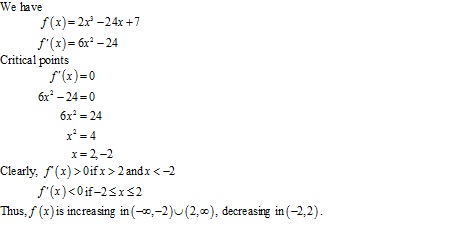
Solution 1(xviii)

Solution 1(xix)

Solution 1(xx)

Solution 1(xxi)

Solution 1(xxii)

Solution 1(xxiii)

Solution 1(xxiv)

Solution 1(xxv)
Solution 1(xxvi)

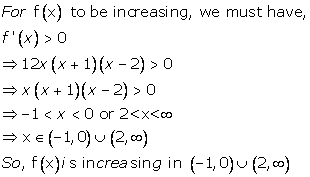
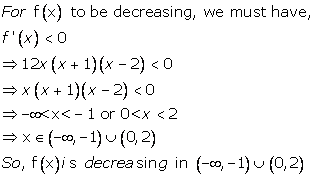
Solution 1(xxvii)



Solution 1(xxviii)



Solution 2

Solution 3
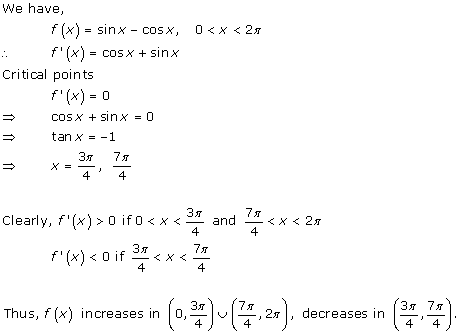
Solution 4

Solution 5

Solution 6

Solution 7
Solution 8
Solution 9
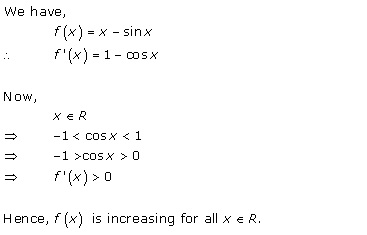
Solution 10

Solution 11

Solution 12

Solution 13

Solution 14
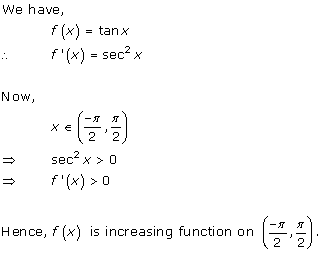
Solution 15
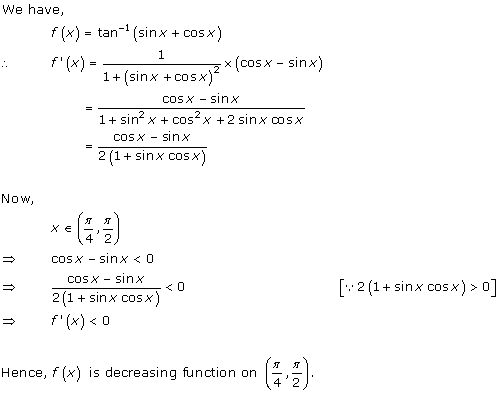
Solution 16
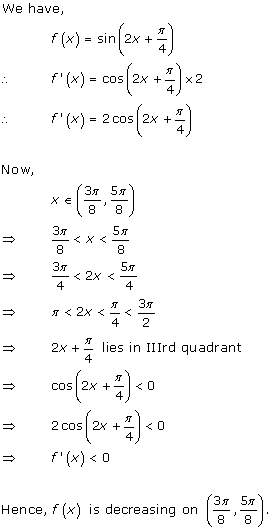
Solution 17
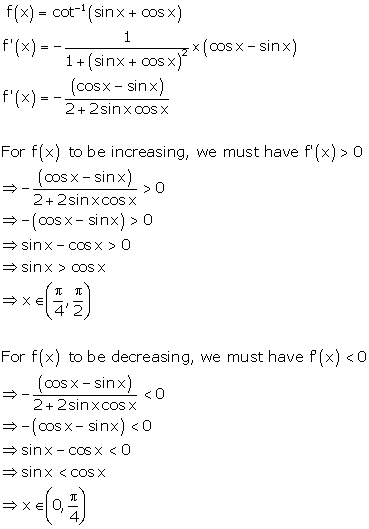
Solution 18

Solution 19
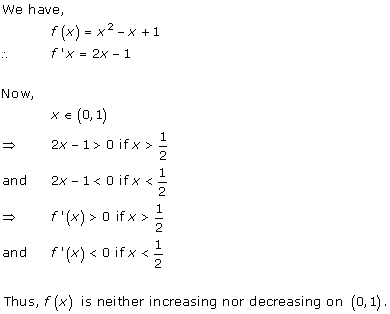
Solution 20

Solution 21

Solution 22

Solution 23
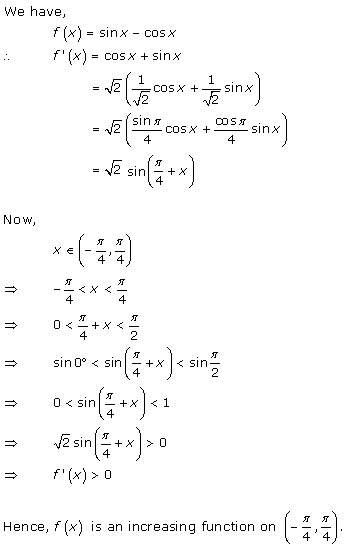
Solution 24
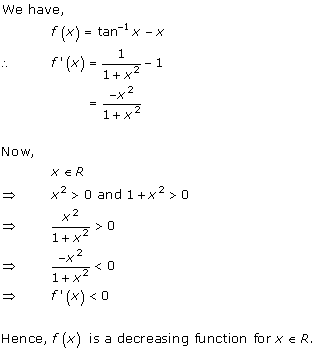
Solution 25

Solution 26

Solution 27

Solution 28

Solution 29

Solution 30(i)

Solution 31
Solution 32
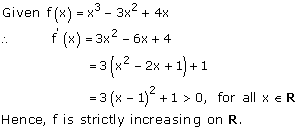
Solution 33
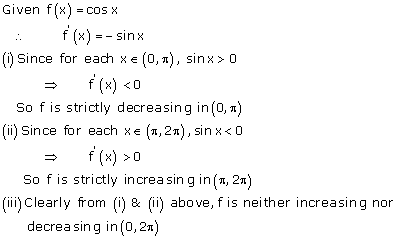
Solution 34
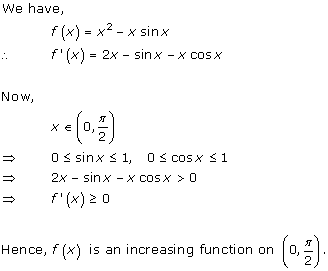
Solution 35

Solution 36
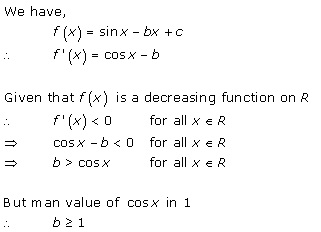
Solution 37
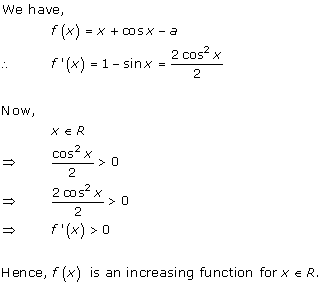
Solution 38

Solution 39(i)

Solution 39(ii)

Solution 39(iii)



Solution 1(x)
Given: ![]()
Differentiating w.r.t x, we get
![]()
Take f'(x) = 0
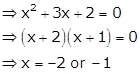
Clearly, f'(x) > 0 if x < -2 or x > -1
And, f'(x) < 0 if -2 < x < -1
Thus, f(x)
increases on ![]() and decreases
on
and decreases
on ![]()
Solution 1(xxix)
Given: ![]()
Differentiating w.r.t x, we get
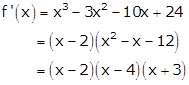
Take f'(x) = 0
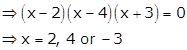
The points x = 2,
4 and -3 divide the number line into four disjoint intervals namely ![]()
Consider the
interval ![]()
In this case, x - 2 < 0, x - 4 < 0 and x + 3 < 0
Therefore, f'(x)
< 0 when ![]()
Thus the function
is decreasing in ![]()
Consider the
interval ![]()
In this case, x - 2 < 0, x - 4 < 0 and x + 3 > 0
Therefore, f'(x)
> 0 when ![]()
Thus the function
is increasing in ![]()
Now, consider the
interval ![]()
In this case, x - 2 > 0, x - 4 < 0 and x + 3 > 0
Therefore, f'(x)
< 0 when ![]()
Thus the function
is decreasing in ![]()
And now, consider
the interval ![]()
In this case, x - 2 > 0, x - 4 > 0 and x + 3 > 0
Therefore, f'(x)
< 0 when ![]()
Thus the function
is increasing in ![]()
Solution 30(ii)
Given: ![]()
Differentiating w.r.t x, we get
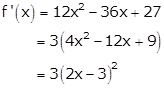
Now, ![]()
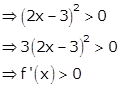
Hence, f(x) is an increasing function for all x.
Increasing and Decreasing Functions Exercise Ex.17VSAQ
Solution 1
![]()
Solution 2
![]()
Solution 3
![]()
Solution 4
![]()
Solution 5
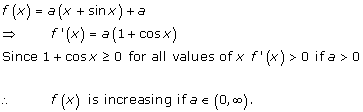
Solution 6
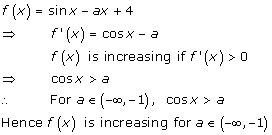
Solution 7
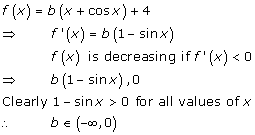
Solution 8

Solution 9
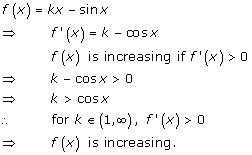
Solution 10
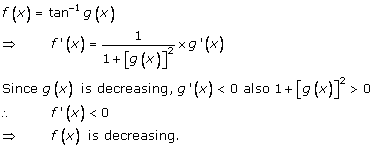
Solution 11
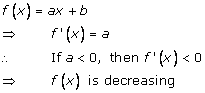
Solution 12
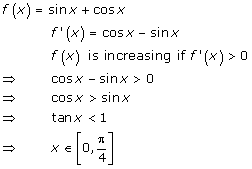
Solution 13
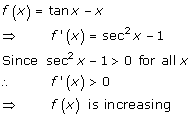
Solution 14