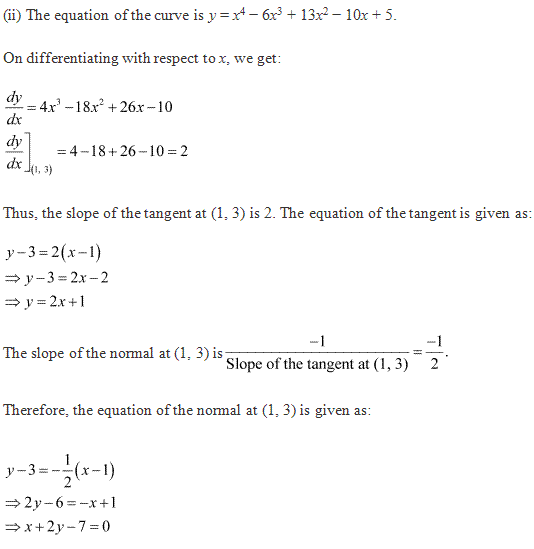Class 12-commerce RD SHARMA Solutions Maths Chapter 16 - Tangents and Normals
Tangents and Normals Exercise MCQ
Solution 30
Let (p, q) be the
point on the given curve 
at which the
normal passes through the origin.
Therefore, 
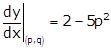
Now, the equation of normal at (p, q) is passing through origin.
Therefore,
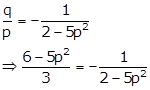
As p = 1 satisfies the equation, therefore the abscissa is 1.
Solution 31
The curves are
… (i)
… (ii)
Differentiating (i) w.r.t x, we get
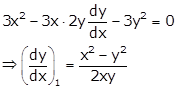
Differentiating (ii) w.r.t x, we get
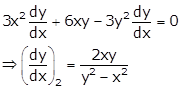
Now, 
So, both the curves are cut each other at right angle.
Solution 32
Given: 
Differentiating 'x' and 'y' w.r.t t, we get
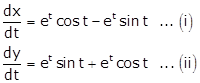
Dividing (ii) by (i), we get
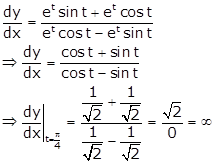
Hence, the
tangent to the curve makes an angle of 
with x-axis.
Solution 33
Given curve is 
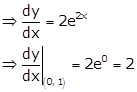
Therefore, slope of tangent is 2.
The equation of tangent is y - 1 = 2(x - 0)
i.e. y = 2x + 1
This equation of tangent meets x-axis when y = 0
Thus, the
required point is 
Solution 34
Given curve is 
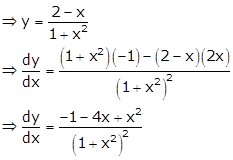
The curve crosses x-axis when y = 0
Therefore, x = 2
So, the tangent touches the curve at point (2, 0).
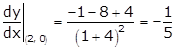
The equation of tangent at (2, 0) is
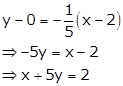
Solution 35
Given curve is 
As the tangents are parallel to x-axis, their slope will be 0.
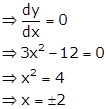
When x = 2, y = 23 - 12 × 2 + 18 = 2
When x = -2, y = (-2)3 - 12(-2) + 18 = 34
So, the points are (2, 2) and (-2, 34).
Solution 36
Given curve is 
At (0, 0), we have
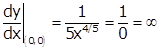
Thus, the given
curve has vertical
tangent, which is parallel to y-axis, at (0, 0).
Solution 1
Correct option: (c)
Solution 2
Correct option: (d)
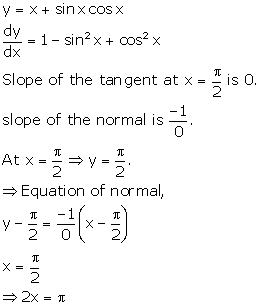
Solution 3
Correct option: (a)
Solution 4
Correct option: (b)
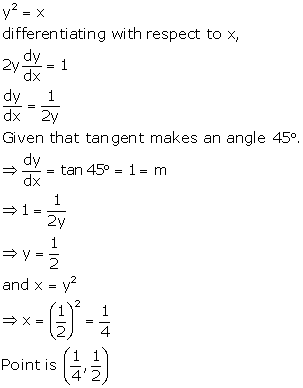
Solution 5
Correct option: (c)
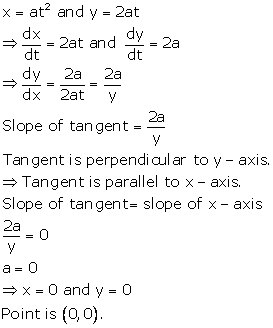
Solution 6
Correct option: (b)
Solution 7
Correct option:(b)
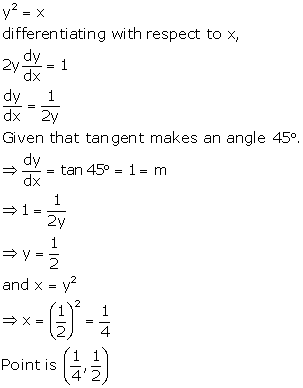
Solution 8
Correct option: (d)
Solution 9
Correct option: (b)
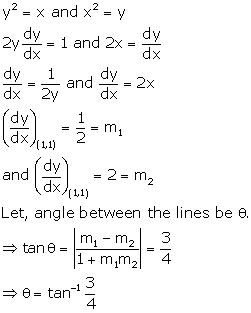
Solution 10
Correct option: (c)
Solution 11
Correct option: (b)
Solution 12
Correct option: (b)
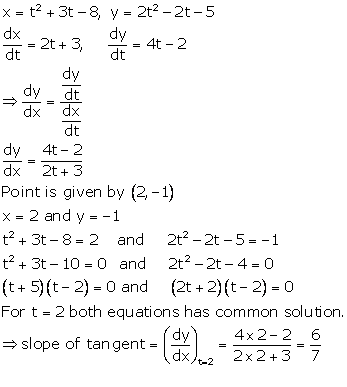
Solution 13
Correct option: (d)
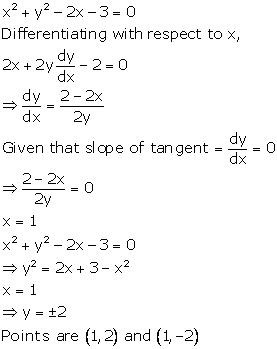
Solution 14
Correct option: (c)
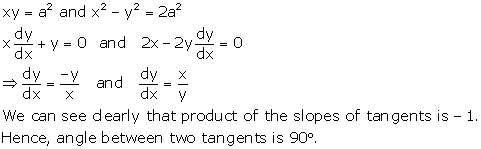
Solution 15
Correct option: (c)
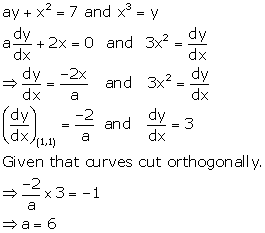
Solution 16
Correct option: (b)
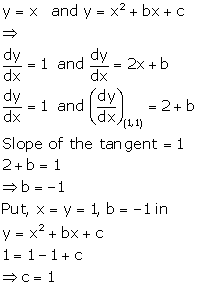
Solution 17
Correct option: (b)
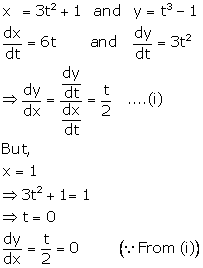
Solution 18
Correct option: (c)
Solution 19
Correct option: (c)
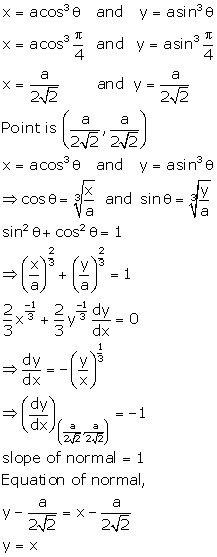
Solution 20
Correct option: (a)
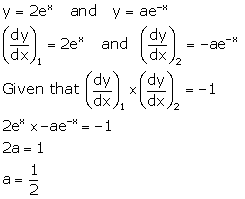
Solution 21
Correct option: (b)
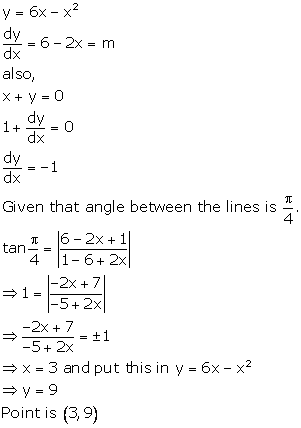
Solution 22
Correct option: (c)
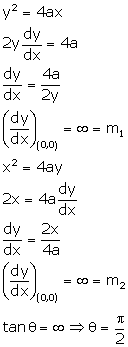
Solution 23
Correct option: (c)
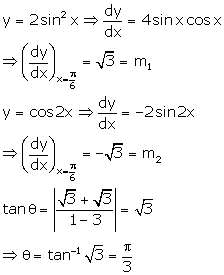
Solution 24
Correct option: (c)
Solution 25
Correct option: (a)
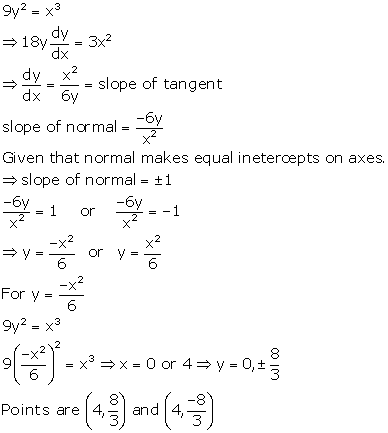
Solution 26
Correct option: (b)
Solution 27
Correct option: (a)
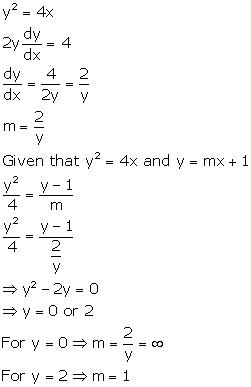
Solution 28
Correct option: (b)
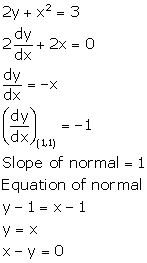
Solution 29
NOTE: Options are incorrect.
Tangents and Normals Exercise Ex. 16.1
Solution 1(i)
Solution 1(ii)
Solution 1(iii)
Solution 1(iv)
Solution 1(v)
Solution 1(vi)
Solution 1(vii)
Solution 1(viii)
Solution 1(ix)
Solution 1(x)
Solution 2
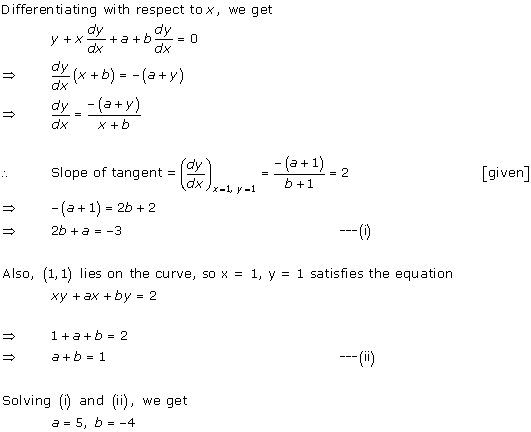
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
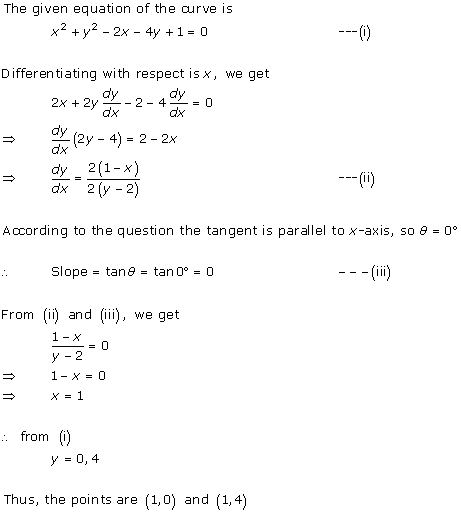
Solution 10
Solution 11
Solution 12
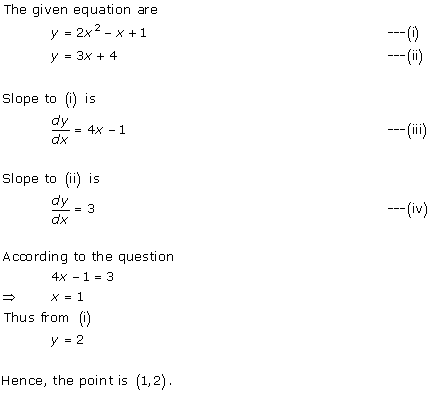
Solution 13
Solution 14
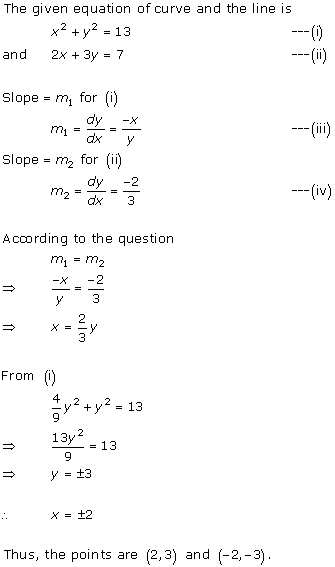
Solution 15
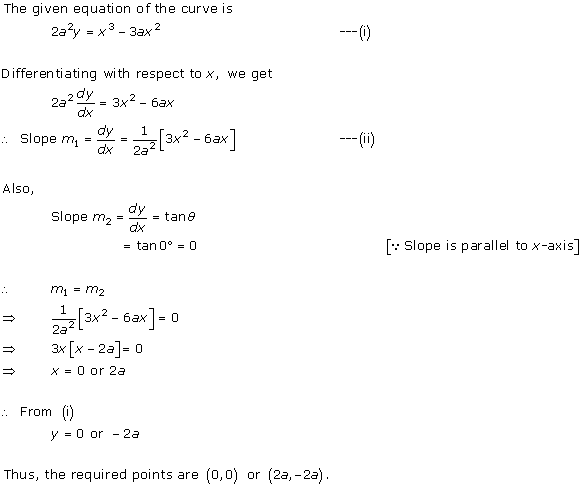
Solution 16
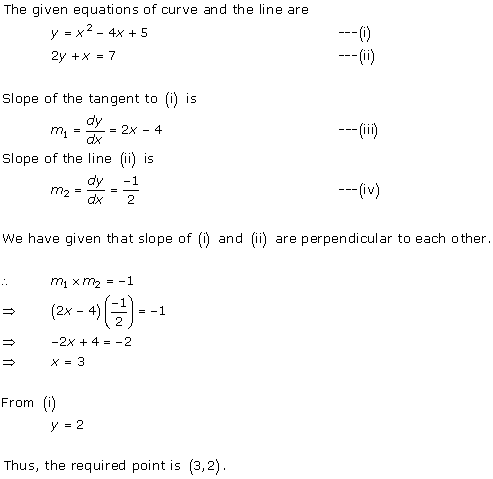
Solution 17
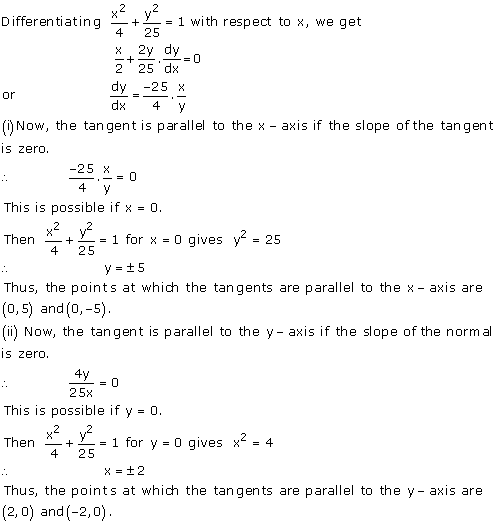
Solution 18
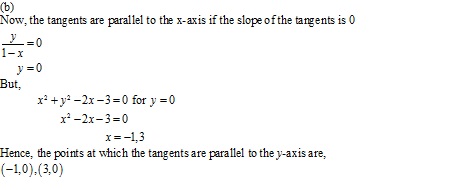
Solution 19
Solution 20
Solution 21
Tangents and Normals Exercise Ex. 16.2
Solution 1
Solution 2
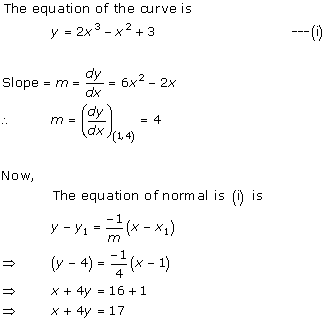
Solution 3(i)
Solution 3(ii)
Solution 3(iii)
Solution 3(iv)
Solution 3(v)
Solution 3(vi)
Solution 3(vii)
Solution 3(viii)
Solution 3(ix)
Solution 3(x)
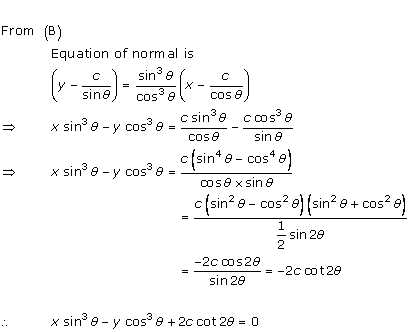
Solution 3(xi)
Solution 3(xii)
Solution 3(xiii)
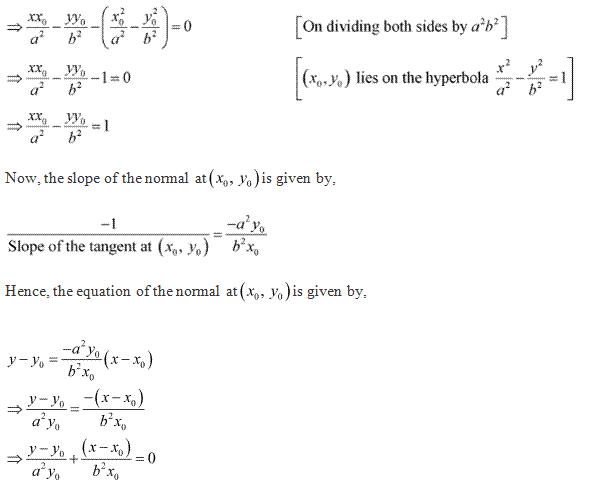
Solution 3(xiv)
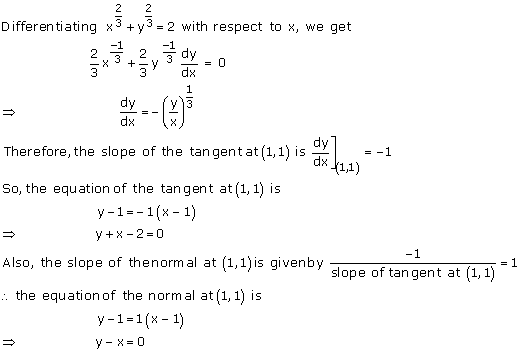
Solution 3(xv)
Solution 3(xvi)
The equation of the given curve is y2 = 4x . Differentiating with respect to x, we have:
Solution 3(xix)
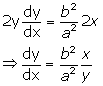
Solution 4
Solution 5(i)
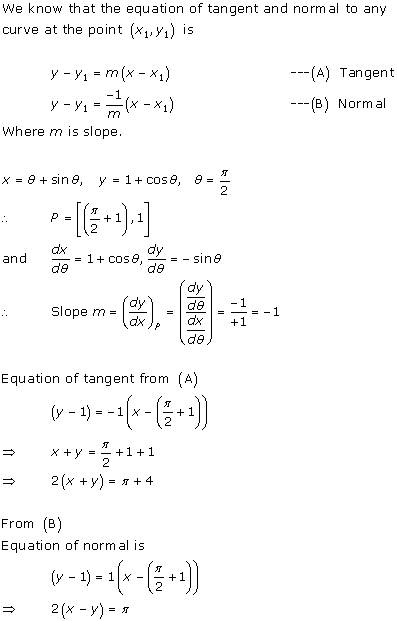
Solution 5(ii)
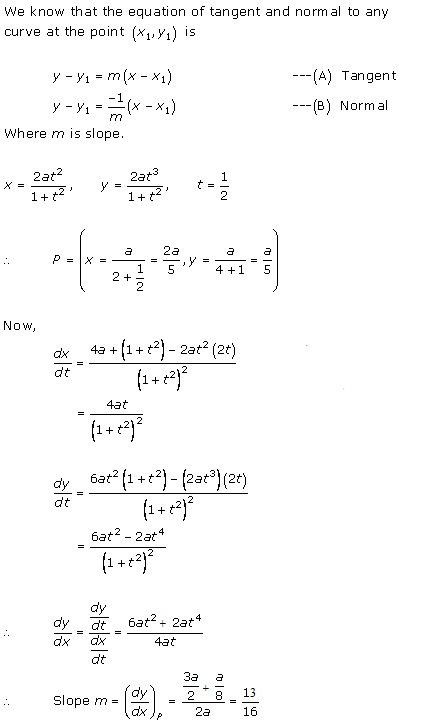
From (A)
Equation of tangent is
Solution 5(iii)
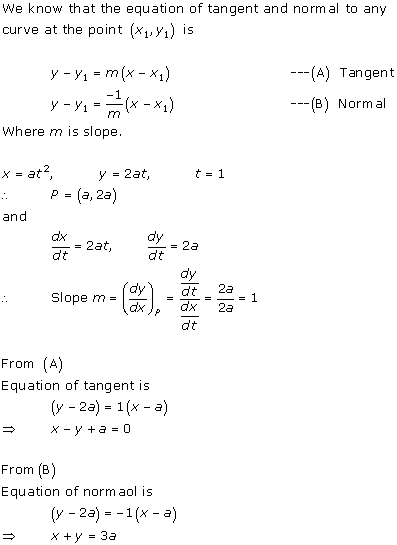
Solution 5(iv)
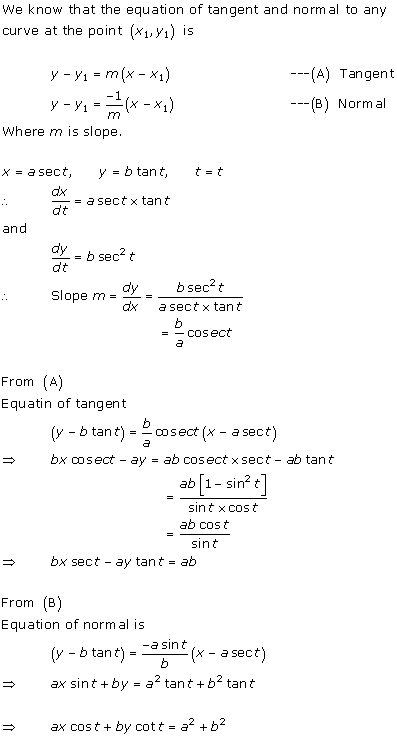
Solution 5(v)
Solution 5(vi)
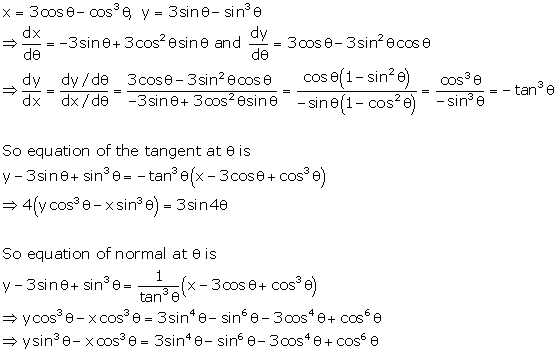
Solution 6
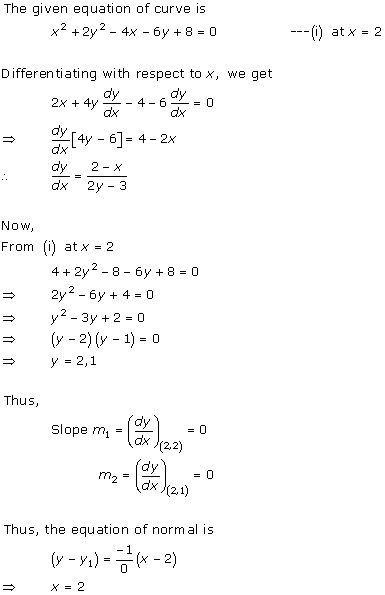
Solution 7
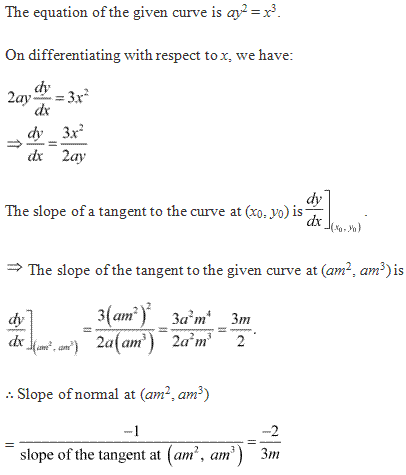
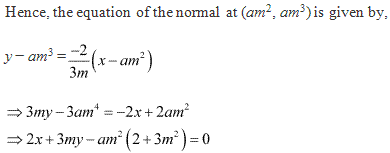
Solution 8
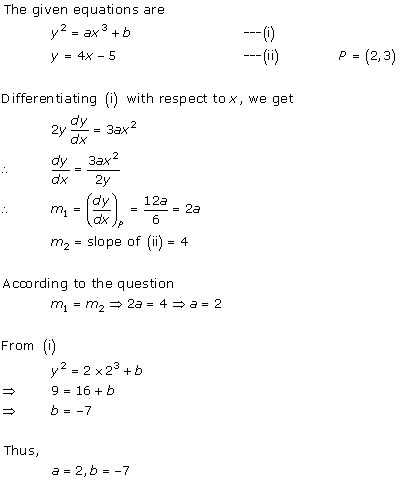
Solution 9
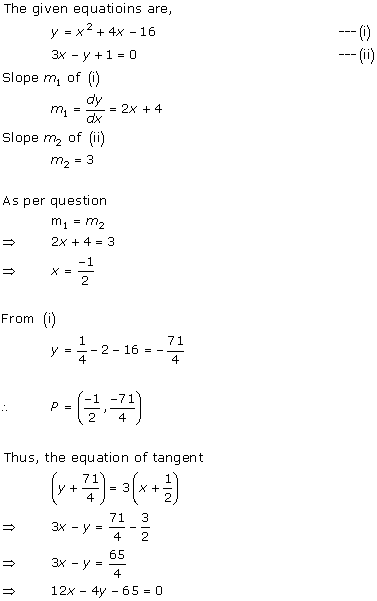
Solution 10
Solution 11
Solution 12
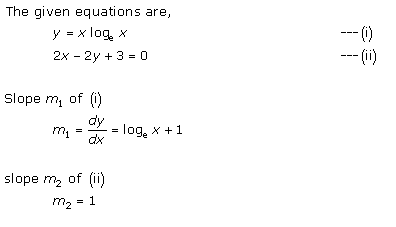
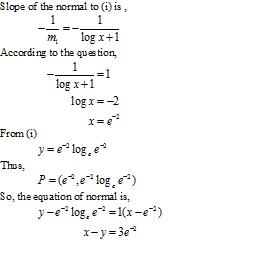
Solution 13
Solution 14
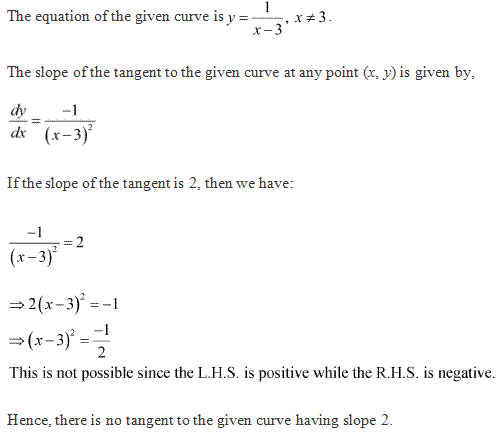
Solution 15
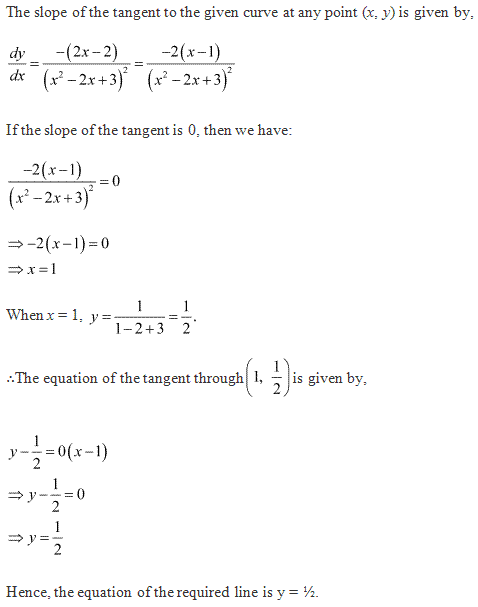
Solution 16
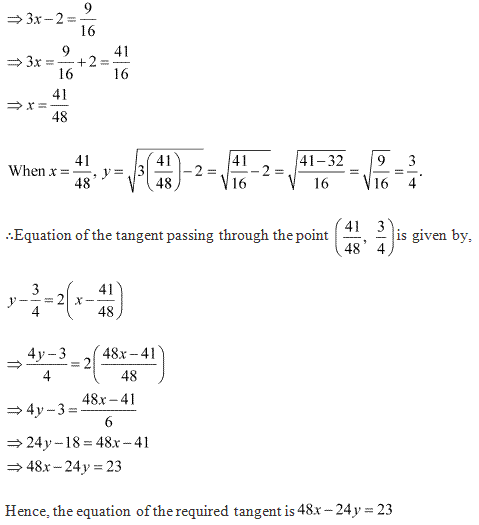
Solution 17
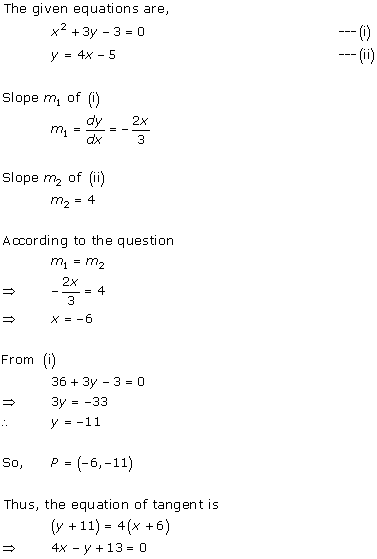
Solution 18
Solution 19
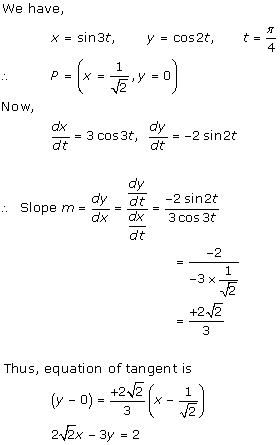
Solution 21
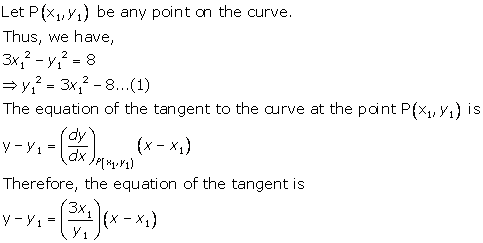
Solution 3(xvii)
Given equation
curve is 
Differentiating w.r.t x, we get
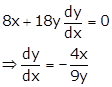
Slope of tangent
at 
is
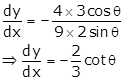
Slope of normal will be
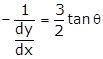
Equation of
tangent at will be
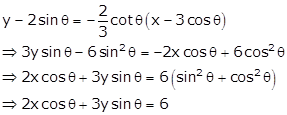
Equation of
normal at is
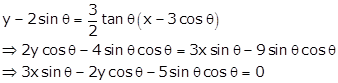
Solution 3(xviii)
Given equation
curve is 
Differentiating w.r.t x, we get
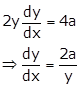
Slope of tangent
at 
is
Slope of normal will be
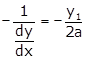
Equation of
tangent at will be
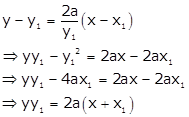
Equation of
normal at is
Solution 20
Given equation
curve is 
Differentiating w.r.t x, we get
As tangent is parallel to x-axis, its slope will be m = 0
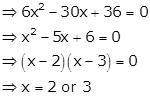
As this point lies on the curve, we can find y
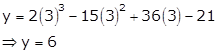
Or
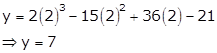
So, the points are (3, 6) and (2, 7).
Equation of tangent at (3, 6) is
y - 6 = 0 (x - 3)
y - 6 = 0
Equation of tangent at (2, 7) is
y - 7 = 0 (x - 2)
y - 7 = 0
Tangents and Normals Exercise Ex. 16.3
Solution 1(i)
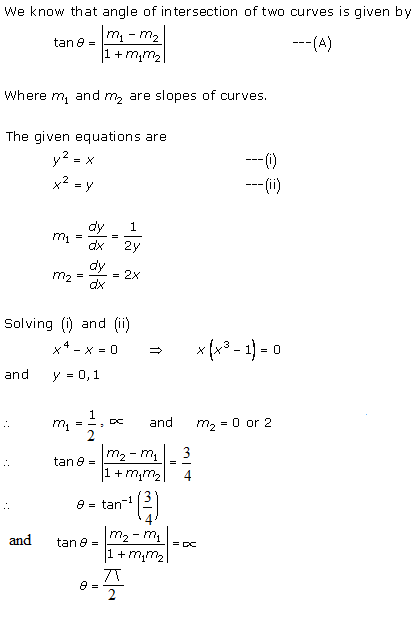
Solution 1(ii)
Solution 1(iii)
Solution 1(iv)
Solution 1(v)
Solution 1(vi)
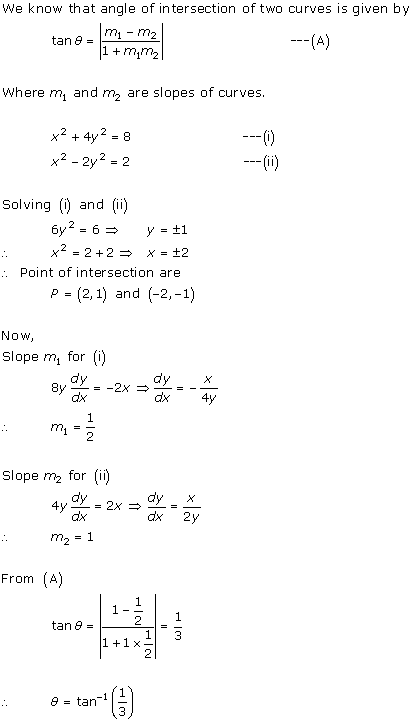
Solution 1(vii)
Solution 1(viii)
Solution 1 (ix)
Solution 2(i)
Solution 2(ii)
Solution 2(iii)
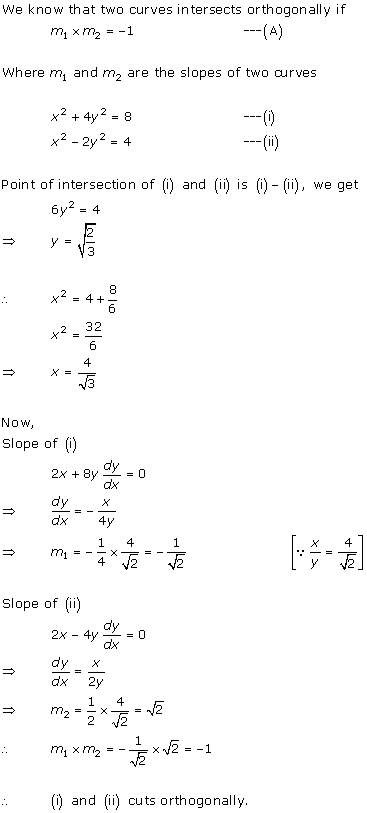
Solution 3(i)
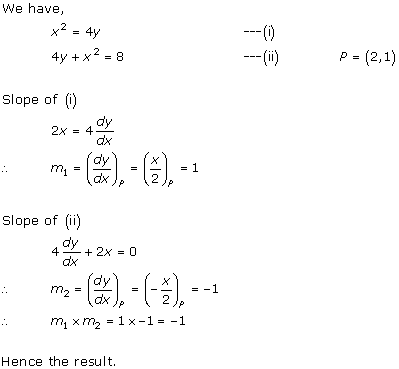
Solution 3(ii)
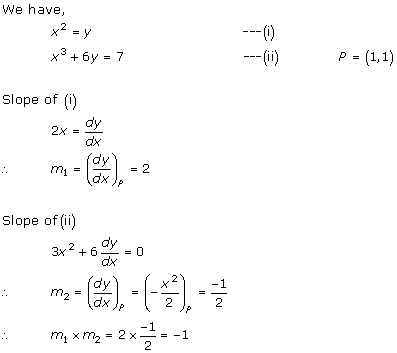
Solution 3(iii)
Solution 4
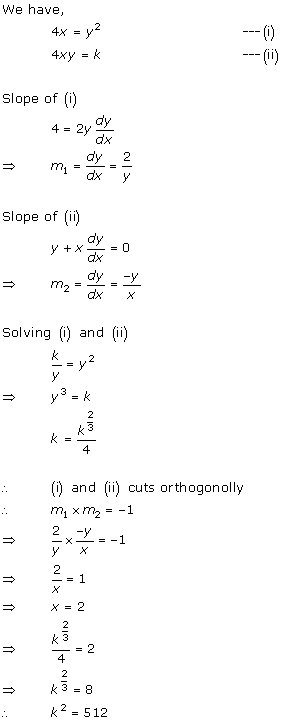
Solution 5
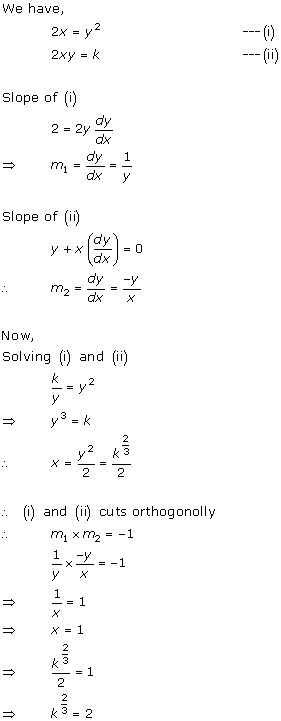
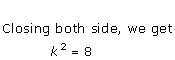
Solution 6
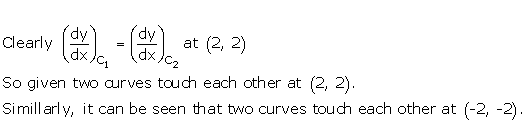
Solution 7
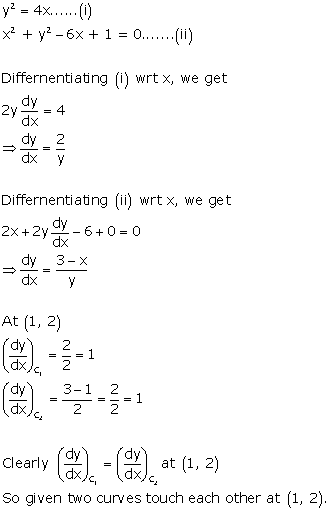
Solution 8(i)
Solution 8(ii)
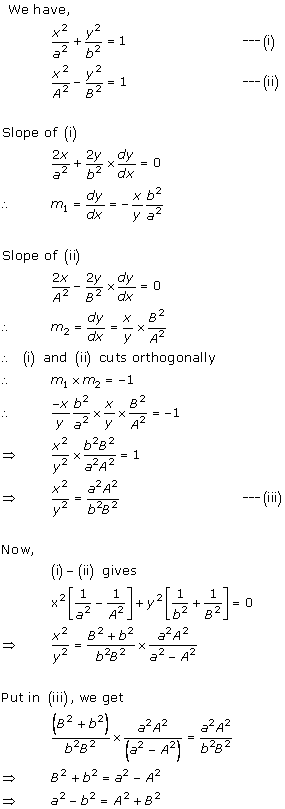
Solution 9
Solution 10
Tangents and Normals Exercise Ex. 16VSAQ
Solution 1
Solution 2
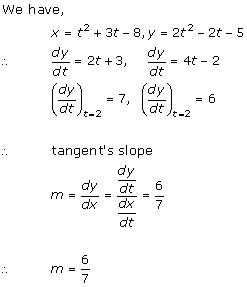
Solution 3
Solution 4
Solution 5
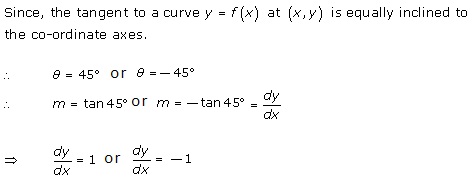
Solution 6
Solution 7
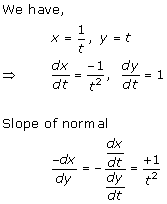
Solution 8
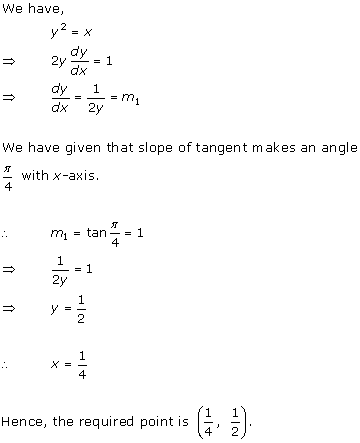
Solution 9
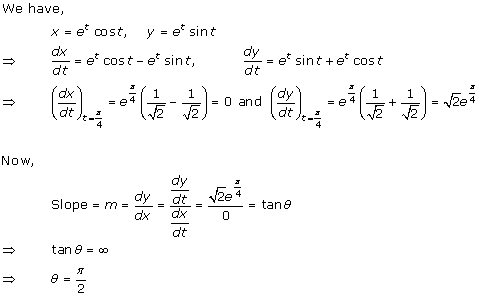
Solution 10
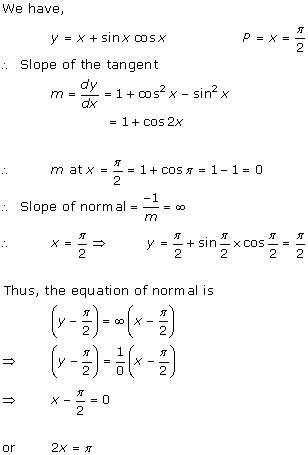
Solution 11
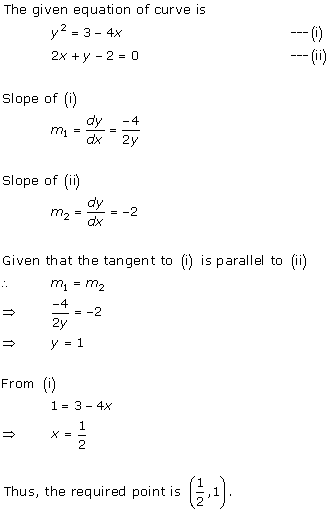
Solution 12
Solution 13
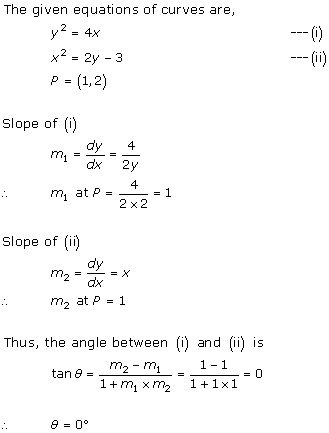
Solution 14
Solution 15
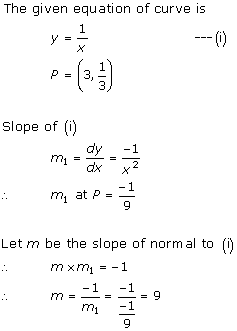
Solution 16
Solution 17
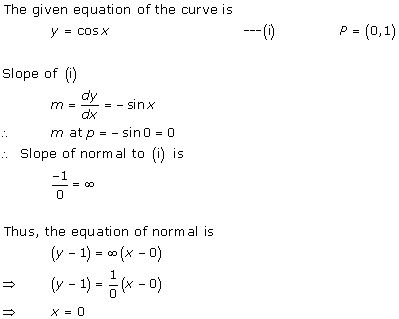
Solution 18
Given curve is y = sin x
Slope of tangent at (0, 0) is
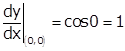
So, the equation of tangent at (0, 0) is
y - 0 = 1 (x - 0)
y = x
Solution 19
Given curve is 
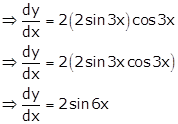
Slope of tangent at (0, 0) is
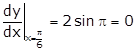
Hence, slope of
tangent at 
is 0.
