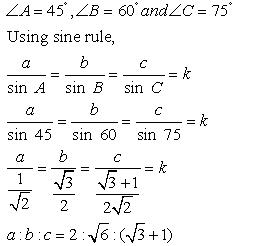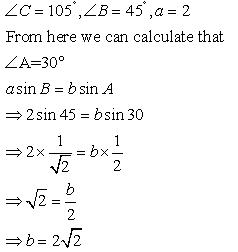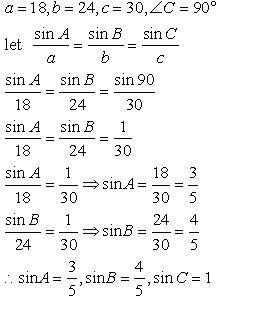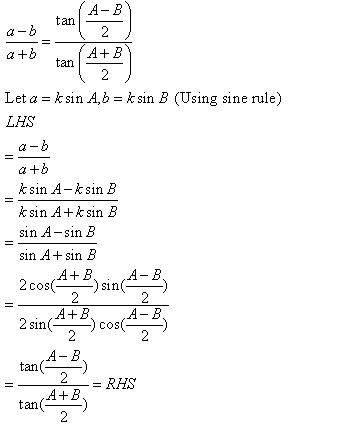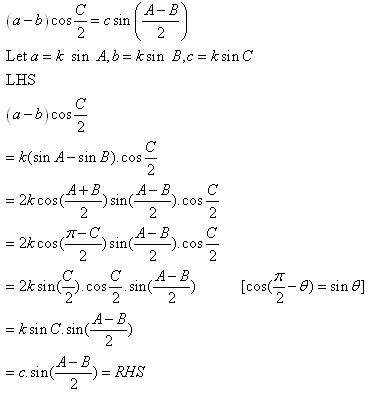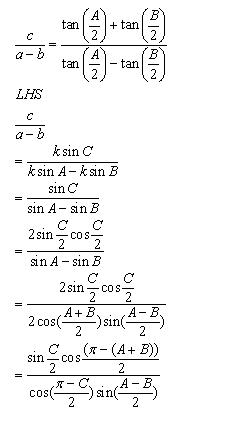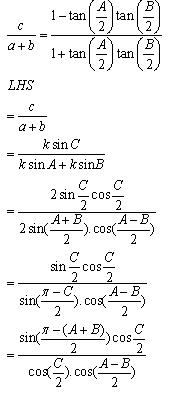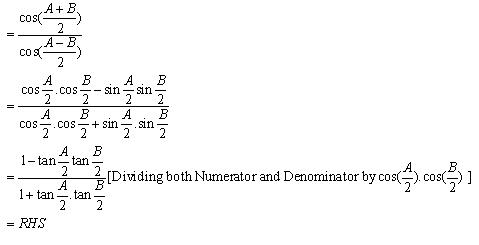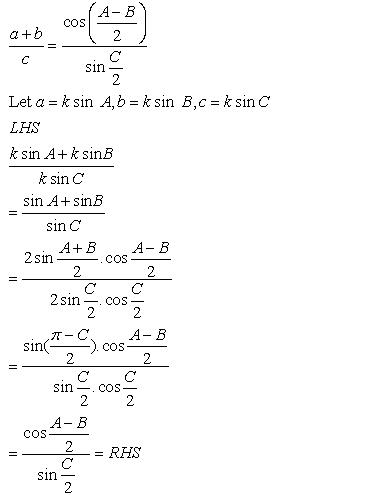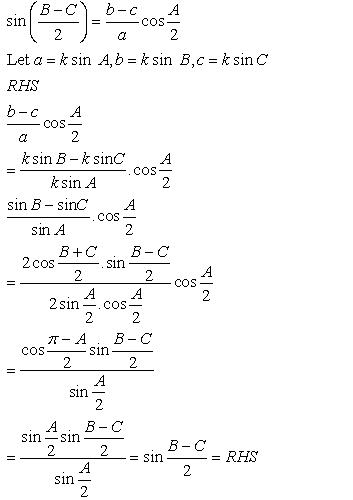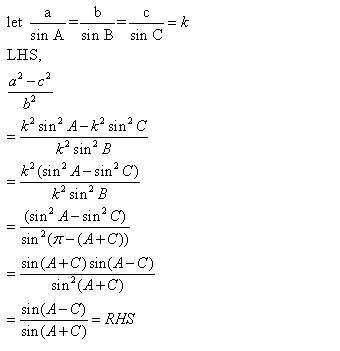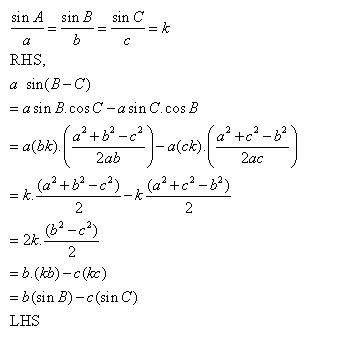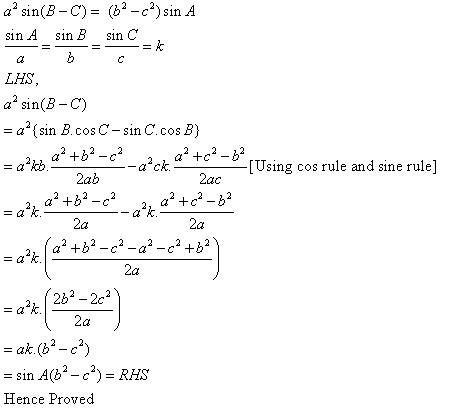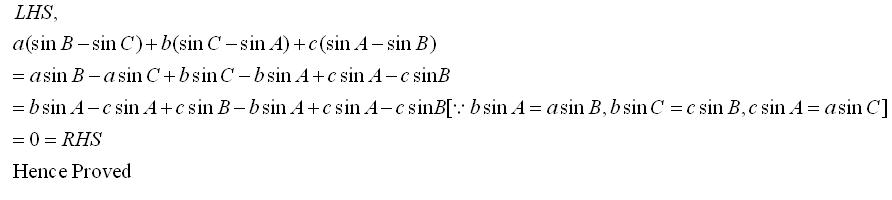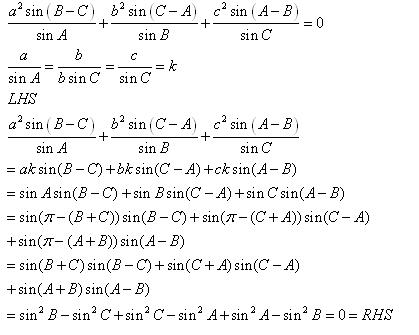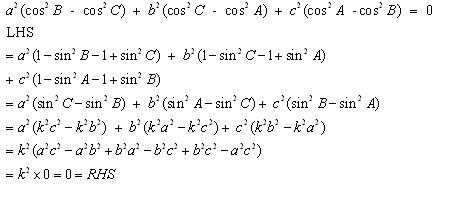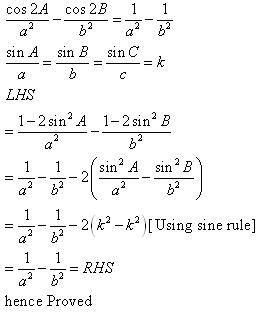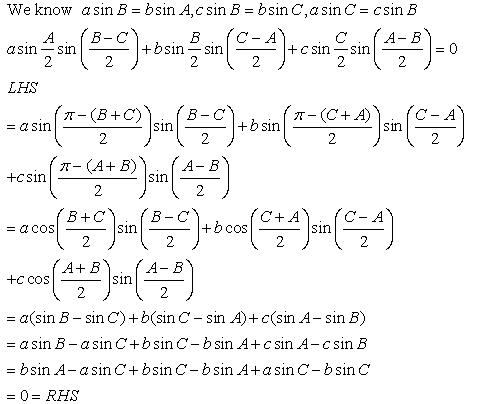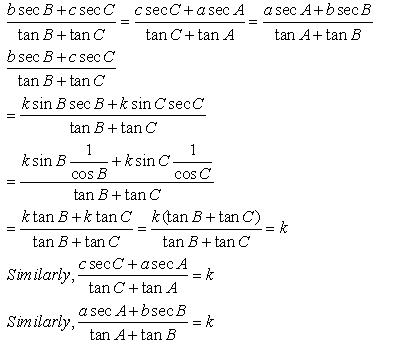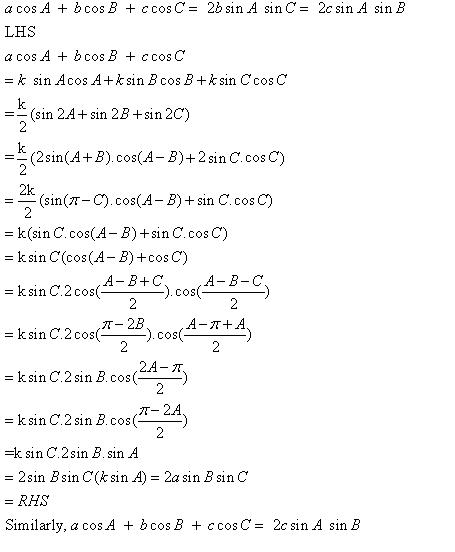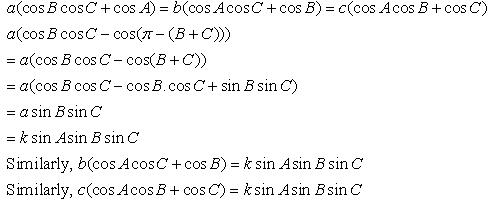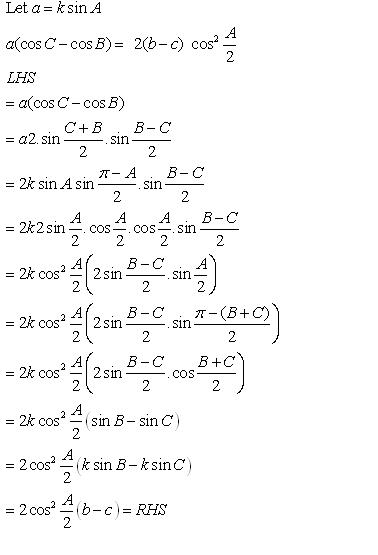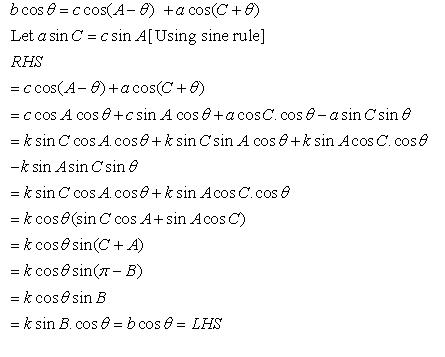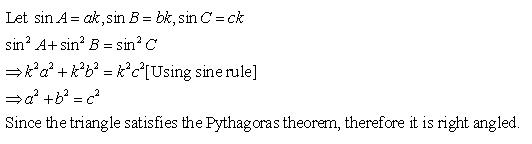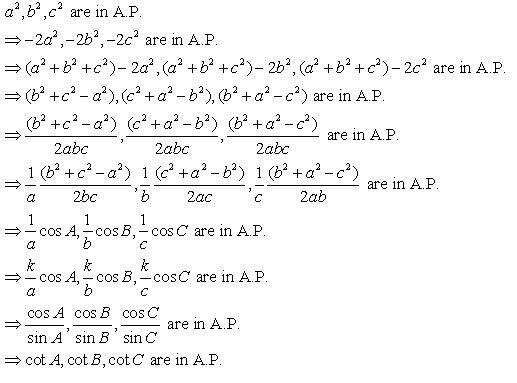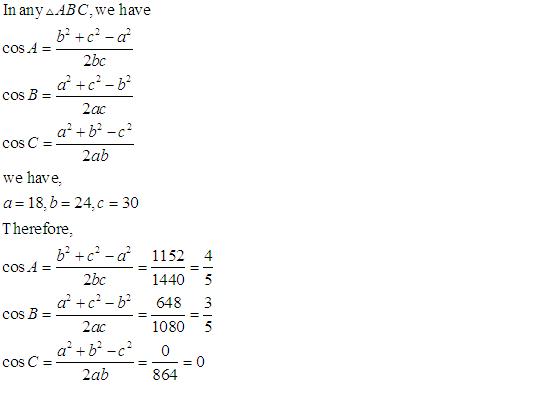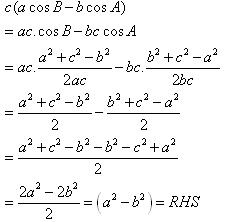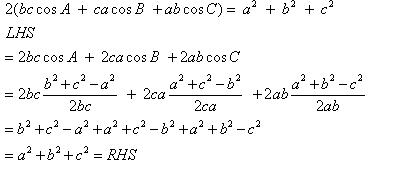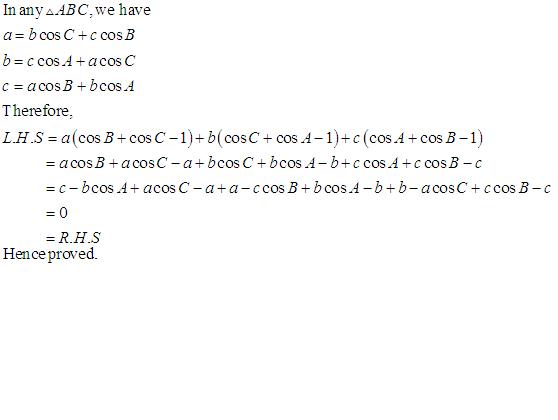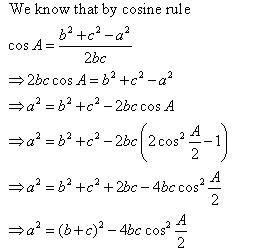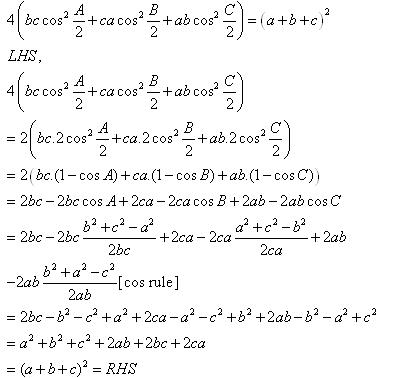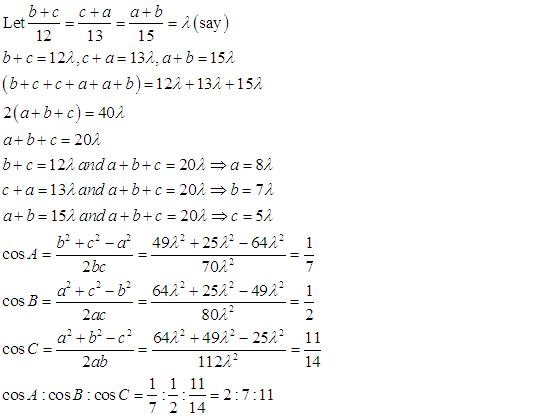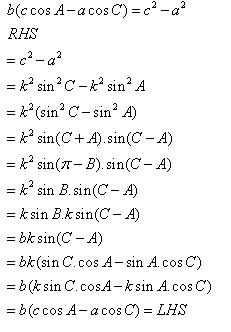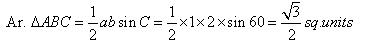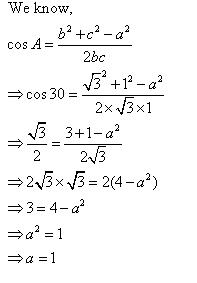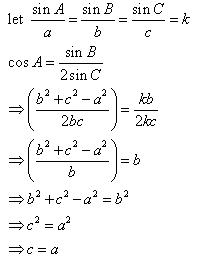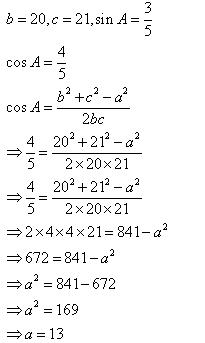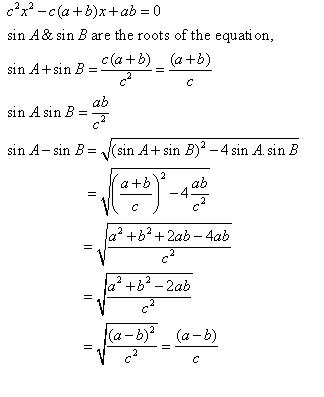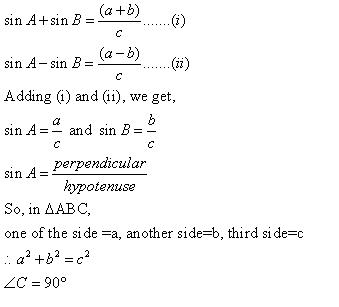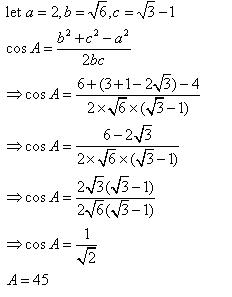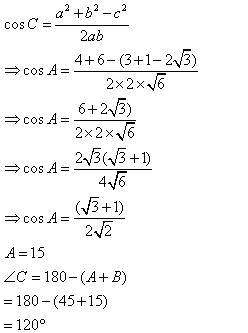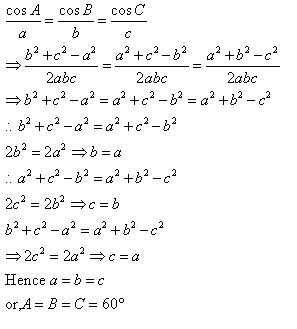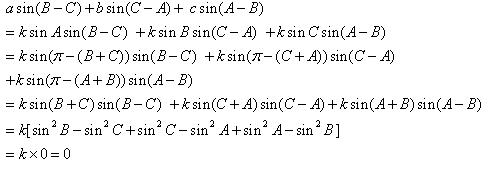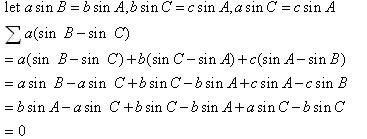Class 11-science RD SHARMA Solutions Maths Chapter 10 - Sine and Cosine Formulae and Their Applications
Ex. 10.1
Ex. 10.2
Ex. 10VSAQ
Sine and Cosine Formulae and Their Applications Exercise Ex. 10.1
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
Solution 24
Solution 25
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
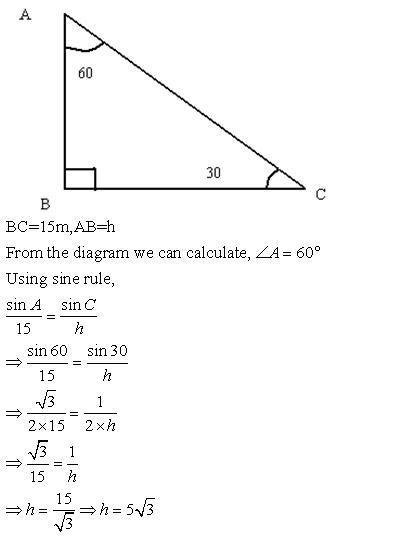
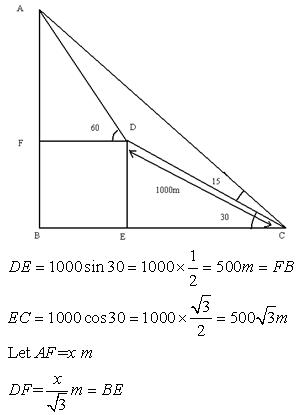
![]() .
.
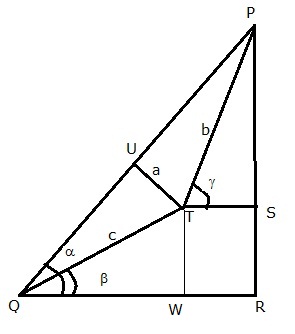

Solution 31
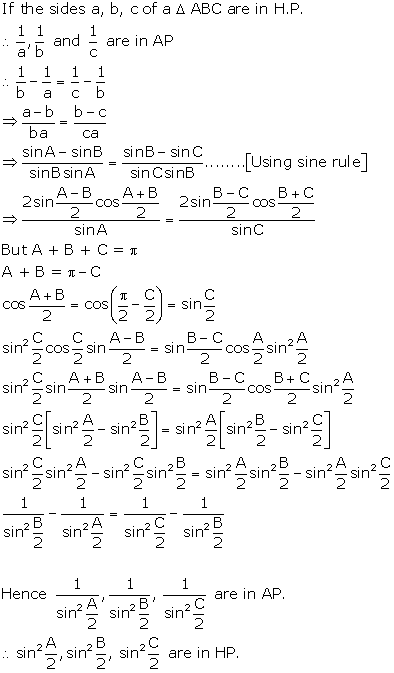
Sine and Cosine Formulae and Their Applications Exercise Ex. 10.2
Solution 1
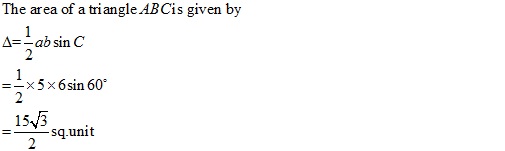
Solution 2

Solution 3
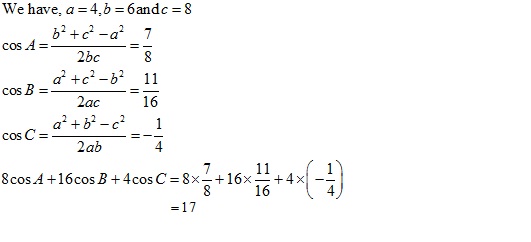
Solution 4
Solution 6
Solution 7
Solution 8
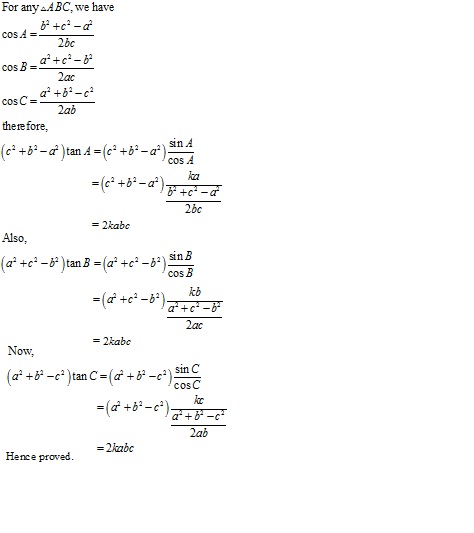
Solution 9
Solution 10
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
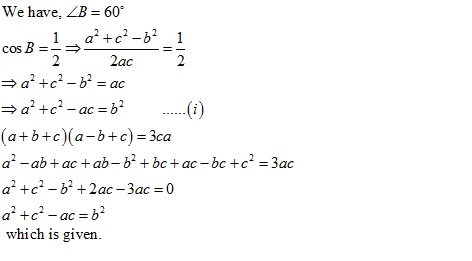
Solution 17

Solution 18
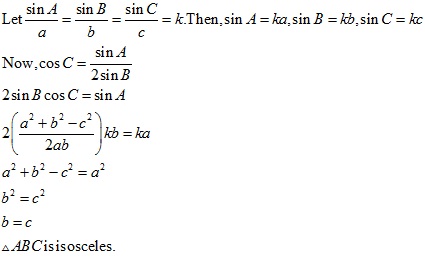
Solution 19
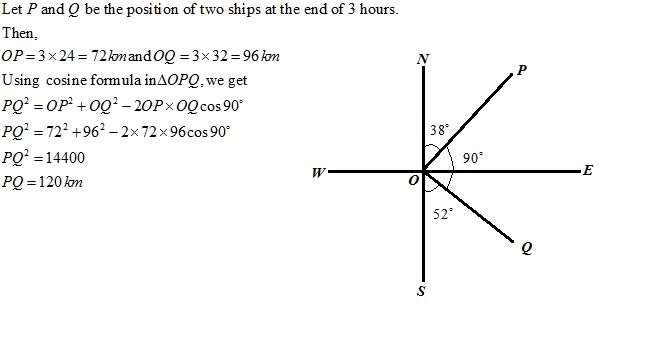
Solution 5
Solution 11
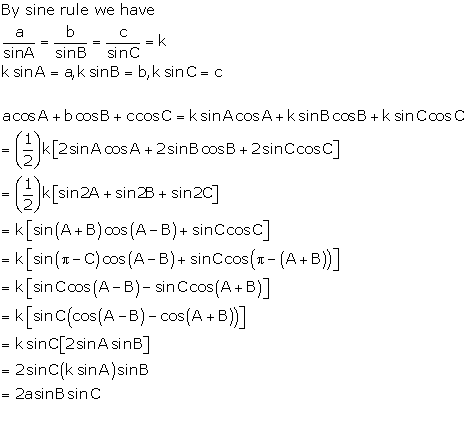
Sine and Cosine Formulae and Their Applications Exercise Ex. 10VSAQ
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
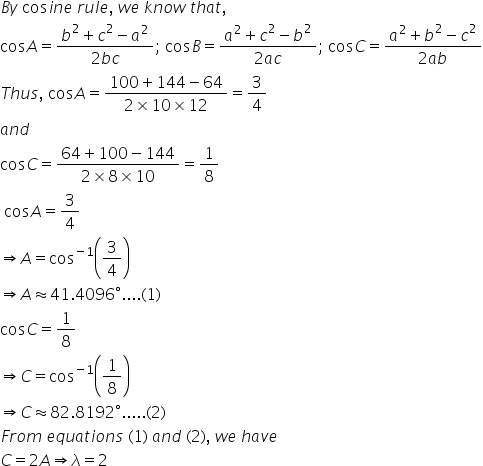
Solution 7
Solution 8
Solution 9