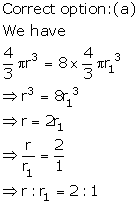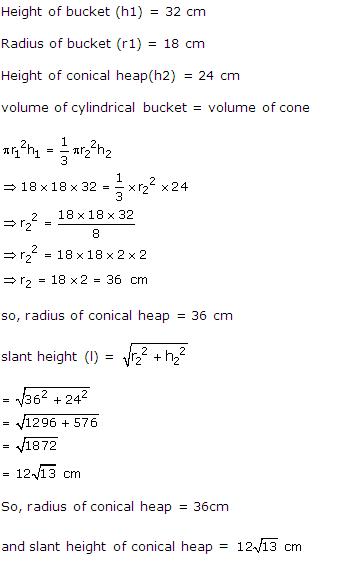Class 10 RD SHARMA Solutions Maths Chapter 14 - Surface Areas and Volumes
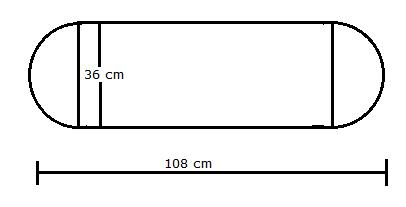
Surface Areas and Volumes Exercise Ex. 14.1
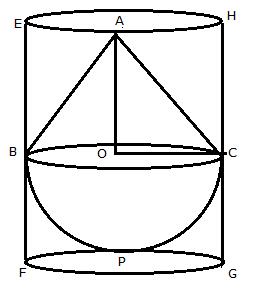
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6
Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12
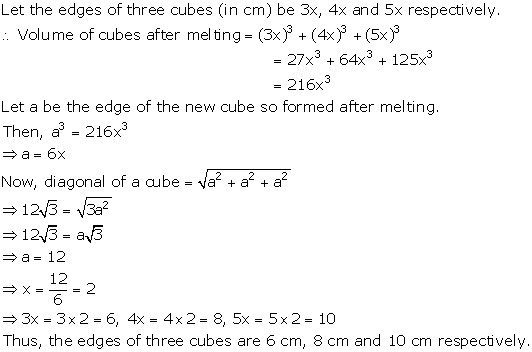
Solution 13

Solution 14

Solution 15
Solution 16

Solution 17
Solution 18

Solution 19
Solution 20
Solution 21
Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27
Solution 28

Solution 29

Solution 30

Solution 31
Solution 32
Solution 33

Solution 34

Solution 35
Solution 36

Solution 37

Solution 38

Solution 39

Solution 40

Solution 41

Solution 42

Solution 43
Solution 44
Solution 45
Solution 46

*Answer given in the book is incorrect.
Solution 47

Solution 48

Solution 49

Solution 50
Solution 51
Solution 52

Solution 53

Solution 54

Solution 55

Solution 56

Solution 57

Solution 58

Solution 59

Solution 60

Solution 61
Solution 62
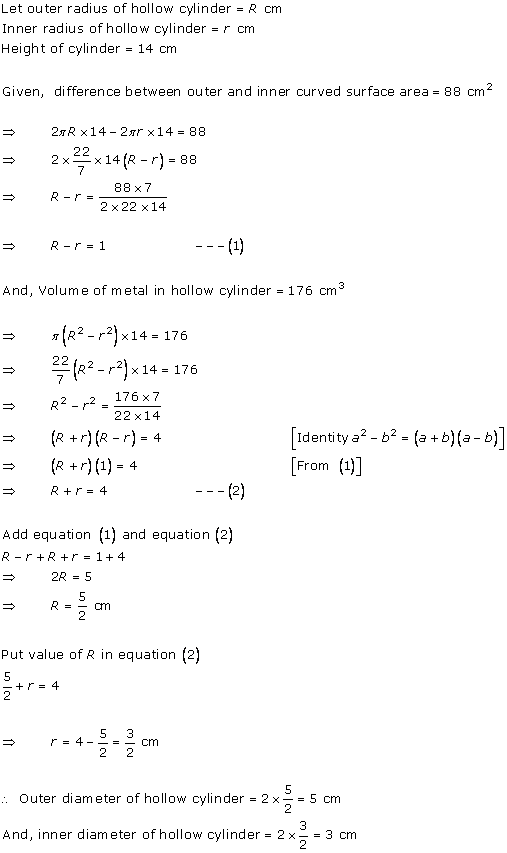
Solution 63

Solution 64
Solution 65

*Answer given in the book is incorrect.
Solution 66

Solution 67

Solution 68
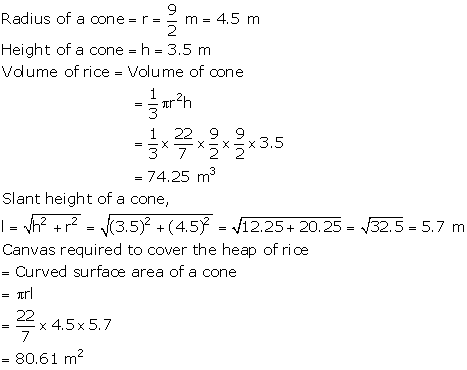
Solution 69

Solution 70

Solution 71

Solution 72
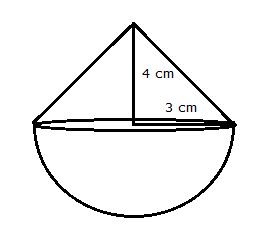
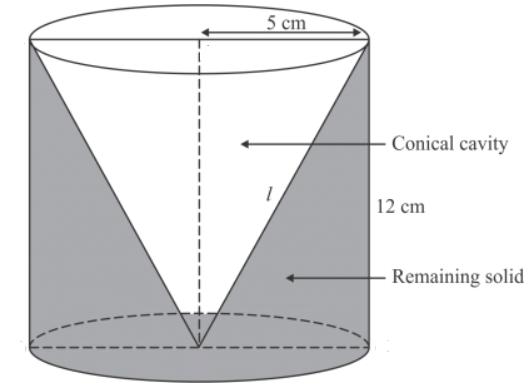
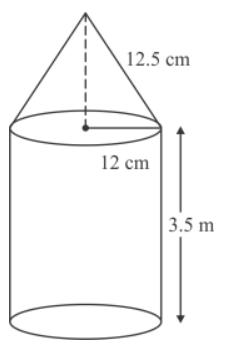
Height of the conical vessel h = 24 cm
Radius of the conical vessel r =5 cm
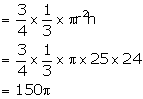
Let h be the height of the cylindrical vessel which is filled by water of the conical vessel.
Radius of the cylindrical vessel =10 cm
Volume of the cylindrical vessel = volume of water
π(10)2h=150π
h = 150π¸ 100π
h = 1.5 cm
Thus, the height of the cylindrical vessel is 1.5 cm.
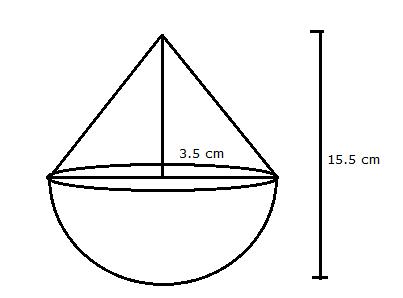
Surface Areas and Volumes Exercise Ex. 14.2
Solution 1
Solution 2
Solution 3

Solution 4

Solution 5

Solution 6
Solution 7

Solution 8
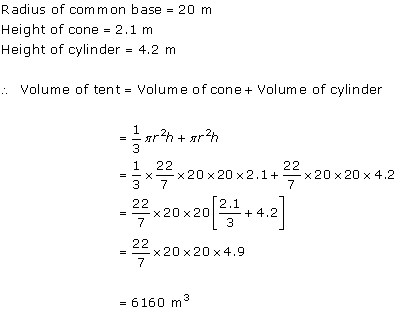
Solution 9
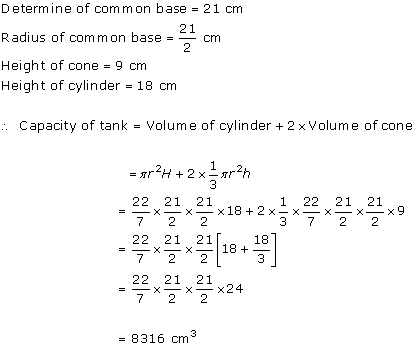
Solution 10

Solution 11

Solution 12

Solution 13
Solution 14

Solution 15
Solution 16
Solution 17

Solution 18

Solution 19

Solution 20

Solution 21
Solution 22
Solution 23

Solution 24
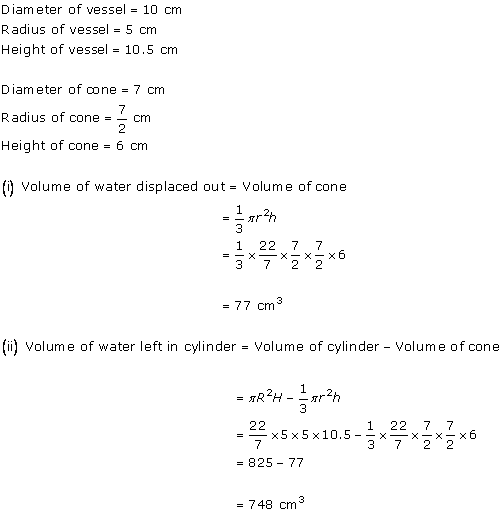
Solution 25

Solution 26
Solution 27
Solution 28

Solution 29

Solution 30

Solution 31

Solution 32
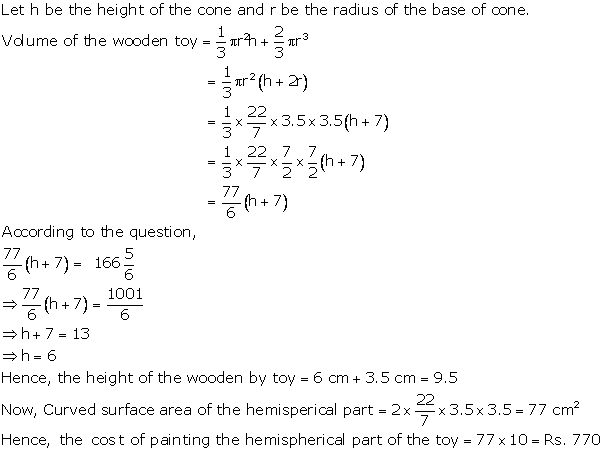
Solution 33

Solution 34
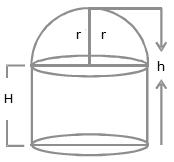

Solution 35
Solution 36
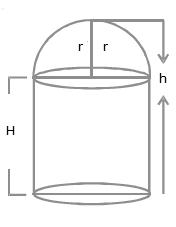

Solution 37


Solution 38
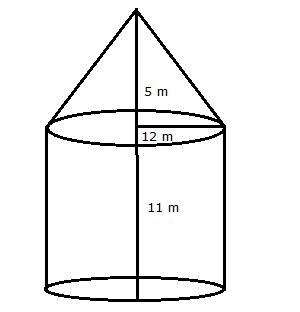
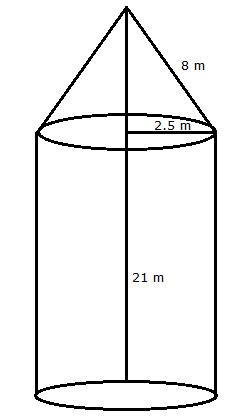
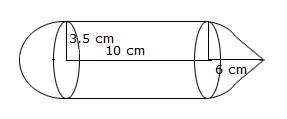
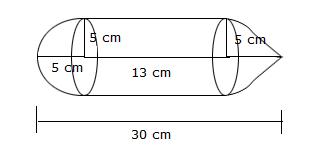
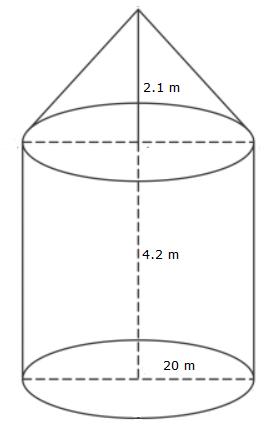
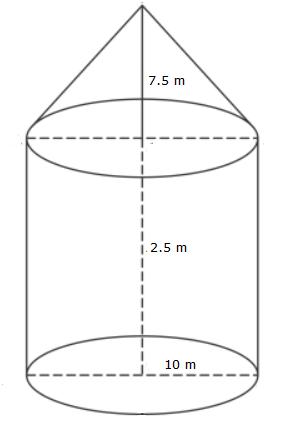
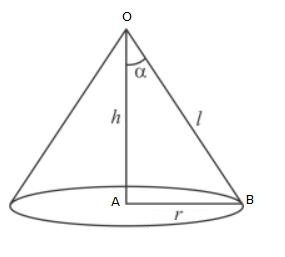
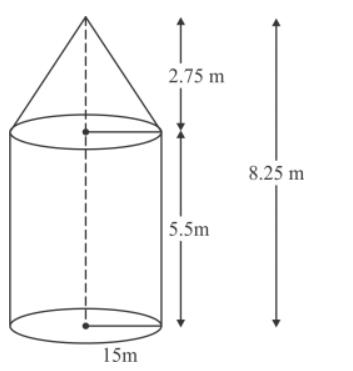
Total area of the canvas = curved surface area of the cone + curved surface area of a cylinder radius = 28 m height (cylinder) = 6 m
height (cone) = 21 m
l = slant height of cone
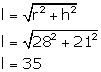
curved surface area of the cone = πrl
=π×28×35
=![]() ×28×35 = 3080 m2
×28×35 = 3080 m2
curved surface area of the cylinder = 2πrh
=2×![]() ×28×6
×28×6
=1056
Total area of the canvas = 3080+1056 =4136 m2
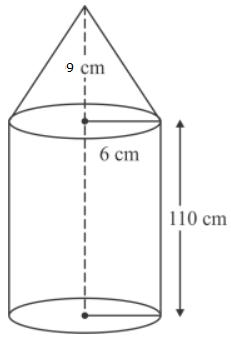
Surface Areas and Volumes Exercise Ex. 14.3
Solution 1
Solution 2
Solution 3

Solution 4

Solution 5

Solution 6
Solution 7

Solution 8

Solution 9

Solution 10
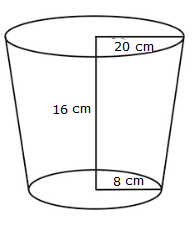

Solution 11
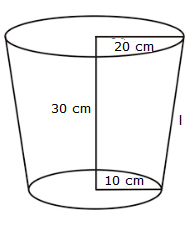

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18
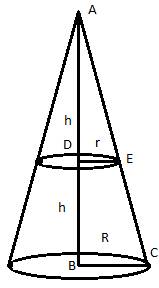

Solution 19

Solution 20
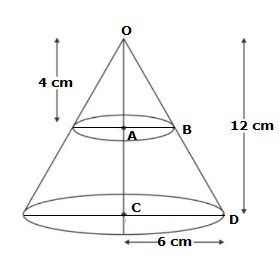

Solution 21
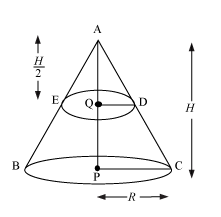
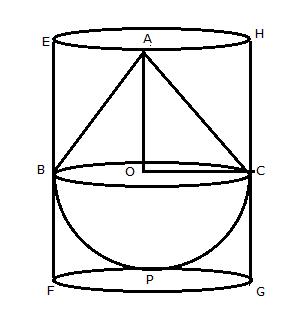
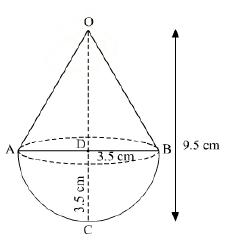
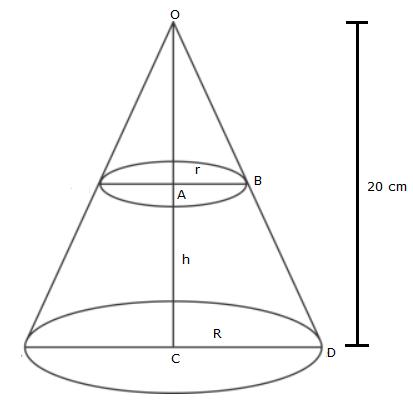
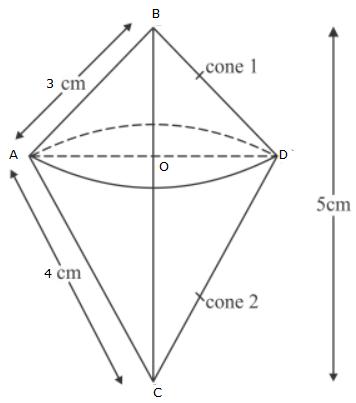
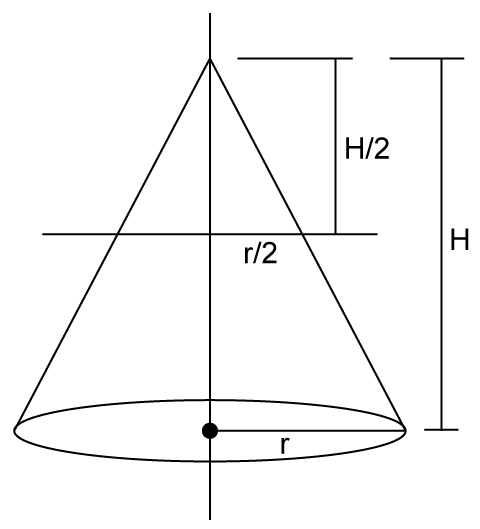
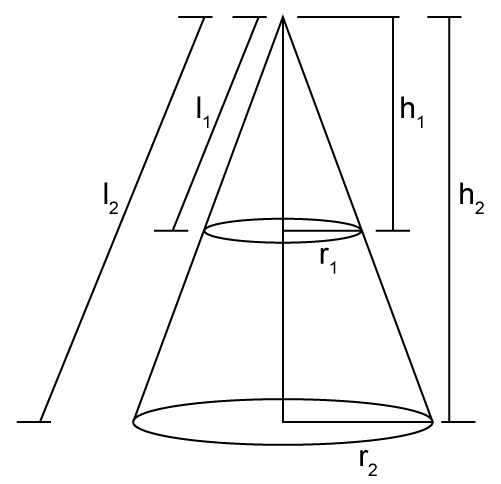
Let the height of the cone be H and the radius be R. This cone is divided into two equal parts.
AQ=1/2 AP
Also,
QP||PC
Therefore,ΔAQD~ΔAPC.
So,

Solution 22
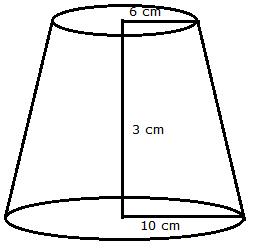
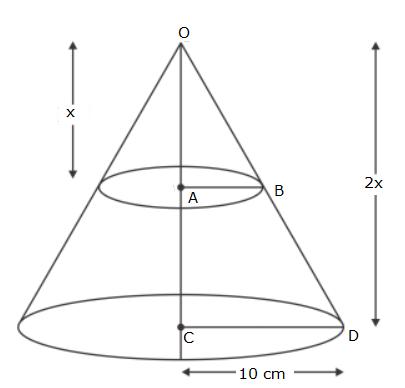
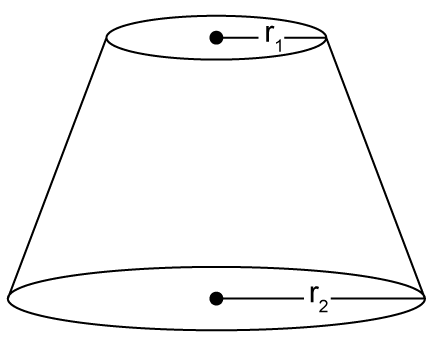
A bucket, made of metal sheet, is in the form of a cone.
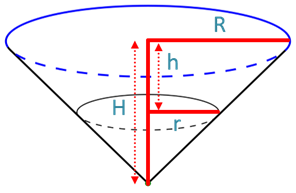
R = 15 cm, r = 6 cm and H=35 cm
Now, using the similarity concept, we can writ
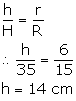
Volume of the frustum is
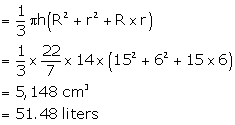
The rate of milk is Rs. 40 per litre.
So, the cost of 51.48 litres is Rs. 2059.20.
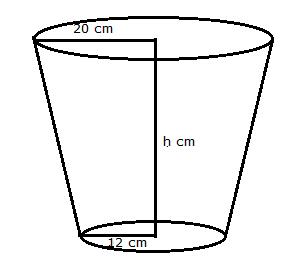
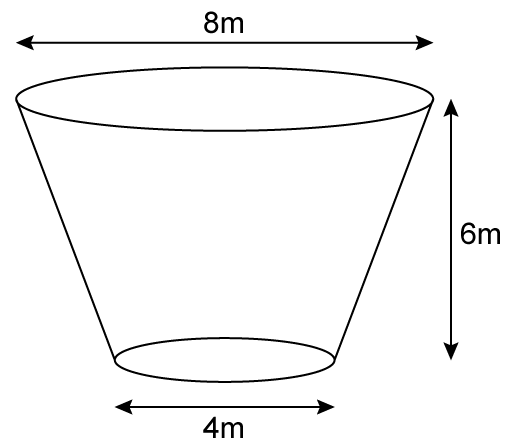
Solution 23
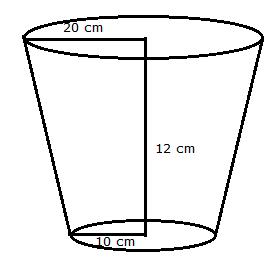
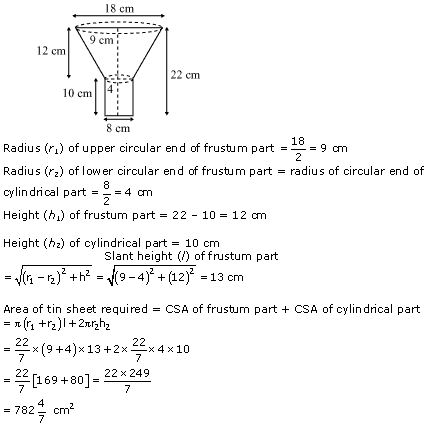
(i)
Given:
Radius of lower end (r1) = Diameter/2 = 5 cm
Radius of upper end (r2) = Diameter/2 = 15 cm
Height of the bucket (h) = 24 cm
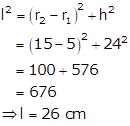
Area of metal sheet used in making the bucket
= CSA of bucket + Area of smaller circular base
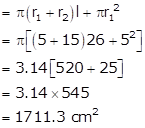
Hence, area of the metal sheet used in making the bucket is 1711.3 cm2.
(ii)
We should avoid the bucket made by ordinary plastic because it is less strength than metal bucket and also not ecofriendly.
Surface Areas and Volumes Exercise Rev. 14
Solution 1

Solution 2

Solution 3
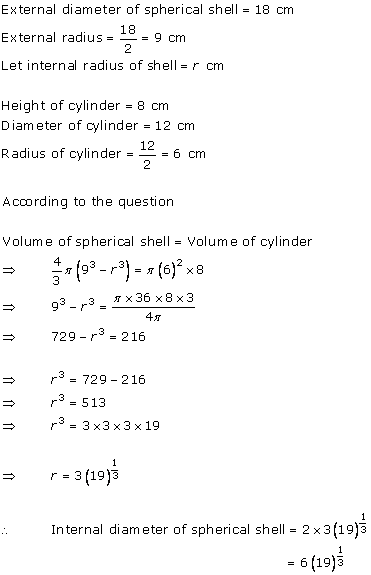
Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10
Solution 11

Solution 12

Solution 13
Solution 14

Solution 15

Solution 16

Solution 17
Solution 18

Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27

Solution 28

Solution 29

Solution 30

Solution 31
Solution 32

Solution 33
Solution 34
Solution 35

Solution 36

Solution 37

Solution 38

Solution 39

Solution 40

Solution 41

Solution 42
Solution 43

Solution 44

Solution 45

Solution 46
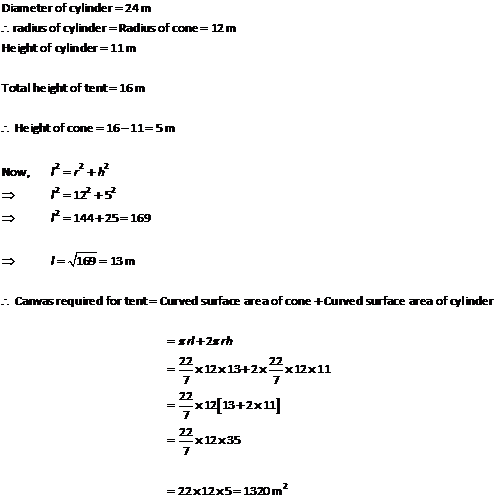
Solution 47

Solution 48

Solution 49

Solution 50

Solution 51
Solution 52

Solution 53

Solution 54

Solution 55
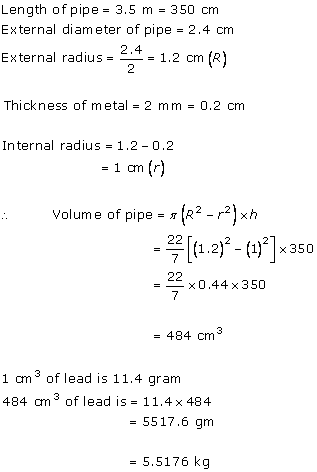
Solution 56

Solution 57

Solution 58

Solution 59

Solution 60

Solution 61
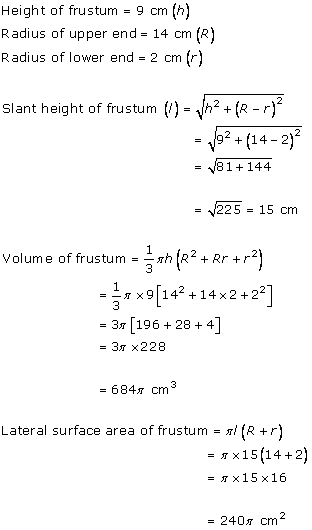
Solution 62

Solution 63

Solution 64

Solution 65
Solution 66

Solution 67

Solution 68

Solution 69

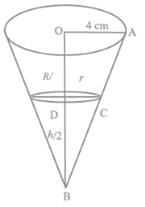

Solution 70

Solution 71

Solution 72
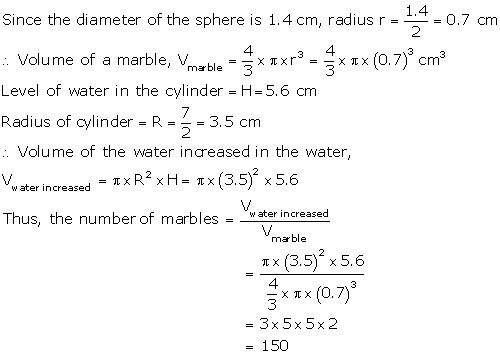
Solution 73
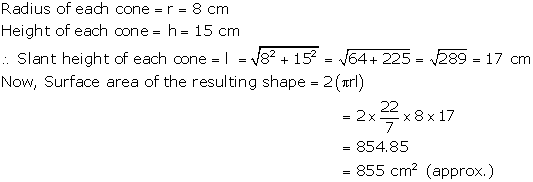
Solution 74

Solution 75
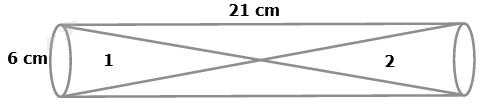
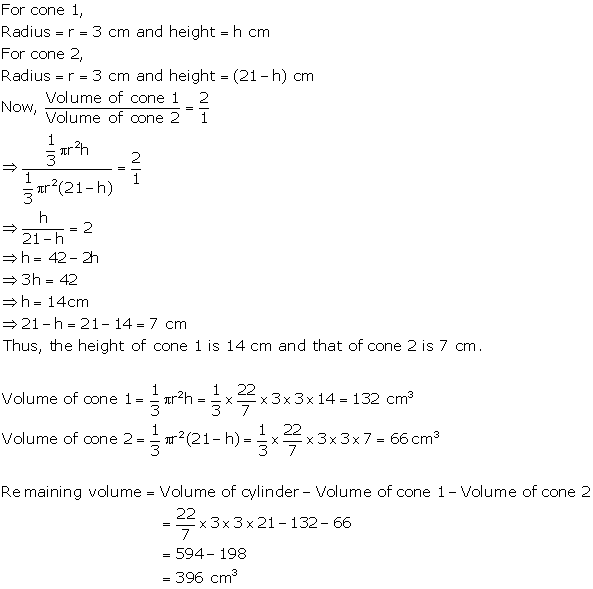
Solution 76

Surface Areas and Volumes Exercise 14.88
Solution 1
After melting a sphere and converting it into a wire, the volume remains same.

So the correct option is (c).
Solution 2
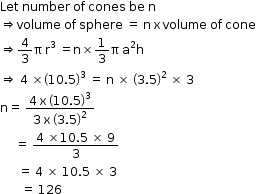
So, the correct option is (b).
Solution 3


So the correct option is (b).
Solution 4

Solution 5
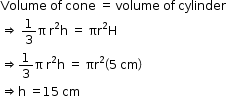
So, the correct option is (b).
Solution 6

So, the correct option is (d).
Solution 7

So, the correct option is (c).
Solution 8
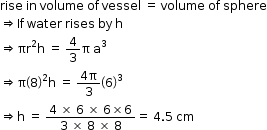
So, the correct option is (a).
Solution 9

So, correct option is (b).
Solution 10

So, the correct option (d).
Solution 11
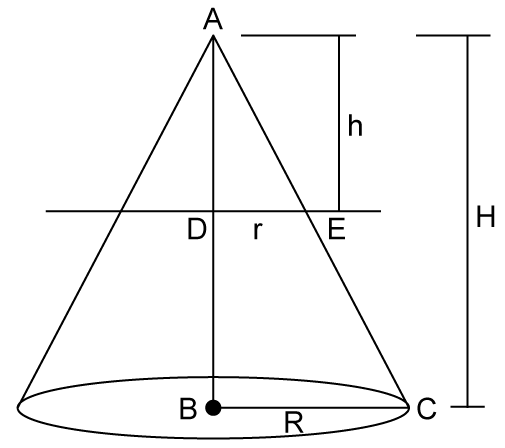

So, the correct option is (c).
Solution 12
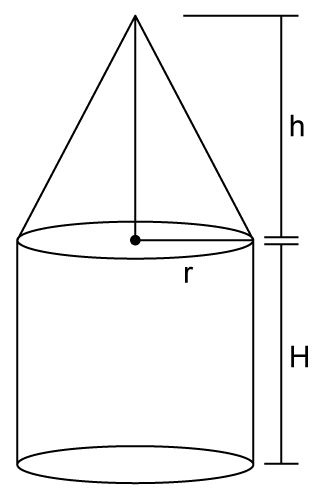
So, the correct option is (b).
Surface Areas and Volumes Exercise 14.89
Solution 13
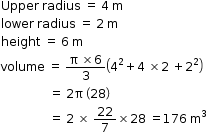
So, the correct option is (a).
Solution 14

So, the correct option is (b).
Solution 15
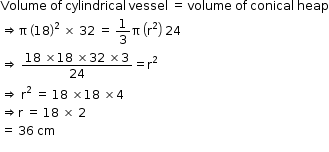
So, the correct option is (c).
Solution 16
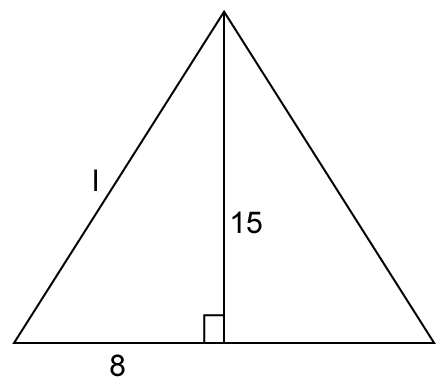

So, the correct option is (d).
Solution 17

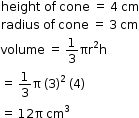
So, the correct option is (a).
Solution 18

So, the correct option is (b).
Solution 19
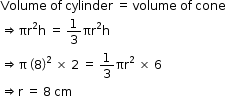
So, the correct option is (d).
Solution 20
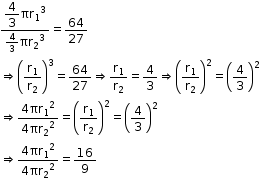
So, the correct option is (d).
Solution 21
Volume of the sphere = Sum of the volume of the three spheres
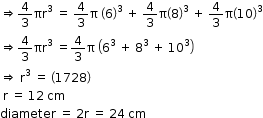
So, correct option is (b).
Solution 22

So, correct option is (c).
Solution 23
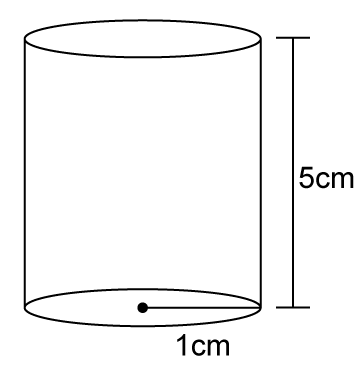

So, correct option is (a).
Solution 24

So, the correct option is (c).
Surface Areas and Volumes Exercise 14.90
Solution 25
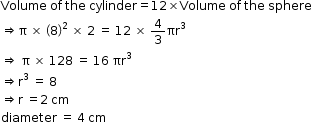
So, correct option is (d).
Solution 26
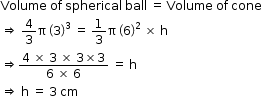
So, the correct option is (b).
Solution 27
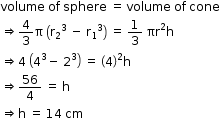
So, the correct option is (b).
Solution 28

So, the correct option is (a).
Solution 29
Diameter = 1.6 m = 160 cm
So, radius = 80 cm

So, the correct option is (b).
Solution 30
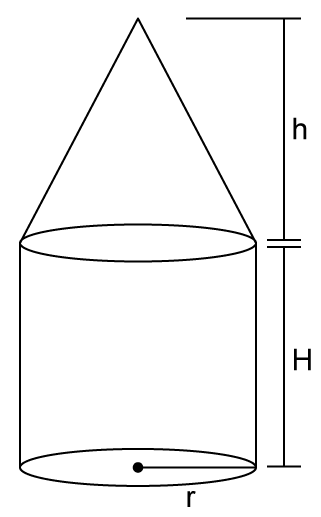
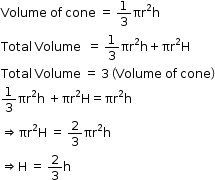
So, the correct option is (d).
Solution 31
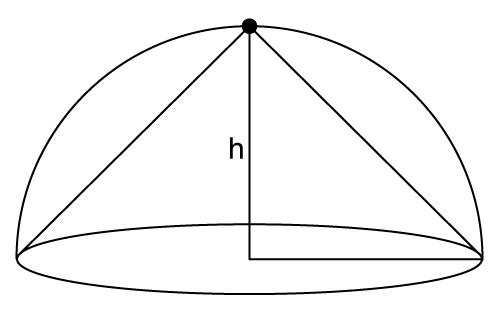
So, correct option is (b).
Solution 32

So, the correct option is (a).
Solution 33
The cylinder completely encloses the sphere.
Hence, diameter of the sphere = diameter of the cylinder = 2r
Now, h is also given to be 2r.
So, the correct option is (a) or (c).
Note: Both can be the answer since h = 2r.
Solution 34

So, the correct option is (a).
Solution 35
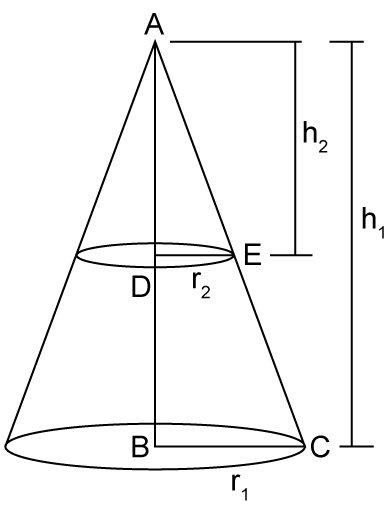
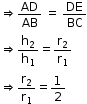
So, the correct option is (b).
Solution 36
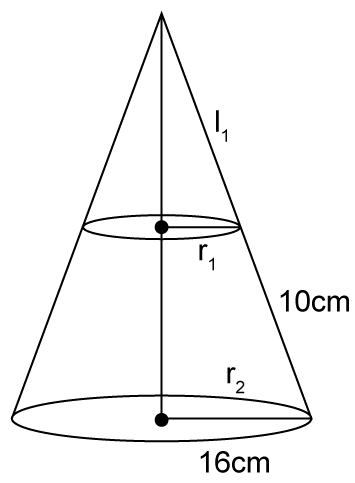

So, the correct option is (c).
Solution 37
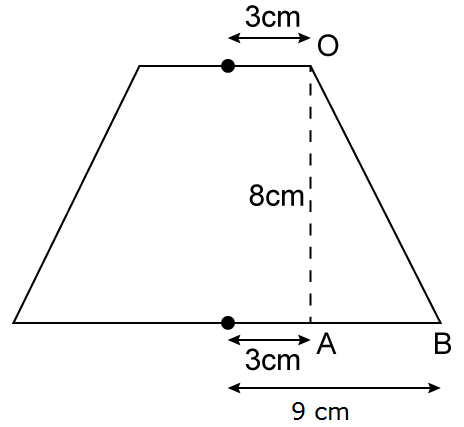
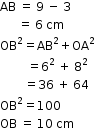
So, the correct option is (c).
Surface Areas and Volumes Exercise 14.91
Solution 38

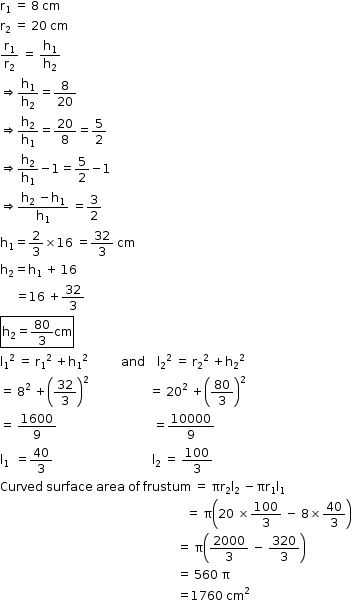
So, the correct option is (a).
Solution 39

So, the correct option is (c)
Solution 40

So, the correct option is (b).
Solution 41

So, the correct option is (c).
Solution 42
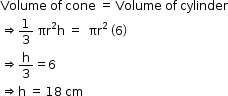
So, the correct option is (c).
Solution 43

So, the correct option is (a).
Solution 44

So, the correct option is (b).
Solution 45
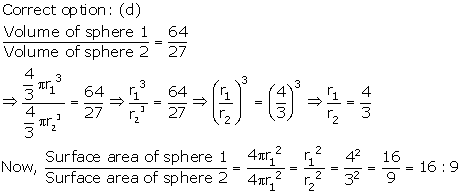
Solution 46
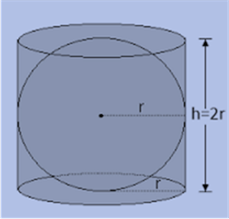
Correct option: (b)
From the figure, it is clear that diameter of sphere is 2r.
Solution 47

Correct option: (a)
In a right circular cone, the cross-section made by a plane parallel to the base is a circle.
Solution 48
Correct option: (a)
When two solid-hemispheres of same base radius r are joined together along their bases, it forms a sphere.
And, CSA of sphere = 4πr2
Solution 49

Solution 50