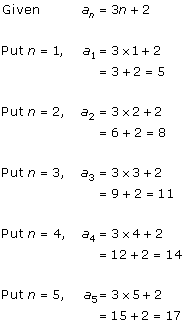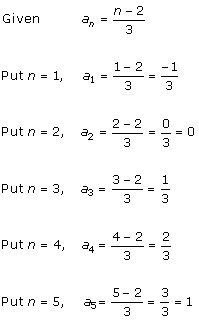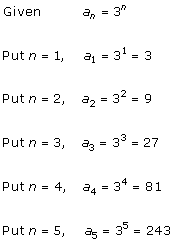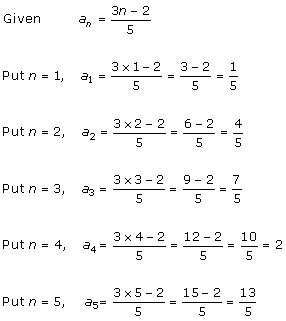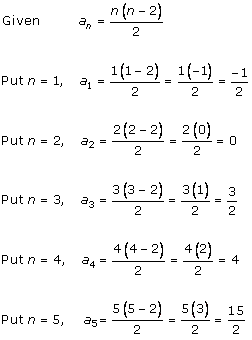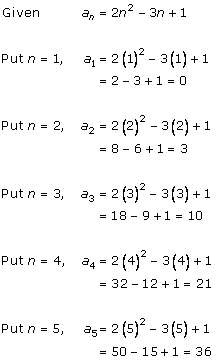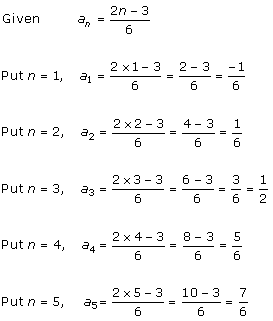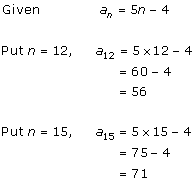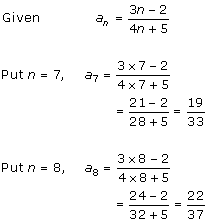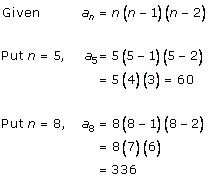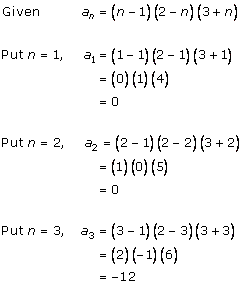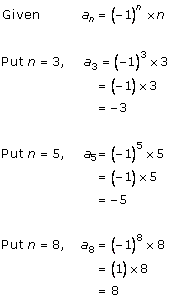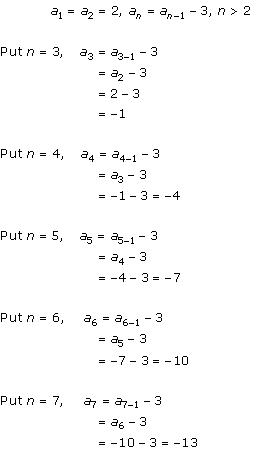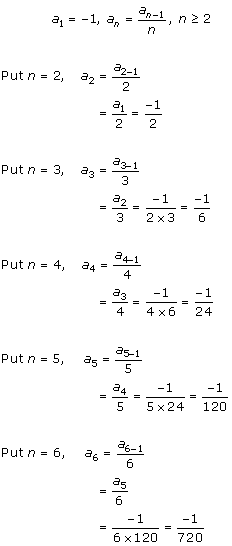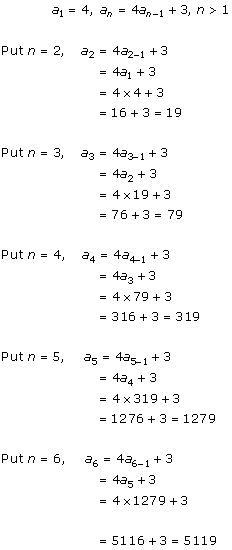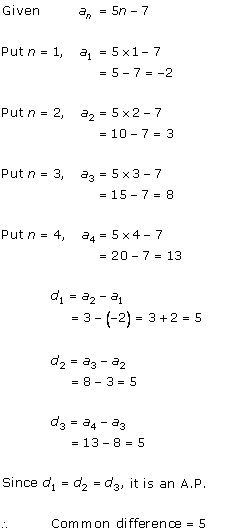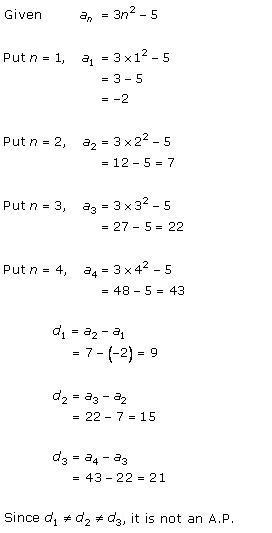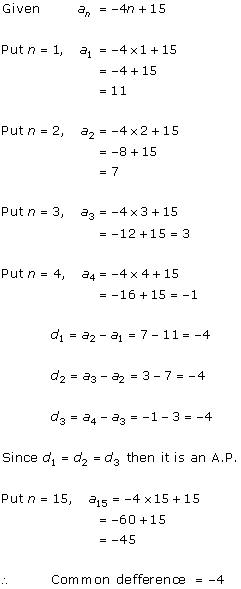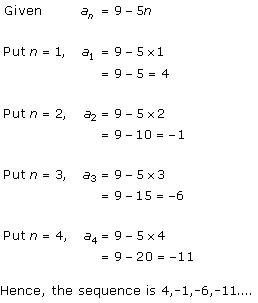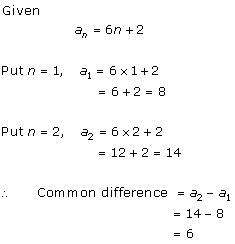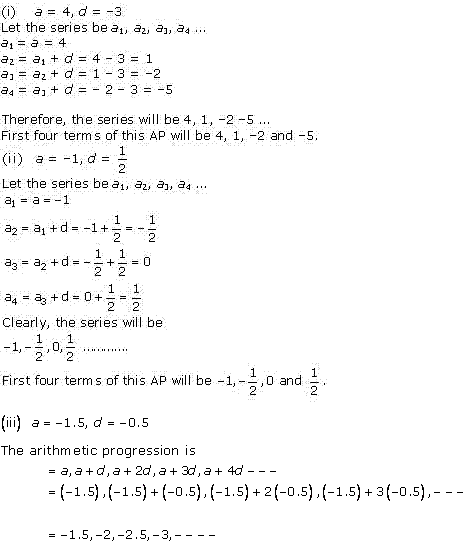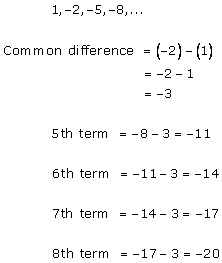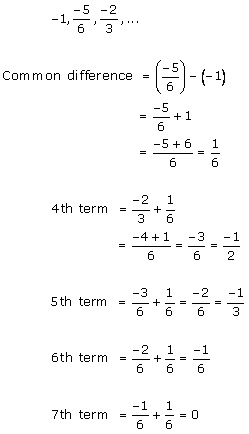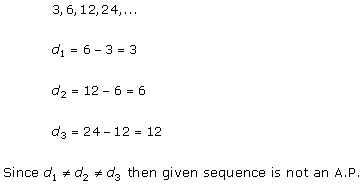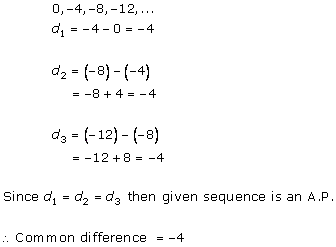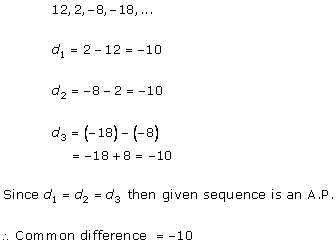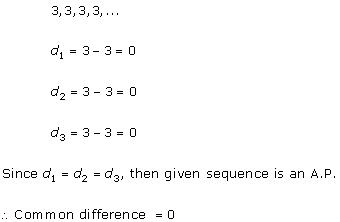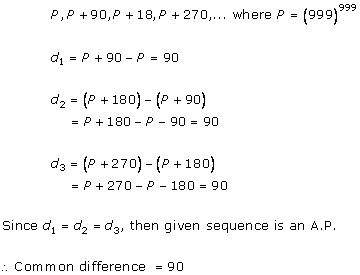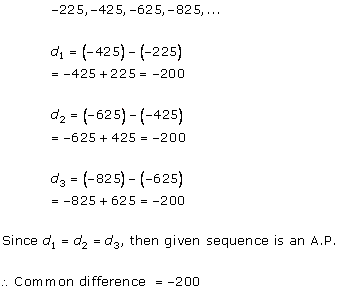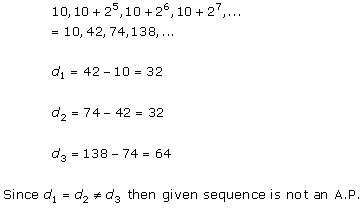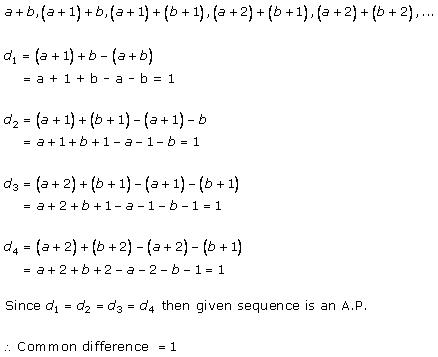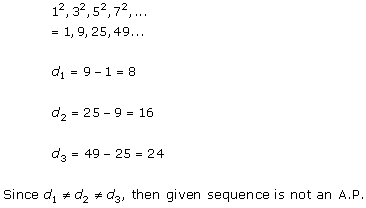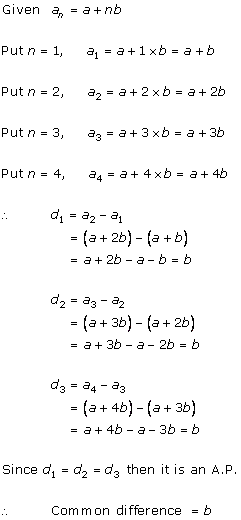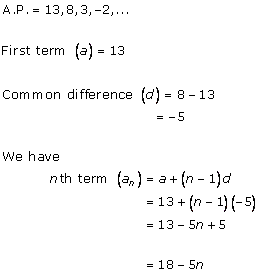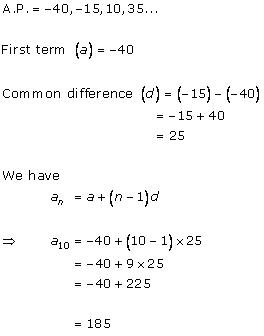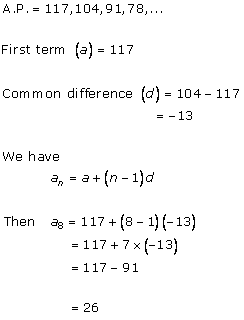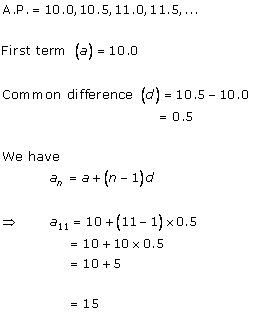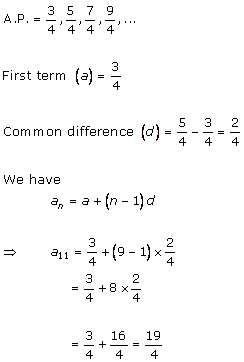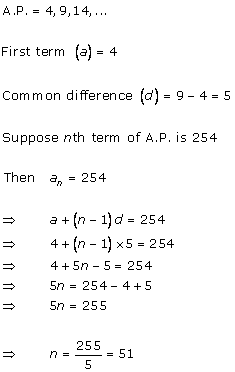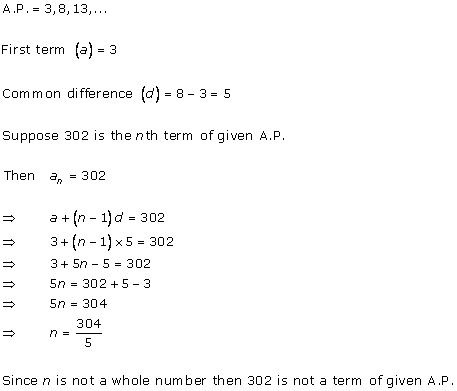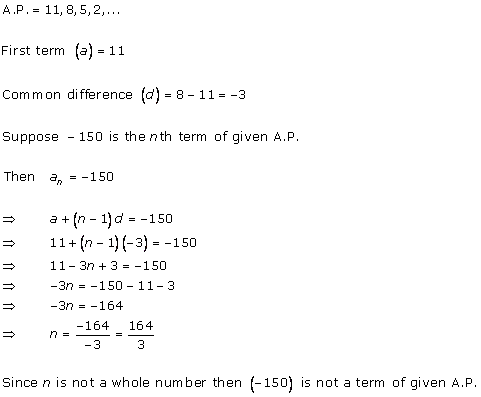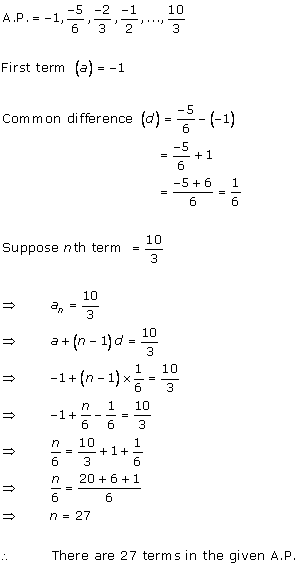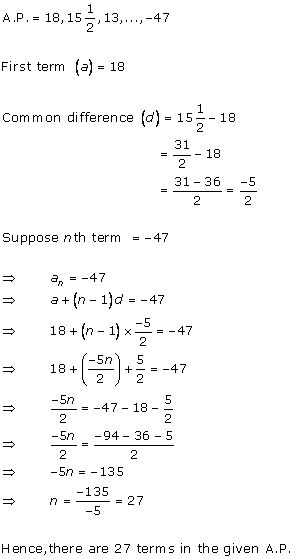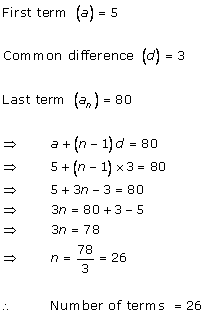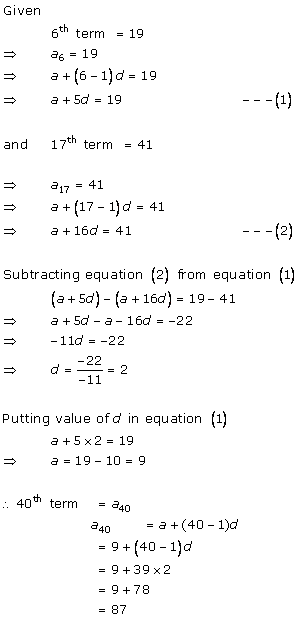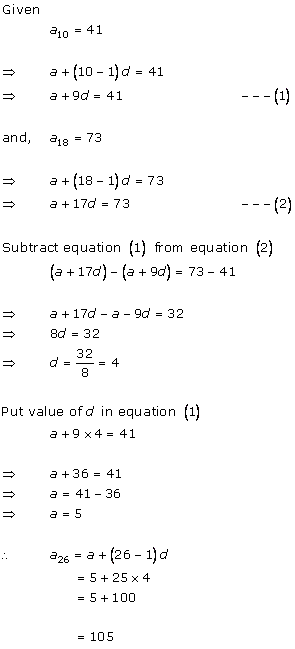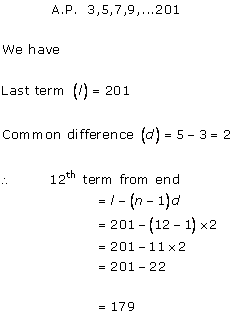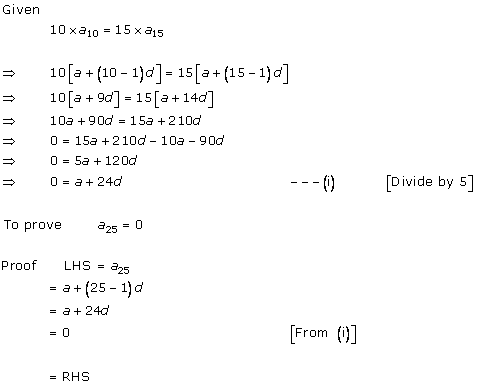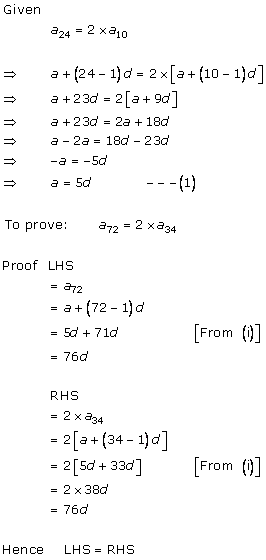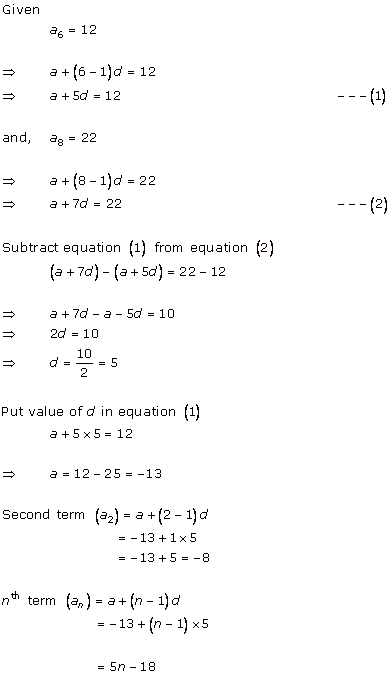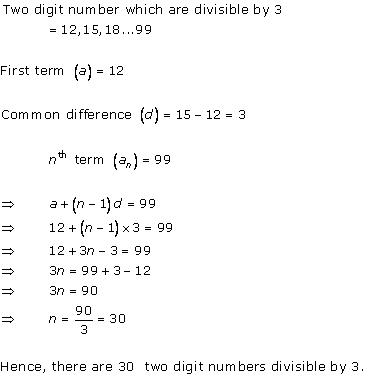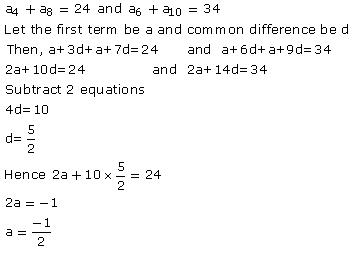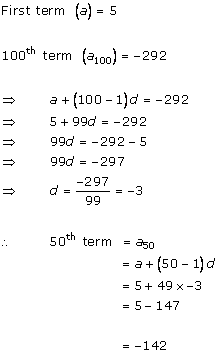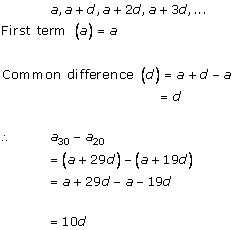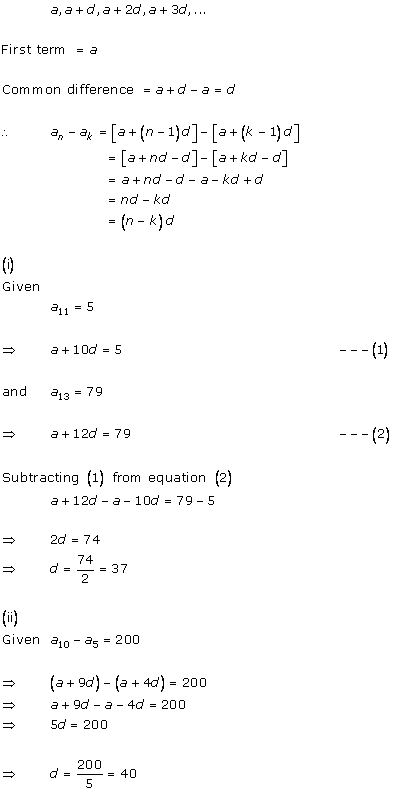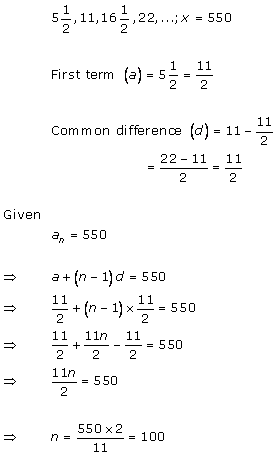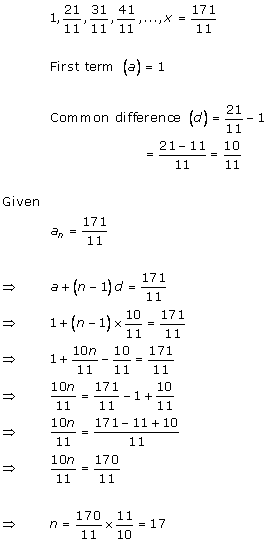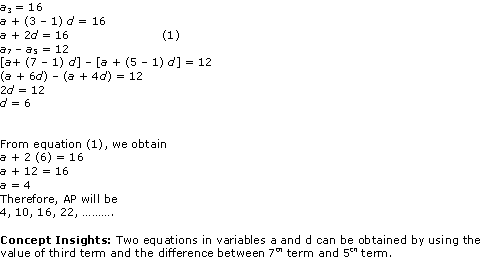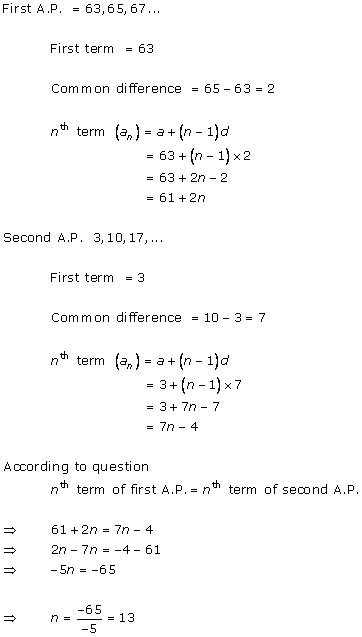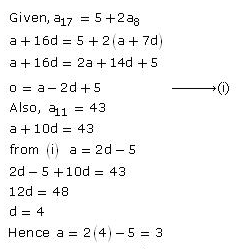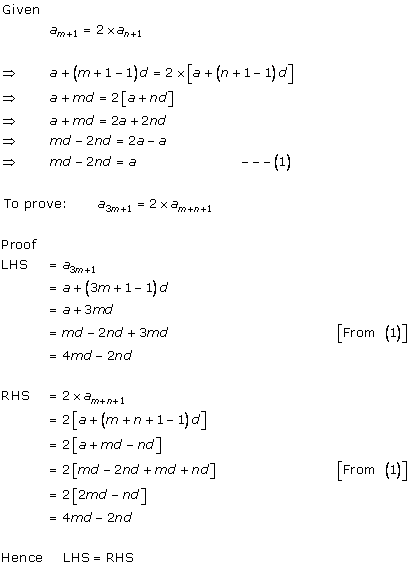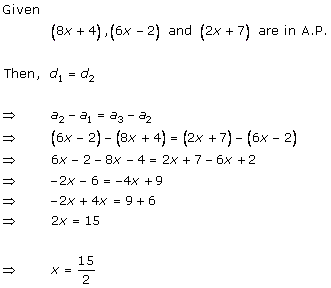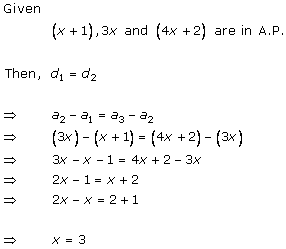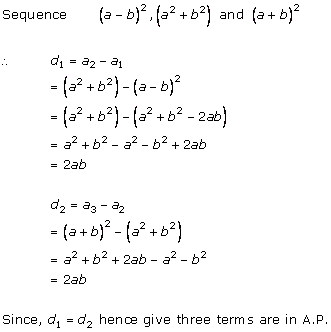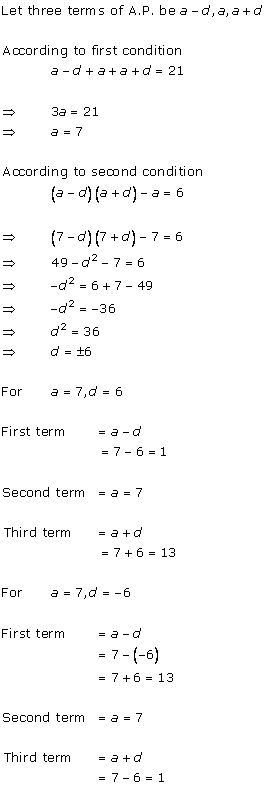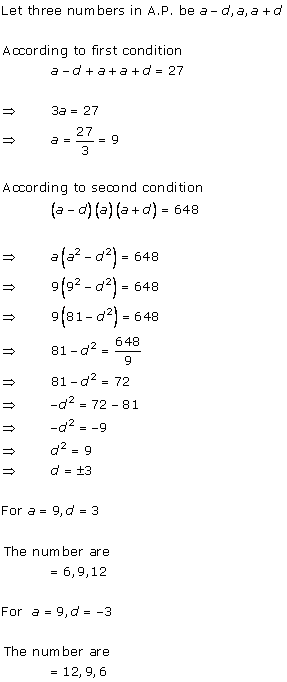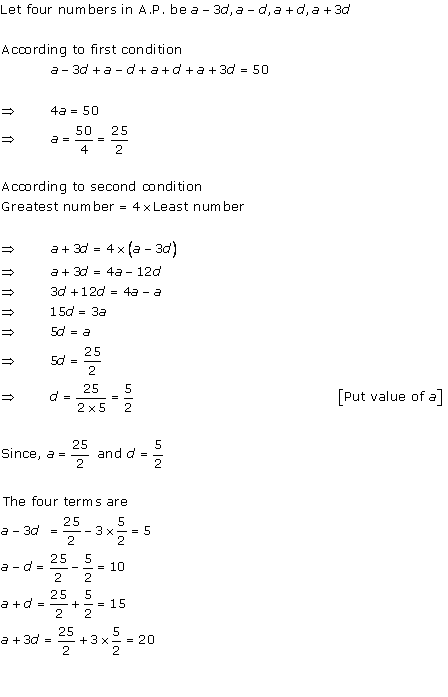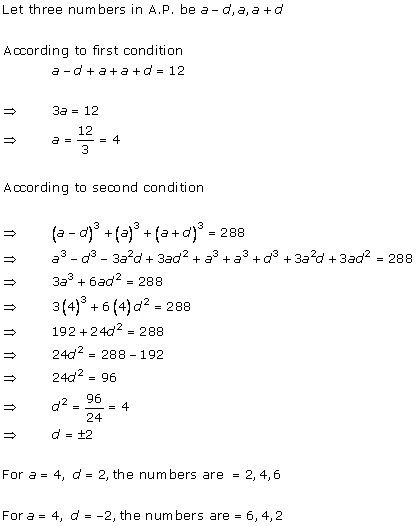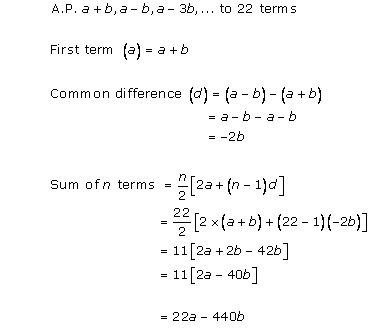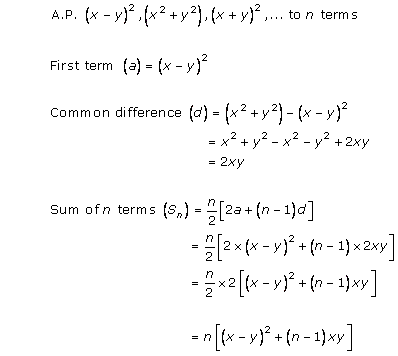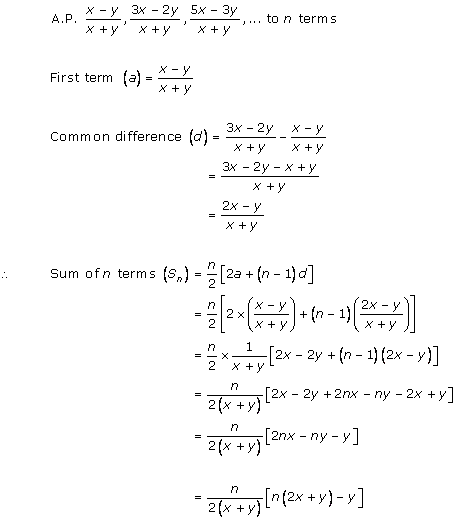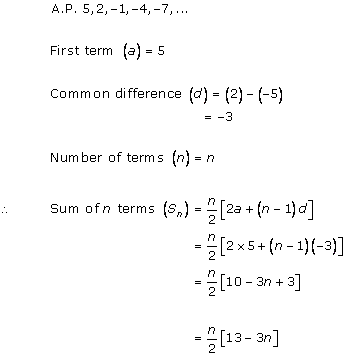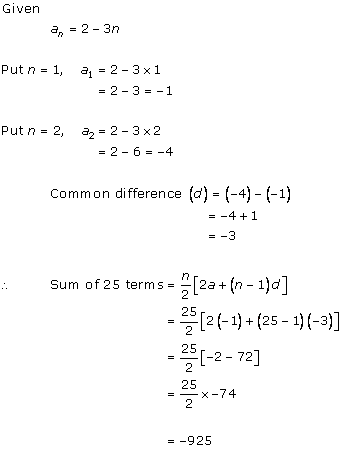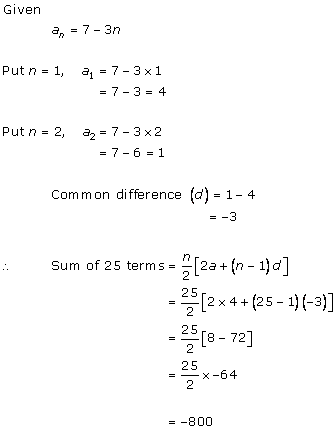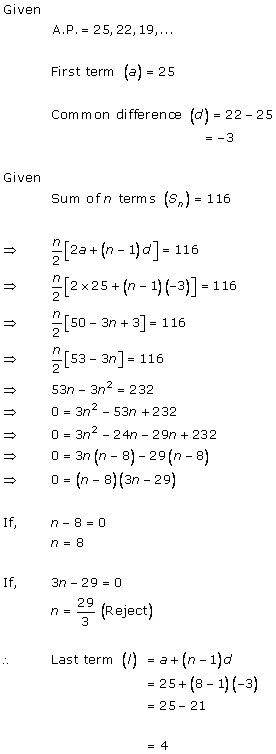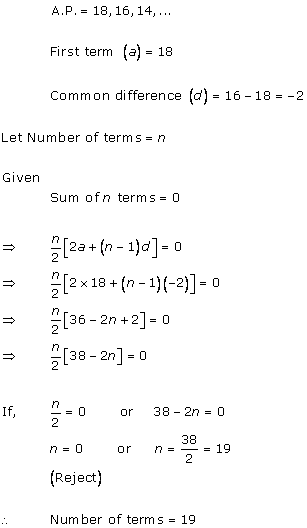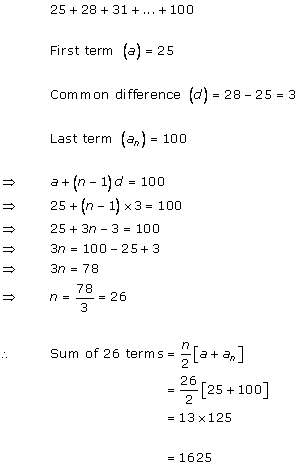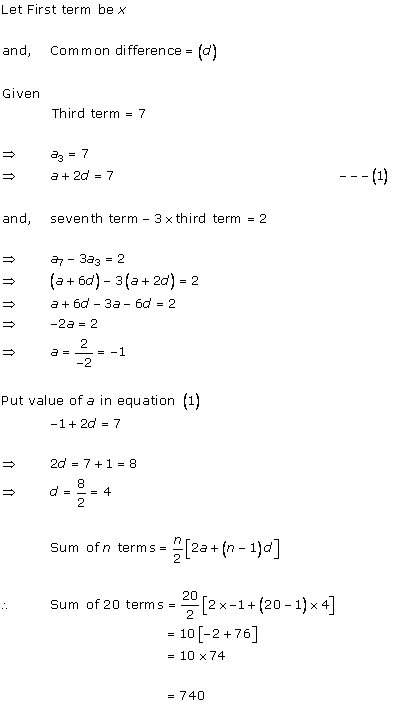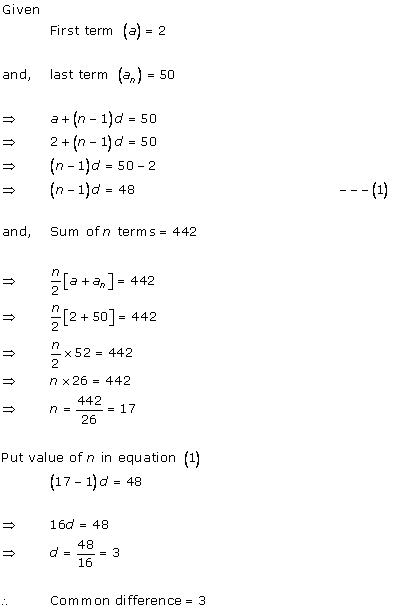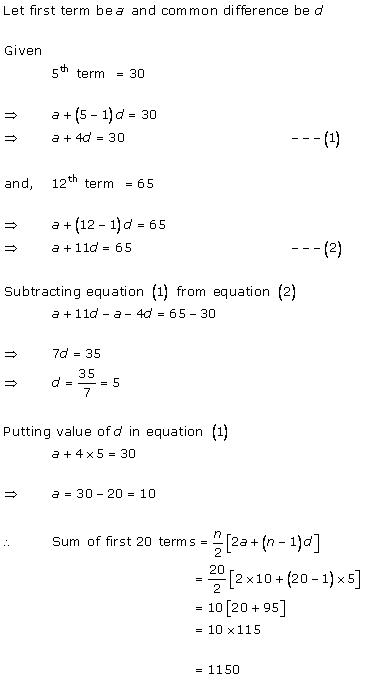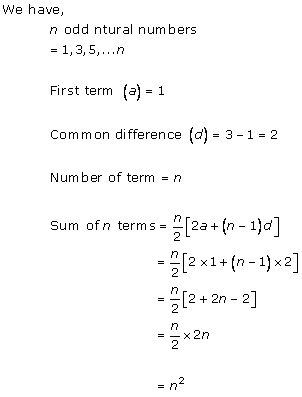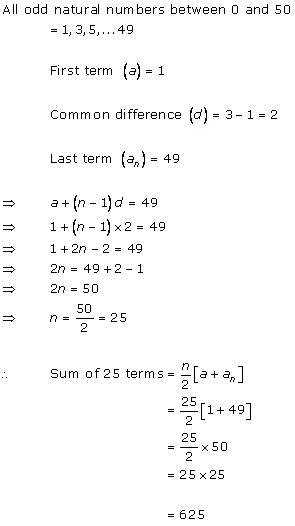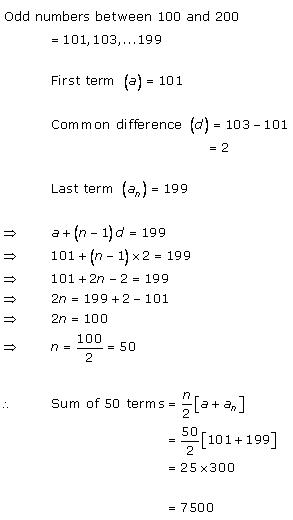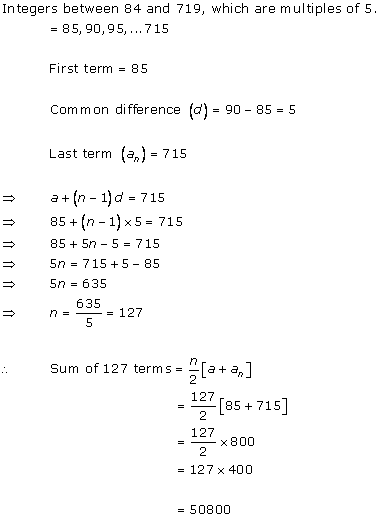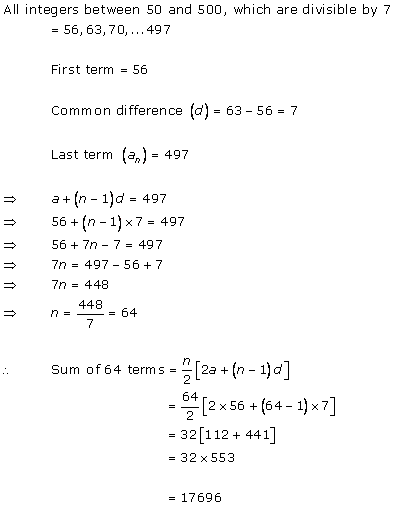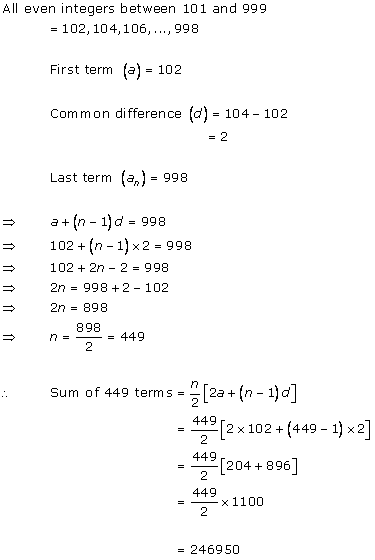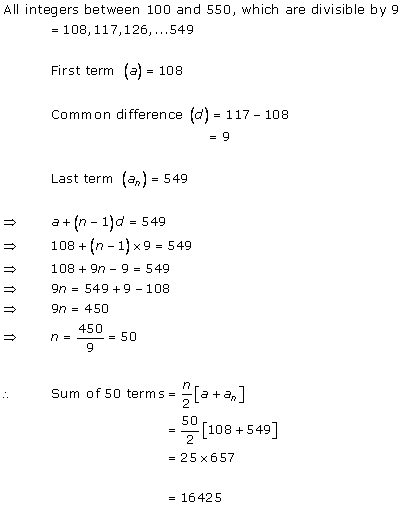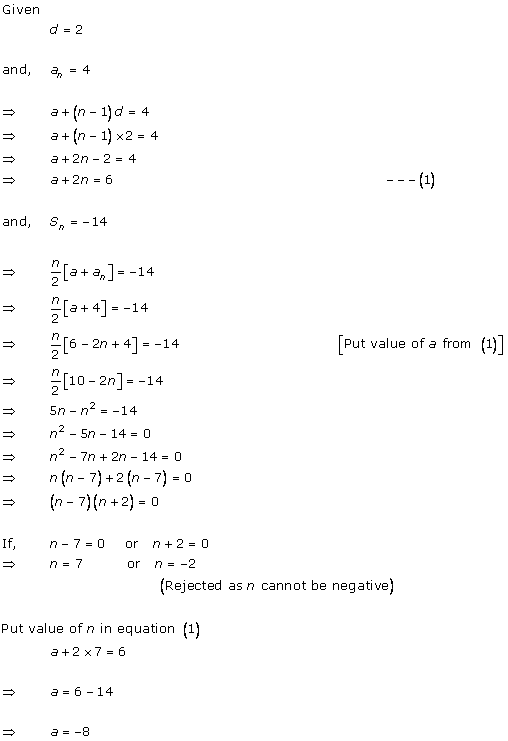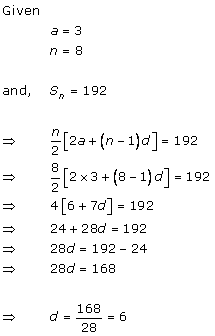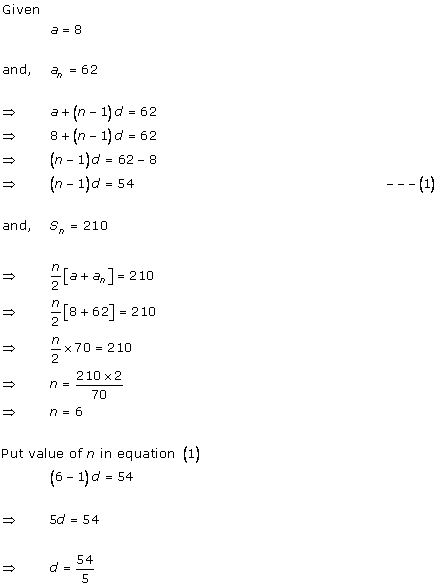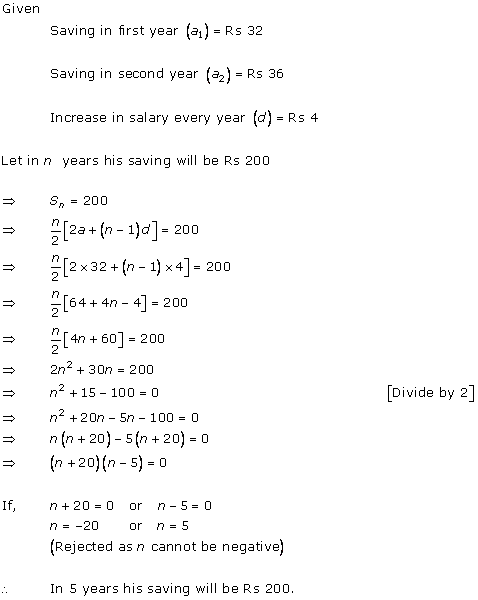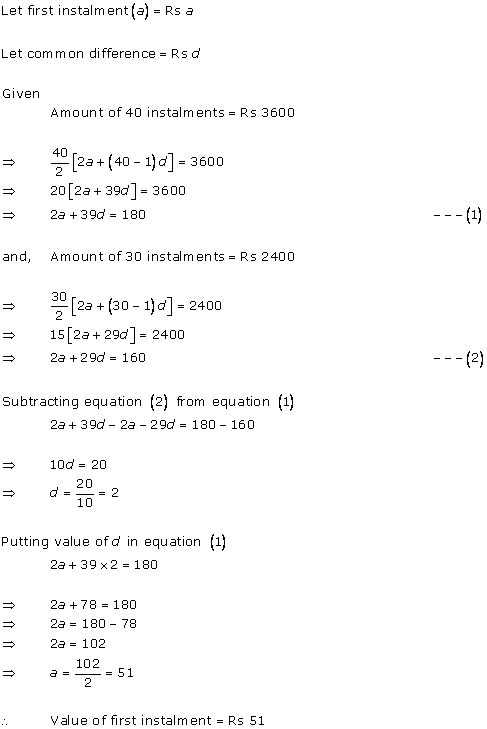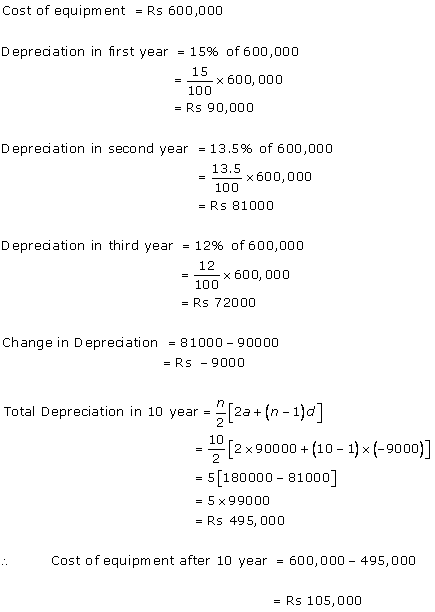Class 10 RD SHARMA Solutions Maths Chapter 5 - Arithmetic Progressions
Arithmetic Progressions Exercise Ex. 5.1
Solution 1 (i)
Solution 1 (ii)
Solution 1 (iii)
Solution 1 (iv)
Solution 1 (v)
Solution 1 (vi)
Solution 1 (vii)
Solution 1 (viii)
Solution 1 (ix)
Solution 2 (i)
Solution 2 (ii)
Solution 2 (iii)
Solution 2 (iv)
Solution 2 (v)
Solution 3 (i)
Solution 3 (ii)
Solution 3 (iii)
Solution 3 (iv)
Arithmetic Progressions Exercise Ex. 5.2
Solution 1
Solution 2
Solution 3
Solution 4 (i)
Solution 4 (ii)
Solution 4 (iii)
Solution 4 (iv)
Solution 5
Solution 6(i)

Solution 6(ii)

Solution 6(iii)

Arithmetic Progressions Exercise Ex. 5.3
Solution 1
Solution 2
Solution 3 (i)
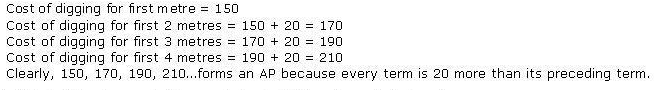
Solution 3 (ii)

Solution 3(iii)
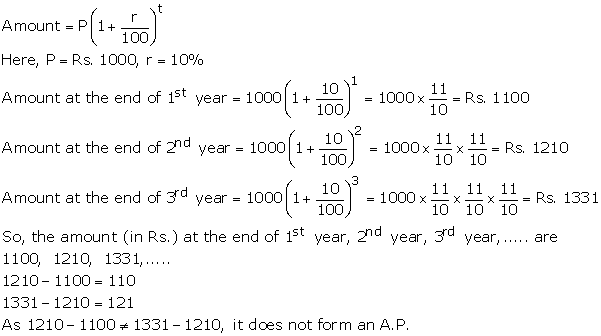
Solution 4 (i)
Solution 4 (ii)
Solution 4 (iii)
Solution 4 (iv)
Solution 5 (i)
Solution 5 (ii)
Solution 5 (iii)
Solution 5 (iv)
Solution 5 (v)
Solution 5 (vi)
Solution 5 (vii)
Solution 5 (viii)
Solution 5 (ix)
Solution 5 (x)
Solution 5 (xi)
Solution 5 (xii)
Solution 6
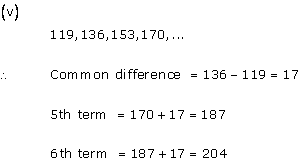
Solution 7
Arithmetic Progressions Exercise Ex. 5.4
Solution 1 (i)
Solution 1 (ii)
Solution 1 (iii)
Solution 1 (iv)
Solution 1 (v)
Solution 1 (vi)
Solution 1 (vii)
Solution 2 (i)
Solution 2 (ii)
Solution 2 (iii)
Solution 2 (iv)
Solution 2 (v)
Solution 2 (vi)
The given A.P. is -7, -12, -17, -22,…
First term (a) = -7
Common difference = -12 - (-7) = -5
Suppose nth term of the A.P. is -82.

So, -82 is the 16th term of the A.P.
To check whether -100 is any term of the A.P., take an as -100.

So, n is not a natural number.
Hence, -100 is not the term of this A.P.
Solution 3 (i)
Solution 3 (ii)
Solution 3 (iii)
Solution 4 (i)
Solution 4 (ii)
Solution 4 (iii)
Solution 4 (iv)
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9 (i)
Solution 9 (ii)
A.P. is 3, 8, 13, ..., 253
We have:
Last term (l) = 253
Common difference (d) = 8 - 3 = 5
Therefore,
12th term from end
= l - (n - 1)d
= 253 - (12 - 1) (5)
= 253 - 55
= 198
Solution 9 (iii)
Solution 10
Solution 11
Solution 12
Solution 13

Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20 (i)
Solution 20 (ii)
Solution 21
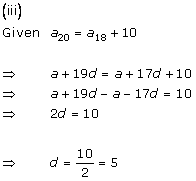
Solution 22 (i)
Solution 22 (ii)
Solution 22 (iii)
Solution 22 (iv)
Solution 23

Solution 24
Solution 25
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
Solution 31
Solution 32
Solution 33
Solution 34
Solution 35
Solution 36
Solution 37
Thus, nth term is given by
an = a + (n - 1)d
an = 3 + (n - 1)4
an = 3 + 4n - 4
an = 4n - 1
Solution 38
The smallest three digit number divisible by 9 = 108
The largest three digit number divisible by 9 = 999
Here let us write the series in this form,
108, 117, 126, …………….., 999
a = 108, d = 9
tn = a + (n - 1)d
999= 108 + (n - 1)9
⇒ 999 - 108 = (n - 1)9
⇒ 891 = (n - 1)9
⇒ (n - 1) = 99
⇒ n = 99 + 1
∴ n = 100
Number of terms divisible by 9
Number of all three digit natural numbers divisible by 9 is 100.
Solution 39
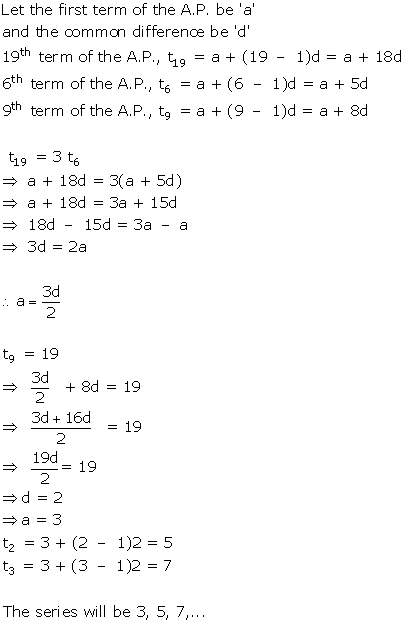
Solution 40
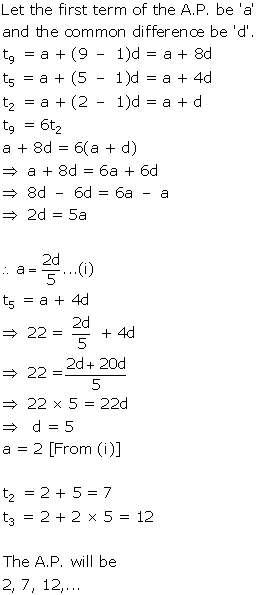
Solution 41
Let the first term be 'a' and the common difference be 'd'
t24 = a + (24 - 1)d = a + 23d
t10 = a + (10 - 1)d = a + 9d
t72 = a + (72 - 1)d = a + 71d
t15 = a + (15 - 1)d = a + 14d
t24 = 2t10
⇒ a + 23d = 2(a + 9d)
⇒ a + 23d = 2a + 18d
⇒ 23d - 18d = 2a - a
∴ 5d = a
t72 = a + 71d
= 5d + 71d
= 76d
= 20d + 56d
= 4 × 5d + 4 × 14d
= 4(5d + 14d)
= 4(a + 14d)
= 4t15
∴t72 = 4t15
Solution 42
L.C.M. of 2 and 5 = 10
3- digit number after 100 divisible by 10 = 110
3- digit number before 999 divisible by 10 = 990
Let the number of natural numbers be 'n'
990 = 110 + (n - 1)d
⇒ 990 - 110 = (n - 1) × 10
⇒ 880 = 10 × (n - 1)
⇒ n - 1 = 88
∴ n = 89
The number of natural numbers between 110 and 999 which are divisible by 2 and 5 is 89.
Solution 43
Let the first term be 'a' and the common difference be 'd'.
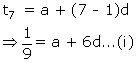
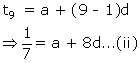

![]()
![]()
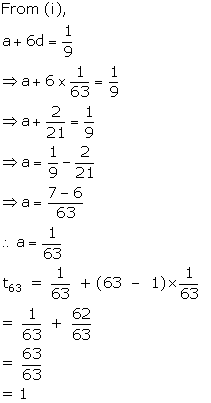
Solution 44

Solution 45
Let the first term be 'a' and the common difference be 'd'.
a = 40
d = 37 - 40 = - 3
Let the nth term of the series be 0.
tn = a + (n - 1)d
⇒ 0 = 40 + (n - 1)( - 3)
⇒ 0 = 40 - 3(n - 1)
⇒ 3(n - 1) = 40
![]()
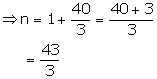
∴ No term of the series is 0.
Solution 46
Given A.P. is 213, 205, 197, …, 37.
Here, first term = a = 213
And, common difference = d = 205 - 213 = -8
an = 37
nth term of an A.P. is given by
an = a + (n - 1)d
⇒ 37 = 213 + (n - 1)(-8)
⇒ 37 = 213 - 8n + 8
⇒ 37 = 221 - 8n
⇒ 8n = 221 - 37
⇒ 8n = 184
⇒ n = 23
So, there are 23 terms in the given A.P.
⇒ The middle term is 12th term.
⇒ a12 = 213 + (12 - 1)(-8)
= 213 + (11)(-8)
= 213 - 88
= 125
Hence, the middle term is 125.
Solution 47
Let a be the first term and d be the common difference of the A.P.
Then, we have
a5 = 31 and a25 = a5 + 140
⇒ a + 4d = 31 and a + 24d = a + 4d + 140
⇒ a + 4d = 31 and 20d = 140
⇒ a + 4d = 31 and d = 7
⇒ a + 4(7) = 31 and d = 7
⇒ a + 28 = 31 and d = 7
⇒ a = 3 and d = 7
Hence, the A.P. is a, a + d, a + 2d, a + 3d, ……
i.e. 3, 3 + 7, 3 + 2(7), 3 + 3(7), ……
i.e. 3, 10, 17, 24, …..
Solution 48

Solution 49
Solution 50
Solution 51

Solution 52

Solution 53
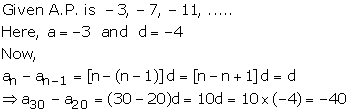
Solution 54

Arithmetic Progressions Exercise Ex. 5.5
Solution 1
Solution 2
Solution 3
Solution 5
Solution 4
Solution 6
Solution 7
Solution 8

Solution 9
Let the first three terms of an A.P. be a - d, a, a + d
As per the question,
(a - d) + a + (a + d) = 18
∴ 3a = 18
∴ a = 6
Also, (a - d)(a + d) = 5d
∴ (6 - d)(6 + d) = 5d
∴ 36 - d2 = 5d
∴ d2 + 5d - 36 = 0
∴ d2 + 9d - 4d - 36 = 0
∴ (d + 9)(d - 4) = 0
∴ d = -9 or d = 4
Thus, the terms will be 15, 6, -3 or 2, 6, 10.
Solution 10

Solution 11

Solution 12

Arithmetic Progressions Exercise Ex. 5.6
Solution 1 (i)
Solution 1 (ii)
Solution 1 (iii)
Solution 1 (iv)
Solution 1 (v)
Solution 1 (vi)
Solution 1 (vii)
Solution 1 (viii)
Solution 2
Solution 3
Solution 4

Solution 5 (i)
Solution 5 (ii)
Solution 5 (iii)
Solution 5 (iv)
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10 (i)
Solution 10 (ii)
Solution 10 (iii)
Solution 10 (iv)
Solution 10(v)

Solution 11 (i)
Solution 10 (vi)
Let the required number of terms be n.
As the given A.P. is 45, 39, 33 …
Here, a = 45 and d = 39 - 45 = -6
The sum is given as 180
∴ Sn = 180

When n = 10,
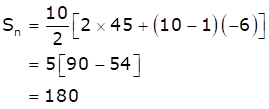
When n = 6,
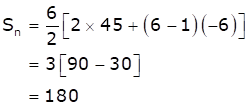
Hence, number of terms can be 6 or 10.
Solution 11 (ii)
Solution 11 (iii)
Solution 12(i)
Multiples of 8 are8,16,24,…
Now,
n=15, a=8, d=8
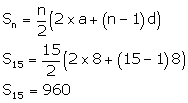
Solution 12(ii)
a)
divisible by 3
3,6,9,…
Now,
n=40, a=3, d=3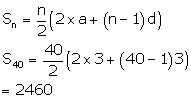
b)
divisible by 5
5,10,15,…
Now,
n=40, a=5, d=5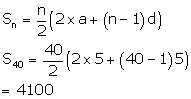
c)divisible by 6
6,12,18,…
Now,
n=40, a=3, d=6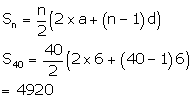
Solution 12(iii)
Three-digit numbers divisible by 13 are 104,117,
130,…988.
Now,
a=104, l=988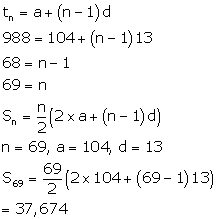
Solution 12(iv)
Three-digit numbers which are multiples
of 11 are 110,121, 132,…990.
Now,
a=110, l=990
Solution 12(v)
Two-digit numbers divisible by 4 are 12,16,…96.
Now,
a=12, l=96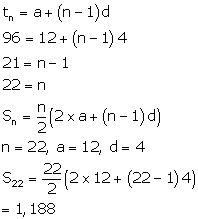
Solution 12 (vi)
The multiples of 3 are 3, 6, 9, 12, 15, 18, 21, …
These are in A.P. with,
first term (a) = 3 and common difference (d) = 3
To find S8 when a = 3, d = 3
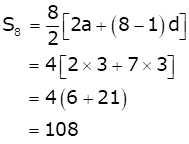
Hence, the sum of first 8 multiples of 3 is 108.
Solution 13 (i)
Solution 13 (ii)
Solution 13 (iii)
Solution 13 (iv)
Solution 13 (v)
Solution 13 (vi)
Solution 13 (vii)
Solution 13 (viii)
Let 'a' be the first term and 'd' be the common difference.
![]()
tn = a + (n - 1)d

Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
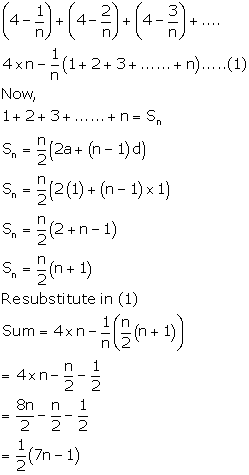
Solution 19
Solution 20
Solution 21
Solution 22 (i)
Solution 22 (ii)
Sum of first n terms of an AP is given by
![]()
As per the question, S4 = 40 and S14 = 280
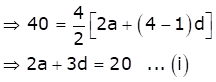
Also, ![]()
![]()
Subtracting (i) from (ii), we get, 10d = 20
Therefore, d = 2
Substituting d in (i), we get, a = 7
Sum of first n terms becomes
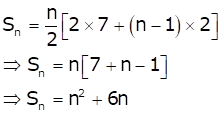
Solution 23
Solution 24
Solution 25
Solution 26
Let the number of terms be 'n', 'a' be the first term and 'd' be the common difference.
tn = a + (n - 1)d
⇒ 49 = 7 + (n - 1)d
⇒ 42 = (n - 1)d…..(i)
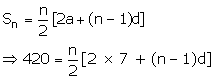
∴ 840 = n[14 + (n - 1)d]……(ii)
Substituting (ii) in (i),
840 = n[14 + 42]
⇒ 840 = 56n
∴ n = 15
Substituting n in (i)
42 = (15 - 1)d
![]()
Common difference, d =3
Solution 27
Let the number of terms be 'n', 'a' be the first term and 'd' be the common difference.
tn = a + (n - 1)d
⇒ 45 = 5 + (n - 1)d
⇒ 40 = (n - 1)d…..(i)
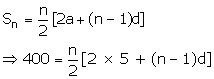
∴ 800 = n[10 + (n - 1)d]……(ii)
Substituting (ii) in (i),
800 = n[10 + 40]
⇒ 800 = 50n
∴ n = 16
Substituting n in (i)
40 = (16 - 1)d

Solution 28

Solution 29
Let 'a' be the first term and 'd' be the common difference.
tn = a + (n - 1)d
![]()
t10 = a + (10 - 1)d
⇒ 21 = a + 9d……(i)
![]()
120 = 5[2a + 9d]
24 = 2a + 9d………(ii)
(ii) - (i) ⇒
a = 3
Substituting a in (i), we get
a + 9d = 21
⇒ 3 + 9d = 21
⇒ 9d = 18
∴d = 2
tn = a + (n - 1)d
= 3 + (n - 1)2
= 3 + 2n - 2
∴ tn= 2n + 1
Solution 30
Let the first term be 'a' and the common difference be 'd' 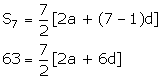
63 = 7[a + 3d]
9 = a + 3d……….(i)
Sum of the next 7 terms = 161
Sum of the first 14 terms = 63 + 161 = 224
![]()
224 = 7[2a + 13d]
32 = 2a + 13d………..(ii)
Solving (i) and (ii), we get
d = 2, a = 3
28th term of the A.P., t28 = a + (28 - 1)d
= 3 + 27 × 2
= 3 + 54
= 57
∴ The 28th of the A.P. is 57.
Solution 31
Let the first term be 'a' and the common difference be 'd'.
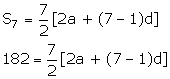
26 × 2 = [2a + (7 - 1)d]
52 = 2a + 6d
26 = a + 3d……..(i)

From (i) and (ii),
⇒ 13d = 104
∴d = 8
From (i), a = 2
The A.P. is 2, 10, 18, 26,…….
Solution 32
Let the first term of the A.P. be 'a' and the common difference be 'd'.
tn = - 4n + 15
t1 = - 4 × 1 + 15 = 11
t2 = - 4 × 2 + 15 = 7
t3 = - 4 × 3 + 15 = 3
Common Difference, d = 7 - 11 = -4

= 10 × (-54)
= - 540
*Note: Answer given in the book is incorrect.
Solution 33
Solution 34
Solution 35
Solution 36
Solution 37
Let the number of the terms be 'n'.
Common Difference, d = - 9 + 12 = 3
tn = a + (n - 1)d
⇒ 21 = - 12 + 3(n - 1)
⇒ 21 + 12 = 3(n - 1)
⇒ 3(n - 1) = 33
⇒ n - 1 = 11
∴n = 12
Number of terms of the series = 12
If 1 is added to each term of the above A.P.,
- 11, - 8, - 5,…….,22
Number of terms in the series, n1 = 12
Sum of all the terms,
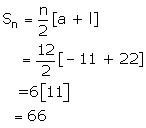
The sum of the terms = 66
Solution 38
Sum of n terms of the A.P., Sn = 3n2 + 6n
S1 = 3 × 12 + 6 × 1 = 9 = t1 ……(i)
S2 = 3 × 22 + 6 × 2 = 24 = t1 + t2 …….(ii)
S3 = 3 × 32 + 6 × 3 = 45 = t1 + t2 + t3 ……..(iii)
From (i), (ii) and (iii),
t1 = 9, t2 = 15, t3 = 21
Common difference, d = 15 - 9 = 6
nth of the AP, tn = a + (n - 1)d
= 9 + (n - 1) 6
= 9 + 6n - 6
= 6n + 3
Thus, the nth term of the given A.P. = 6n + 3
Solution 39
Sn = 5n - n2
S1 = 5 × 1 - 12 = 4 = t1………..(i)
S2 = 5 × 2 - 22 = 6 = t1 +t2………..(ii)
S3 = 5 × 3 - 32 = 6 = t1 + t2 + t3……….(iii)
From (i), (ii) and (iii),
t1 = 4, t2 = 2, t3 = 0
Here a = 4, d = 2 - 4 = - 2
tn = a + (n - 1)d
= 4 + (n - 1)( -2)
= 4 - 2n + 2
= 6 - 2n
Solution 40
Sn = 4n2 + 2n
S1 = 4 × 12 + 2 × 1 = 6 = t1………….(i)
S2 = 4 × 22 + 2 × 2 = 20 = t1 + t2……….(ii)
S3 = 4 × 32 + 2 × 3 = 42 = t1 + t2 + t3………..(iii)
From (i), (ii) and (iii),
t1 = 6, t2 = 14, t3 = 22
Here a = 6, d = 14 - 6 = 8
tn = a + (n - 1)d
tn = 6 + (n - 1)8
= 6 + 8n - 8
= 8n - 2
*Note: Answer given in the book is incorrect.
Solution 41
Sum of n terms of the A.P., Sn = 3n2 + 4n
S1 = 3 × 12 + 4 × 1 = 7 = t1………(i)
S2 = 3 × 22 + 4 × 2 = 20 = t1 + t2…….(ii)
S3 = 3 × 32 + 4 × 3 = 39 = t1 + t2 + t3 …….(iii)
From (i), (ii), (iii)
t1 = 7, t2 = 13, t3 = 19
Common difference, d = 13 - 7 = 6
25th of the term of this A.P., t25 = 7 + (25 - 1)6
= 7 + 144 = 151
∴The 25th term of the A.P. is 151.
Solution 42
Sum of the terms, Sn = 5n2 + 3n
S1 = 5 × 12 + 3 × 1 = 8 = t1………..(i)
S2 = 5 × 22 + 3 × 2 = 26 = t1 + t2…………..(ii)
S3 = 5 × 32 + 3 × 3 = 54 = t1 + t2 + t3…………(iii)
From(i), (ii) and (iii),
t1 = 8, t2 = 18, t3 = 28
Common difference, d = 18 - 8 = 10
tm = 168
⇒ a + (m - 1)d = 168
⇒ 8 + (m - 1)×10 = 168
⇒ (m - 1) × 10 = 160
⇒ m - 1 = 16
∴m = 17
t20 = a + (20 - 1)d
= 8 + 19 × 10
= 8 + 190
= 198
Solution 43
Let the first term be 'a' and the common difference be 'd'.
Sum of the first 'q' terms, Sq = 63q - 3q2
S1 = 63 × 1 - 3 × 12 = 60 = t1……..(i)
S2 = 63 × 2 - 3 × 22 = 114 = t1 + t2…..(ii)
S3 = 63 × 3 - 3 × 32 = 162 = t1 + t2 + t3 .....(iii)
From (i), (ii) and (iii),
t1 = 60
t2 = 54
t3 = 48
Common difference, d = 54 - 60 = - 6
tp = a + (p - 1)d
⇒ -60 = 60 + (p - 1)( - 6)
⇒ - 120 = - 6(p - 1)
⇒ p - 1 = 20
∴p = 21
t11 = 60 + (11 - 1)( - 6)
=60 + 10( - 6)
= 60 - 60
= 0
The 11th term of the A.P. is 0.
Solution 44
Let the first term of the A.P. be 'a' and the common difference be 'd'
Sum of m terms of the A.P., Sm = 4m2 - m
S1 = 4 × 12 - 1 = 3 = t1 …….(i)
S2 = 4 × 22 - 2 = 14 = t1 + t2……..(ii)
S3 = 4 × 32 - 3 = 33 = t1 + t2 + t3 …….(iii)
From (i), (ii) and (iii)
t1 = 3, t2 = 11, t3 = 19
Common difference, d = 11 - 3 = 8
tn = 107
⇒ a + (n - 1)d = 107
⇒ 3 + (n - 1)8 = 107
⇒ 8(n - 1) = 104
⇒ n - 1 = 13
∴n = 14
t21 = 3 + (21 - 1)8 = 3 + 160 = 163
Solution 45
Solution 46

Solution 47 (i)
Solution 47 (ii)
Sum of first n terms of an AP is given by
![]()
As per the question, Sn = n2
![]()
![]()
![]()
Hence, the 10th term of this A.P. is 19.
Solution 48
Solution 49
Solution 50 (i)
Solution 50 (ii)
Solution 51
Solution 52
Solution 53
Solution 54
Solution 55 (i)
Solution 55(ii)

Solution 55(iii)

Solution 55(iv)

Solution 55(v)




Solution 56 (i)
Solution 56 (ii)
Solution 56 (iii)
Solution 56 (iv)
Solution 56 (v)
Solution 56 (vi)
Solution 56(vii)
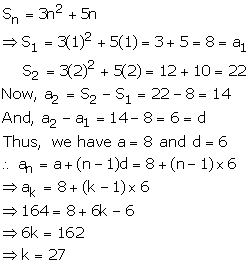
Solution 56 (viii)
The nth term of an A.P. is given by an = a + (n - 1)d
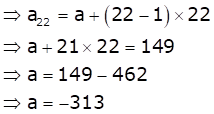
Sum of first n terms of an AP is given by
![]()
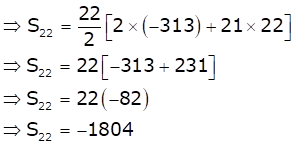
Solution 57
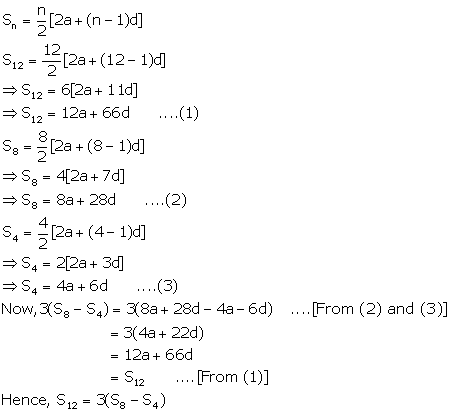
Solution 58

Solution 59

Solution 60

Solution 61
Trees planted by the student in class 1 = 2 + 2 = 4
Trees planted by the student in class 2 = 4 + 4 = 8
Trees planted by the students in class 3 = 6 + 6 = 12
…….
Trees planted by the students in class 12 = 24 + 24 = 48
∴ the series will be 4, 8, 12,………., 48
a = 4, Common Difference, d = 8 - 4 = 4
Let 'n' be the number of terms in the series.
48 = 4 + (n - 1)4
⇒ 44 = 4(n - 1)
⇒ n - 1 = 11
∴n = 12
Sum of the A.P. series,

Number of trees planted by the students = 312
Solution 62
Since, the difference between the savings of two consecutive months is Rs. 20, therefore the series is an A.P.
Here, the savings of the first month is Rs. 50
First term, a = 50, Common difference, d = 20
No. of terms = no. of months
No. of terms, n = 12
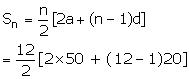
= 6[100 + 220]
= 6×320
= 1920
After a year, Ramakali will save Rs. 1920.
Yes, Ramakali will be able to fulfill her dream of sending her daughter to school.
Solution 63
Solution 64
Solution 65
Solution 66
Solution 67
Solution 68
Solution 69
Solution 70
Let the first term of the A.P. be 'a' and the common difference be 'd'.
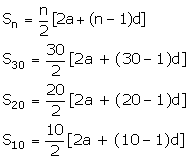
R.H.S.
= 3(S20 - S10)
![]()
= 3(10[2a + 19d] - 5[2a + 9d])
= 3(20a + 190d - 10a - 45d)
= 3(10a + 145d)
= 3 × 5(2a + 29d)
= 15[2a + (30 - 1)d]
![]()
= S30
= L.H.S.
Solution 71
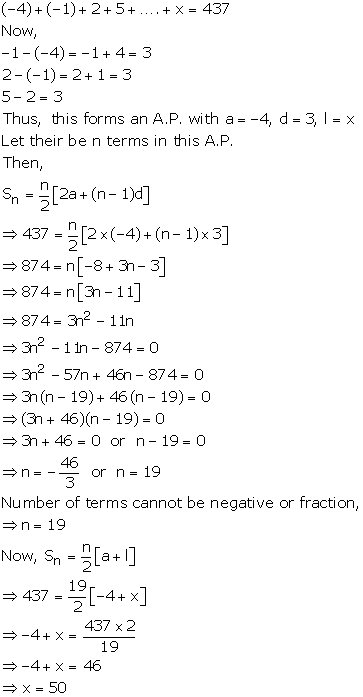
Solution 72

Solution 73
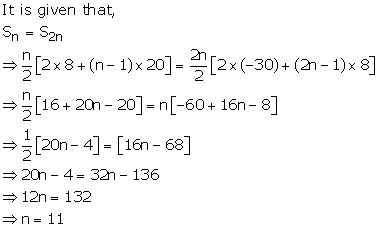
Solution 74


Arithmetic Progressions Exercise Ex. MCQs
Solution 1
The nth term of an A.P. is given by an = a + (n - 1)d
As per the question, a7 = 34 and a13 = 64
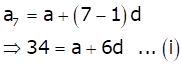
Also, ![]()
![]()
Subtracting (i) from (ii), we get, 6d = 30
Therefore, d = 5
Substituting a in (i), we get, a = 4
The 18th term is
a18 = a + 17d
= 4 + 85
= 89
Thus, the 18th term is 89.
Hence, option (c) is correct.
Solution 2
The sum of first n terms of an A.P. is given by
![]()
As per the question, ![]()
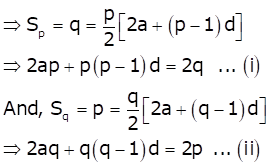
Subtracting (ii) from (i), we get
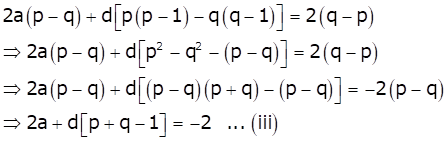
Now, sum of (p + q) terms is
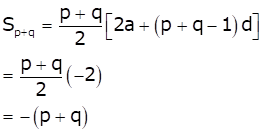
Hence, option (d) is correct.
Solution 3
Given: Sn = 3n2 + n and d = 6
![]()
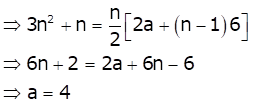
Thus, the first term is 4.
Hence, option (d) is correct.
Solution 4
Given: First term (a) = 1, last term (l) = 11 and Sn = 36
We know that, sum of n terms is given by ![]()
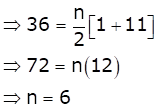
Thus, the number of terms is 6.
Hence, option (b) is correct.
Solution 5
Given: Sum of n terms Sn = 3n2 + 5n
For n = 1, we get
S1 = 3(1)2 + 5(1) = 8
For n = 2, we get
S2 = 3(2)2 + 5(2) = 22
We know that, an = Sn - Sn - 1
![]()
Therefore, we have
Common difference (d) = 14 - 8 = 6
Let 164 be the nth term of this A.P.
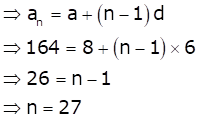
Thus, 164 is the 27th term of this A.P.
Hence, option (b) is correct.
Solution 6
Given: Sum of n terms Sn = 2n2 + 5n
For n = 1, we get
S1 = 2(1)2 + 5(1) = 7
For n = 2, we get
S2 = 2(2)2 + 5(2) = 18
We know that, an = Sn - Sn - 1
![]()
Here, common difference (d) = 11 - 7 = 4
The nth term is given by
an = a + (n - 1)d
= 7 + (n - 1)(4)
= 4n + 3
Thus, the nth term is 4n + 3.
Hence, option (c) is correct.
Solution 7
Let (a - d), a and (a + d) be the first three consecutive terms of an A.P.
As per the question, we have
(a - d) + a + (a + d) = 51
i.e. 3a = 51
i.e. a = 17
Also, (a - d)(a + d) = 273
(a2 - d2) = 273
289 - d2 = 273
d2 = 289 - 273
d2 = 16
d = ± 4
As the series is an increasing A.P., d must be positive.
Therefore, d = 4
So, we get, a + d = 21
Hence, option (c) is correct.
Solution 8
Let (a - 3d), (a - d), (a + d) and (a + 3d) be the four numbers of an A.P.
As per the question, we have
(a - 3d) + (a - d) + (a + d) + (a + 3d) = 50
i.e. 4a = 50
i.e. a = 12.5
Also, a + 3d = 4(a - 3d)
i.e. a + 3d = 4a - 12d
i.e. 3a = 15d
i.e. a = 5d
i.e. 5d = 12.5
Therefore, d = 2.5
So, (a - 3d) = 5, (a - d) = 10, (a + d) = 15 and (a + 3d) = 20.
Thus, the numbers are 5, 10, 15 and 20.
Hence, option (a) is correct.
Solution 9
Let a be the first term.
Sum of n terms of an A.P. is given by
![]()
So, the sum of (n - 1) terms is
![]()
And, sum of (n - 2) terms is
![]()
As it is given that d = Sn - kSn-1 + Sn-2, we have
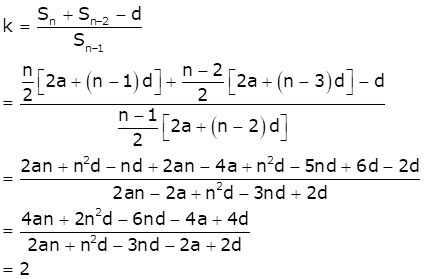
Hence, option (b) is correct.
Solution 10
Sum of n terms of an A.P. is given by
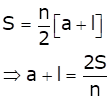
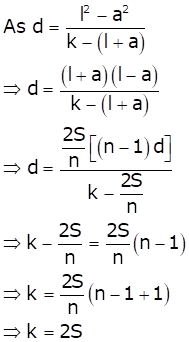
Hence, option (b) is correct.
Solution 11
The n even natural numbers 2, 4, 6,… forms an A.P. with first terms 2 and common difference 2.
So, the sum of first n even natural numbers is given by
![]()
The n odd natural numbers 1, 3, 5,… forms an A.P. with first terms 1 and common difference 2.
So, the sum of first n odd natural numbers is given by
![]()
As per the question,
Se = k So
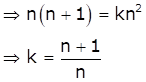
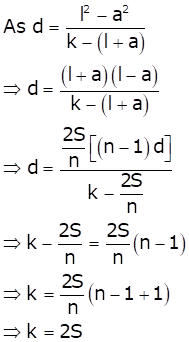
Hence, option (b) is correct.
Solution 12
Given: First term = a, second term = b and last term = 2a
Therefore, common difference (d) = b - a
As the last term is 2a, we have
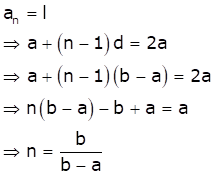
The of all the terms is given by
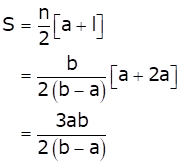
Hence, option (c) is correct.
Solution 13
Sum of 'n' odd number of terms of an A.P. is
![]()
![]()
Therefore, we have
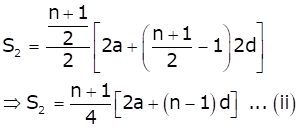
From equations (i) and (ii), we get
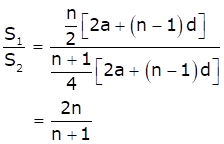
Hence, option (a) is correct.
Solution 14
We know that, sum of n terms of an A.P. is given by
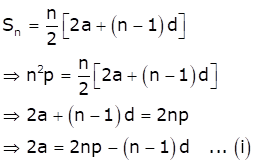
Also, ![]()
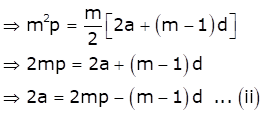
From (i) and (ii), we get
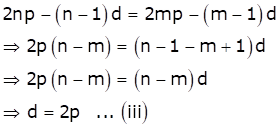
From (i), we get
2a = 2np - (n - 1)2p
i.e. 2a = 2np - 2np +2p
i.e. a = p
Now, the sum of p terms Sp is

Hence, option (c) is correct.
Solution 15
We know that, sum of n terms of an A.P. is given by
![]()
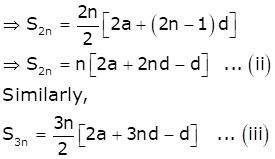
As S2n = 3Sn, we have
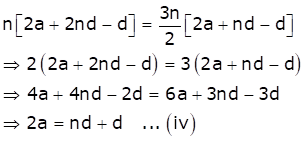
Consider,

Thus, S3n : Sn = 6.
Hence, option (b) is correct.
Solution 16
Given: ![]()
The sum of first n terms of an A.P. is given by
![]()
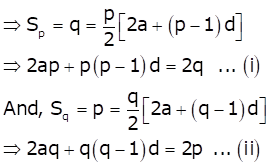
Subtracting (ii) from (i), we get
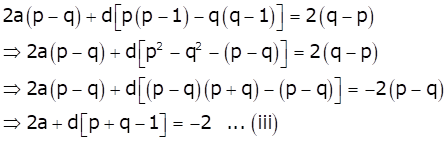
Therefore, Sp+q is
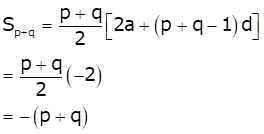
Hence, option (b) is correct.
Solution 17
Given: ![]()
The sum of first n terms of an A.P. is given by
![]()
Therefore, S3n will be
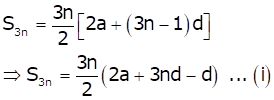
Similarly,
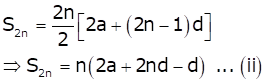
From (i), (ii) and (iii), we have
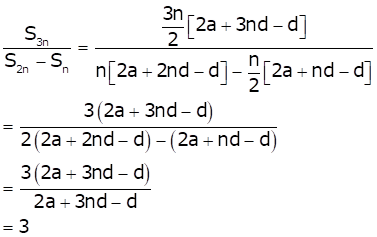
Thus, ![]()
Hence, option (c) is correct.
Solution 18
Given: First term (a) = 2 and common difference (d) = 4
The sum of first n terms of an A.P. is given by
![]()
Sum of its 40 terms will be
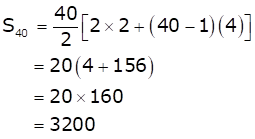
Hence, option (a) is correct.
Solution 19
In the given A.P. 3, 7, 11, 15, … we have
First term (a) = 3 and common difference (d) = 4
The sum of first n terms of an A.P. is given by
![]()
As the sum is given as 406, we have
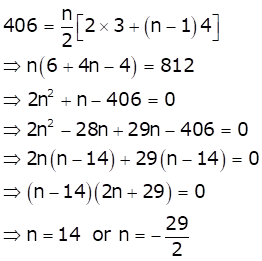
Since the number of terms can't be negative, so n = 14.
Hence, option (d) is correct.
Solution 20
For the given series, the terms![]() forms an A.P.
forms an A.P.
Here, first term (a) = ![]() and common
difference (d) =
and common
difference (d) = ![]()
The sum of first n terms of an A.P. is given by
![]()
Therefore, sum of the series is
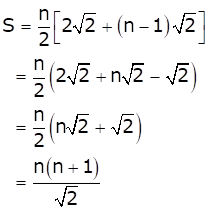
Hence, option (c) is correct.
Solution 21
In an A.P., a9 = 449 and a449 = 9
We know that the nth term is given by
an = a + (n - 1)d
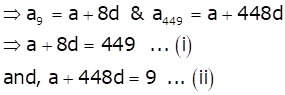
Subtracting (ii) from (i), we get
-440d = 440
Therefore, d = -1
Putting the value of d in (i), we get
a - 8 = 449
Therefore, a = 457
Let nth term be 0 i.e. an = 0

Hence, option (c) is correct.
Solution 22
As ![]() are in A.P.
are in A.P.
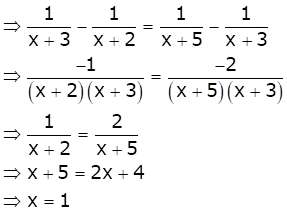
Hence, option (c) is correct.
Solution 23
Let the A.P. be a1, a2, a3, …
As Sn is the sum of n terms of an A.P., we have
Sn = a1 + a2 + a3 + … + an
∴ Sn-1 = a1 + a2 + a3 + … + an-1
Sn - Sn-1 = a1 + a2 + a3 + … + an-1 + an - (a1 + a2 + a3 + … + an-1)
= an
Thus, Sn - Sn-1 = an.
Hence, option (b) is correct.
Solution 24
Let the A.P. be a1, a2, a3, …
When Sn is the sum of n terms of an A.P., nth term will be
an = Sn - Sn-1
Similarly,
an-1 = Sn-1 - S(n-1) - 1 = Sn-1 - Sn-2
Now, the common difference is given by
d = an - an-1
= Sn - Sn-1 - (Sn-1 - Sn-2)
= Sn - 2Sn-1 + Sn-2
Hence, option (a) is correct.
Solution 25
Let Sn and S'n denotes the sum of first n terms of the two APs respectively.
![]()
Ratio of the sum of two APs is
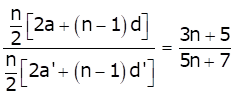
Replacing n with (2n - 1), we get
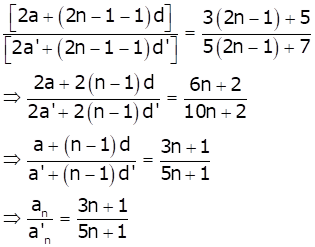
Hence, option (b) is correct.
Solution 26
As Sn is the sum of n terms of an A.P., we have
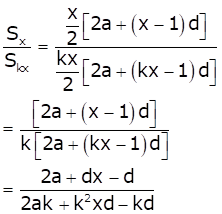
As ![]() is independent of x,
then
is independent of x,
then
2a - d = 0
i.e. 2a = d
Putting this in the ratio, we get
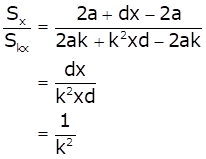
Thus, 2a = d.
Hence, option (b) is correct.
Solution 27
The nth term of an A.P. is given by an = a + (n - 1)d
Here, 'a' and 'd' are first term and common difference
As b is the nth term of an A.P., we have
b = a + (n - 1)d
b - a = (n - 1)d
![]()
Hence, option (b) is correct.
Solution 28
The n odd natural numbers are 1, 3, 5, … n.
These terms forms an A.P. with first term (a) = 1 and common difference (d) = 2.
So, the sum of first n odd natural numbers will be
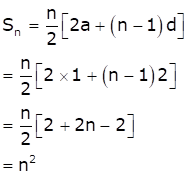
Hence, option (c) is correct.
Solution 29
Let d be the common difference of the two A.P.'s.
First term of 1st A.P. (a) = 8
First term of 2nd A.P. (a') = 3
Now, the 30th term of 1st A.P. is
a30 = a + (30 - 1)d
i.e. a30 = 8 + 29d … (i)
The 30th term of 2nd A.P. is
a'30 = a' + (30 - 1)d
a'30 = 3 + 29d … (ii)
Difference between these 30th terms is
a30 - a'30 = (8 + 29d) - (3 + 29d) = 5
Hence, option (d) is correct.
Solution 30
As 18, a, b, -3 are in A.P.
So, the difference between every two consecutive terms will be equal.
i.e. a - 18 = b - a = -3 - b
i.e. a - 18 = -3 - b
i.e. a + b = 18 - 3
i.e. a + b = 15
Hence, option (d) is correct.
Solution 31
Let Sn and S'n denotes the sum of first n terms of the two APs respectively.
![]()
Ratio of the sum of two APs is
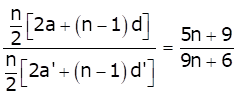
Replacing n with (2n - 1), we get
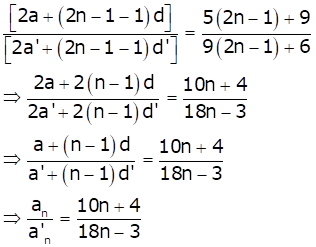
So, the ratio of their 18th terms is
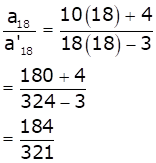
Hence, option (a) is correct.
Solution 32
![]()
Here, 5, 9, 13, … forms an A.P. with first term (a) = 5 and common difference (d) = 4
Also, 7, 9, 11, … forms an A.P. with first term (a') = 7 and common difference (d') = 2
We know that, sum of n terms of an A.P. is given by
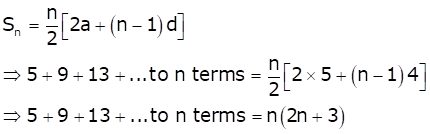
And, ![]()
![]()
From (i), we get
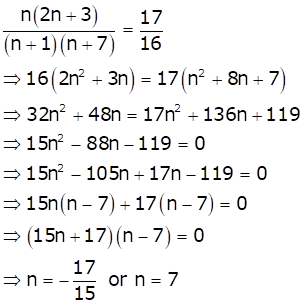
Since the number of terms can't be negative, so n = 7.
Hence, option (b) is correct.
Solution 33
Let the A.P. be a1, a2, a3, …
When Sn is the sum of n terms of an A.P., nth term will be
an = Sn - Sn-1
But, Sn = 3n2 + 5n
So, the nth term will be
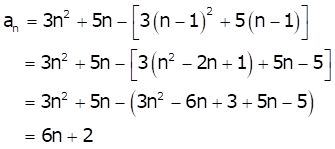
Let 164 be the nth term
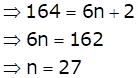
Hence, option (b) is correct.
Solution 34
The nth term of an A.P. is given as
an = 2n + 1
∴ First term = a1 = 2(1) + 1 = 3
a2 = 2(2) + 1 = 5
So, the common difference (d) = a2 - a1 = 2
Now, the sum of n terms of an A.P. is given by
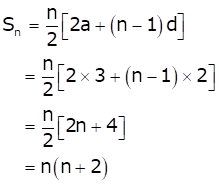
Hence, option (b) is correct.
Solution 35
The nth term of an A.P. is given by
an = a + (n - 1)d
Ratio of 18th and 11th terms is
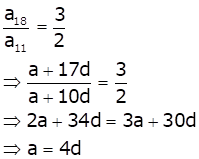
Now, the ratio of 21st and 5th terms is
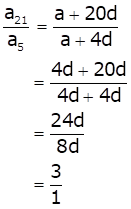
Hence, option (b) is correct.
Solution 36
The n odd natural numbers are 1, 3, 5, … n.
These terms forms an A.P. with first term (a) = 1 and common difference (d) = 2.
So, the sum of first n odd natural numbers will be
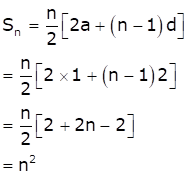
Now, the sum of first 20 odd natural numbers is
![]()
Hence, option (c) is correct.
Solution 37
The common difference of an A.P. with terms a1, a2, a3, … is given by
d = a2 - a1 = a3 - a2 = a4 - a3 = …
In the A.P. ![]() we have
we have
![]()
Therefore, ![]()
Hence, option (a) is correct.
Solution 38
The common difference of an A.P. with terms a1, a2, a3, … is given by
d = a2 - a1 = a3 - a2 = a4 - a3 = …
In the given A.P. ![]() we have
we have
![]()
Therefore, ![]()
Hence, option (c) is correct.
Solution 39
The common difference of an A.P. with terms a1, a2, a3, … is given by
d = a2 - a1 = a3 - a2 = a4 - a3 = …
In the given A.P. ![]() we have
we have
![]()
Therefore, ![]()
Hence, option (d) is correct.
Solution 40
Given: k, 2k - 1 and 2k + 1 are three consecutive terms of an AP
Therefore, common difference (d) = (2k - 1) - k
Also, d = (2k + 1) - (2k - 1)
∴ (2k - 1) - k = (2k + 1) - (2k - 1)
∴ k - 1 = 1 + 1
∴ k = 3
Hence, option (b) is correct.
Solution 41
The given A.P. is ![]()
i.e. ![]()
Here, first term (a) ![]()
The common difference (d) = ![]()
As the A.P. is given by a, (a + d), (a + 2d), (a + 3d), …
So, the next term will be
(a + 3d) = ![]()
Hence, option (d) is correct.
Solution 42
As the terms 3y - 1, 3y + 5 and 5y + 1 are in A.P.
Therefore, we have
3y + 5 - (3y - 1) = 5y + 1 - (3y + 5)
∴ 3y + 5 - 3y + 1 = 5y + 1 - 3y - 5
∴ 6 = 2y - 4
∴ y = 5
Hence, option (c) is correct.
Solution 43
The first five multiples of 3 are 3, 6, 9, 12, 15.
These terms form an A.P. with,
First term (a) = 3 and common difference (d) = 3
We know that, sum of first n terms of an A.P. is ![]()
As sum of first 5 multiples is same as sum of first 5 terms of an A.P., we have
Sum of first five multiples = S5
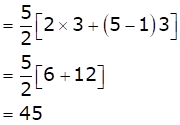
Hence, option (a) is correct.
Solution 44
For the given A.P. 10, 6, 2, …, we have
First term (a) = 10 and common difference (d) = -4
We know that, sum of first n terms of an A.P. is given by
![]()
So, the sum of first 16 terms will be

Hence, option (a) is correct.
Solution 45
In the A.P., we have
First term (a) = -5 and common difference (d) = 2
We know that, sum of first n terms of an A.P. is given by
![]()
So, the sum of first 6 terms will be
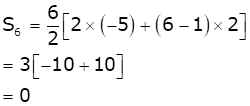
Hence, option (a) is correct.
Solution 46
In the A.P., first term (a) = -11, last term (l) = 49 and common difference (d) = 3
Here, nth term from the end = l - (n - 1)d
Therefore,
4th term from the end = 49 - (4 - 1)(3)
= 49 - 9
= 40
Hence, option (b) is correct.
Solution 47
In the given A.P., first term (a) = 21 and common difference (d) = 21
Let 210 be the nth term of the AP.
So, we have
210 = a + (n - 1)d
210 = 21 + (n - 1)(21)
21(n - 1)= 189
n - 1 = 9
Therefore, n = 10
Hence, option (b) is correct.
Solution 48
Given: 2nd term = 13 and 5th term = 25
∴ a + (2 - 1)d = 13 and a + (5 - 1)d = 25
∴ a + d = 13 … (i) and,
a + 4d = 25 … (ii)
Subtracting (i) from (ii), we have
3d = 12
Therefore, d = 4
Substituting the value of 'd' in (i), we get
a = 9
So, the 7th term will be
a7 = a + 6d = 9 + 24 = 33
Hence, option (b) is correct.
Solution 49
As 2x, x + 10 and 3x + 2 are the three consecutive terms of an A.P.
We have
x + 10 - 2x = 3x + 2 - (x + 10)
∴ 10 - x = 2x - 8
∴ 3x = 18
Thus, x = 6
Hence, option (a) is correct.
Solution 50
In the A.P., first term = p and common difference = q
The 10th term will be
a10 = p + (10 - 1)q
= p + 9q
Hence, option (c) is correct.