Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 10 - Quadrilaterals
Quadrilaterals Exercise MCQ
Solution 1
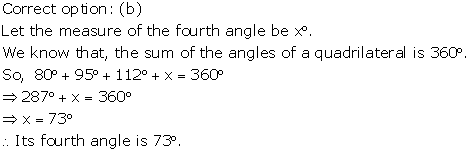
Solution 2

Solution 3

Solution 4
Correct option: (a)
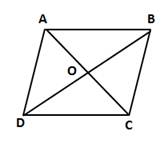
ABCD is a rhombus.
⇒ AD ∥ BC and AC is the transversal.
⇒ ∠DAC = ∠ACB (alternate angles)
⇒ ∠DAC = 50°
In ΔAOD, by angle sum property,
∠AOD + ∠DAO + ∠ADO = 180°
⇒ 90° + ∠50° + ∠ADO = 180°
⇒ ∠ADO = 40°
⇒ ∠ADB = 40°
Solution 5

Solution 6

Solution 7
![]()

Solution 8
![]()

Solution 9
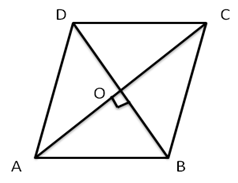
Correct option: (b)
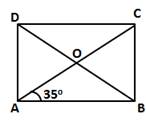
∠DAO + ∠OAB = ∠DAB
⇒ ∠DAO + 35° = 90°
⇒ ∠DAO = 55°
ABCD is a rectangle and diagonals of a rectangle are equal and bisect each other.
OA = OD
⇒ ∠ODA = ∠DAO (angles opposte to equal sides are equal)
⇒ ∠ODA = 55°
In DODA, by angle sum property,
∠ODA + ∠DAO + ∠AOD = 180°
⇒ 55° + ∠55° + ∠AOD = 180°
⇒ ∠AOD = 70°
Solution 10

Solution 11
![]()
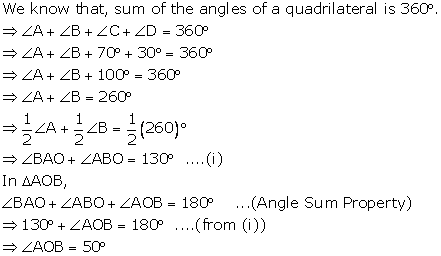
Solution 12
![]()

Solution 13
Correct option: (c)
The bisectors of the angles of a parallelogram enclose a rectangle.
Solution 14
Correct option: (d)
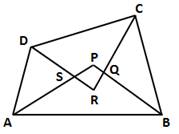
In ΔAPB, by angle sum property,
∠APB + ∠PAB + ∠PBA = 180°
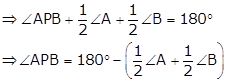
In ΔCRD, by angle sum property,
∠CRD + ∠RDC + ∠RCD = 180°

Now, ∠SPQ + ∠SRQ = ∠APB + ∠CRD
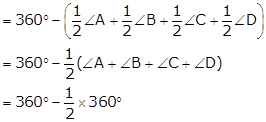
= 360° - 180°
= 180°
Now, ∠PSR + ∠PQR = 360° - (∠SPQ + ∠SRQ)
= 360° - 180°
= 180°
Hence, PQRS is a quadrilateral whose opposite angles are supplementary.
Solution 15

Solution 16
Solution 17

Solution 18

Solution 19

Solution 20
Correct option: (d)
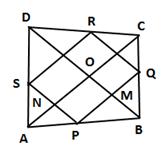
In ΔABC, P and Q are the mid-points of sides AB and BC respectively.
![]()
In ΔADC, R and S are the mid-points of sides CD and AD respectively.
![]()
From (i) and (ii),
PQ ∥ RS and PQ = RS
Thus, in quadrilateral PQRS, a pair of opposite sides are equal are parallel.
So, PQRS is a parallelogram.
Let the diagonals AC and BD intersect at O.
Now, in ΔABD, P and S are the mid-points of sides AB and AD respectively.

Thus, in quadrilateral PMON, PM ∥ NO and PN ∥ MO.
⇒ PMON is a parallelogram.
⇒ ∠MPN = ∠MON (opposite angles of a parallelogram are equal)
⇒ ∠MPN = ∠BOA (since ∠BOA = ∠MON)
⇒ ∠MPN = 90° (since AC ⊥ BD, ∠BOA = 90°)
⇒ ∠QPS = 90°
Thus, PQRS is a parallelogram whose one angle, i.e. ∠QPS = 90°.
Hence, PQRS is a rectangle if AC ⊥ BD.
Solution 21
Correct option: (c)
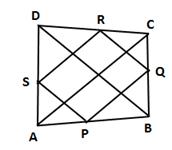
In ΔABC, P and Q are the mid-points of sides AB and BC respectively.
![]()
In ΔBCD, Q and R are the mid-points of sides BC and CD respectively.
![]()
In ΔADC, S and R are the mid-points of sides AD and CD respectively.
![]()
In ΔABD, P and S are the mid-points of sides AB and AD respectively.
![]()
⇒ PQ ∥ RS and QR ∥ SP [From (i), (ii), (iii) and (iv)]
Thus, PQRS is a parallelogram.
Now, AC = BD (given)
![]()
⇒ PQ = QR = RS = SP [From (i), (ii), (iii) and (iv)]
Hence, PQRS is a rhombus if diagonals of ABCD are equal.
Solution 22
Correct option: (d)
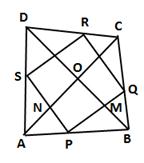
In ΔABC, P and Q are the mid-points of sides AB and BC respectively.
![]()
In ΔBCD, Q and R are the mid-points of sides BC and CD respectively.
![]()
In ΔADC, S and R are the mid-points of sides AD and CD respectively.
![]()
In ΔABD, P and S are the mid-points of sides AB and AD respectively.
![]()
⇒ PQ || RS and QR || SP [From (i), (ii), (iii) and (iv)]
Thus, PQRS is a parallelogram.
Now, AC = BD (given)
![]()
⇒ PQ = QR = RS = SP [From (i), (ii), (iii) and (iv)]
Let the diagonals AC and BD intersect at O.
Now,
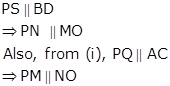
Thus, in quadrilateral PMON, PM || NO and PN || MO.
⇒ PMON is a parallelogram.
⇒ ∠MPN = ∠MON (opposite angles of a parallelogram are equal)
⇒ ∠MPN = ∠BOA (since ∠BOA = ∠MON)
⇒ ∠MPN = 90° (since AC ⊥ BD, ∠BOA = 90°)
⇒ ∠QPS = 90°
Thus, PQRS is a parallelogram such that PQ = QR = RS = SP and ∠QPS = 90°.
Hence, PQRS is a square if diagonals of ABCD are equal and perpendicular.
Solution 23
![]()

Solution 24

Solution 25

Solution 26

Solution 27
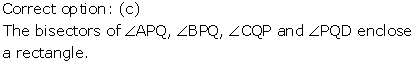
Solution 28

Solution 29

Solution 30

Solution 31
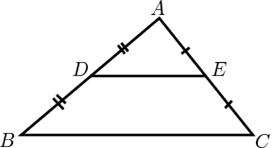
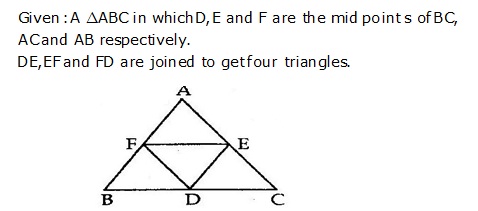
Correct option: (b)
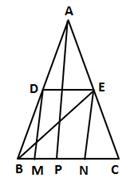
In ΔABC, D and E are the mid-points of sides AB and AC respectively.
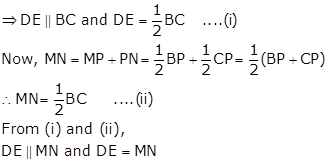
Hence, DENM is a parallelogram.
Solution 32
![]()


Solution 33
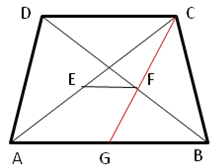

Solution 34

Solution 35

Solution 36
![]()
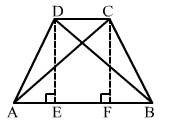

Solution 37

Solution 38
![]()
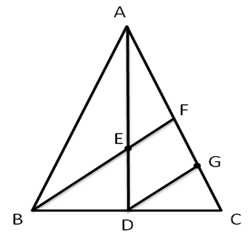

Solution 39

Solution 40

Solution 41

Solution 42
Since opposite angles of quadrilateral are equal, PQRS is a parallelogram.
⇒ PQ = SR (opposite sides of parallelogram are equal)
⇒ PQ = 2 cm
Solution 43
The given statement is false.
Diagonals of a parallelogram bisect each other.
Solution 44
In quadrilateral PQRS, ∠P and ∠S are adjacent angles.
Since the sum of adjacent angles ≠ 180°, PQRS is not a parallelogram.
Hence, PQRS is a trapezium.
Solution 45
The given statement is false.
We know that the sum of all the four angles of a quadrilateral is 360°.
If all the angles of a quadrilateral are acute, the sum will be less than 360°.
Solution 46
The given statement is true.
We know that the sum of all the four angles of a quadrilateral is 360°.
If all the angles of a quadrilateral are right angles,
Sum of all angles of a quadrilateral = 4 × 90° = 360°
Solution 47
The given statement is false.
We know that the sum of all the four angles of a quadrilateral is 360°.
If all the angles of a quadrilateral are obtuse, the sum will be more than 360°.
Solution 48
We know that the sum of all the four angles of a quadrilateral is 360°.
Here,
70° + 115° + 60° + 120° = 365° ≠ 360°
Hence, we cannot form a quadrilateral with given angles.
Solution 49
A quadrilateral whose all angles are equal is a rectangle.
Solution 50
D and E are respectively the midpoints of the sides AB and BC of ΔABC.
Thus, by mid-point theorem, we have
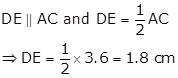
Solution 51
Since the diagonals PR and QS of quadrilateral PQRS bisect each, PQRS is a parallelogram.
Now, adjacent angles of parallelogram are supplementary.
⇒ ∠Q + ∠R = 180°
⇒ 56° + ∠R = 180°
⇒ ∠R = 124°
Solution 52
AFDE is a parallelogram
⇒ AF = ED …(i)
BDEF is a parallelogram.
⇒ FB = ED …(ii)
From (i) and (ii),
AF = FB
Solution 53
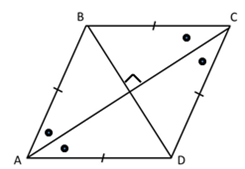
Correct option: (a)
If the diagonals of a quad. ABCD bisect each other, then the quad. ABCD is a parallelogram.
So, I gives the answer.
If the diagonals are equal, then the quad. ABCD is a parallelogram.
So, II gives the answer.
Solution 54
Correct option: (c)
If the quad. ABCD is a ‖gm, it could be a rectangle or square or rhombus.
So, statement I is not sufficient to answer the question.
If the diagonals AC and BD are perpendicular to each other, then the ‖gm could be a square or rhombus.
So, statement II is not sufficient to answer the question.
However, if the statements are combined, then the quad. ABCD is a rhombus.
Solution 55
Correct option: (c)
If the diagonals of a ‖gm ABCD are equal, then ‖gm ABCD could either be a rectangle or a square.
If the diagonals of the ‖gm ABCD intersect at right angles, then the ‖gm ABCD could be a square or a rhombus.
However, if both the statements are combined, then ‖gm ABCD will be a square.
Solution 56
Correct option: (b)
If the opposite sides of a quad. ABCD are equal, the quadrilateral is a parallelogram.
If the opposite angles are equal, then the quad. ABCD is a parallelogram.
Solution 57

Solution 58
![]()
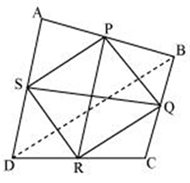

The Reason (R) is true and is the correct explanation for the Assertion (A).
Solution 59
![]()

Solution 60

Solution 61

Solution 62

Solution 63
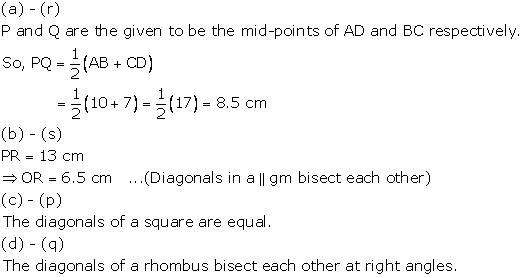
Quadrilaterals Exercise Ex. 10B
Solution 1
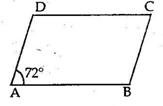
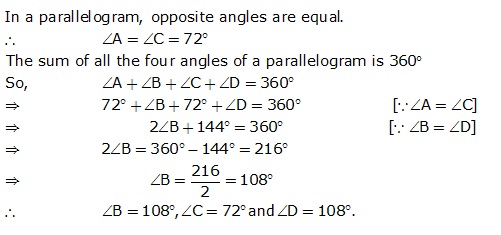
Solution 2
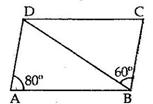

Solution 3
ABCD is a parallelogram.
Hence, AD || BC.
⇒ ∠DAM = ∠AMB (alternate angles)
⇒ ∠BAM = ∠AMB (since ∠BAM = ∠DAM)
⇒ BM = AB (sides opposite to equal angles are equal)
But, AB = CD (opposite sides of a parallelogram)
⇒ BM = AB = CD ….(i)
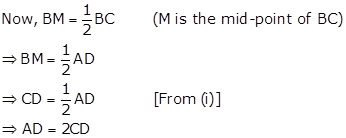
Solution 4
![]()
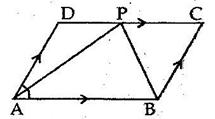


Solution 5
![]()
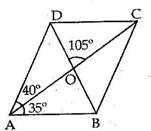

Solution 6
Solution 7
Solution 8
Solution 9

Solution 10
![]()
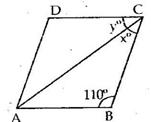
![]()

![]()

Solution 11
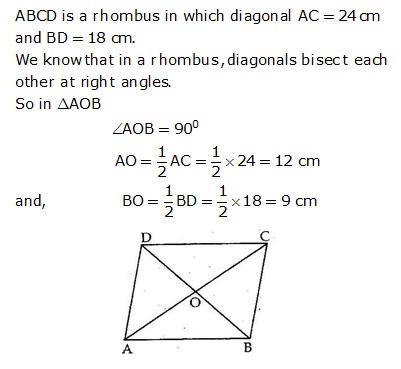

Solution 12

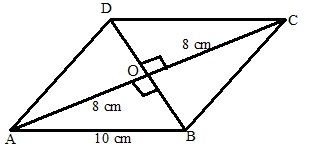

Solution 13
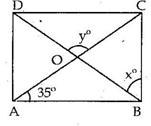


Solution 14
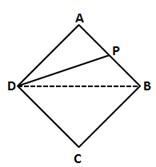
Let the altitude from D to the side AB bisect AB at point P.
Join BD.
In ΔAMD and ΔBMD,
AM = BM (M is the mid-point of AB)
∠AMD = ∠BMD (Each 90°)
MD = MD (common)
∴ ΔAMD ≅ ΔBMD (by SAS congruence criterion)
⇒ AD = BD (c.p.c.t.)
But, AD = AB (sides of a rhombus)
⇒ AD = AB = BD
⇒ ΔADB is an equilateral triangle.
⇒ ∠A = 60°
⇒ ∠C = ∠A = 60° (opposite angles are equal)
⇒ ∠B = 180° - ∠A = 180° - 60° = 120°
⇒ ∠D = ∠B = 120°
Hence, in rhombus ABCD, ∠A = 60°, ∠B = 120°, ∠C = 60° and ∠D = 120°.
Solution 15
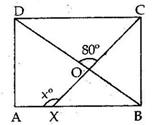

Solution 16
In ΔABC and ΔADC,
AB = AD (sides of a rhombus are equal)
BC = CD (sides of a rhombus are equal)
AC = AC (common)
∴ ΔABC ≅ ΔADC (by SSS congruence criterion)
⇒ ∠BAC = ∠DAC and ∠BCA = ∠DCA (c.p.c.t.)
⇒ AC bisects ∠A as well as ∠C.
Similarly,
In ΔBAD and ΔBCD,
AB = BC (sides of a rhombus are equal)
AD = CD (sides of a rhombus are equal)
BD = BD (common)
∴ ΔBAD ≅ ΔBCD (by SSS congruence criterion)
⇒ ∠ABD = ∠CBD and ∠ADB = ∠CDB (c.p.c.t.)
⇒ BD bisects ∠B as well as ∠D.
Solution 17
In ΔAMO and ΔCNO
∠MAO = ∠NCO (AB ∥ CD, alternate angles)
AM = CN (given)
∠AOM = ∠CON (vertically opposite angles)
∴ ΔAMO ≅ ΔCNO (by ASA congruence criterion)
⇒ AO = CO and MO = NO (c.p.c.t.)
⇒ AC and MN bisect each other.
Solution 18
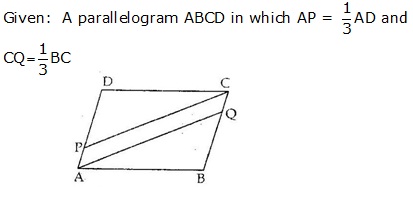

Solution 19

Solution 20
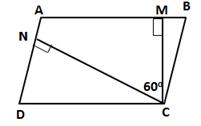
∠DCM = ∠DCN + ∠MCN
⇒ 90° = ∠DCN + 60°
⇒ ∠DCN = 30°
In ΔDCN,
∠DNC + ∠DCN + ∠D = 180°
⇒ 90° + 30° + ∠D = 180°
⇒ ∠D = 60°
⇒ ∠B = ∠D = 60° (opposite angles of parallelogram are equal)
⇒ ∠A = 180° - ∠B = 180° - 60° = 120°
⇒ ∠C = ∠A = 120°
Thus, the angles of a parallelogram are 60°, 120°, 60° and 120°.
Solution 21
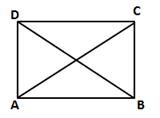
(i) ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C.
⇒ ∠BAC = ∠DAC ….(i)
And ∠BCA = ∠DCA ….(ii)
Since every rectangle is a parallelogram, therefore
AB ∥ DC and AC is the transversal.
⇒ ∠BAC = ∠DCA (alternate angles)
⇒ ∠DAC = ∠DCA [From (i)]
Thus, in ΔADC,
AD = CD (opposite sides of equal angles are equal)
But, AD = BC and CD = AB (ABCD is a rectangle)
⇒ AB = BC = CD = AD
Hence, ABCD is a square.
(ii) In ΔBAD and ΔBCD,
AB = CD
AD = BC
BD = BD
∴ ΔBAD ≅ ΔBCD (by SSS congruence criterion)
⇒ ∠ABD = ∠CBD and ∠ADB = ∠CDB (c.p.c.t.)
Hence, diagonal BD bisects ∠B as well as ∠D.
Solution 22

Solution 23

Solution 24
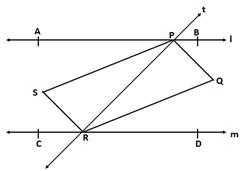
l ∥ m and t is a transversal.
⇒ ∠APR = ∠PRD (alternate angles)
![]()
⇒ ∠SPR = ∠PRQ (PS and RQ are the bisectors of ∠APR and ∠PRD)
Thus, PR intersects PS and RQ at P and R respectively such that ∠SPR = ∠PRQ i.e., alternate angles are equal.
⇒ PS ∥ RQ
Similarly, we have SR ∥ PQ.
Hence, PQRS is a parallelogram.
Now, ∠BPR + ∠PRD = 180° (interior angles are supplementary)
⇒ 2∠QPR + 2∠QRP = 180° (PQ and RQ are the bisectors of ∠BPR and ∠PRD)
⇒ ∠QPR + ∠QRP = 90°
In ΔPQR, by angle sum property,
∠PQR + ∠QPR + ∠QRP = 180°
⇒ ∠PQR + 90° = 180°
⇒ ∠PQR = 90°
Since PQRS is a parallelogram,
∠PQR = ∠PSR
⇒ ∠PSR = 90°
Now, ∠SPQ + ∠PQR = 180° (adjacent angles in a parallelogram are supplementary)
⇒ ∠SPQ + 90° = 180°
⇒ ∠SPQ = 90°
⇒ ∠SRQ = 90°
Thus, all the interior angles of quadrilateral PQRS are right angles.
Hence, PQRS is a rectangle.
Solution 25
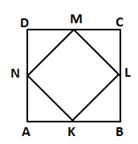
AK = BL = CM = DN (given)
⇒ BK = CL = DM = AN (i)(since ABCD is a square)
In ΔAKN and ΔBLK,
AK = BL (given)
∠A = ∠B (Each 90°)
AN = BK [From (i)]
∴ ΔAKN ≅ ΔBLK (by SAS congruence criterion)
⇒ ∠AKN = ∠BLK and ∠ANK = ∠BKL (c.p.c.t.)
But, ∠AKN + ∠ANK = 90° and ∠BLK + ∠BKL = 90°
⇒ ∠AKN + ∠ANK + ∠BLK + ∠BKL = 90° + 90°
⇒ 2∠AKN + 2∠BKL = 180°
⇒ ∠AKN + ∠BKL = 90°
⇒ ∠NKL = 90°
Similarly, we have
∠KLM = ∠LMN = ∠MNK = 90°
Hence, KLMN is a square.
Solution 26
![]()


Solution 27

Quadrilaterals Exercise Ex. 10A
Solution 1
Let the measure of the fourth angle = x°
For a quadrilateral, sum of four angles = 360°
⇒ x° + 75° + 90° + 75° = 360°
⇒ x° = 360° - 240°
⇒ x° = 120°
Hence, the measure of fourth angle is 120°.
Solution 2

Solution 3
Since AB || DC
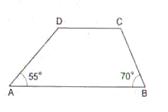

Solution 4
Given:![]()



Solution 5
![]()
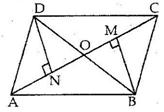

Solution 6
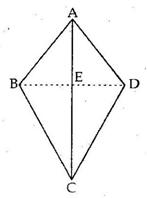


Solution 7
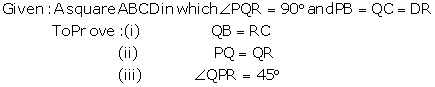
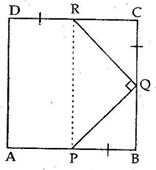

Solution 8
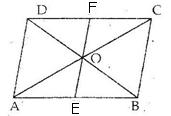
Given: O is a point within a quadrilateral ABCD


Solution 9
Given: ABCD is a quadrilateral and AC is one of its diagonals.
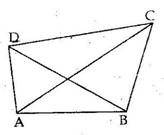

Solution 10
Given: ABCD is a quadrilateral.
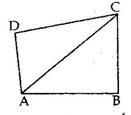
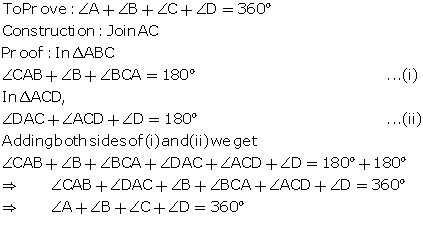
Quadrilaterals Exercise Ex. 10C
Solution 1
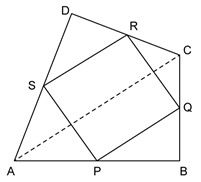
(i) In ΔABC, P and Q are the mid-points of sides AB and BC respectively.
![]()
(ii) In ΔADC, R and S are the mid-points of sides CD and AD respectively.
![]()
From (i) and (ii), we have
PQ = SR and PQ ∥ SR
(iii) Thus, in quadrilateral PQRS, one pair of opposite sides are equal and parallel.
Hence, PQRS is a parallelogram.
Solution 2

Let ΔABC be an isosceles right triangle, right-angled at B.
⇒ AB = BC
Let PBSR be a square inscribed in ΔABC with common ∠B.
⇒ PB = BS = SR = RP
Now, AB - PB = BC - BS
⇒ AP = CS ….(i)
In ΔAPR and ΔCSR
AP = CS [From (i)
∠APR = ∠CSR (Each 90°)
PR = SR (sides of a square)
∴ ΔAPR ≅ ΔCSR (by SAS congruence criterion)
⇒ AR = CR (c.p.c.t.)
Thus, point R bisects the hypotenuse AC.
Solution 3
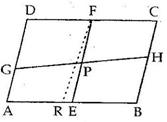

Solution 4
In ΔAOM and ΔCON
∠MAO = ∠OCN (Alternate angles)
AO = OC (Diagonals of a parallelogram bisect each other)
∠AOM = ∠CON (Vertically opposite angles)
∴ ΔAOM ≅ ΔCON (by ASA congruence criterion)
⇒ MO = NO (c.p.c.t.)
Thus, MN is bisected at point O.
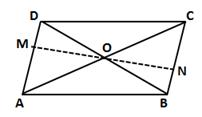
Solution 5
Construction: Join diagonal QS. Let QS intersect MN at point O.

PQ ∥ SR and MN ∥ PQ
⇒ PQ ∥ MN ∥ SR
By converse of mid-point theorem a line drawn, through the mid-point of any side of a triangle and parallel to another side bisects the third side.
Now, in ΔSPQ
MO ∥ PQ and M is the mid-point of SP
So, this line will intersect QS at point O and O will be the mid-point of QS.
Also, MN ∥ SR
Thus, in ΔQRS, ON ∥ SR and O is the midpoint of line QS.
So, by using converse of mid-point theorem, N is the mid-point of QR.
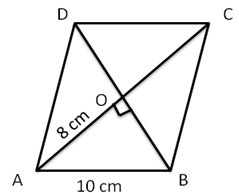
Solution 6
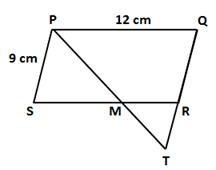
PM is the bisector of ∠P.
⇒ ∠QPM = ∠SPM ….(i)
PQRS is a parallelogram.
∴ PQ ∥ SR and PM is the transversal.
⇒ ∠QPM = ∠MS (ii)(alternate angles)
From (i) and (ii),
∠SPM = ∠PMS ….(iii)
⇒ MS = PS = 9 cm (sides opposite to equal angles are equal)
Now, ∠RMT = ∠PMS (iv)(vertically opposite angles)
Also, PS ∥ QT and PT is the transversal.
∠RTM = ∠SPM
⇒ ∠RTM = ∠RMT
⇒ RT = RM (sides opposite to equal angles are equal)
RM = SR - MS = 12 - 9 = 3 cm
⇒ RT = 3 cm
Solution 7

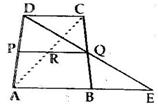

Solution 8
![]()
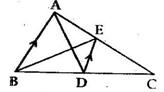

Solution 9
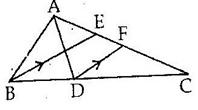
Solution 10

Solution 11
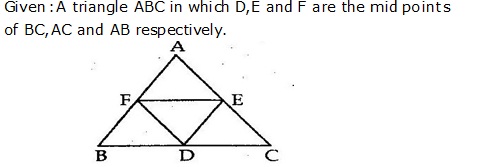

Solution 12
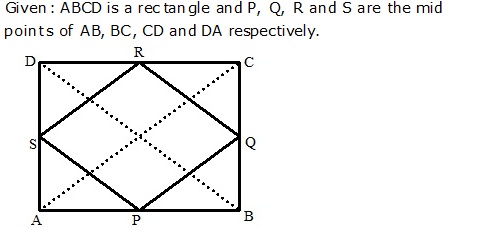

Solution 13
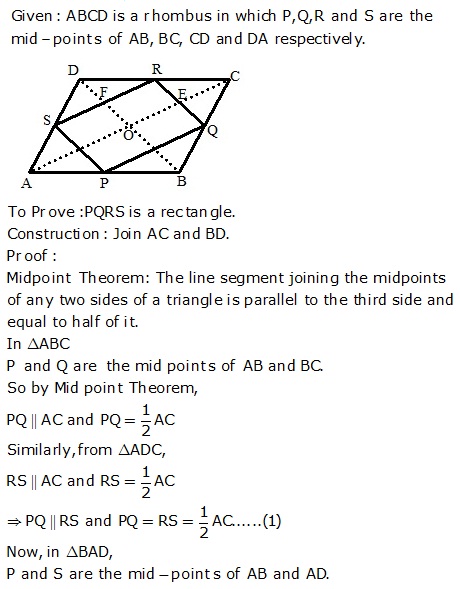

Solution 14
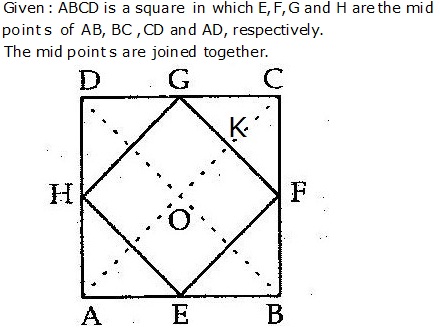



Solution 15
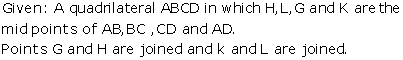
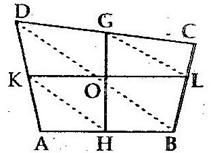

Solution 16
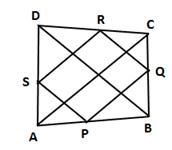
In ΔABC, P and Q are the mid-points of sides AB and BC respectively.
![]()
In ΔBCD, Q and R are the mid-points of sides BC and CD respectively.
![]()
In ΔADC, S and R are the mid-points of sides AD and CD respectively.
![]()
In ΔABD, P and S are the mid-points of sides AB and AD respectively.
![]()
⇒ PQ || RS and QR || SP [From (i), (ii), (iii) and (iv)]
Thus, PQRS is a parallelogram.
Now, AC = BD (given)
![]()
⇒ PQ = QR = RS = SP [From (i), (ii), (iii) and (iv)]
Hence, PQRS is a rhombus.
Solution 17
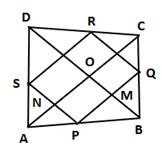
In ΔABC, P and Q are the mid-points of sides AB and BC respectively.
![]()
In ΔADC, R and S are the mid-points of sides CD and AD respectively.
![]()
From (i) and (ii),
PQ || RS and PQ = RS
Thus, in quadrilateral PQRS, a pair of opposite sides are equal are parallel.
So, PQRS is a parallelogram.
Let the diagonals AC and BD intersect at O.
Now, in ΔABD, P and S are the mid-points of sides AB and AD respectively.
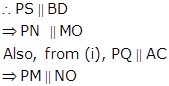
Thus, in quadrilateral PMON, PM || NO and PN || MO.
⇒ PMON is a parallelogram.
⇒ ∠MPN = ∠MON (opposite angles of a parallelogram are equal)
⇒ ∠MPN = ∠BOA (since ∠BOA = ∠MON)
⇒ ∠MPN = 90° (since AC ⊥ BD, ∠BOA = 90°)
⇒ ∠QPS = 90°
Thus, PQRS is a parallelogram whose one angle, i.e. ∠QPS = 90°.
Hence, PQRS is a rectangle.
Solution 18
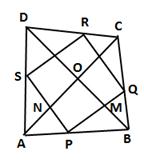
In ΔABC, P and Q are the mid-points of sides AB and BC respectively.
![]()
In ΔBCD, Q and R are the mid-points of sides BC and CD respectively.
![]()
In ΔADC, S and R are the mid-points of sides AD and CD respectively.
![]()
In ΔABD, P and S are the mid-points of sides AB and AD respectively.
![]()
⇒ PQ || RS and QR || SP [From (i), (ii), (iii) and (iv)]
Thus, PQRS is a parallelogram.
Now, AC = BD (given)
![]()
⇒ PQ = QR = RS = SP [From (i), (ii), (iii) and (iv)]
Let the diagonals AC and BD intersect at O.
Now,
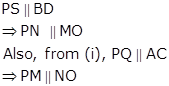
Thus, in quadrilateral PMON, PM || NO and PN || MO.
⇒ PMON is a parallelogram.
⇒ ∠MPN = ∠MON (opposite angles of a parallelogram are equal)
⇒ ∠MPN = ∠BOA (since ∠BOA = ∠MON)
⇒ ∠MPN = 90° (since AC ⊥ BD, ∠BOA = 90°)
⇒ ∠QPS = 90°
Thus, PQRS is a parallelogram such that PQ = QR = RS = SP and ∠QPS = 90°.
Hence, PQRS is a square.


