Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 7 - Lines And Angles
Lines And Angles Exercise MCQ
Solution 1
Correct option: (d)
In a right triangle, one angle is 90° and the sum of acute angles of a right triangle is 90°.
Solution 2
Correct option: (b)
Let each interior opposite angle be x.
Then, x + x = 110° (Exterior angle property of a triangle)
⇒ 2x = 110°
⇒ x = 55°
Solution 3

Solution 4
Correct option: (d)
Let ∠A = 130°
In ΔABC, by angle sum property,
∠B + ∠C + ∠A = 180°
⇒ ∠B + ∠C + 130° = 180°
⇒ ∠B + ∠C = 50°
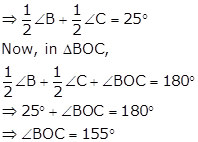
Solution 5
Correct option: (b)
AOB is a straight line.
⇒ ∠AOB = 180°
⇒ 60° + 5x° + 3x° = 180°
⇒ 60° + 8x° = 180°
⇒ 8x° = 120°
⇒ x = 15°
Solution 6
Correct option: (c)
By angle sum property,
2x + 3x + 4x = 180°
⇒ 9x = 180°
⇒ x = 20°
Hence, largest angle = 4x = 4(20°) = 80°
Solution 7
Correct option: (c)
Through B draw YBZ ∥ OA ∥ CD.

Now, OA ∥ YB and AB is the transversal.
⇒ ∠OAB + ∠YBA = 180° (interior angles are supplementary)
⇒ 110° + ∠YBA = 180°
⇒ ∠YBA = 70°
Also, CD ∥ BZ and BC is the transversal.
⇒ ∠DCB + ∠CBZ = 180° (interior angles are supplementary)
⇒ 130° + ∠CBZ = 180°
⇒ ∠CBZ = 50°
Now, ∠YBZ = 180° (straight angle)
⇒ ∠YBA + ∠ABC + ∠CBZ = 180°
⇒ 70° + x + 50° = 180°
⇒ x = 60°
⇒ ∠ABC = 60°
Solution 8
Correct option: (a)
Two angles are said to be complementary, if the sum of their measures is 90°.
Clearly, the measures of each of the angles have to be less than 90°.
Hence, each angle is an acute angle.
Solution 9
Correct option: (d)
An angle which measures more than 180o but less than 360o is called a reflex angle.
Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15
Correct option: (a)
Option (a) is false, since through a given point we can draw an infinite number of straight lines.
Solution 16

Solution 17

Solution 18

Solution 19

Solution 20

Solution 21
Correct option: (c)
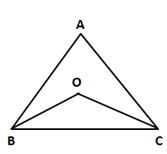
Let ∠AOC = x°
Draw YOZ ∥ CD ∥ AB.
Now, YO ∥ AB and OA is the transversal.
⇒ ∠YOA = ∠OAB = 60° (alternate angles)
Again, OZ ∥ CD and OC is the transversal.
⇒ ∠COZ + ∠OCD = 180° (interior angles)
⇒ ∠COZ + 110° = 180°
⇒ ∠COZ = 70°
Now, ∠YOZ = 180° (straight angle)
⇒ ∠YOA + ∠AOC + ∠COZ = 180°
⇒ 60° + x + 70° = 180°
⇒ x = 50°
⇒ ∠AOC = 50°
Solution 22


Solution 23

Solution 24

Solution 25
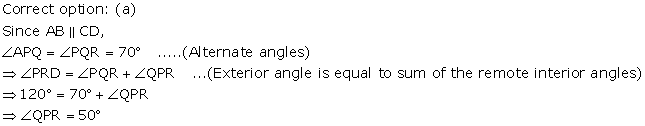
Solution 26

Solution 27

Solution 28
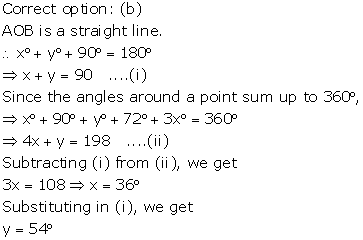
Lines And Angles Exercise Ex. 7A
Solution 1
(i) Angle: Two rays having a common end point form an angle.
(ii) Interior of an angle: The interior of ![]() AOB is the set of all points in its plane, which lie on the same side of OA as B and also on same side of OB as A.
AOB is the set of all points in its plane, which lie on the same side of OA as B and also on same side of OB as A.
(iii) Obtuse angle: An angle whose measure is more than 90o but less than 180o, is called an obtuse angle.
(iv) Reflex angle: An angle whose measure is more than 180o but less than 360o is called a reflex angle.
(v) Complementary angles: Two angles are said to be complementary, if the sum of their measures is 90o.
(vi) Supplementary angles: Two angles are said to be supplementary, if the sum of their measures is 180o.
Solution 2(ii)
Complement of 16o = 90 - 16o = 74o
Solution 2(iv)
![]()

Complement of 46o 30' = 90o - 46o 30' = 43o 30'
Solution 2(i)
Complement of 55° = 90° - 55° = 35°
Solution 2(iii)
Complement of 90° = 90° - 90° = 0°
Solution 3(iv)
![]()

Supplement of 75o 36' = 180o - 75o 36' = 104o 24'
Solution 3(i)
Supplement of 42° = 180° - 42° = 138°
Solution 3(ii)
Supplement of 90° = 180° - 90° = 90°
Solution 3(iii)
Supplement of 124° = 180° - 124° = 56°
Solution 4
(i) Let the required angle be xo
Then, its complement = 90o - xo
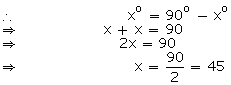
![]() The measure of an angle which is equal to
its complement is 45o.
The measure of an angle which is equal to
its complement is 45o.
(ii) Let the required angle be xo
Then, its supplement = 180o - xo
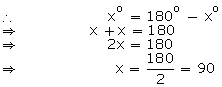
![]() The measure of an angle which is equal to
its supplement is 90o.
The measure of an angle which is equal to
its supplement is 90o.
Solution 5
Let the required angle be xo
Then its complement is 90o - xo

![]() The measure of an angle which is 36o
more than its complement is 63o.
The measure of an angle which is 36o
more than its complement is 63o.
Solution 6
Let the measure of the required angle = x°
Then, measure of its supplement = (180 - x)°
It is given that
x° = (180 - x)° - 30°
⇒ x° = 180° - x° - 30°
⇒ 2x° = 150°
⇒ x° = 75°
Hence, the measure of the required angle is 75°.
Solution 7
Let the required angle be xo
Then, its complement = 90o - xo

![]() The required angle is 72o.
The required angle is 72o.
Solution 8
Let the required angle be xo
Then, its supplement is 180o - xo

![]() The required angle is 150o.
The required angle is 150o.
Solution 9
Let the required angle be xo
Then, its complement is 90o - xo and its supplement is 180o - xo
That is we have,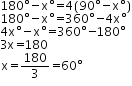
![]() The required angle is 60o.
The required angle is 60o.
Solution 10
Let the required angle be xo
Then, its complement is 90o - xo and its supplement is 180o - xo

![]() The required angle is 45o.
The required angle is 45o.
Solution 11
Let the two required angles be xo and 90o - xo.
Then ![]()
![]() 5x = 4(90 - x)
5x = 4(90 - x)
![]() 5x = 360 - 4x
5x = 360 - 4x
![]() 5x + 4x = 360
5x + 4x = 360
![]() 9x = 360
9x = 360
![]()
![]()
Thus, the required angles are 40o and 90o - xo = 90 o - 40o = 50o.
Solution 12
(2x - 5)° and (x - 10)° are complementary angles.
∴ (2x - 5)° + (x - 10)° = 90°
⇒ 2x - 5° + x - 10° = 90°
⇒ 3x - 15° = 90°
⇒ 3x = 105°
⇒ x = 35°
Lines And Angles Exercise Ex. 7B
Solution 1
Since ![]() BOC and
BOC and ![]() COA form a linear pair of angles, we have
COA form a linear pair of angles, we have
![]() BOC +
BOC + ![]() COA = 180o
COA = 180o
![]() xo + 62o = 180o
xo + 62o = 180o
![]() x = 180 - 62
x = 180 - 62
![]() x = 118o
x = 118o
Solution 2
∠AOB is a straight angle.
⇒ ∠AOB = 180°
⇒ ∠AOC + ∠COD + ∠BOD = 180°
⇒ (3x - 7)° + 55° + (x + 20)° = 180°
⇒ 4x + 68° = 180°
⇒ 4x = 112°
⇒ x = 28°
Thus, ∠AOC = (3x - 7)° = 3(28°) - 7° = 84° - 7° = 77°
And, ∠BOD = (x + 20)° = 28° + 20° = 48°
Solution 3
Since ![]() BOD and
BOD and ![]() DOA from a linear pair of angles.
DOA from a linear pair of angles.
![]()
![]() BOD +
BOD + ![]() DOA = 180o
DOA = 180o
![]()
![]() BOD +
BOD + ![]() DOC +
DOC + ![]() COA = 180o
COA = 180o
![]() xo + (2x - 19)o + (3x + 7)o = 180o
xo + (2x - 19)o + (3x + 7)o = 180o
![]() 6x - 12 = 180
6x - 12 = 180
![]() 6x = 180 + 12 = 192
6x = 180 + 12 = 192
![]()
![]()
![]() x = 32
x = 32
![]()
![]() AOC = (3x + 7)o = (3
AOC = (3x + 7)o = (3 ![]() 32 + 7)o = 103o
32 + 7)o = 103o
![]()
![]() COD = (2x - 19)o = (2
COD = (2x - 19)o = (2 ![]() 32 - 19)o = 45o
32 - 19)o = 45o
and ![]() BOD = xo = 32o
BOD = xo = 32o
Solution 4
x: y: z = 5: 4: 6
The sum of their ratios = 5 + 4 + 6 = 15
But x + y + z = 180o
[Since, XOY is a straight line]
So, if the total sum of the measures is 15, then the measure of x is 5.
If the sum of angles is 180o, then, measure of ![]()
And, if the total sum of the measures is 15, then the measure of y is 4.
If the sum of the angles is 180o, then, measure of ![]()
And ![]() z = 180o -
z = 180o - ![]() x -
x - ![]() y
y
= 180o - 60o - 48o
= 180o - 108o = 72o
![]() x = 60, y = 48 and z = 72.
x = 60, y = 48 and z = 72.
Solution 5
AOB will be a straight line, if two adjacent angles form a linear pair.
![]()
![]() BOC
+
BOC
+ ![]() AOC = 180o
AOC = 180o
![]() (4x - 36)o + (3x + 20)o
= 180o
(4x - 36)o + (3x + 20)o
= 180o
![]() 4x - 36 + 3x + 20 = 180
4x - 36 + 3x + 20 = 180
![]() 7x - 16 = 180o
7x - 16 = 180o
![]() 7x = 180 + 16 = 196
7x = 180 + 16 = 196
![]()
![]()
![]() The value of x = 28.
The value of x = 28.
Solution 6
Since
![]() AOC and
AOC and ![]() AOD form a linear pair.
AOD form a linear pair.
![]()
![]() AOC
+
AOC
+ ![]() AOD = 180o
AOD = 180o
![]() 50o +
50o + ![]() AOD = 180o
AOD = 180o
![]()
![]() AOD = 180o - 50o = 130o
AOD = 180o - 50o = 130o
![]() AOD
and
AOD
and ![]() BOC are vertically opposite angles.
BOC are vertically opposite angles.
![]()
![]() AOD =
AOD = ![]() BOC
BOC
![]()
![]() BOC = 130o
BOC = 130o
![]() BOD
and
BOD
and ![]() AOC are vertically opposite angles.
AOC are vertically opposite angles.
![]()
![]() BOD
=
BOD
= ![]() AOC
AOC
![]()
![]() BOD = 50o
BOD = 50o
Solution 7
Since ![]() COE and
COE and ![]() DOF are vertically opposite angles, we have,
DOF are vertically opposite angles, we have,
![]() COE =
COE = ![]() DOF
DOF
![]()
![]() z = 50o
z = 50o
Also ![]() BOD and
BOD and ![]() COA are vertically opposite angles.
COA are vertically opposite angles.
So, ![]() BOD =
BOD = ![]() COA
COA
![]()
![]() t = 90o
t = 90o
As ![]() COA and
COA and ![]() AOD form a linear pair,
AOD form a linear pair,
![]() COA +
COA + ![]() AOD = 180o
AOD = 180o
![]()
![]() COA +
COA + ![]() AOF +
AOF + ![]() FOD = 180o [
FOD = 180o [![]()
![]() t = 90o]
t = 90o]
![]() t + x + 50o = 180o
t + x + 50o = 180o
![]() 90o + xo + 50o = 180o
90o + xo + 50o = 180o
![]() x + 140 = 180
x + 140 = 180
![]() x = 180 - 140 = 40
x = 180 - 140 = 40
Since ![]() EOB and
EOB and ![]() AOF are vertically opposite angles
AOF are vertically opposite angles
So, ![]() EOB =
EOB = ![]() AOF
AOF
![]() y = x = 40
y = x = 40
Thus, x = 40 = y = 40, z = 50 and t = 90
Solution 8
Since
![]() COE and
COE and ![]() EOD form a linear pair of angles.
EOD form a linear pair of angles.
![]()
![]() COE +
COE + ![]() EOD = 180o
EOD = 180o
![]()
![]() COE +
COE + ![]() EOA +
EOA + ![]() AOD = 180o
AOD = 180o
![]() 5x +
5x + ![]() EOA + 2x = 180
EOA + 2x = 180
![]() 5x +
5x + ![]() BOF + 2x = 180
BOF + 2x = 180
[![]()
![]() EOA and
EOA and ![]() BOF are vertically opposite angles so,
BOF are vertically opposite angles so, ![]() EOA =
EOA = ![]() BOF]
BOF]
![]() 5x + 3x + 2x = 180
5x + 3x + 2x = 180
![]() 10x = 180
10x = 180
![]() x = 18
x = 18
Now ![]() AOD = 2xo = 2
AOD = 2xo = 2 ![]() 18o
= 36o
18o
= 36o
![]() COE = 5xo = 5
COE = 5xo = 5 ![]() 18o
= 90o
18o
= 90o
and, ![]() EOA =
EOA = ![]() BOF = 3xo = 3
BOF = 3xo = 3 ![]() 18o
= 54o
18o
= 54o
Solution 9
Let the two adjacent angles be 5x and 4x.
Now, since these angles form a linear pair.
So, 5x + 4x = 180o
![]() 9x = 180o
9x = 180o
![]()
![]()
![]() The required angles are 5x = 5x = 5
The required angles are 5x = 5x = 5 ![]() 20o
= 100o
20o
= 100o
and 4x = 4 ![]() 20o
= 80o
20o
= 80o
Solution 10
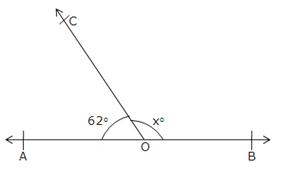
Let
two straight lines AB and CD intersect at O and let ![]() AOC = 90o.
AOC = 90o.
Now, ![]() AOC =
AOC = ![]() BOD
[Vertically opposite angles]
BOD
[Vertically opposite angles]
![]()
![]() BOD = 90o
BOD = 90o
Also,
as ![]() AOC and
AOC and ![]() AOD form a linear pair.
AOD form a linear pair.
![]() 90o +
90o + ![]() AOD = 180o
AOD = 180o
![]()
![]() AOD = 180o - 90o = 90o
AOD = 180o - 90o = 90o
Since, ![]() BOC =
BOC = ![]() AOD
[Verticallty opposite angles]
AOD
[Verticallty opposite angles]
![]()
![]() BOC = 90o
BOC = 90o
Thus, each of the remaining angles is 90o.
Solution 11
Since,
![]() AOD and
AOD and ![]() BOC are vertically opposite angles.
BOC are vertically opposite angles.
![]()
![]() AOD
=
AOD
= ![]() BOC
BOC
Now,
![]() AOD +
AOD + ![]() BOC = 280o [Given]
BOC = 280o [Given]
![]()
![]() AOD +
AOD + ![]() AOD = 280o
AOD = 280o
![]() 2
2![]() AOD = 280o
AOD = 280o
![]()
![]() AOD =
AOD = ![]()
![]()
![]() BOC =
BOC = ![]() AOD = 140o
AOD = 140o
As,
![]() AOC and
AOC and ![]() AOD form a linear pair.
AOD form a linear pair.
So, ![]() AOC +
AOC + ![]() AOD = 180o
AOD = 180o
![]()
![]() AOC + 140o = 180o
AOC + 140o = 180o
![]()
![]() AOC = 180o - 140o = 40o
AOC = 180o - 140o = 40o
Since,
![]() AOC and
AOC and ![]() BOD are vertically opposite angles.
BOD are vertically opposite angles.
![]()
![]() AOC
=
AOC
= ![]() BOD
BOD
![]()
![]() BOD = 40o
BOD = 40o
![]()
![]() BOC = 140o,
BOC = 140o, ![]() AOC = 40o ,
AOC = 40o , ![]() AOD = 140o and
AOD = 140o and ![]() BOD = 40o.
BOD = 40o.
Solution 12
Let ∠AOC = 5x and ∠AOD = 7x
Now, ∠AOC + ∠AOD = 180° (linear pair of angles)
⇒ 5x + 7x = 180°
⇒ 12x = 180°
⇒ x = 15°
⇒ ∠AOC = 5x = 5(15°) = 75° and ∠AOD = 7x = 7(15°) = 105°
Now, ∠AOC = ∠BOD (vertically opposite angles)
⇒ ∠BOD = 75°
Also, ∠AOD = ∠BOC (vertically opposite angles)
⇒ ∠BOC = 105°
Solution 13
∠BOD = 40°
⇒ AOC = ∠BOD = 40° (vertically opposite angles)
∠AOE = 35°
⇒ ∠BOF = ∠AOE = 35° (vertically opposite angles)
∠AOB is a straight angle.
⇒ ∠AOB = 180°
⇒ ∠AOE + ∠EOD + ∠BOD = 180°
⇒ 35° + ∠EOD + 40° = 180°
⇒ ∠EOD + 75° = 180°
⇒ ∠EOD = 105°
Now, ∠COF = ∠EOD = 105° (vertically opposite angles)
Solution 14
∠AOC + ∠BOC = 180° (linear pair of angles)
⇒ x + 125 = 180°
⇒ x = 55°
Now, ∠AOD = ∠BOC (vertically opposite angles)
⇒ y = 125°
Also, ∠BOD = ∠AOC (vertically opposite angles)
⇒ z = 55°
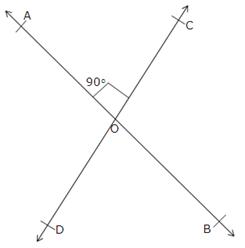
Solution 15
Given : AB and CD are two lines which are
intersecting at O. OE is a ray bisecting the ![]() BOD. OF is a ray opposite to ray OE.
BOD. OF is a ray opposite to ray OE.
To Prove: ![]() AOF
=
AOF
= ![]() COF
COF
Proof : Since ![]() are two
opposite rays,
are two
opposite rays, ![]() is a straight
line passing through O.
is a straight
line passing through O.
![]()
![]() AOF =
AOF = ![]() BOE
BOE
and ![]() COF =
COF = ![]() DOE
DOE
[Vertically opposite angles]
But ![]() BOE =
BOE = ![]() DOE (Given)
DOE (Given)
![]()
![]() AOF =
AOF = ![]() COF
COF
Hence, proved.
Solution 16
Given: ![]() is
the bisector of
is
the bisector of ![]() BCD and
BCD and ![]() is the bisector of
is the bisector of ![]() ACD.
ACD.
To Prove: ![]() ECF
= 90o
ECF
= 90o
Proof: Since ![]() ACD and
ACD and ![]() BCD forms a linear pair.
BCD forms a linear pair.
![]() ACD +
ACD + ![]() BCD = 180o
BCD = 180o
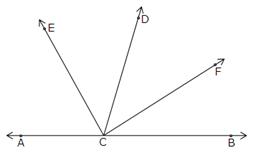
![]() ACE +
ACE + ![]() ECD +
ECD + ![]() DCF +
DCF + ![]() FCB = 180o
FCB = 180o
![]()
![]() ECD +
ECD + ![]() ECD +
ECD + ![]() DCF +
DCF + ![]() DCF = 180o
DCF = 180o
because
![]() ACE =
ACE = ![]() ECD
ECD
and ![]() DCF =
DCF = ![]() FCB
FCB
![]() 2(
2(![]() ECD) + 2 (
ECD) + 2 (![]() CDF) = 180o
CDF) = 180o
![]() 2(
2(![]() ECD +
ECD + ![]() DCF) = 180o
DCF) = 180o
![]()
![]() ECD +
ECD + ![]() DCF =
DCF = ![]()
![]()
![]() ECF = 90o (Proved)
ECF = 90o (Proved)
Lines And Angles Exercise Ex. 7C
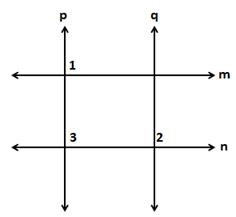
Solution 1
Given, ∠1 = 120°
Now, ∠1 + ∠2 = 180° (linear pair)
⇒ 120° + ∠2 = 180°
⇒ ∠2 = 60°
∠1 = ∠3 (vertically opposite angles)
⇒ ∠3 = 120°
Also, ∠2 = ∠4 (vertically opposite angles)
⇒ ∠4 = 60°
Line l ∥ line m and line t is a transversal.
⇒ ∠5 = ∠1 = 120° (corresponding angles)
∠6 = ∠2 = 60° (corresponding angles)
∠7 = ∠3 = 120° (corresponding angles)
∠8 = ∠4 = 60° (corresponding angles)
Solution 2
Given, ∠7 = 80°
Now, ∠7 + ∠8 = 180° (linear pair)
⇒ 80° + ∠8 = 180°
⇒ ∠8 = 100°
∠7 = ∠5 (vertically opposite angles)
⇒ ∠5 = 80°
Also, ∠6 = ∠8 (vertically opposite angles)
⇒ ∠6 = 100°
Line l ∥ line m and line t is a transversal.
⇒ ∠1 = ∠5 = 80° (corresponding angles)
∠2 = ∠6 = 100° (corresponding angles)
∠3 = ∠7 = 80° (corresponding angles)
∠4 = ∠8 = 100° (corresponding angles)
Solution 3
Given, ∠1 : ∠2 = 2 : 3
Now, ∠1 + ∠2 = 180° (linear pair)
⇒ 2x + 3x = 180°
⇒ 5x = 180°
⇒ x = 36°
⇒ ∠1 = 2x = 72° and ∠2 = 3x = 108°
∠1 = ∠3 (vertically opposite angles)
⇒ ∠3 = 72°
Also, ∠2 = ∠4 (vertically opposite angles)
⇒ ∠4 = 108°
Line l ∥ line m and line t is a transversal.
⇒ ∠5 = ∠1 = 72° (corresponding angles)
∠6 = ∠2 = 108° (corresponding angles)
∠7 = ∠3 = 72° (corresponding angles)
∠8 = ∠4 = 108° (corresponding angles)
Solution 4
Lines l and m will be parallel if 3x - 20 = 2x + 10
[Since, if corresponding angles are equal, lines are parallel]
![]() 3x - 2x = 10 + 20
3x - 2x = 10 + 20
![]() x = 30
x = 30
Solution 5
For lines l and m to be parallel to each other, the corresponding angles (3x + 5)° and (4x)° should be equal.
⇒ (3x + 5)° = 4x°
⇒ x = 5°
Solution 6
Since AB || CD and BC is a transversal.
So, ![]() BCD =
BCD = ![]() ABC = xo [Alternate angles]
ABC = xo [Alternate angles]
As BC || ED and CD is a transversal.
![]() BCD +
BCD + ![]() EDC = 180o
EDC = 180o
![]()
![]() BCD + 75o =180o
BCD + 75o =180o
![]()
![]() BCD = 180o - 75o = 105o
BCD = 180o - 75o = 105o
![]()
![]() ABC = 105o [since
ABC = 105o [since ![]() BCD =
BCD = ![]() ABC]
ABC]
![]() xo =
xo = ![]() ABC = 105o
ABC = 105o
Hence, x = 105.
Solution 7
Since AB || CD and BC is a transversal.
So, ![]() ABC =
ABC = ![]() BCD [atternate interior angles]
BCD [atternate interior angles]
![]() 70o = xo +
70o = xo + ![]() ECD(i)
ECD(i)
Now, CD || EF and CE is transversal.
So,![]() ECD +
ECD + ![]() CEF = 180o [sum of consecutive interior angles is 180o]
CEF = 180o [sum of consecutive interior angles is 180o]
![]()
![]() ECD + 130o = 180o
ECD + 130o = 180o
![]()
![]() ECD = 180o - 130o = 50o
ECD = 180o - 130o = 50o
Putting ![]() ECD = 50o in (i) we get,
ECD = 50o in (i) we get,
70o = xo + 50o
![]() x = 70 - 50 = 20
x = 70 - 50 = 20
Solution 8
AB ∥ CD and EF is transversal.
⇒ ∠AEF = ∠EFG (alternate angles)
Given, ∠AEF = 75°
⇒ ∠EFG = y = 75°
Now, ∠EFC + ∠EFG = 180° (linear pair)
⇒ x + y = 180°
⇒ x + 75° = 180°
⇒ x = 105°
∠EGD = ∠EFG + ∠FEG (Exterior angle property)
⇒ 125° = y + z
⇒ 125° = 75° + z
⇒ z = 50°
Thus, x = 105°, y = 75° and z = 50°
Solution 9(i)
Through E draw EG || CD. Now since EG||CD and ED is a transversal.
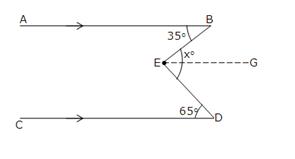
So,![]() GED =
GED = ![]() EDC = 65o[Alternate interior angles]
EDC = 65o[Alternate interior angles]
Since EG || CD and AB || CD,
EG||AB and EB is transversal.
So,![]() BEG =
BEG = ![]() ABE = 35o[Alternate interior angles]
ABE = 35o[Alternate interior angles]
So,![]() DEB = xo
DEB = xo
![]()
![]() BEG +
BEG + ![]() GED = 35o + 65o = 100o.
GED = 35o + 65o = 100o.
Hence, x = 100.
Solution 9(ii)
Through O draw OF||CD.
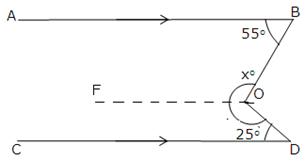
Now since OF || CD and OD is transversal.
![]() CDO +
CDO + ![]() FOD = 180o
FOD = 180o
[sum of consecutive interior angles is 180o]
![]() 25o +
25o + ![]() FOD = 180o
FOD = 180o
![]()
![]() FOD = 180o - 25o = 155o
FOD = 180o - 25o = 155o
As OF || CD and AB || CD [Given]
Thus, OF || AB and OB is a transversal.
So,![]() ABO +
ABO + ![]() FOB = 180o [sum of consecutive interior angles is 180o]
FOB = 180o [sum of consecutive interior angles is 180o]
![]() 55o +
55o + ![]() FOB = 180o
FOB = 180o
![]()
![]() FOB = 180o - 55o = 125o
FOB = 180o - 55o = 125o
Now, xo = ![]() FOB +
FOB + ![]() FOD = 125o + 155o = 280o.
FOD = 125o + 155o = 280o.
Hence, x = 280.
Solution 9(iii)
Through E, draw EF || CD.
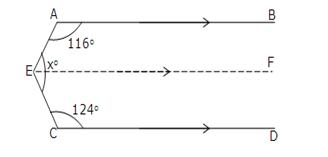
Now since EF || CD and EC is transversal.
![]() FEC +
FEC + ![]() ECD = 180o
ECD = 180o
[sum of consecutive interior angles is 180o]
![]()
![]() FEC + 124o = 180o
FEC + 124o = 180o
![]()
![]() FEC = 180o - 124o = 56o
FEC = 180o - 124o = 56o
Since EF || CD and AB ||CD
So, EF || AB and AE is a trasveral.
So,![]() BAE +
BAE + ![]() FEA = 180o
FEA = 180o
[sum of consecutive interior angles is 180o]
![]() 116o +
116o + ![]() FEA = 180o
FEA = 180o
![]()
![]() FEA = 180o - 116o = 64o
FEA = 180o - 116o = 64o
Thus,xo = ![]() FEA +
FEA + ![]() FEC
FEC
= 64o + 56o = 120o.
Hence, x = 120.
Solution 10
Through C draw FG || AE
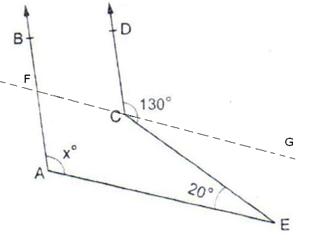
Now, since CG || BE and CE is a transversal.
So, ![]() GCE =
GCE = ![]() CEA = 20o [Alternate angles]
CEA = 20o [Alternate angles]
![]()
![]() DCG = 130o -
DCG = 130o - ![]() GCE
GCE
= 130o - 20o = 110o
Also, we have AB || CD and FG is a transversal.
So, ![]() BFC =
BFC = ![]() DCG = 110o [Corresponding angles]
DCG = 110o [Corresponding angles]
As, FG || AE, AF is a transversal.
![]() BFG =
BFG = ![]() FAE [Corresponding angles]
FAE [Corresponding angles]
![]() xo =
xo = ![]() FAE = 110o.
FAE = 110o.
Hence, x = 110
Solution 11
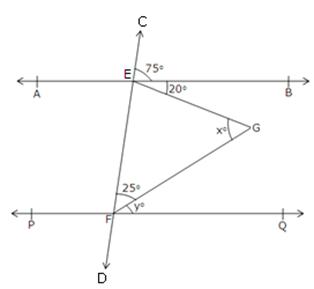
Since AB || PQ and EF is a transversal.
So, ![]() CEB =
CEB = ![]() EFQ [Corresponding angles]
EFQ [Corresponding angles]
![]()
![]() EFQ = 75o
EFQ = 75o
![]()
![]() EFG +
EFG + ![]() GFQ = 75o
GFQ = 75o
![]() 25o + yo = 75o
25o + yo = 75o
![]() y = 75 - 25 = 50
y = 75 - 25 = 50
Also, ![]() BEF +
BEF + ![]() EFQ = 180o [sum of consecutive interior angles is 180o]
EFQ = 180o [sum of consecutive interior angles is 180o]
= 180o - 75o
![]() BEF = 105o
BEF = 105o
![]()
![]() FEG +
FEG + ![]() GEB =
GEB = ![]() BEF = 105o
BEF = 105o
![]()
![]() FEG = 105o -
FEG = 105o - ![]() GEB = 105o - 20o = 85o
GEB = 105o - 20o = 85o
In ![]() EFG we have,
EFG we have,
xo + 25o + ![]() FEG = 180o
FEG = 180o
Hence, x = 70.
Solution 12
Since AB || CD and AC is a transversal.
So, ![]() BAC +
BAC + ![]() ACD = 180o [sum of consecutive interior angles is 180o]
ACD = 180o [sum of consecutive interior angles is 180o]
![]()
![]() ACD = 180o -
ACD = 180o - ![]() BAC
BAC
= 180o - 75o = 105o
![]() ECF =
ECF = ![]() ACD [Vertically opposite angles]
ACD [Vertically opposite angles]
![]()
![]() ECF = 105o
ECF = 105o
Now in ![]() CEF,
CEF,
![]() ECF +
ECF + ![]() CEF +
CEF + ![]() EFC =180o
EFC =180o
![]() x = 180 - 30 - 105 = 45
x = 180 - 30 - 105 = 45
Hence, x = 45.
Solution 13
Since AB || CD and PQ a transversal.
So, ![]() PEF =
PEF = ![]() EGH [Corresponding angles]
EGH [Corresponding angles]
![]()
![]() EGH = 85o
EGH = 85o
![]() EGH and
EGH and ![]() QGH form a linear pair.
QGH form a linear pair.
So, ![]() EGH +
EGH + ![]() QGH = 180o
QGH = 180o
![]()
![]() QGH = 180o - 85o = 95o
QGH = 180o - 85o = 95o
Similarly, ![]() GHQ + 115o = 180o
GHQ + 115o = 180o
![]()
![]() GHQ = 180o - 115o = 65o
GHQ = 180o - 115o = 65o
In ![]() GHQ, we have,
GHQ, we have,
![]()
xo + 65o + 95o = 180o
![]() x = 180 - 65 - 95 = 180 - 160
x = 180 - 65 - 95 = 180 - 160
![]() x = 20
x = 20
Solution 14
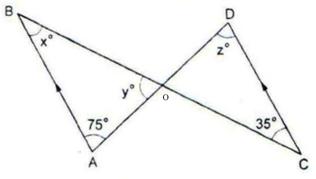
Since AB || CD and BC is a transversal.
So, ![]() ABC =
ABC = ![]() BCD
BCD
![]() x = 35
x = 35
Also, AB || CD and AD is a transversal.
So, ![]() BAD =
BAD = ![]() ADC
ADC
![]() z = 75
z = 75
In ![]() ABO, we have,
ABO, we have,
![]()
![]() xo + 75o + yo = 180o
xo + 75o + yo = 180o
![]() 35 + 75 + y = 180
35 + 75 + y = 180
![]() y = 180 - 110 = 70
y = 180 - 110 = 70
![]() x = 35, y = 70 and z = 75.
x = 35, y = 70 and z = 75.
Solution 16
Through F, draw KH || AB || CD
Now, KF || CD and FG is a transversal.
![]()
![]() KFG =
KFG = ![]() FGD = ro (i)
FGD = ro (i)
[alternate angles]
Again AE || KF, and EF is a transversal.
So,![]() AEF +
AEF + ![]() KFE = 180o
KFE = 180o
![]()
![]() KFE = 180o - po (ii)
KFE = 180o - po (ii)
Adding (i) and (ii) we get,
![]() KFG +
KFG + ![]() KFE = 180 - p + r
KFE = 180 - p + r
![]()
![]() EFG = 180 - p + r
EFG = 180 - p + r
![]() q = 180 - p + r
q = 180 - p + r
i.e.,p + q - r = 180
Solution 17
![]() PRQ = xo = 60o [vertically opposite angles]
PRQ = xo = 60o [vertically opposite angles]
Since EF || GH, and RQ is a transversal.
So, ![]() x =
x = ![]() y [Alternate angles]
y [Alternate angles]
![]() y = 60
y = 60
AB || CD and PR is a transversal.
So, ![]() [Alternate angles]
[Alternate angles]
![]()
![]() [since
[since ![]() ]
]
![]() x +
x + ![]() QRD = 110o
QRD = 110o
![]()
![]() QRD = 110o - 60o = 50o
QRD = 110o - 60o = 50o
In ![]() QRS, we have,
QRS, we have,
![]() QRD + to + yo = 180o
QRD + to + yo = 180o
![]() 50 + t + 60 = 180
50 + t + 60 = 180
![]() t = 180 - 110 = 70
t = 180 - 110 = 70
Since, AB || CD and GH is a transversal
So, zo = to = 70o [Alternate angles]
![]() x = 60 , y = 60, z = 70 and t = 70
x = 60 , y = 60, z = 70 and t = 70
Solution 18
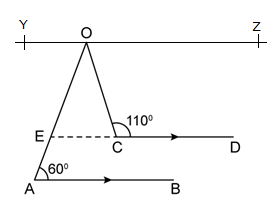
AB ∥ CD and a transversal t cuts them at E and F respectively.
⇒ ∠BEF + ∠DFE = 180° (interior angles)
![]()
⇒ ∠GEF + ∠GFE = 90° ….(i)
Now, in ΔGEF, by angle sum property
∠GEF + ∠GFE + ∠EGF = 180°
⇒ 90° + ∠EGF = 180° ….[From (i)]
⇒ ∠EGF = 90°
Solution 19
Since AB ∥ CD and t is a transversal, we have
∠AEF = ∠EFD (alternate angles)
![]()
⇒ ∠PEF = ∠EFQ
But, these are alternate interior angles formed when the transversal EF cuts EP and FQ.
∴ EP ∥ FQ
Solution 20
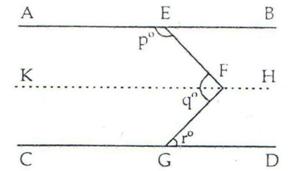
Construction: Produce DE to meet BC at Z.
Now, AB ∥ DZ and BC is the transversal.
⇒ ∠ABC = ∠DZC (corresponding angles) ….(i)
Also, EF ∥ BC and DZ is the transversal.
⇒ ∠DZC = ∠DEF (corresponding angles) ….(ii)
From (i) and (ii), we have
∠ABC = ∠DEF
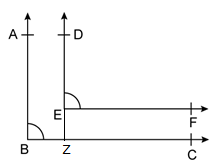
Solution 21
Construction: Produce ED to meet BC at Z.
Now, AB ∥ EZ and BC is the transversal.
⇒ ∠ABZ + ∠EZB = 180° (interior angles)
⇒ ∠ABC + ∠EZB = 180° ….(i)
Also, EF ∥ BC and EZ is the transversal.
⇒ ∠BZE = ∠ZEF (alternate angles)
⇒ ∠BZE = ∠DEF ….(ii)
From (i) and (ii), we have
∠ABC + ∠DEF = 180°
Solution 22
Let the normal to mirrors m and n intersect at P.
Now, OB ⊥ m, OC ⊥ n and m ⊥ n.
⇒ OB ⊥ OC
⇒ ∠APB = 90°
⇒ ∠2 + ∠3 = 90° (sum of acute angles of a right triangle is 90°)
By the laws of reflection, we have
∠1 = ∠2 and ∠4 = ∠3 (angle of incidence = angle of reflection)
⇒ ∠1 + ∠4 = ∠2 + ∠3 = 90°
⇒ ∠1 + ∠2 + ∠3 + ∠4 = 180°
⇒ ∠CAB + ∠ABD = 180°
But, ∠CAB and ∠ABD are consecutive interior angles formed, when the transversal AB cuts CA and BD.
∴ CA ∥ BD
Solution 23
In the given figure,
∠BAC = ∠ACD = 110°
But, these are alternate angles when transversal AC cuts AB and CD.
Hence, AB ∥ CD.
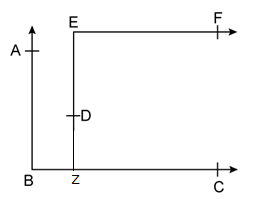
Solution 24
Let the two parallel lines be m and n.
Let p ⊥ m.
⇒ ∠1 = 90°
Let q ⊥ n.
⇒ ∠2 = 90°
Now, m ∥ n and p is a transversal.
⇒ ∠1 = ∠3 (corresponding angles)
⇒ ∠3 = 90°
⇒ ∠3 = ∠2 (each 90°)
But, these are corresponding angles, when transversal n cuts lines p and q.
∴ p ∥ q.
Hence, two lines which are perpendicular to two parallel lines, are parallel to each other.

