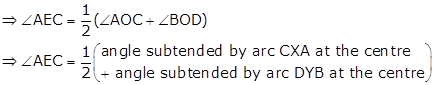Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 12 - Circles
Circles Exercise MCQ
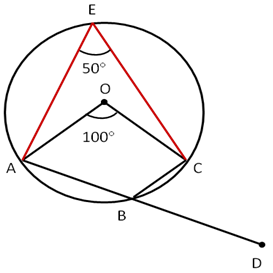
Solution 1
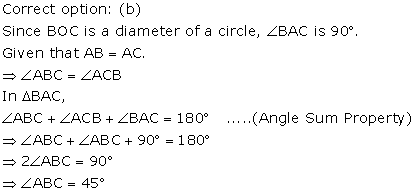
Correct option: (b)

Solution 2
Correct option: (c)

Solution 3
Solution 4

Solution 5

Solution 6
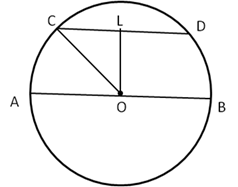

Solution 7
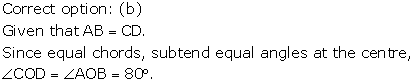
Solution 8

Solution 9
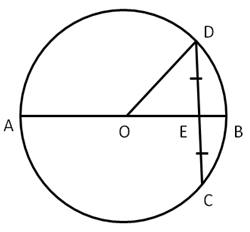

Solution 10

Solution 11
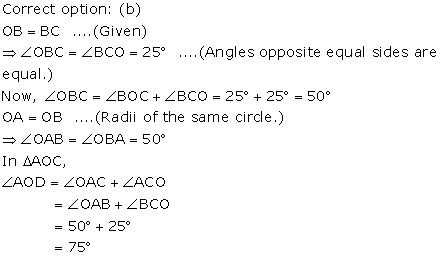
Solution 12

Solution 13
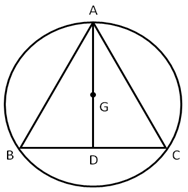

Solution 14
![]()
Solution 15
![]()
Solution 16
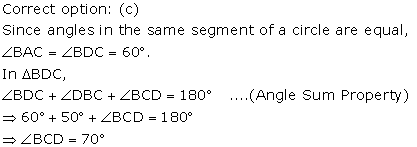
Solution 17

Solution 18
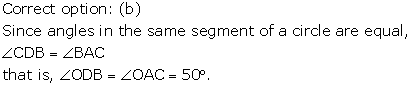
Solution 19
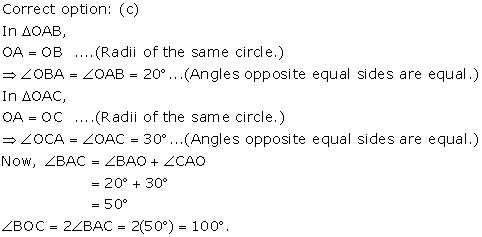
Solution 20

Solution 21

Solution 22

Solution 23

Solution 24
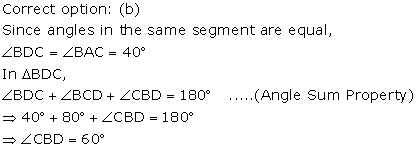
Solution 25
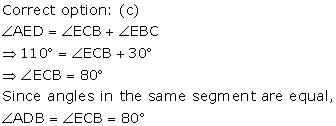
Solution 26

Solution 27

Solution 28
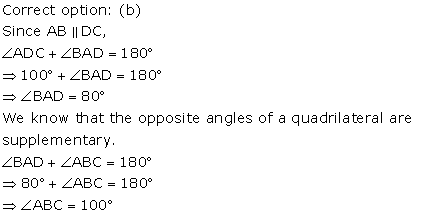
Solution 29

Solution 30

Solution 31
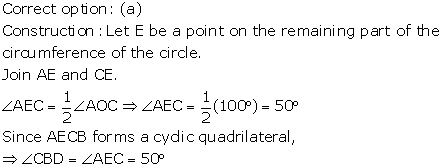
Solution 32

Solution 33

Solution 34
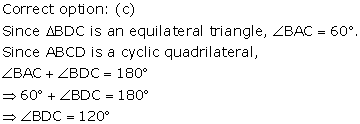
Solution 35
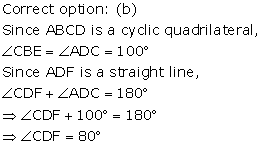
Solution 36

Solution 37

Solution 38

Solution 39

Solution 40

Solution 41

Solution 42
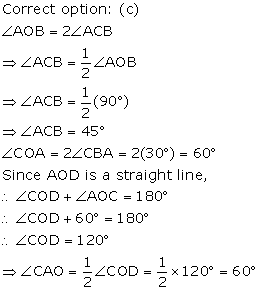
Circles Exercise Ex. 12C
Solution 1
Solution 2
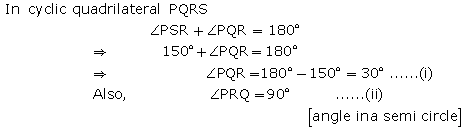
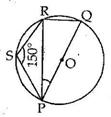
Solution 3

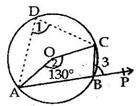
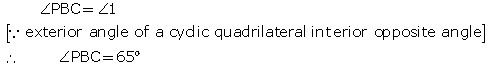
Solution 4
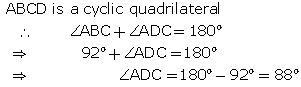
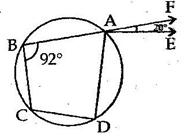
Solution 5
![]()

Solution 6
Solution 7
Solution 8

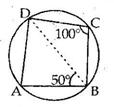

Solution 9
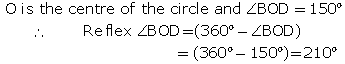
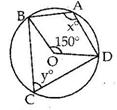
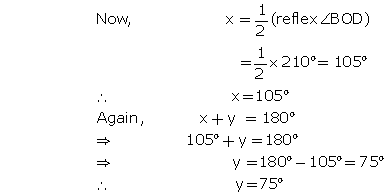
Solution 10
Solution 11

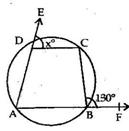
Solution 12
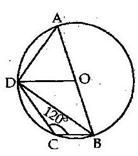
Solution 13
Solution 14
Solution 15

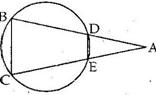
Solution 16
Solution 17
Solution 18
![]()
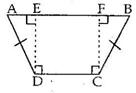
Solution 19

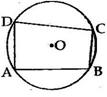
Solution 20

![]()
![]()
![]()
Solution 21


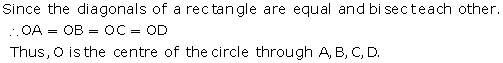
Solution 22



![]()
Solution 23

Solution 24

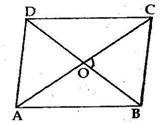
Solution 25
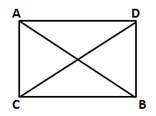
AB is the common hypotenuse of ΔACB and ΔADB.
⇒ ∠ACB = 90° and ∠BDC = 90°
⇒ ∠ACB + ∠BDC = 180°
⇒ The opposite angles of quadrilateral ACBD are supplementary.
Thus, ACBD is a cyclic quadrilateral.
This means that a circle passes through the points A, C, B and D.
⇒ ∠BAC = ∠BDC (angles in the same segment)
Solution 26
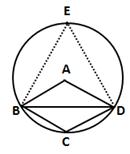
Construction: Take a point E on the circle. Join BE, DE and BD.
We know that the angle subtended by an arc of a circle at its centre is twice the angle subtended by the same arc at a point on the circumference.
⇒ ∠BAD = 2∠BED
![]()
Now, EBCD is a cyclic quadrilateral.
⇒ ∠BED + ∠BCD = 180°
⇒ ∠BCD = 180° - ∠BED
![]()
In ΔBCD, by angle sum property
∠CBD + ∠CDB + ∠BCD = 180°
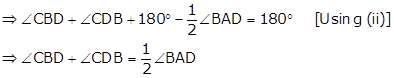
Circles Exercise Ex. 12A
Solution 1
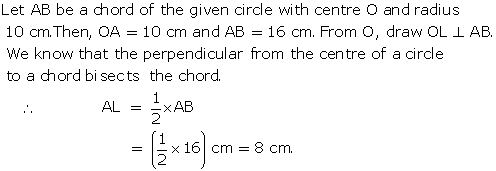

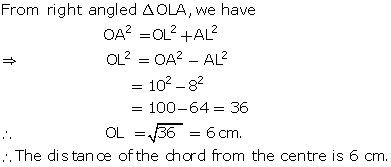
Solution 2

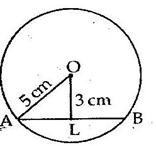
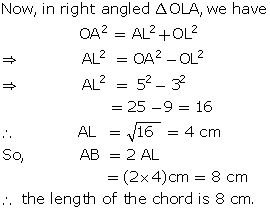
Solution 3
![]()
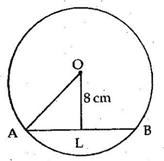
![]()

Solution 4

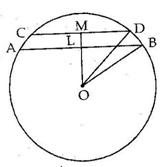
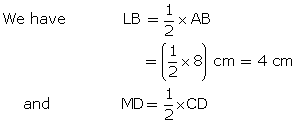
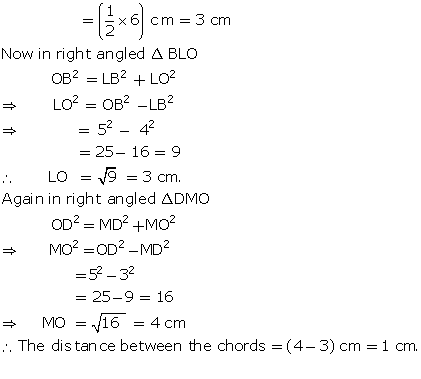

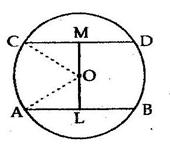


Solution 5
![]()
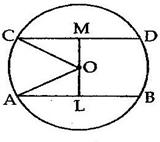

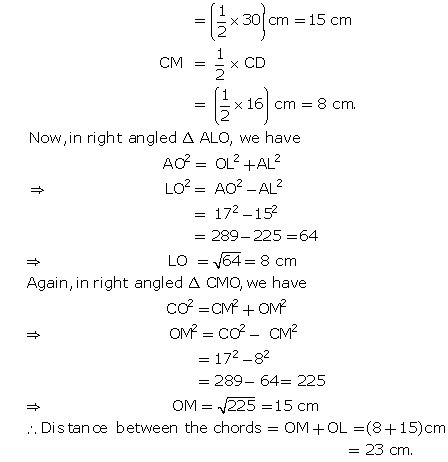
Solution 6
![]()
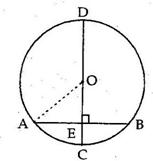
![]()

Solution 7
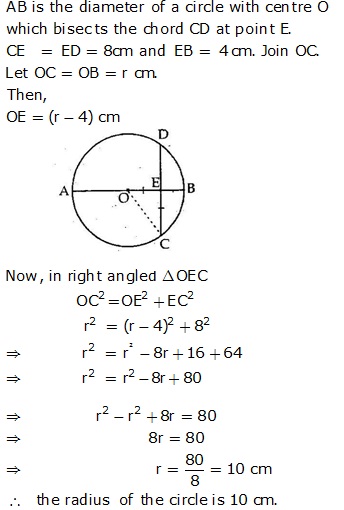
Solution 8
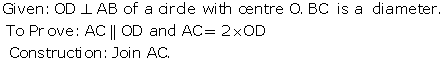

Solution 9


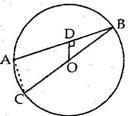
Solution 10
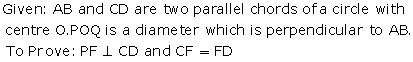
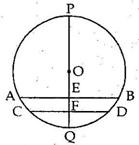

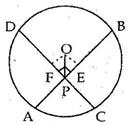
Solution 11

Solution 12

Solution 13
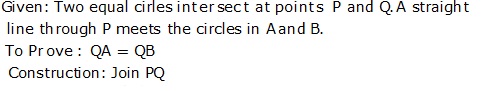


Solution 14

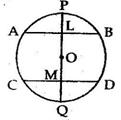
Solution 15
Solution 16

Solution 17

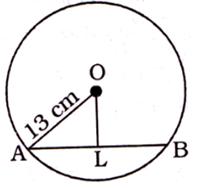
Let O be the centre of a circle with radius r.
⇒ OB = OC = r
Let AC = x
Then, AB = 2x
Let OM ⊥ AB
⇒ OM = p
Let ON ⊥ AC
⇒ ON = q
In ΔOMB, by Pythagoras theorem,
OB2 = OM2 + BM2
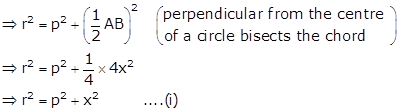
In ΔONC, by Pythagoras theorem,
OC2 = ON2 + CN2
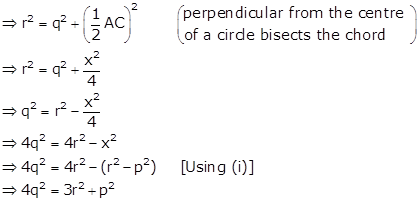
Solution 18
![]()
Solution 19
Solution 20
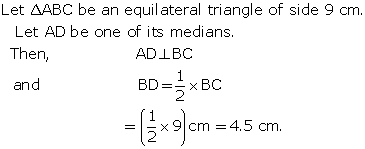

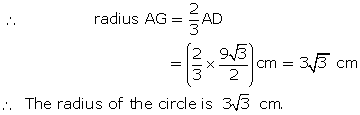
Solution 21
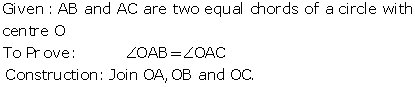

Solution 22
Solution 23
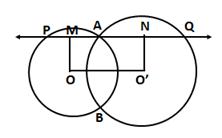
Draw OM ⊥ PQ and O'N ⊥ PQ
⇒ OM ⊥ AP
⇒ AM = PM (perpendicular from the centre of a circle bisects the chord)
⇒ AP = 2AM ….(i)
And, O'N ⊥ PQ
⇒ O'N ⊥ AQ
⇒ AN = QN (perpendicular from the centre of a circle bisects the chord)
⇒ AQ = 2AN ….(ii)
Now,
PQ = AP + PQ
⇒ PQ = 2AM + 2AN
⇒ PQ = 2(AM + AN)
⇒ PQ = 2MN
⇒ PQ = 2OO' (since MNO'O is a rectangle)
Circles Exercise Ex. 12B
Solution 1
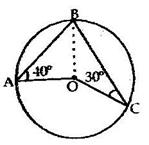
Solution 2
Solution 3
Solution 4
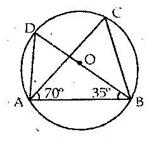
Solution 5
Solution 6

Solution 7

Solution 8
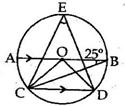
Solution 9
Solution 10
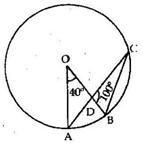
Solution 11
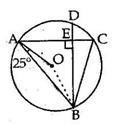
Solution 12
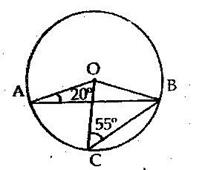
Solution 13
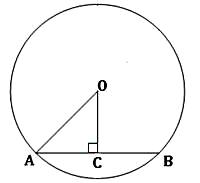
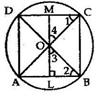
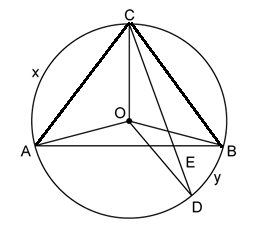
Given, ∠AOD = 90° and ∠OEC = 90°
⇒ ∠AOD = ∠OEC
But ∠AOD and ∠OEC are corresponding angles.
⇒ OD || BC and OC is the transversal.
∴ ∠DOC = ∠OCE (alternate angles)
⇒ ∠DOC = 30° (since ∠OCE = 30°)
We know that the angle subtended by an arc of a circle at its centre is twice the angle subtended by the same arc at a point on the circumference.
⇒ ∠DOC = 2∠DBC

Now, ∠ABE = ∠ABC = ∠ABD + ∠DBC = 45° + 15° = 60°
In ΔABE,
∠BAE + ∠AEB + ∠ABE = 180°
⇒ x + 90° + 60° = 180°
⇒ x + 150° = 180°
⇒ x = 30°
Solution 14
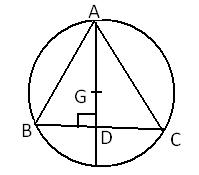
Construction: Join AC
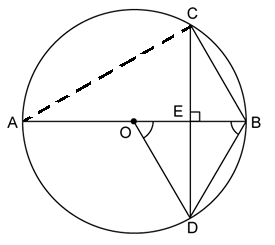
Given, BD = OD
Now, OD = OB (radii of same circle)
⇒ BD = OD = OB
⇒ ΔODB is an equilateral triangle.
⇒ ∠ODB = 60°
We know that the altitude of an equilateral triangle bisects the vertical angle.
![]()
Now, ∠CAB = ∠BDC (angles in the same segment)
⇒ ∠CAB = ∠BDE = 30°
Solution 15
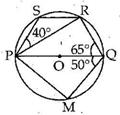
Solution 16
We know that the angle subtended by an arc of a circle at its centre is twice the angle subtended by the same arc at a point on the circumference.
⇒ ∠APB = 2∠ACB
![]()
Now, ACD is a straight line.
⇒ ∠ACB + ∠DCB = 180°
⇒ 75° + ∠DCB = 180°
⇒ ∠DCB = 105°
Again,
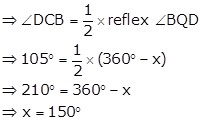
Solution 17
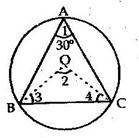
Solution 18
Join AC and BC
We know that the angle subtended by an arc of a circle at its centre is twice the angle subtended by the same arc at a point on the circumference.
⇒ ∠AOC = 2∠ABC ….(i)
Similarly, ∠BOD = 2∠BCD ….(ii)
Adding (i) and (ii),
∠AOC + ∠BOD = 2∠ABC + 2∠BCD
⇒ ∠AOC + ∠BOD = 2(∠ABC + ∠BCD)
⇒ ∠AOC + ∠BOD = 2(∠EBC + ∠BCE)
⇒ ∠AOC + ∠BOD = 2(180° - ∠CEB)
⇒ ∠AOC + ∠BOD = 2(180° - [180° - ∠AEC])
⇒ ∠AOC + ∠BOD = 2∠AEC