Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 16 - Presentation of Data in Tabular Form
Presentation of Data in Tabular Form Exercise MCQ
Solution 1
Correct option: (d)
Range = maximum value - minimum value
= 32 - 6
= 26
Solution 2

Solution 3
![]()
Solution 4

Solution 5

Solution 6

Solution 7

Solution 8
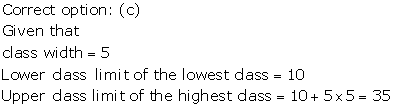
Solution 9
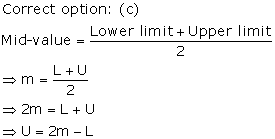
Presentation of Data in Tabular Form Exercise Ex. 16
Solution 1
Statistics is a branch of science which deals with the collection, presentation, analysis and interpretation of numerical data.
Solution 2
Fundamental characteristics of statistics :
(i) It deals only with the numerical data.
(ii) Qualitative characteristic such as illiteracy, intelligence, poverty etc cannot be measured numerically
(iii) Statistical inferences are not exact.
Solution 3
Primary data: Primary data is the data collected by the investigator himself with a definite plan in his mind. These data are very accurate and reliable as these being collected by the investigator himself.
Secondary Data: Secondary data is the data collected by a person other than the investigator.
Secondary Data is not very reliable as these are collected by others with purpose other than the investigator and may not be fully relevant to the investigation.
Solution 4
(i)Variate : Any character which can assume many different values is called a variate.
(ii)Class Interval :Each group or class in which data is condensed is calleda class interval.
(iii)Class-Size :The difference between the true upper limitand the true lower limit of a class is called class size.
(iv)Classmark : The average of upper and lower limit of a class interval is called its class mark.
i.e Class mark=![]()
(v) Class limit: Class limits are the two figures by which a class is bounded . The figure on the left side of a class is called lower lower limit and on the right side is called itsupper limit.
(vi)True class limits: In the case of exclusive form of frequency distribution, the upper class limits and lower classlimits are the true upper limits and thetrue lower limits. But in the case of inclusive form of frequency distribution , the true lower limit of a class is obtained by subtracting 0.5 from the lower limit of the class. And the true upper limit of the class is obtained by adding 0.5 to the upper limit.
(vii)Frequency of a class : The number of observations falling in aclass determines its frequency.
(viii)Cumulative frequency of a class: The sum of all frequenciesup to and including that class is called , the cumulative frequency of that class.
Solution 5
(i) Frequency Distribution Table:
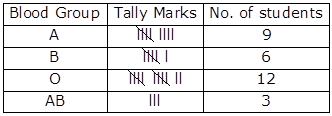
(ii) The most common blood group is 'O' and the rarest blood group is 'AB'.
Solution 6
Frequency Distribution Table:
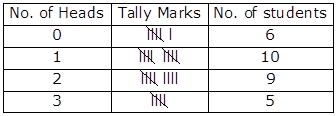
Solution 7
Thus , the frequency distribution may be given as under:
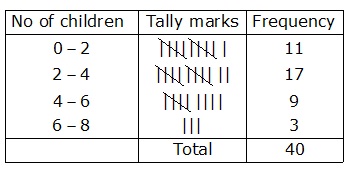
Solution 8
(i) Grouped Frequency Distribution Table:
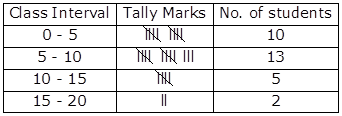
(ii) 2 children watch television for 15 or more hours a week.
Solution 9
Minimum observation is 1 and minimum observation is 24. The classes of equal size converging the given data are : (0-5), (5-10), (10-15), (15-20), (20-25)
Thus, the frequency distribution may be given as under :
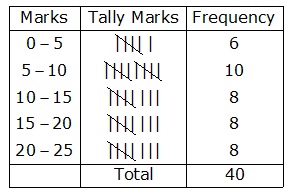
Solution 10
Grouped Frequency Distribution Table:
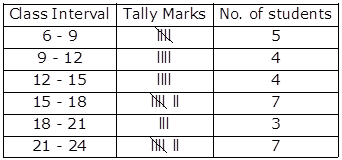
Solution 11
Minimum observation is 210 and maximum observation =320
So the range is (320-210)=110
The classes of equal size covering the given data are :
(210-230), (230-250), (250-270) , (270-290), (290-310), (310-330)
Thus the frequency distribution may be given as under :
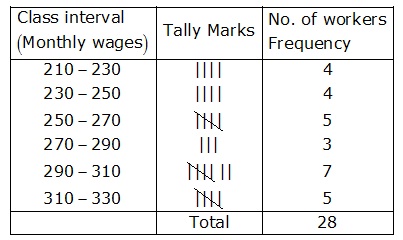
Solution 12
Minimum observation is 30 and maximum observation is 110
So, range is 100-30=80
The classes of equal size covering the given data are :
(30-40) ,(40-50) , (50-60) ,(60-70) , (70-80), (80-90),(90-100),(100-110), (110-120)
Thus , the frequency and cumulative frequency table may be given as under :
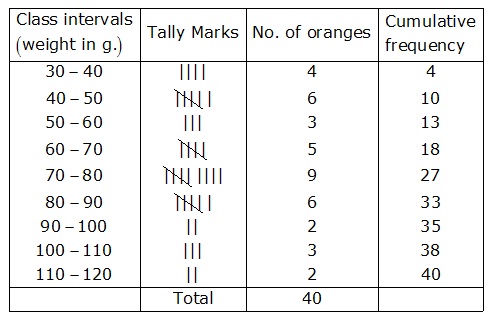
Solution 13
Grouped Frequency Distribution Table and Cumulative Frequency Table:
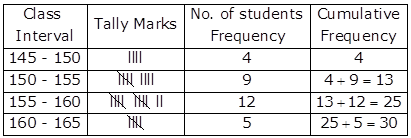
Solution 14
|
Age (in years) (age) |
No of patients (Frequency) |
Cumulative Frequency |
|
10-20 20-30 30-40 40-50 50-60 60-70 |
90 50 60 80 50 30 |
90 140 200 280 330 360 |
|
Total |
360 |
|
Solution 15
|
Marks (below) |
No of students(Cumulative Frequency.) |
Class Intervals |
Frequency |
|
10 20 30 40 50 60
|
5 12 32 40 45 48
|
0-10 10-20 20-30 30-40 40-50 50-60
|
5 12 - 5 = 7 32 - 12 = 20 40 - 32 = 8 45 - 40 = 5 48 - 45 = 3 |
|
|
|
Total |
48
|
Solution 16
|
Marks (below) |
No of students(Cumulative Frequency) |
Class Intervals |
Frequency |
|
10 20 30 40 50 60
|
17 22 29 37 50 60 |
0-10 10-20 20-30 30-40 40-50 50-60
|
17 22 - 17 = 5 29 - 22 = 7 37 - 29 = 8 50 - 37 = 13 60 - 50 = 10 |
|
|
|
Total |
60
|
Solution 17
|
Marks (below) |
No of student s(C.F.) |
Class Intervals |
Frequency |
|
More than 60 More than 50 More than 40 More than 30 More than 20 More than 10 More than 0
|
0 16 40 75 87 92 100 |
More than 60 50-60 40-50 30-40 20-30 10-20 0-10 |
0 16-0=16 40-16=24 75-40=35 87-75=12 92-87=5 100-92=8
|
|
|
|
Total |
100
|
Solution 18
Arranging data in ascending order, we have
46, 48, 49, 64, 65, 66, 68, 72, 76, 79, 82, 82, 90, 91, 96, 100, 100
Minimum marks = 46
Maximum Marks = 100
∴ Range of the above data = Maximum Marks - Minimum Marks
= 100 - 46
= 54
Solution 19
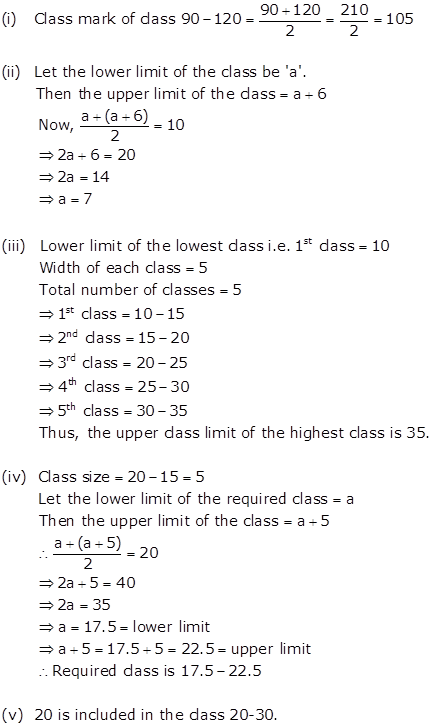
Solution 20
|
Height (in cm) |
Frequency |
Cumulative frequency |
|
160-165 |
15 |
a = 15 |
|
165-170 |
b = 35 - 15 = 20 |
35 |
|
170-175 |
12 |
c = 35 + 12 = 47 |
|
175-180 |
d = 50 - 47 = 3 |
50 |
|
180-185 |
e = 55 - 50 = 5 |
55 |
|
185-190 |
5 |
f = 55 + 5 = 60 |
|
|
g = 60 |
|

