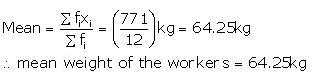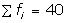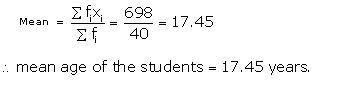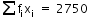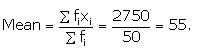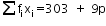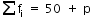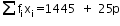Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 18 - Mean, Median and Mode of Ungrouped Data
Mean, Median and Mode of Ungrouped Data Exercise MCQ
Solution 1

Solution 2

Solution 3

Solution 4
Correct option: (b)
If each observation of the data is decreased by 8 then their mean is also decreased by 8.
Solution 5
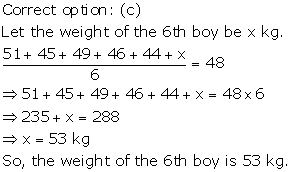
Solution 6

Solution 7

Solution 8
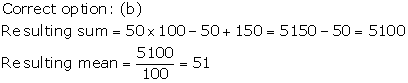
Solution 9

Solution 10

Solution 11

Solution 12
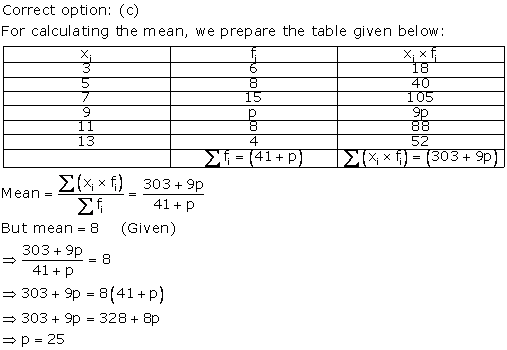
Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Mean, Median and Mode of Ungrouped Data Exercise Ex. 18A
Solution 1(iv)
Factors of 20 are: 1,2,4,5,10,20
![]()
![]()
Solution 1(iii)
First seven multiples of 5 are: 5,10,15, 20, 25, 30, 35
![]()

Therefore, Mean =20
Solution 1(ii)
First ten odd numbers are:
1,3,5,7,9,11,13,15, 17, and 19
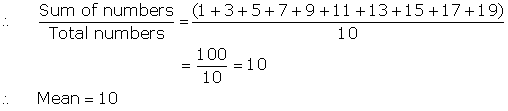
Solution 1(i)
first eight natural numbers are:
1,2,3,4,5,6,7and 8
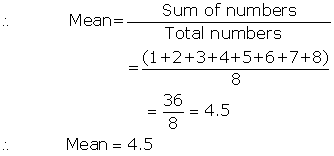
Solution 1(v)
Prime numbers between 50 and 80 are as follows:
53, 59, 61, 67, 71, 73, 79
Total prime numbers between 50 and 80 = 7

Solution 2
Solution 3
Sol.3
![]()
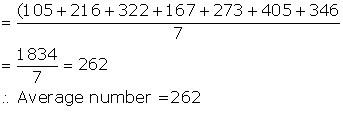
Solution 4
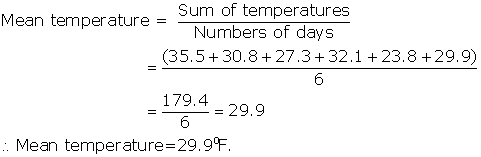
Solution 5
Total numbers of observations = 5
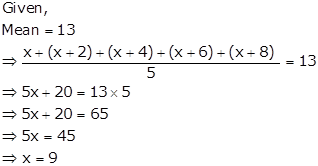
Thus, last three observations are (9 + 4), (9 + 6) and (9 + 8),
i.e. 13, 15 and 17
![]()
Solution 6
Mean weight of the boys =48 kg
![]()
Sum of the weight of6 boys =(48x6)kg =288kg
Sum of the weights of 5 boys=(51+45+49+46+44)kg=235kg
Weight of the sixth boy=(sum of the weights of 6 boys ) - (sum of the weights of 5 boys)
=(288-235)=53kg.
![]()
Solution 7
Calculated mean marks of 50 students =39
![]() calculated sum of these marks=(39x 50)=1950
calculated sum of these marks=(39x 50)=1950
Corrected sum of these marks
=[1950-(wrong number)+(correct number)]
=(1950-23+43) =1970
![]() correct mean =
correct mean =![]()
Solution 8
Let the given numbers be x1,X2......X24

Solution 9
Let the given numbers be x1, x2.....x20
Then , the mean of these numbers =
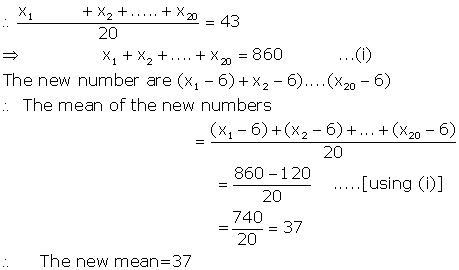
Solution 10
Let the given numbers be x1, x2.......x15
Then the mean of these numbers=27
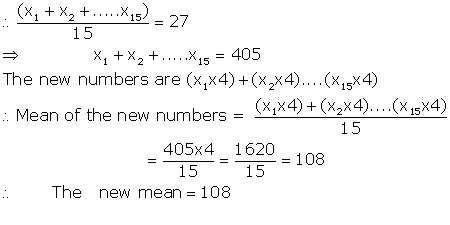
Solution 11
Solution 12
Solution 13
Mean of 6 numbers = 23
Sum of 6 numbers =(23x6 )=138
Again , mean of 5 numbers =20
Sum of 5 numbers=(20x 5 ) =100
![]() The excluded number= (sum of 6 numbers
)-(sum of 5 numbers)
The excluded number= (sum of 6 numbers
)-(sum of 5 numbers)
=(138-100) =38
![]() The excluded number=38.
The excluded number=38.
Solution 14
Mean height of 30 boys = 150 cm
⇒ Total height of 30 boys = 150 × 30 = 4500 cm
Correct sum = 4500 - incorrect value + correct value
= 4500 - 135 + 165
= 4530
![]()
Solution 15
Mean weight of 34 students = 46.5 kg
Total weight of 34 students =(34x46.5)kg =1581 kg
Mean weight of 34 students and the teacher =(46.5+0.5)kg=47kg ![]()
![]() Total weight of 34 students and the teacher
Total weight of 34 students and the teacher
=(47x35)kg =1645kg
![]() Weight of the teacher =(1645-1581)kg= 64kg
Weight of the teacher =(1645-1581)kg= 64kg
Solution 16
Mean weight of 36 students = 41 kg
Total weight of 36 students = 41x 36 kg = 1476kg
One student leaves the class mean is decreased by 200 g.
![]() New mean =(41-0.2)kg = 40.8 kg
New mean =(41-0.2)kg = 40.8 kg ![]()
Total weight of 35 students = 40.8x35 kg = 1428 kg.
![]() the weight of the student who left =(1476-1428)kg =48 kg.
the weight of the student who left =(1476-1428)kg =48 kg.
Solution 17
Mean weight of 39 students =40 kg
Total weight of 39 students = 40x 39) = 1560 kg
One student joins the class mean is decreased by 200 g.
![]() New mean =(40-0.2)kg = 39.8 kg
New mean =(40-0.2)kg = 39.8 kg ![]()
Total weight of 40 students =(39.8x40)kg=1592 kg.
![]() the weight of new student
the weight of new student
= Total weight of 40 students - Total weight of 39 students
= 1592-1560 = 32 kg
Solution 18
The increase in the average of 10 oarsmen = 1.5 kg
![]() Total weight increased =(1.5x10) kg=15 kg
Total weight increased =(1.5x10) kg=15 kg
Since the man weighing 58 kg has been replaced,
Weight of the new man =(58+15)kg =73kg.
Solution 19
Mean of 8 numbers=35
Total sum of 8 numbers = 35x8 = 280
Since One number is excluded, New mean = 35 - 3 = 32
![]() Total sum of 7 numbers = 32x7 = 224
Total sum of 7 numbers = 32x7 = 224
![]() the excluded number = Sum of 8 numbers - Sum of 7 numbers
the excluded number = Sum of 8 numbers - Sum of 7 numbers
= 280 - 224 = 56
Solution 20
Mean of 150 items = 60
Total Sum of 150 items = 150x60 = 9000
![]() Correct sum of items =[(sum of 150 items)-(sum of wrong items)+(sum of right items)]
Correct sum of items =[(sum of 150 items)-(sum of wrong items)+(sum of right items)]
= [9000 - (52 + 8) + (152 + 88)]
= [9000-(52+8)+(152+88)]
= 9180
![]() Correct mean =
Correct mean =![]()
Solution 21
Mean of 31 results=60
Total sum of 31 results = 31x60 = 1860
Mean of the first 16 results =16x58=928
Total sum of the first 16 results=16x58=928
Mean of the last 16 results=62
Total sum of the last 16 results=16x62=992
![]() The 16th result = 928 + 992 - 1860
The 16th result = 928 + 992 - 1860
= 1920 - 1860 = 60
![]() The 16th result = 60.
The 16th result = 60.
Solution 22
Mean of 11 numbers = 42
Total sum of 11 numbers = 42x11 = 462
Mean of the first 6 numbers = 37
Total sum of first 6 numbers = 37x6 = 222
Mean of the last 6 numbers = 46
Total sum of last 6 numbers = 6x46 = 276
![]() The 6th number= 276 + 222 - 462
The 6th number= 276 + 222 - 462
= 498 - 462 = 36
![]() The 6th number = 36
The 6th number = 36
Solution 23
Mean weight of 25 students = 52kg
Total weight of 25 students = 52x25 kg=1300 kg
Mean of the first 13 students = 48 kg
Total weight of the first 13 students = 48x13 kg = 624kg
Mean of the last 13 students = 55 kg
Total weight of the last 13 students = 55x13 kg = 715 kg
![]() The weight of 13th student
The weight of 13th student
= Total weight of the first 13 students + Total weight of the last 13 students - Total weight of 25 students
= 624+715-1300 kg
= 39 kg.
Therefore, the weight of 13th student is 39 kg.
Solution 24
Mean score of 25 observations = 80
Total score of 25 observations = 80x25 = 2000
Mean score of 55 observations = 60
Total score of 55 observations = 60x55 =3300
Total no. of observations = 25+55 =80 observations
![]() Total score = 2000+3300 = 5300
Total score = 2000+3300 = 5300
![]() Mean score =
Mean score =![]()
Solution 25
Average marks of 4 subjects = 50
Total marks of 4 subjects = 50x4 = 200
![]() 36 + 44 + 75 + x = 200
36 + 44 + 75 + x = 200
![]() 155 + x = 200
155 + x = 200
![]() x = 200 - 155 = 45
x = 200 - 155 = 45
![]() The value of x = 45
The value of x = 45
Solution 26
Let the distance of mark from the staring point be x km.
Then , time taken by the ship reaching the marks=![]()
![]()
Time taken by the ship reaching the starting point from the marks =![]()
Total time taken =![]()
Total distance covered =x+x=2x km.

Solution 27
Total number of students = 50
Total number of girls = 50-40 = 10
Average weight of the class = 44 kg
Total weight of 50 students= 44x 50 kg = 2200kg
Average weight of 10 girls = 40 kg
Total weight of 10 girls = 40x10 kg = 400 kg
![]() Total weight of 40 boys = 2200-400 kg =1800 kg
Total weight of 40 boys = 2200-400 kg =1800 kg
![]() the average weight of the boys =
the average weight of the boys = ![]()
Solution 28
Total earnings of the year
= Rs. (3 × 18720 + 4 × 20340 + 5 ×21708 + 35340)
= Rs. (56160 + 81360 + 108540 + 35340)
= Rs. 281400
Number of months = 12
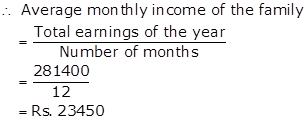
Solution 29
Average weekly payment of 75 workers = Rs. 5680
⇒ Total weekly payment of 75 workers = Rs. (75 × 5680) = Rs. 426000
Mean weekly payment of 25 workers = Rs. 5400
⇒ Total weekly payment of 25 workers = Rs. (25 × 5400) = Rs. 135000
Mean weekly payment of 30 workers = Rs. 5700
⇒ Total weekly payment of 30 workers = Rs. (30 × 5700) = Rs. 171000
Number of remaining workers = 75 - 25 - 30 = 20
Therefore, Total weekly payment of remaining 20 workers
= Rs. (426000 - 135000 - 171000)
= Rs. 120000
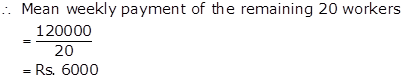
Solution 30
Let the ratio of number of boys to the number of girls be x : 1.
Then,
Sum of marks of boys = 70x
Sum of marks of girls = 73 × 1 = 73
And, sum of marks of boys and girls = 71 × (x + 1)
⇒ 70x + 73 = 71(x + 1)
⇒ 70x + 73 = 71x + 71
⇒ x = 2
Hence, the ratio of number of boys to the number of girls is 2 : 1.
Solution 31
Mean monthly salary of 20 workers = Rs. 45900
⇒ Total monthly salary of 20 workers = Rs. (20 × 45900) = Rs. 918000
Mean monthly salary of 20 workers + manager = Rs. 49200
⇒ Total monthly salary of 20 workers + manager = Rs. (21 × 49200) = Rs. 1033200
Therefore, manager's monthly salary = Rs. (1033200 - 918000) = Rs. 115200
Mean, Median and Mode of Ungrouped Data Exercise Ex. 18C
Solution 1(i)
Arranging the data in accending order, we have
2,2,3, 5, 7, 9, 9, 10, 11
Here n = 9, which is odd
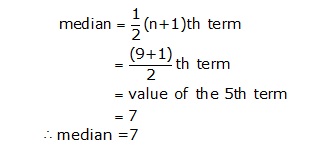
Solution 1(ii)
Arranging the data in ascending order , we have
6, 8, 9, 15, 16, 18, 21, 22, 25
Here n = 9, which is odd

Solution 1(iii)
Arranging data in ascending order:
6, 8, 9, 13, 15, 16, 18, 20, 21, 22, 25
Here n = 11 odd

Solution 1(iv)
Arranging the data in ascending order , we have
0, 1, 2, 2, 3, 4, 4, 5, 5, 7, 8, 9, 10
Here n = 13, which is odd

Solution 2(iii)
Arranging the data in ascending order , we have
3, 4, 9, 10, 12, 15, 17, 27, 47, 48, 75, 81 Here n = 12, which is even

Solution 2(ii)
Arranging the data in ascending order , we have
29, 35, 51, 55, 60, 63, 72, 82, 85, 91
Here n = 10, which is even
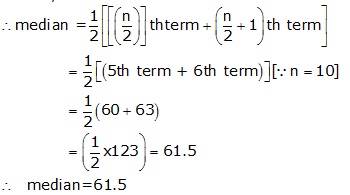
Solution 2(i)
Arranging the data in ascending order , we have
9, 10, 17, 19, 21, 22, 32, 35
Here n = 8, which is even
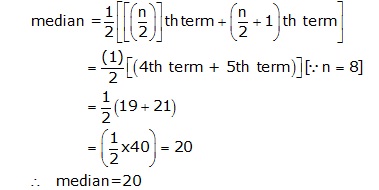
Solution 3
Arranging the data in ascending order , we have
17, 17, 19, 19, 20, 21, 22, 23, 24, 25, 26, 29, 31, 35, 40
Here n = 15, which is odd
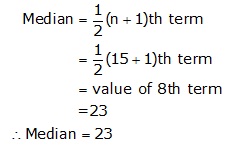
Thus, the median score is 23.
Solution 4
Total number of students = n = 9 (odd)
Arranging heights (in cm) in ascending order, we have
144, 145, 147, 148, 149, 150, 152, 155, 160

Solution 5
Arranging the weights of 8 children in ascending order, we have
9.8, 10.6, 12.7, 13.4, 14.3, 15, 16.5, 17.2
Here , n= 8 , which is even

Solution 6
Arranging the ages of teachers in ascending order , we have
32, 34, 36, 37, 40, 44, 47, 50, 53, 54
Here, n =10, which is even
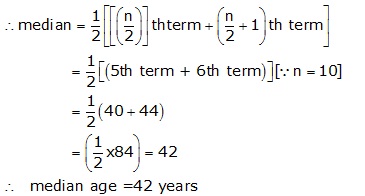
Solution 7
The ten observations in ascending order:
10, 13, 15, 18, x+1, x+3, 30, 32, 35, 41
Here, n =10, which is even

Solution 8
Total number of observations = n = 10 (even)
Median = 65

Solution 9
Total number of observations = n = 8 (even)
Median = 25
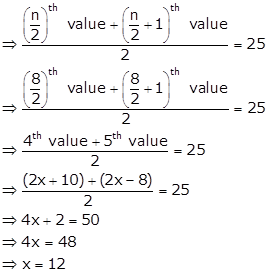
Solution 10
Total number of observations = n = 11 (odd)
Arranging data in ascending order, we have
33, 35, 41, 46, 55, 58, 64, 77, 87, 90, 92
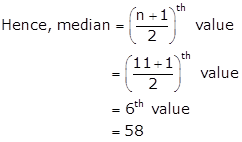
Now, 41 and 55 are replaced by 61 and 75 respectively.
Arranging new data in ascending order, we have
33, 35, 46, 58, 61, 64, 75, 77, 87, 90, 92

Mean, Median and Mode of Ungrouped Data Exercise Ex. 18D
Solution 1
Arrange the given data in ascending order we have
0, 0, 1, 2, 3, 4, 5, 5, 6, 6, 6, 6
Let us prepare the following table:
|
Observations(x) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Frequency |
2 |
1 |
1 |
1 |
1 |
2 |
4 |
As 6 ocurs the maximum number of times i.e. 4, mode = 6
Solution 2
Arranging the given data in ascending order , we have:
15, 20, 22, 23, 25, 25, 25, 27, 40
The frequency table of the data is :
|
Observations(x) |
15 |
20 |
22 |
23 |
25 |
27 |
40 |
|
Frequency |
1 |
1 |
1 |
1 |
3 |
1 |
1 |
As 25 ocurs the maximum number of times i.e. 3, mode = 25
Solution 3
Arranging the given data in ascending order , we have:
1, 1, 2, 3, 3, 4, 5, 5, 6, 6, 7, 8, 9, 9, 9, 9, 9,
The frequency table of the data is :
|
Observations(x) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Frequency |
2 |
1 |
2 |
1 |
2 |
2 |
1 |
1 |
5 |
As 9, occurs the maximum number of times i.e. 5, mode = 9
Solution 4
Arranging the given data in ascending order , we have:
9, 19, 27, 28, 30, 32, 35, 50, 50, 50, 50, 60
The frequency table of the data is :
|
Observations(x) |
9 |
19 |
27 |
28 |
30 |
32 |
35 |
50 |
60 |
|
Frequency |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
4 |
1 |
As 50, ocurs the maximum number of times i.e. 4, mode = 50
Thus, the modal score of the cricket player is 50.
Solution 5
Total number of observations = n = 7
Mean = 18

Thus, data is as follows:
3, 21, 25, 17, 24, 19, 17
The most occurring value is 17.
Hence, the mode of the data is 17.
Solution 6
Number of values = n = 9 (odd)
Numbers in ascending order:
52, 53, 54, 54, (2x + 1), 55, 55, 56, 57

Thus, we have
52, 53, 54, 54, 55, 55, 55, 56, 57
The most occurring number is 55.
Hence, the mode of the data is 55.
Solution 7
Mode of the data = 25
So, we should have the value 25 occurring maximum number of times in the given data.
That means, x + 3 = 25
⇒ x = 22
Thus, we have 24, 15, 40, 23, 27, 26, 22, 25, 20, 25.
Arranging data in ascending order, we have
15, 20, 22, 23, 24, 25, 25, 26, 27, 40
Number of observations = 10 (even)
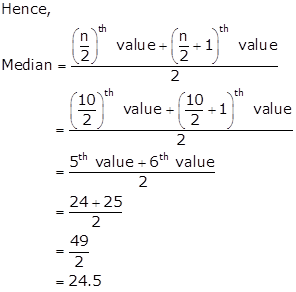
Solution 8
Total number of observations = n = 9 (odd)
Median = 45
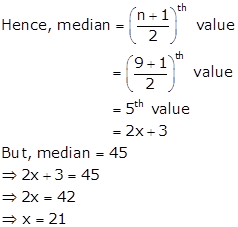
Thus, we have
42, 43, 44, 44, 45, 45, 45, 46, 47
The most occurring value is 45.
Hence, the mode of the data is 45.
Mean, Median and Mode of Ungrouped Data Exercise Ex. 18B
Solution 1
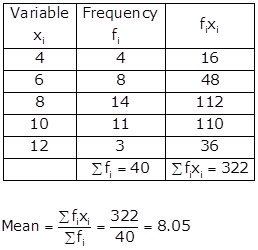
Solution 2
For calculating the mean , we prepare the following frequency table :
|
Weight (in kg) (Xi) |
No of workers (fi) |
fiXi |
|
60 63 66 69 72
|
4 3 2 2 1 |
240 189 132 138 72 |
|
|
|
771 |
Solution 3
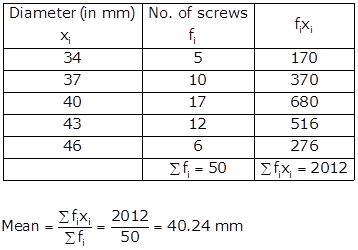
Solution 4
For calculating the mean , we prepare the following frequency table :
|
Age (in years) (Xi) |
Frequency (fi) |
fiXi |
|
15 16 17 18 19 20 |
3 8 9 11 6 3 |
45 128 153 198 114 60 |
|
|
|
698 |
Solution 5
For calculating the mean , we prepare the following frequency table :
|
Variable (Xi) |
Frequency (fi) |
fiXi |
|
10 30 50 70 89 |
7 8 10 15 10 |
70 240 500 1050 890 |
|
|
|
|
Solution 6
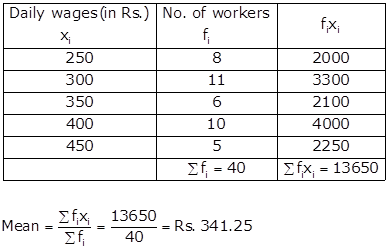
Solution 7
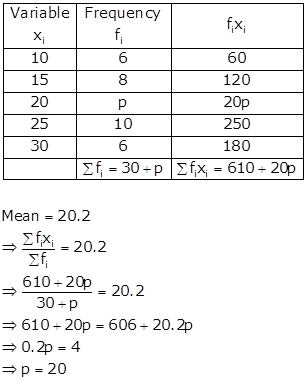
Solution 8
We prepare the following frequency table :
|
(Xi) |
(fi) |
fiXi |
|
3 5 7 9 11 13 |
6 8 15 P 8 4
|
18 40 105 9P 88 52 |
|
|
|
|

![]() 303 + 9p = 8(41+p)
303 + 9p = 8(41+p)
![]() 303 + 9p= 328 + 8p
303 + 9p= 328 + 8p
![]() 9p - 8p = 328 -303
9p - 8p = 328 -303
![]() P=25
P=25
![]() the value of P=25
the value of P=25
Solution 9
We prepare the following frequency distribution table:
|
(Xi) |
(fi) |
fiXi |
|
15 20 25 30 35 40 |
8 7 P 14 15 6 |
120 140 25p 420 525 240 |
|
|
|
|
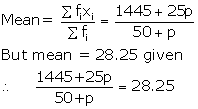
![]() 1445 + 25p = (28.25)(50+p)
1445 + 25p = (28.25)(50+p)
![]() 1445 + 25p = 1412.50 + 28.25p
1445 + 25p = 1412.50 + 28.25p
![]() -28.25p + 25p = -1445 + 1412.50
-28.25p + 25p = -1445 + 1412.50
![]() -3.25p = -32.5
-3.25p = -32.5
![]()
![]()
![]() the value of p=10
the value of p=10
Solution 10
We prepare the following frequency distribution table:
|
(Xi) |
(fi) |
fiXi |
|
8 12 15 P 20 25 30 |
12 16 20 24 16 8 4
|
96 192 300 24p 320 200 120
|
|
|
|
|
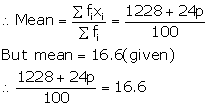
![]() 1228 + 24p = 1660
1228 + 24p = 1660
![]() 24p = 1660-1228
24p = 1660-1228
![]() 24p = 432
24p = 432
![]()
![]()
![]() the value of p =18
the value of p =18
Solution 11
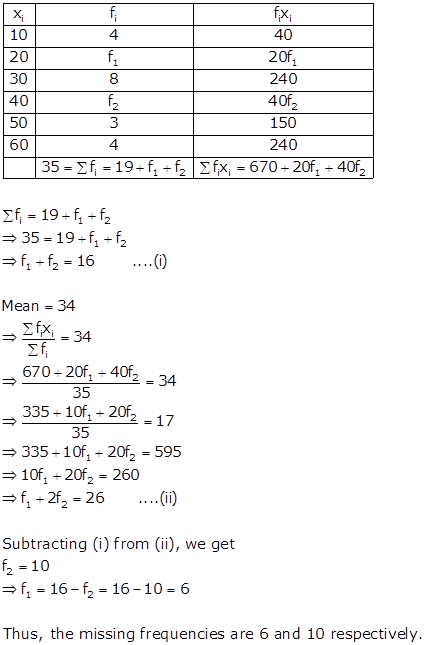
Solution 12
Let f1 and f2 be the missing frequencies.
We prepare the following frequency distribution table.
|
(Xi) |
(fi) |
fixi |
|
10 30 50 70 90
|
17 f1 32 f2 19
|
170 30f1 1600 70f2 1710 |
|
Total |
120 |
3480 + 30f1 + 70f2 |
Here,
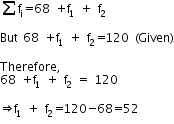
Thus, ![]() .......(1)
.......(1)
Also,

Substituting the value of f1 in equation 1, we have,
f2=52 - 28 = 24
Thus, the missing frequencies are f1 =28 and f2=24 respectively.
Solution 13
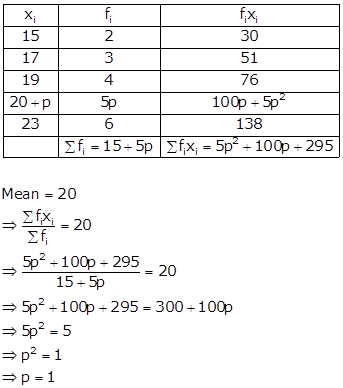
Solution 14