Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 17 - Bar Graph, Histogram and Frequency Polygon
Bar Graph, Histogram and Frequency Polygon Exercise Ex. 17A
Solution 1
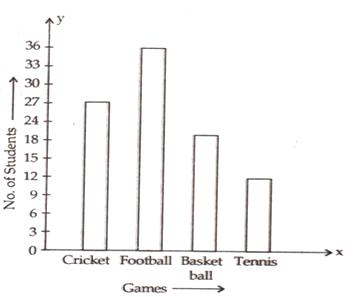
Take the various types of games along the x-axis and the number of students along the y-axis.
Along the y-axis, take 1 small square=3 units.
All the bars should be of same width and same space should be left between the consecutive bars.
Now we shall draw the bar chart, as shown below:
Solution 2
Take the timings along the x-axis and the temperatures along the y-axis.
Along the y-axis, take 1 small square=5 units.
All the bars should be of same width and same space should be left between the consecutive bars.
Now we shall draw the bar chart, as shown below:
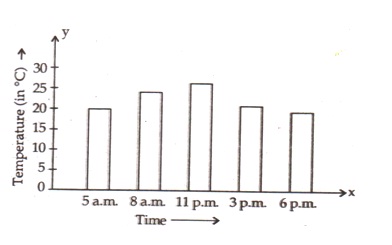
Solution 3
Solution 4
Take the various types of sports along the x-axis and the number of students along the y-axis.
Along the y-axis, take 1 small square=10 units.
All the bars should be of same width and same space should be left between the consecutive bars.
Now we shall draw the bar chart, as shown below:
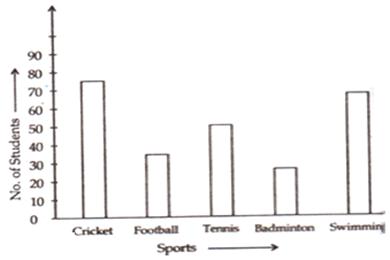
Solution 5
Take the academic year along the x-axis and the number of students along the y-axis.
Along the y-axis, take 1 big division =200 units.
All the bars should be of same width and same space should be left between the consecutive bars.
Now we shall draw the bar chart, as shown below:
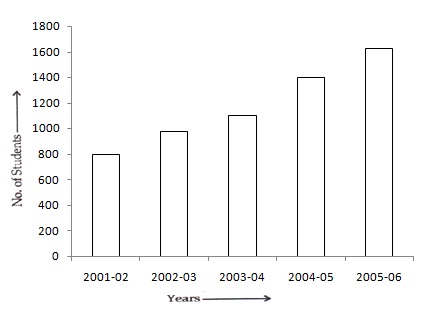
Solution 6
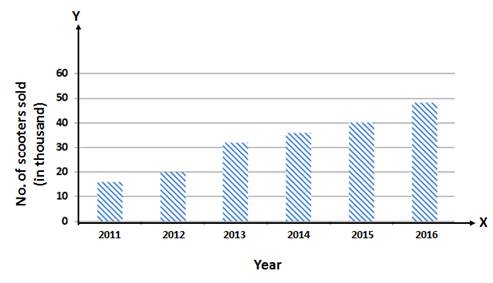
Solution 7
Take city along the x-axis and distance from Delhi (in Km) along the y-axis.
Along the y-axis, take 1 big division =200 units.
All the bars should be of same width and same space should be left between the consecutive bars.
Now we shall draw the bar chart, as shown below:
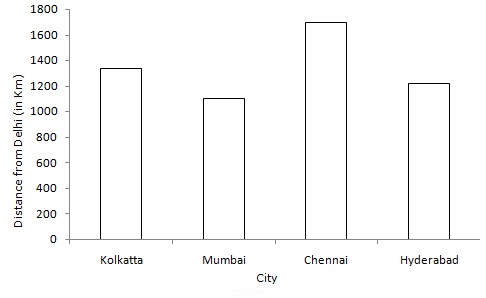
Solution 8
Take the countries along the x-axis and the birth rate (per thousand) along the y-axis.
Along the y-axis, take 1 big division = 5 units.
All the bars should be of same width and same space should be left between the consecutive bars.
Now we shall draw the bar chart, as shown below:

Solution 9
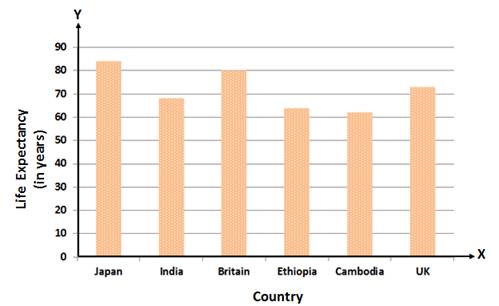
Solution 10

Solution 11
Take themode of transport along the x-axis and the number of students along the y-axis.
Along the y-axis, take 1 big division = 100 units.
All the bars should be of same width and same space should be left between the consecutive bars.
Now we shall draw the bar chart, as shown below:
Solution 12
(i) The bar graph shows the marks obtained by a student in various subject in an examination.
(ii) The student is very good in mathematics.
(iii) He is poor in Hindi
(iv) Average marks =![]()
Bar Graph, Histogram and Frequency Polygon Exercise Ex. 17B
Solution 1
Given frequency distribution is as below :
|
Daily wages (in Rs) |
340-380 |
380-420 |
420-460 |
460-500 |
500-540 |
540-580 |
|
No. of workers |
16 |
9 |
12 |
2 |
7 |
4 |
In the class intervals, if the upper limit of one class is the lower limit of the next class, it is known as the exclusive method of classification.
Clearly, the given frequency distribution is in the exclusive form.
To draw the required histogram , take class intervals , i.e. daily wages (in Rs. ) along x-axis and frequencies i.e.no.of workers alongy-axisand draw rectangles . So , we get the requiredhistogram .
Since the scale on X-axis starts at 340, a kink(break) is indicated near the origin to show that the graph is drawn to scale beginning at 340.
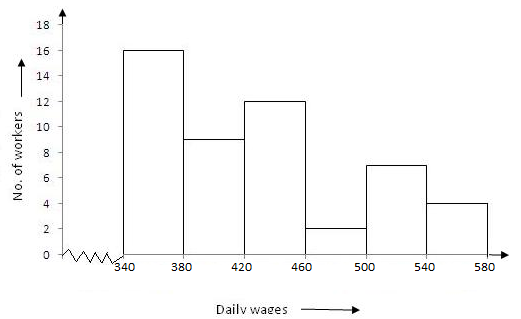
Solution 2
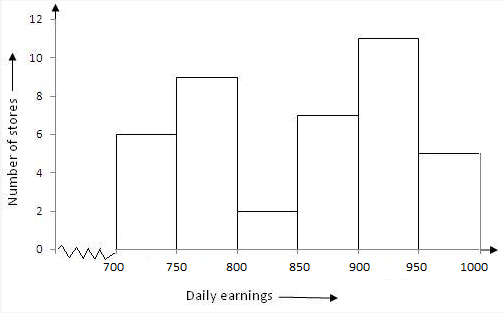
Given frequency distribution is as below :
|
Daily earnings (in Rs) |
700-750 |
750-800 |
800-850 |
850-900 |
900-950 |
950-1000 |
|
No of stores |
6 |
9 |
2 |
7 |
11 |
5 |
In the class intervals, if the upper limit of one class is the lower limit of the next class, it is known as the exclusive method of classification.
Clearly, the given frequency distribution is in the exclusive form.
We take class intervals, i.e. daily earnings (in Rs .) along x-axis and frequencies i.e. number of stores along y-axis. So , we get the required histogram .
Since the scale on X-axis starts at 700, a kink(break) is indicated near the origin to show that the graph is drawn to scale beginning at 700.
Solution 3
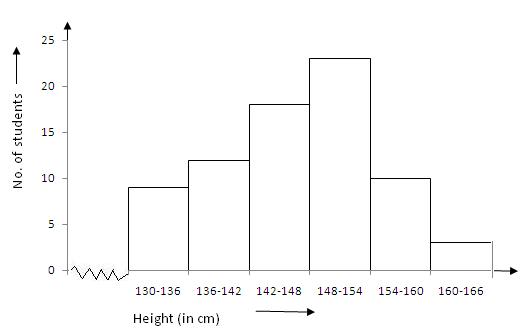
|
Height (in cm) |
130-136 |
136-142 |
142-148 |
148-154 |
154-160 |
160-166 |
|
No. of students |
9 |
12 |
18 |
23 |
10 |
3 |
In the class intervals, if the upper limit of one class is the lower limit of the next class, it is known as the exclusive method of classification.
Clearly, the given frequency distribution is in the exclusive form.
We take class intervals, i.e. height (in cm ) along x-axis and frequencies i.e. number of student s along y-axis . So we get the required histogram.
Since the scale on X-axis starts at 130, a kink(break) is indicated near the origin to show that the graph is drawn to scale beginning at 130.
Solution 4
(i) Histogram is as follows:
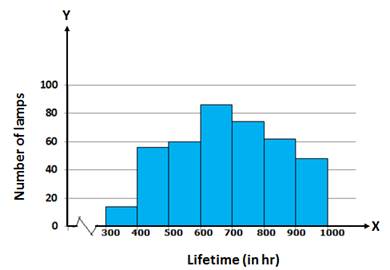
(ii) Number of lamps having lifetime more than 700 hours = 74 + 62 + 48 = 184
Solution 5
Give frequency distribution is as below :
|
Class interval |
8-13 |
13-18 |
18-23 |
23-28 |
28-33 |
33-38 |
38-43 |
|
Frequency |
320 |
780 |
160 |
540 |
260 |
100 |
80 |
In the class intervals, if the upper limit of one class is the lower limit of the next class, it is known as the exclusive method of classification.
Clearly, the given frequency distribution is in the exclusive form.
We take class intervals along x-axis and frequency along y-axis . So , we get the required histogram.
Since the scale on X-axis starts at 8, a kink(break) is indicated near the origin to show that the graph is drawn to scale beginning at 8.
Solution 6
Histogram is the graphical representation of a frequency distribution in the form of rectangles, such that there is no gap between any two successive rectangles.
Clearly the given frequency distribution is in inclusive form, that is there is a gap between the upper limit of a class and the lower limit of the next class.
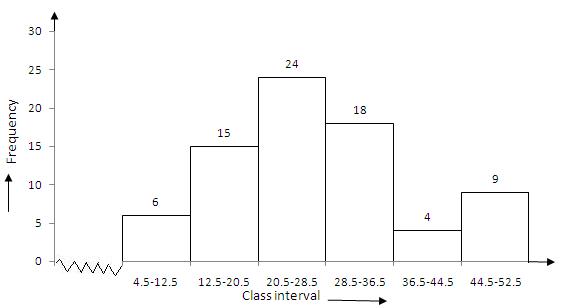
Therefore, we need to convert the given frequency distribution into exclusive form, as shown below:
|
Class interval |
4.5-12.5 |
12.5-20.5 |
20.5-28.5 |
28.5-36.5 |
36.5-44.5 |
44.5-52.5 |
|
Frequency |
6 |
15 |
24 |
18 |
4 |
9 |
To draw the required histogram , take class intervals, along x-axis and frequencies along y-axis and draw rectangles . So, we get the required histogram .
Since the scale on X-axis starts at 4.5, a kink(break) is indicated near the origin to show that the graph is drawn to scale beginning at 4.5.
Solution 7
Given frequency distribution is as below :
|
Age group (in years ) |
10-16 |
17-23 |
24-30 |
31-37 |
38-44 |
45-51 |
52-58 |
|
No. of illiterate persons |
175 |
325 |
100 |
150 |
250 |
400 |
525 |
Histogram is the graphical representation of a frequency distribution in the form of rectangles, such that there is no gap between any two successive rectangles.
Clearly the given frequency distribution is in inclusive form, that is there is a gap between the upper limit of a class and the lower limit of the next class.
Therefore, we need to convert the frequency distribution in exclusive form, as shown below:
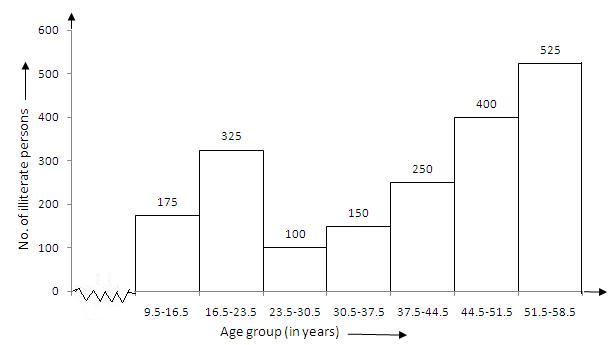
|
Age group(in years) |
9.5-16.5 |
16.5-23.5 |
23.5-30.5 |
30.5-37.5 |
37.5-44.4 |
44.5-51.5 |
51.5-58.5 |
|
No of illiterate persons |
175 |
325 |
100 |
150 |
250 |
400 |
525 |
To draw the required histogram , take class intervals, that is age group, along x-axis and frequencies, that is number of illiterate persons along y-axis and draw rectangles . So , we get the required histogram.
Since the scale on X-axis starts at 9.5, a kink(break) is indicated near the origin to show that the graph is drawn to scale beginning at 9.5.
Solution 8
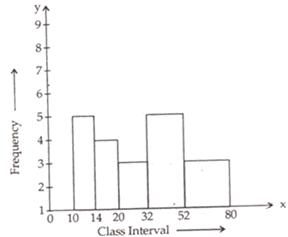
given frequency distribution is as below :
|
Class interval |
10-14 |
14-20 |
20-32 |
32-52 |
52-80 |
|
Frequency |
5 |
6 |
9 |
25 |
21 |
In the above table , class intervals are of unequal size, so we calculate the adjusted frequency by using the following formula :

Thus , the adjusted frequency table is
|
Class intervals |
frequency |
Adjusted Frequency |
|
10-14
14-20
20-32
32-52
52-80 |
5
6
9
25
21 |
|
Now take class intervals along x-axis and adjusted frequency along y-axis and constant rectangles having their bases as class size and heights as the corresponding adjusted frequencies.
Thus, we obtain the histogram as shown below:
Solution 9
(i) Minimum class size = 6 - 4 = 2
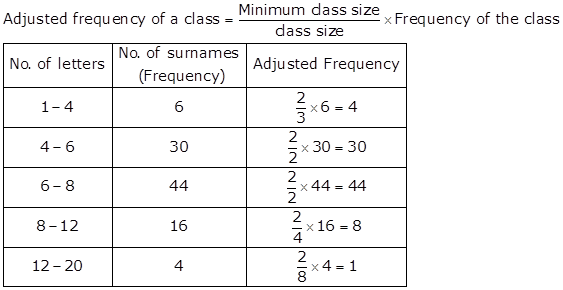
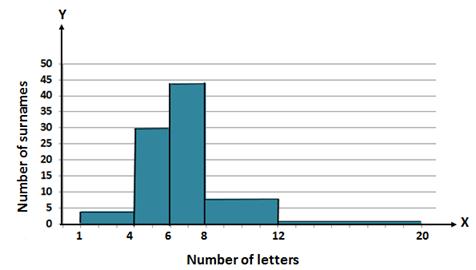
(ii) Maximum number of surnames lies in the class interval 6 - 8.
Solution 10
Minimum class size = 10 - 5 = 5
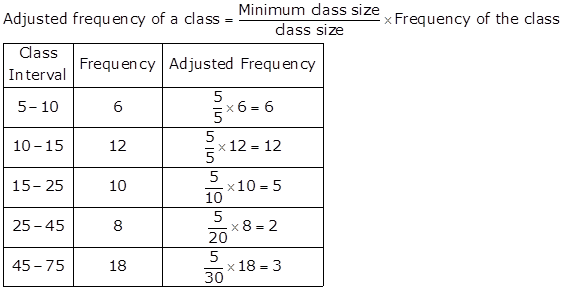

Solution 11
Minimum class size = 50 - 45 = 5
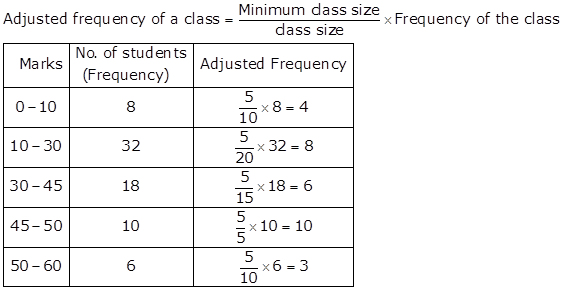
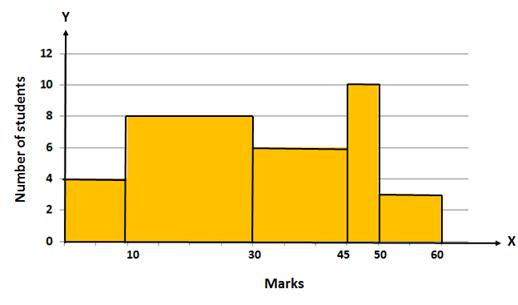
Solution 12
The given frequency distribution is as below:
|
Age in years |
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
60-70 |
|
No of patients |
2 |
5 |
12 |
19 |
9 |
4 |
In order to draw, frequency polygon, we require class marks.
The class mark of a class interval is: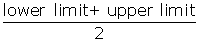
The frequency distribution table with class marks is given below:
|
Class- intervals |
Class marks |
Frequency |
|
0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 |
5 15 25 35 45 55 65 75 |
0 2 5 12 19 9 4 0 |
In the above table, we have taken imaginary class intervals 0-10 at beginning and 70-80 at the end, each with frequency zero . Now take class marks along x-axis and the corresponding frequencies along y-axis.
Plot points (5,0), (15,2), (25, 5), (35, 12), (45, 19), (55, 9), (65, 4) and (75, 0) and draw line segments.
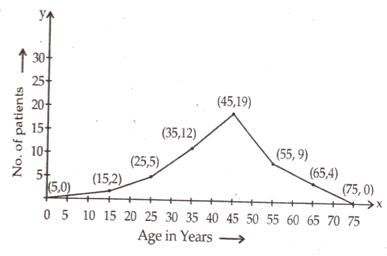
Solution 13
The given frequency distribution table is as below:
|
Class intervals |
1-10 |
11-20 |
21-30 |
31-40 |
41-50 |
51-60 |
|
Frequency |
8 |
3 |
6 |
12 |
2 |
7 |
This table has inclusive class intervals and so these are to be converted into exclusive class intervals (i.e true class limits).
These are (0.5-10.5), (10.5-20.5), (20.5-30.5), (30.5-40.5),
(40.5-50.5), and (50.5-60.5)
In order to draw a frequency polygon, we need to determine the class marks. Class marks of a class interval =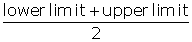
Take imaginary class interval ( -9.5-0.5) at the beginning and (60.5-70.5) at the end , each with frequency zero. So we have the following table
|
Class intervals |
True class intervals |
Class marks |
Frequency |
|
(-9)-0 1-10 11-20 21-30 31-40 41-50 51-60 61-70
|
(-9.5)-0.5 0.5-10.5 10.5-20.5 20.5-30.5 30.5-40.5 40.5-50.5 50.5-60.5 60.5-70.5 |
-4.5 5.5 15.5 25.5 35.5 45.5 55.5 65.5 |
0 8 3 6 12 2 7 0 |
Now, take class marks along x-axis and their corresponding frequencies along y-axis.
Mark the points and join them.
Thus, we obtain a complete frequency polygon as shown below:
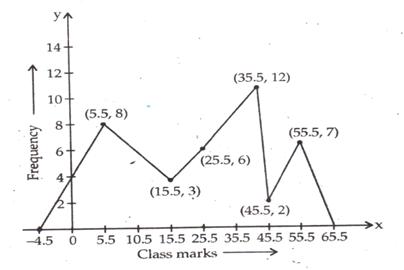
Solution 14
The given frequency distribution is as under
|
Age in years |
10-20 |
20-30 |
30-40 |
40-50 |
50-60 |
60-70 |
|
Numbers of patients |
90 |
40 |
60 |
20 |
120 |
30 |
Take class intervals i.e age in years along x-axis and number of patients of width equal to the size of the class intervals and height equal to the corresponding frequencies.
Thus we get the required histogram.
In order to draw frequency polygon,we take imaginary intervals 0-10 at the beginning and 70-80 at the end each with frequency zero and join the mid-points of top of the rectangles.
Thus, we obtain a complete frequency polygon, shown below:
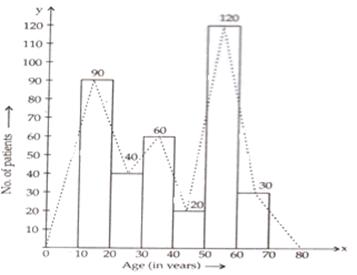
Solution 15
The given frequency distribution is as below :
|
Class intervals |
20-25 |
25-30 |
30-35 |
35-40 |
40-45 |
45-50 |
|
Frequency |
30 |
24 |
52 |
28 |
46 |
10 |
Take class intervals along x-axis and frequencies along y-axis and draw rectangle s of width equal to the size of the class intervals and heights equal to the corresponding frequencies.
Thus we get required histogram.
Now take imaginary class intervals 15-20 at the beginning and 50-55 at the end , each with frequency zero and join the mid points of top of the rectangles to get the required frequency polygon.

Solution 16
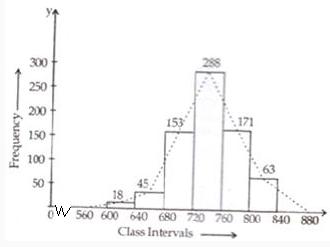
The given frequency distribution table is given below :
|
Class interval |
600-640 |
640-680 |
680-720 |
720-760 |
760-800 |
800-840 |
|
Frequency |
18 |
45 |
153 |
288 |
171 |
63 |
Take class intervals along x-axis and frequencies along y-axis and draw rectangles of width equal to to size of class intervals and height equal to their corresponding frequencies.
Thus we get the requiredhistogram.
Take imaginary class intervals 560-600 at the beginning and 840-880 at the end, each with frequency zero.
Now join the mid points of the top of the rectangles to get the required frequency polygon.