Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 14 - Areas of Triangles and Quadrilaterals
Areas of Triangles and Quadrilaterals Exercise MCQ
Solution 1
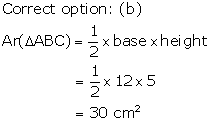
Solution 2
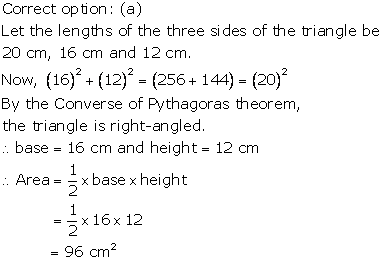
Solution 3

Solution 4

Solution 5
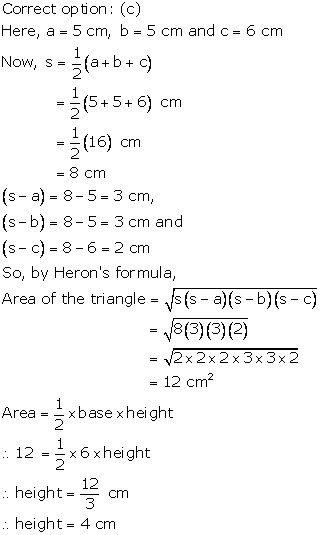
Solution 6

Solution 7
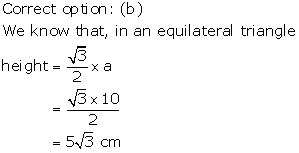
Solution 8

Solution 9

Solution 10

Solution 11

Solution 12


Solution 13

Solution 14

Solution 15

Solution 16

Areas of Triangles and Quadrilaterals Exercise Ex. 14
Solution 1
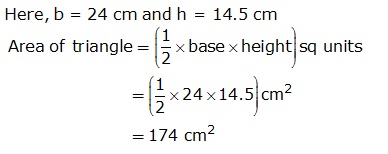
Solution 2

Solution 3

Solution 4

Solution 5

Solution 6
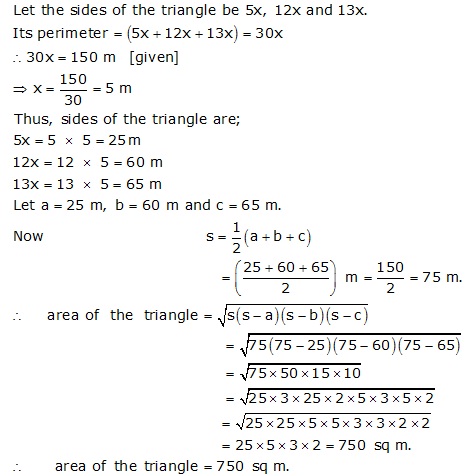
Solution 7
It is given that the sides a, b, c of the triangle are in the ratio 25 : 17 : 12,
i.e. a : b : c = 25 : 17 : 12
⇒ a = 25x, b = 17x and c = 12x
Given, perimeter = 540 m
⇒ 25x + 17x + 12x = 540
⇒ 54x = 540
⇒ x = 10
So, the sides of the triangle are
a = 25x = 25(10) = 250 m
b = 17x = 17(10) = 170 m
c = 12x = 12(10) = 120 m
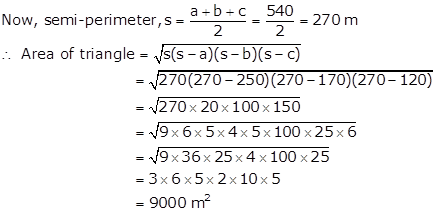
Cost of ploughing the field = Rs. 5/m2
⇒ Cost of ploughing 9000 m2 = Rs. (5 × 9000) = Rs. 45,000
Solution 8
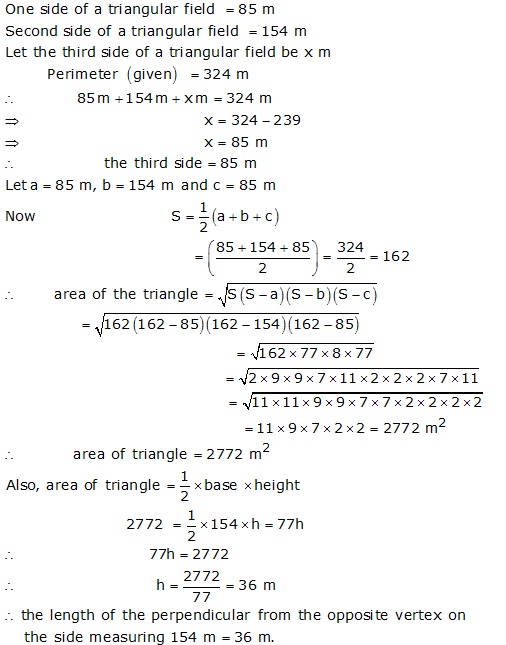
Solution 9
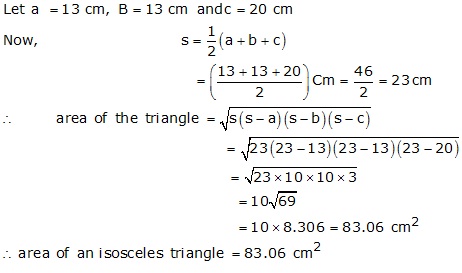
Solution 10

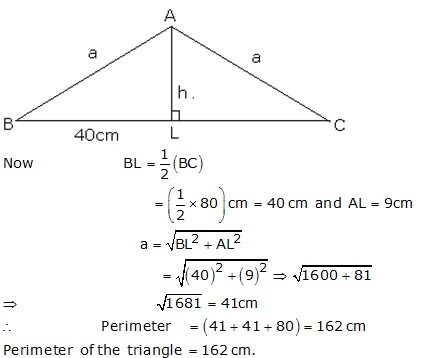
Solution 11
It is given that the ratio of equal side to its base is 3 : 2.
⇒ Ratio of sides of isosceles triangle = 3 : 3 : 2
i.e. a : b : c = 3 : 3 : 2
⇒ a = 3x, b = 3x and c = 2x
Given, perimeter = 32 cm
⇒ 3x + 3x + 2x = 32
⇒ 8x = 32
⇒ x = 4
So, the sides of the triangle are
a = 3x = 3(4) = 12 cm
b = 3x = 3(4) = 12 cm
c = 2x = 2(4) = 8 cm
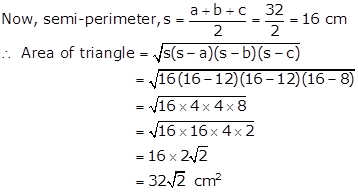
Solution 12
Let the three sides of a triangle be a, b and c respectively such that c is the smallest side.
Then, we have
a = c + 4
And, b = 2c - 6
Given, perimeter = 50 cm
⇒ a + b + c = 50
⇒ (c + 4) + (2c - 6) + c = 50
⇒ 4c - 2 = 50
⇒ 4c = 52
⇒ c = 13
So, the sides of the triangle are
a = c + 4 = 13 + 4 = 17 cm
b = 2c - 6 = 2(13) - 6 = 20 cm
c = 13 cm

Solution 13
Three sides of a wall are 13 m, 14 m and 15 m respectively.
i.e.
a = 13 m, b = 14 m and c = 15 m
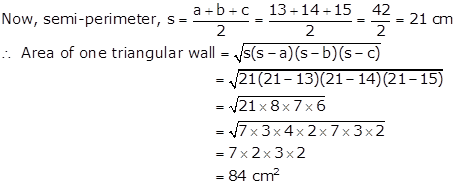
Rent for a year = Rs. 2000/m2
⇒ Rent for 6 months = Rs. 1000/m2
Thus, total rent paid for 6 months = Rs. (1000 × 84) = Rs. 84,000
Solution 14

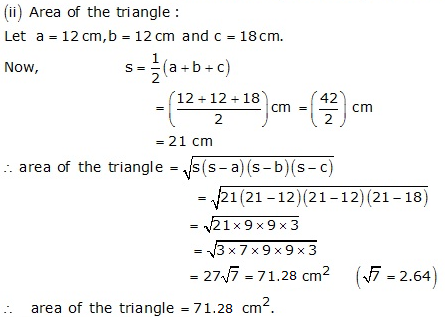

Solution 15

Solution 16

Solution 17
(i) Area of an equilateral
triangle=![]()
Where a is the side of the equilateral triangle

Solution 18

Solution 19

Solution 20
In right triangle ADB, by Pythagoras theorem,
AB2 = AD2 + BD2 = 122 + 162 = 144 + 256 = 400
⇒ AB = 20 cm
![]()
For ΔABC,
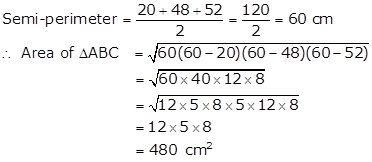
Thus, area of shaded region
= Area of ΔABC - Area of ΔABD
= (480 - 96) cm2
= 384 cm2
Solution 21

Let ABCD be the given quadrilateral such that ∠ABC = 90° and AB = 6 cm, BC = 8 cm, CD = 12 cm and AD = 14 cm.
In ΔABC, by Pythagoras theorem,
AC2 = AB2 + BC2 = 62 + 82 = 36 + 64 = 100
⇒ AC = 10 cm
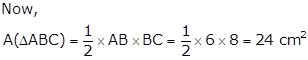
In ΔACD, AC = 10 cm, CD = 12 cm and AD = 14 cm
Let a = 10 cm, b = 12 cm and c = 14 cm

Thus, area of quadrilateral ABCD
= A(ΔABC) + A(ΔACD)
= (24 + 58.8) cm2
= 82.8 cm2
Solution 22
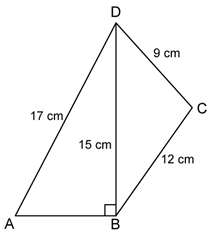
In ΔABD, by Pythagoras theorem,
AB2 = AD2 - BD2 = 172 - 152 = 289 - 225 = 64
⇒ AB = 8 cm
∴ Perimeter of quadrilateral ABCD = AB + BC + CD + AD
= 8 + 12 + 9 + 17
= 46 cm
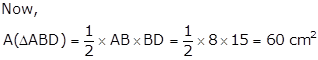
In ΔBCD, BC = 12 cm, CD = 9 cm and BD = 15 cm
Let a = 12 cm, b = 9 cm and c = 15 cm

Thus, area of quadrilateral ABCD
= A(ΔABD) + A(ΔBCD)
= (60 + 54) cm2
= 114 cm2
Solution 23
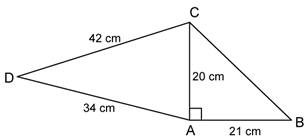
In ΔBAC, by Pythagoras theorem,
BC2 = AC2 + AB2 = 202 + 212 = 400 + 441 = 841
⇒ BC = 29 cm
∴ Perimeter of quadrilateral ABCD = AB + BC + CD + AD
= 21 + 29 + 42 + 34
= 126 cm
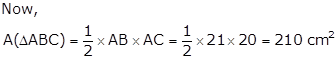
In ΔACD, AC = 20 cm, CD = 42 cm and AD = 34 cm
Let a = 20 cm, b = 42 cm and c = 34 cm
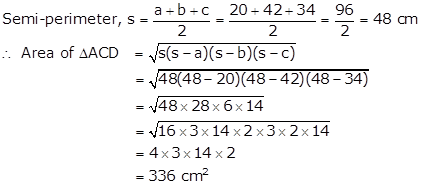
Thus, area of quadrilateral ABCD
= A(ΔABC) + A(ΔACD)
= (210 + 336) cm2
= 546 cm2
Solution 24
Perimeter of quad. ABCD = AB + BC + CD + DA = 10 + 26 + 26 + 24 = 86 cm
Solution 25
Solution 26
Solution 27
Solution 28
Let the smaller parallel side of trapezium = x cm
Then, larger parallel side = (x + 4) cm
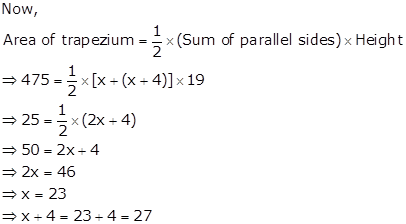
Thus, the lengths of two parallel sides are 23 cm and 27 cm respectively.
Solution 29
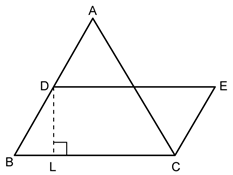
In ΔABC, AB = 7.5 cm, BC = 7 cm and AC = 6.5 cm
Let a = 7.5 cm, b = 7 cm and c = 6.5 cm
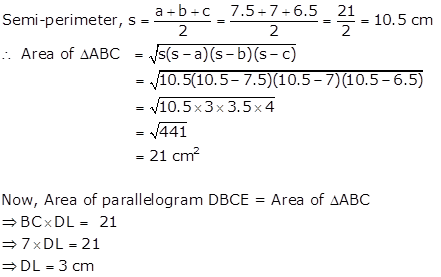
Solution 30
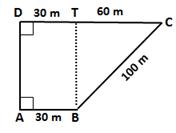
Construction: Draw BT ⊥ CD
In ΔBTC, by Pythagoras theorem,
BT2 = BC2 - CT2 = 1002 - 602 = 10000 - 3600 = 6400
⇒ BT = 80 m
⇒ AD = BT = 80 m
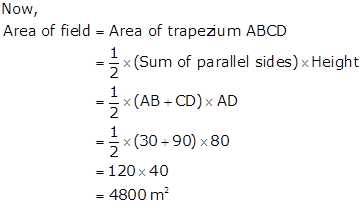
Cost of ploughing 1 m2 field = Rs. 5
⇒ Cost of ploughing 4800 m2 field = Rs. (5 × 4800) = Rs. 24,000
Solution 31
Length of rectangular plot = 40 m
Width of rectangular plot = 15 m
Keeping 3 m wide space in the front and back,
length of rectangular plot = 40 - 3 - 3 = 34 m
Keeping 2 m wide space on both the sides,
width of rectangular plot = 15 - 2 - 2 = 11 m
Thus, largest area where house can be constructed
= 34 m × 11 m
= 374 m2
Solution 32
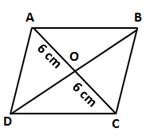
Let ABCD be the rhombus-shaped sheet.
Perimeter = 40 cm
⇒ 4 × Side = 40 cm
⇒ Side = 10 cm
⇒ AB = BC = CD = AD = 10 cm
Let diagonal AC = 12 cm
Since diagonals of a rhombus bisect each other at right angles,
AO = OC = 6 cm
In right ΔAOD, by Pythagoras theorem,
OD2 = AD2 - AO2 = 102 - 62 = 100 - 36 = 64
⇒ OD = 8 cm
⇒ BD = 2 × OD = 2 × 8 = 16 cm
Now,

Cost of painting = Rs. 5/cm2
∴ Cost of painting rhombus on both sides = Rs. 5 × (96 + 96)
= Rs. 5 × 192
= Rs. 960
Solution 33
Let the sides of a triangle be a, b, c respectively and 's' be its semi-perimeter.
Then, we have
s - a = 8 cm
s - b = 7 cm
s - c = 5 cm
Now, (s - a) + (s - b) + (s - c) = 8 + 7 + 5
⇒ 3s - (a + b + c) = 20
⇒ 3s - 2s = 20
⇒ s = 20
Thus, we have
a = s - 8 = 20 - 8 = 12 cm
b = s - 7 = 20 - 7 = 13 cm
c = s - 5 = 20 - 5 = 15 cm

Solution 34

Solution 35

Solution 36
 In ΔAEF, AE = 20
cm, EF = 14 cm and AF = 20 cm
In ΔAEF, AE = 20
cm, EF = 14 cm and AF = 20 cm
Let a = 20 cm, b = 14 cm and c = 20 cm
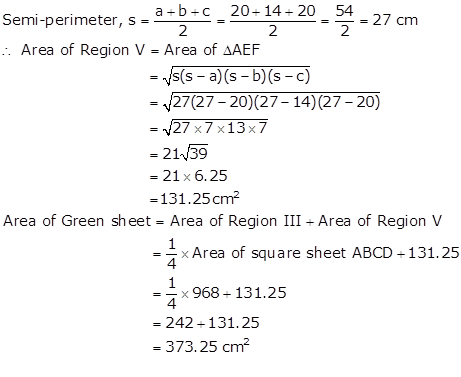
Solution 37
For road ABCD, i.e. for rectangle ABCD,
Length = 75 m
Breadth = 4 m
Area of road ABCD = Length × Breadth = 75 m × 4m = 300 m2
For road PQRS, i.e. for rectangle PQRS,
Length = 60 m
Breadth = 4 m
Area of road PQRS = Length × Breadth = 60 m × 4 m = 240 m2
For road EFGH, i.e. for square EFGH,
Side = 4 m
Area of road EFGH = (Side)2 = (4)2 = 16 m2
Total area of road for gravelling
= Area of road ABCD + Area of road PQRS - Area of road EFGH
= 300 + 240 - 16
= 524 m2
Cost of gravelling the road = Rs. 50 per m2
∴ Cost of gravelling 524 m2 road = Rs. (50 × 524) = Rs. 26,200
Solution 38
Area of cross section = Area of trapezium = 640 m2
Length of top + Length of bottom
= sum of parallel sides
= 10 m + 6 m
= 16 m
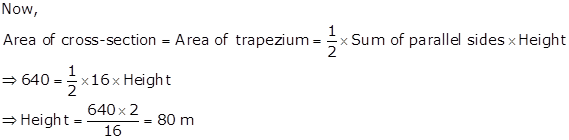 Thus, the depth of the canal is 80 m.
Thus, the depth of the canal is 80 m.
Solution 39
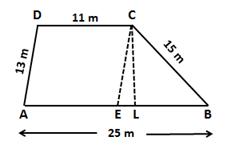
From C, draw CE ∥ DA.
Clearly, ADCE is a parallelogram having AD ∥ EC and AE ∥ DC such that AD = 13 m and D = 11 m.
AE = DC = 11 m and EC = AD = 13 m
⇒ BE = AB - AE = 25 - 11 = 14 m
Thus, in ΔBCE, we have
BC = 15 m, CE = 13 m and BE = 14 m
Let a = 15 m, b = 13 m and c = 14 m
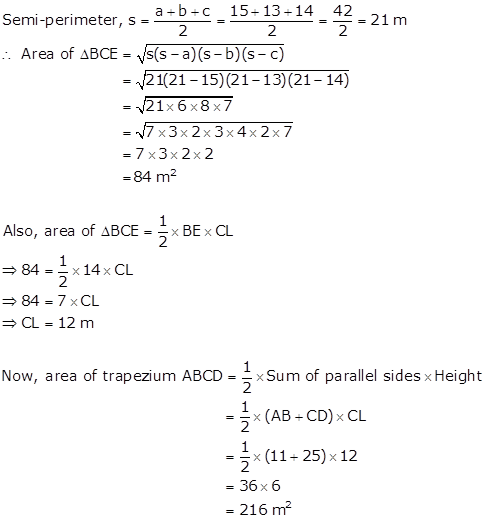
Solution 40
Let the smaller parallel side = x cm
Then, longer parallel side = (x + 8) cm
Height = 24 cm
Area of trapezium = 312 cm2
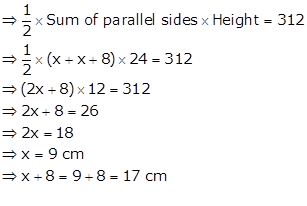
Thus, the lengths of parallel sides are 9 cm and 17 cm respectively.
Solution 41
Area of parallelogram = Area of rhombus
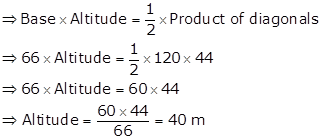
Solution 42
Area of parallelogram = Area of square
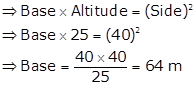
Solution 43
Let ABCD be a rhombus and let diagonals AC and BD intersect each other at point O.
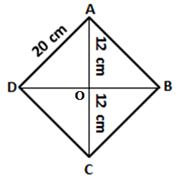
We know that diagonals of a rhombus bisect each other at right angles.
Thus, in right-angled ΔAOD, by Pythagoras theorem,
OD2 = AD2 - OA2 = 202 - 122 = 400 - 144 = 256
⇒ OD = 16 cm
⇒ BD = 2(OD) = 2(16) = 32 cm
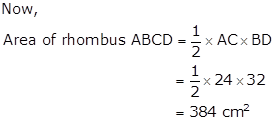
Solution 44
(i) Area of a rhombus = 480 cm2
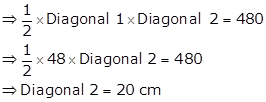
(ii) Let diagonal AC = 48 cm and diagonal BD = 20 cm
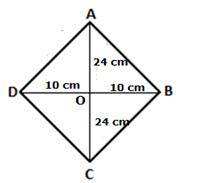
We know that diagonals of a rhombus bisect each other at right angles.
Thus, in right-angled ΔAOD, by Pythagoras theorem,
AD2 = OA2 + OD2 = 242 + 102 = 576 + 100 = 676
⇒ AD = 26 cm
⇒ AD = BC = CD = AD = 26 cm
Thus, the length of each side of rhombus is 26 cm.
(iii) Perimeter of a rhombus = 4 × side = 4 × 26 = 104 cm





