Class 9 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 11 - Areas of Parallelograms and Triangles
Areas of Parallelograms and Triangles Exercise MCQ
Solution 1

Solution 2
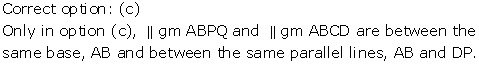
Solution 3
![]()
Solution 4

Solution 5

Solution 6
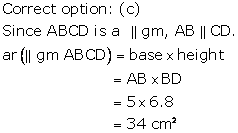
Solution 7

Solution 8

Solution 9
Correct option: (c)
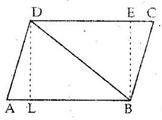
Area of ∥gm ABCD = Base × Height = DC × DL
Solution 10
Correct option: (b)
Parallelograms on equal bases and between the same parallels are equal in area.
Solution 11
Correct option: (a)
ΔBMP and parallelogram ABPQ are on the same base BP and between the same parallels AQ and BP.
![]()
Parallelograms ABPQ and ABCD are on the same base AB and between the same parallels AB and PD.

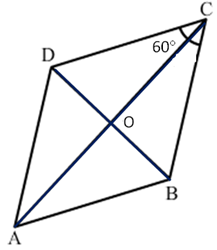
Solution 12
Correct option: (a)
ΔABC is divided into four triangles of equal area.
A(parallelogram AFDE) = A(ΔAFE) + A(DFE)
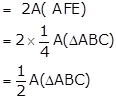
Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18
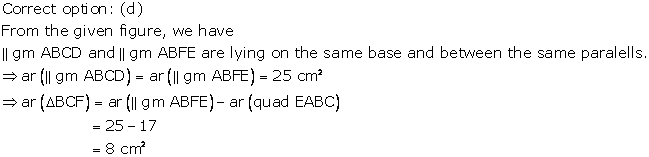
Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27
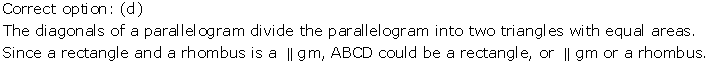
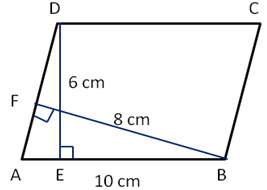
Solution 28

Solution 29
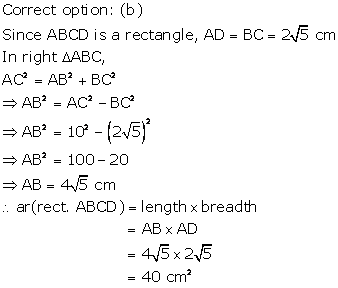
Solution 30

Solution 31

Solution 32


Solution 33
![]()

Solution 34

Solution 35
Solution 36

Solution 37

Areas of Parallelograms and Triangles Exercise Ex. 11A
Solution 2
![]()


Solution 3
![]()


Solution 5

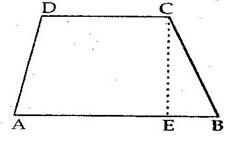
Solution 6(ii)
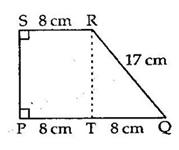

Solution 6(i)
![]()
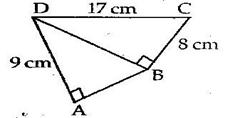

Solution 8

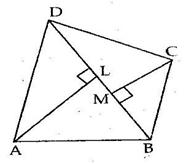

Solution 10
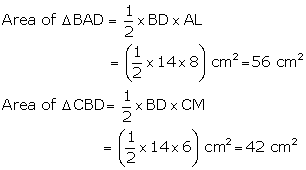
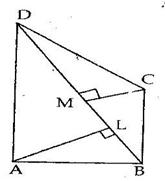
![]()
Solution 13
Solution 14
Solution 15
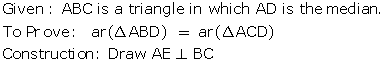
Solution 16
Solution 20
![]()
![]()

Solution 21
![]()


Solution 22
![]()

Solution 24


Solution 25
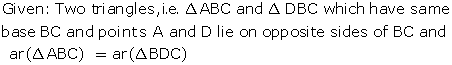
Solution 28
![]()
Solution 30
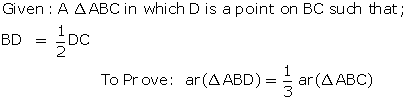
Solution 32
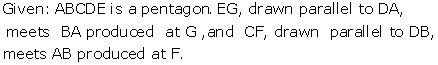

Solution 34
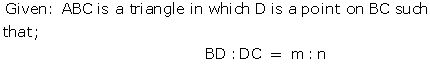


Areas of Parallelograms and Triangles Exercise Ex. 11
Solution 1
Following figures lie on the same base and between the same parallels:
Figure (i): No
Figure (ii): No
Figure (iii): Yes, common base - AB, parallel lines - AB and DE
Figure (iv): No
Figure (v): Yes, common base - BC, parallel lines - BC and AD
Figure (vi): Yes, common base - CD, parallel lines - CD and BP
Solution 4
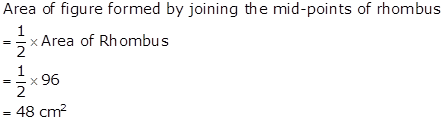
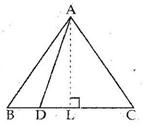
Solution 7
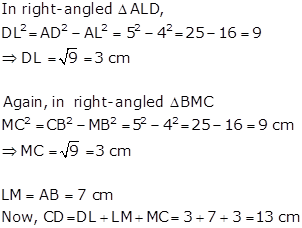

Solution 9
Construction: Join AC
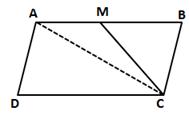
Diagonal AC divides the parallelogram ABCD into two triangles of equal area.
⇒ A(ΔADC) = A(ΔABC) ….(i)
ΔADC and parallelogram ABCD are on the same base CD and between the same parallel lines DC and AM.
![]()
Since M is the mid-point of AB,
![]()
A(AMCD) = A(ΔADC) + A(ΔAMC)
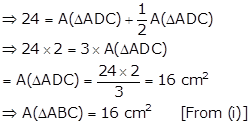
Solution 11
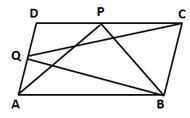
Since ΔAPB and parallelogram ABCD are on the same base AB and between the same parallels AB and DC, we have
![]()
Similarly, ΔBQC and parallelogram ABCD are on the same base BC and between the same parallels BC and AD, we have
![]()
From (i) and (ii),
A(ΔAPB) = A(ΔBQC)
Solution 12
(i) Parallelograms MNPQ and ABPQ are on the same base PQ and between the same parallels PQ and MB.
![]()
(ii) ΔATQ and parallelogram ABPQ are on the same base AQ and between the same parallels AQ and BP.

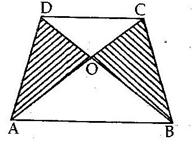
Solution 17
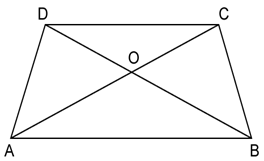
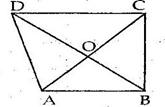
We know that median of a triangle divides it into two triangles of equal area.
Now, AO is the median of ΔACD.
⇒ A(ΔCOA) = A(ΔDOA) ….(i)
And, BO is the median of ΔBCD.
⇒ A(ΔCOB) = A(ΔDOB) ….(ii)
Adding (i) and (ii), we get
A(ΔCOA) + A(ΔCOB) = A(ΔDOA) + A(ΔDOB)
⇒ A(ΔABC) = A(ΔABD)
Solution 18
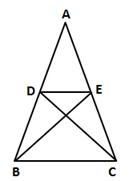
Since ΔBCD and ΔBCE are equal in area and have a same base BC.
Therefore,
Altitude from D of ΔBCD = Altitude from E of ΔBCE
⇒ ΔBCD and ΔBCE are between the same parallel lines.
⇒ DE ∥ BC
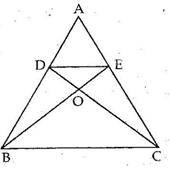
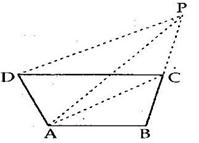
Solution 19
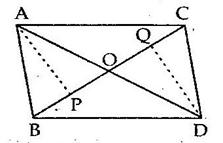
Construction: Join BD.
Let the diagonals AC and BD intersect at point O.
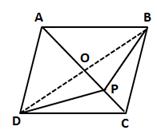
Diagonals of a parallelogram bisect each other.
Hence, O is the mid-point of both AC and BD.
We know that the median of a triangle divides it into two triangles of equal area.
In ΔABD, OA is the median.
⇒ A(ΔAOD) = A(ΔAOB) ….(i)
In ΔBPD, OP is the median.
⇒ A(ΔOPD) = A(ΔOPB) ….(ii)
Adding (i) and (ii), we get
A(ΔAOD) + A(ΔOPD) = A(ΔAOB) + A(ΔOPB)
⇒ A(ΔADP) = A(ΔABP)
Solution 23
In ΔMCQ and ΔMPB,
∠QCM = ∠PBM (alternate angles)
CM = BM (M is the mid-point of BC)
∠CMQ = ∠PMB (vertically opposite angles)
∴ ΔMCQ ≅ ΔMPB
⇒ A(ΔMCQ) = A(ΔMPB)
Now,
A(ABCD) = A(APQD) + A(DMPB) - A(ΔMCQ)
⇒ A(ABCD) = A(APQD)
Solution 26
In ΔADM and ΔPCM,
∠ADM = ∠PCM (alternate angles)
AD = CP (AD = BC = CP)
∠AMD = ∠PMC (vertically opposite angles)
∴ ΔADM ≅ ΔPCM
⇒ A(ΔADM) = A(ΔPCM)
And, DM = CM (c.p.c.t.)
⇒ BM is the median of ΔBDC.
⇒ A(ΔDMB) = A(ΔCMB)
⇒ A(ΔBDC) = 2 × A(ΔDMB) = 2 × 7 = 14 cm2
Now,
A(parallelogram ABCD) = 2 × A(ΔBDC) = 2 × 14 = 28 cm2
Solution 27
Construction: Join AC and BM
Let h be the distance between AB and CD.
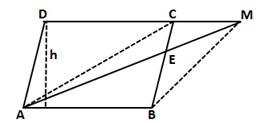
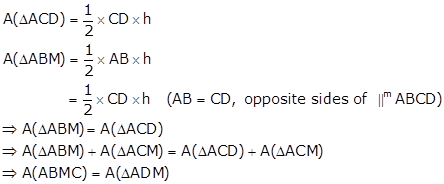
Solution 29
Construction: Join EF
Since the line segment joining the mid-points of two sides of a triangle is parallel to the third side,
FE ∥ BC
Clearly, ΔBEF and ΔCEF are on the same base EF and between the same parallel lines.
∴ A(ΔBEF) = A(ΔCEF)
⇒ A(ΔBEF) - A(ΔGEF) = A(ΔCEF) - A(ΔGEF)
⇒ A(ΔBFG) = A(ΔCEG) …(i)
We know that a median of a triangle divides it into two triangles of equal area.
⇒ A(ΔBEC) = A(ΔABE)
⇒ A(ΔBGC) + A(ΔCEG) = A(quad. AFGE) + A(ΔBFG)
⇒ A(ΔBGC) + A(ΔBFG) = A(quad. AFGE) + A(ΔBFG) [Using (i)]
⇒ A(A(ΔBGC) = A(quad. AFGE)
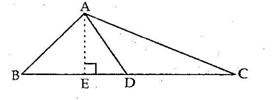
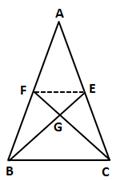
Solution 31

ΔDBC and ΔEBC are on the same base and between the same parallels.
⇒ A(ΔDBC) = A(ΔEBC) ….(i)
BE is the median of ΔABC.
Solution 33
ΔBCF and ΔACF are on the same base CF and between the same parallel lines CF and BA.
∴ A(ΔBCF) = A(ΔACF)
⇒ A(ΔBCF) - A(ΔCGF) = A(ΔACF) - A(ΔCGF)
⇒ A(ΔCBG) = A(ΔAFG)
Solution 35
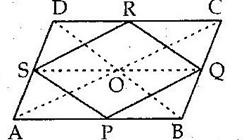
Construction: Join DB. Let DB cut MN at point Y.
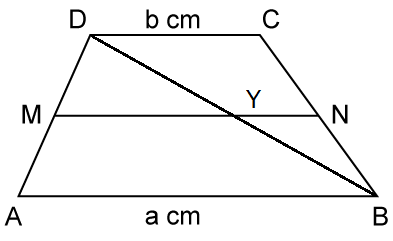
M and N are the mid-points of AD and BC respectively.
⇒ MN ∥ AB ∥ CD
In ΔADB, M is the mid-point of AD and MY ∥ AB.
∴ Y is the mid-point of DB.
![]()
Similarly, in ΔBDC,
![]()
Now, MN = MY + YN
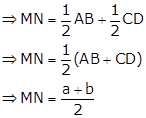
Construction: Draw DQ ⊥ AB. Let DQ cut MN at point P.
Then, P is the mid-point of DQ.
i.e. DP = PQ = h (say)
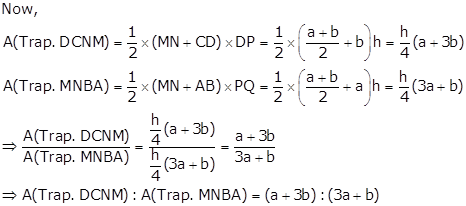
Solution 36
Construction: Join AC. Let AC cut EF at point Y.
E and F are the mid-points of AD and BC respectively.
⇒ EF ∥ AB ∥ CD
In ΔADC, E is the mid-point of AD and EY ∥ CD.
∴ Y is the mid-point of AC.
![]()
Similarly, in ΔABC,
![]()
Now, EF = EY + YF

Construction: Draw AQ ⊥ DC. Let AQ cut EF at point P.
Then, P is the mid-point of AQ.
i.e. AP = PQ = h (say)
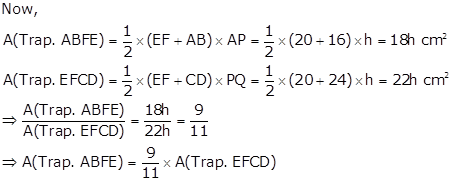
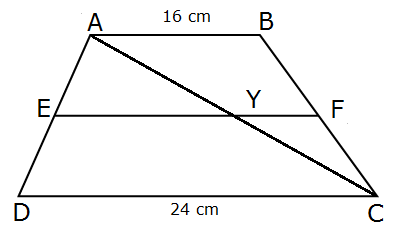
Solution 37
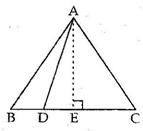
Since D and E are the mid-points of AB and AC respectively,
DE ∥ BC ∥ PQ
In ΔACP, AP ∥ DE and E is the mid-point of AC.
⇒ D is the mid-point of PC (converse of mid-point theorem)
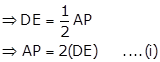
In ΔABQ, AQ ∥ DE and D is the mid-point of AB.
⇒ E is the mid-point of BQ (converse of mid-point theorem)
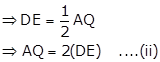
From (i) and (ii),
AP = AQ
Now, ΔACP and ΔABQ are on the equal bases AP and AQ and between the same parallels BC and PQ.
⇒ A(ΔACP) = A(ΔABQ)
Solution 38
In ΔRSC and ΔPQB,
∠CRS = ∠BPQ (RC ∥ PB, corresponding angles)
∠RSC = ∠PQB (RC ∥ PB, corresponding angles)
SC = QB (opposite sides of a parallelogram BQSC)
∴ ΔRSC ≅ ΔPQB (by AAS congruence criterion)
⇒ A(ΔRSC) = A(ΔPQB)

