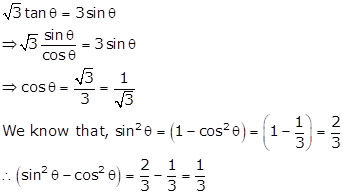Class 10 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 10 - Trigonometric Ratios
Trigonometric Ratios Exercise Ex. 10
Solution 1
Given: 
Let us draw a 
ABC in which 
B = 90o and BAC =
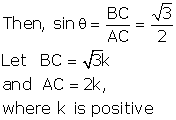
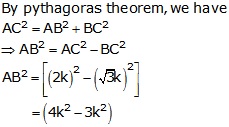
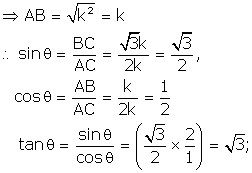
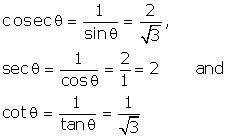
Solution 2
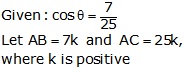
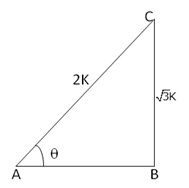
Let us draw a 
ABC in which 
B = 90o and BAC = 
By Pythagoras theorem, we have
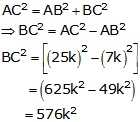
Solution 3
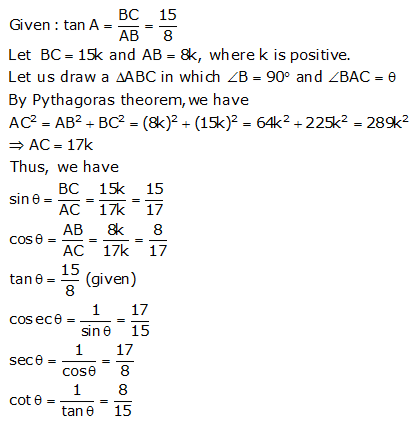
Solution 4
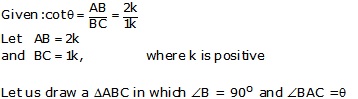
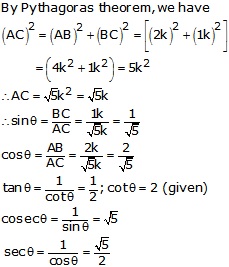
Solution 5
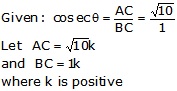
Let us draw a 
ABC in which 
B = 90o and BAC = 
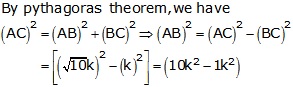
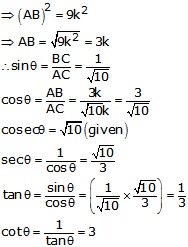
Solution 6
Solution 7
……
given
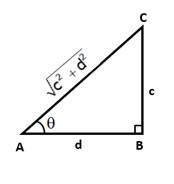
In right ∆ABC, ∠B = 90° and ∠A = θ
Let BC = c and AC =
Then, AB2 = AC2 - BC2 = c2 + d2 - c2 = d2
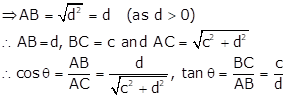
Solution 8
In right ∆ABC, ∠B = 90° and ∠A = θ
√3 tan θ = 1 ⇒ tan
θ = 
Let BC = k and AB = √3k
Then, AC2 = AB2 + BC2 = 3k2 + k2 = 4k2
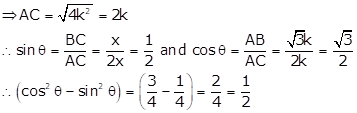
Solution 9
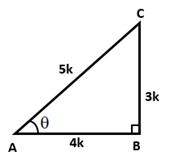
In right ∆ABC, ∠B = 90° and ∠A = θ
4 tan θ = 3 ⇒ tan θ
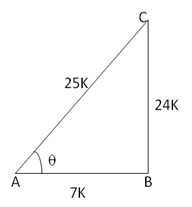
Let BC = 3k and AB = 4k
Then, AC2 = AB2 + BC2 = 16k2 + 9k2 = 25k2
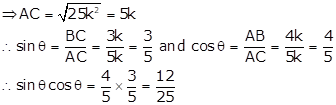
Solution 10
Solution 11
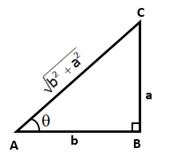
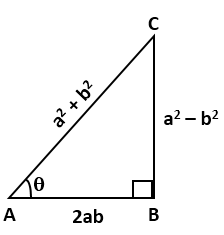
In right ∆ABC, ∠B = 90° and ∠A = θ
AC2 = AB2 + BC2 = b2 + a2
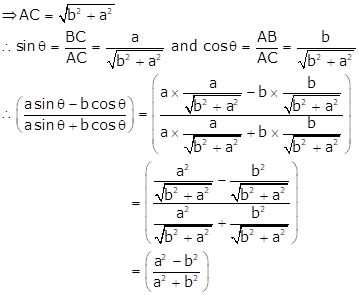
Solution 12
Now,
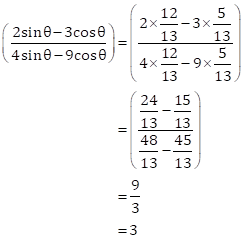
Solution 13
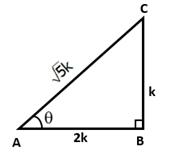
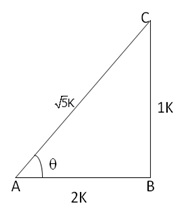
In right ∆ABC, ∠B = 90° and ∠A = θ
Let BC = k and AB = 2k
Then, AC2 = AB2 + BC2 = (4k2 + k2)= 5k2
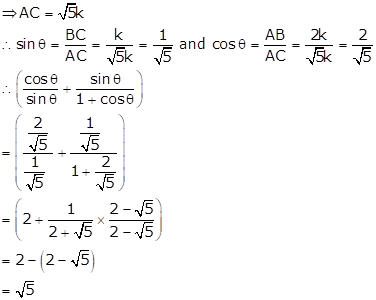
Solution 14
Solution 15
Given: 
Let us draw a triangle ABC in which 
B = 90o and A = 
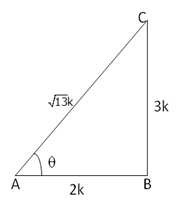
By Pythagoras theorem, we have
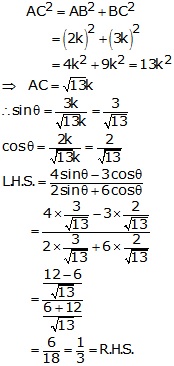
Solution 16
Given: 
Let us draw a triangle ABC in which 
B = 90o and A = 
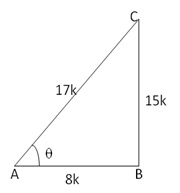
By Pythagoras theorem, we have
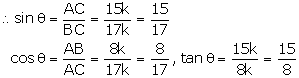
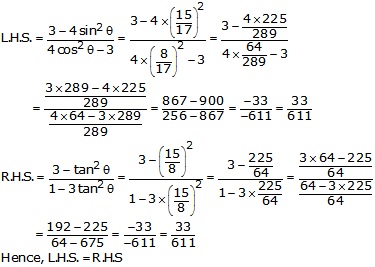
Solution 17
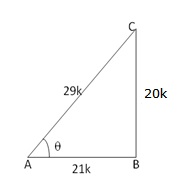
Given: 
Let us draw a triangle ABC in which 
B = 90o and A = 
By Pythagoras theorem, we have
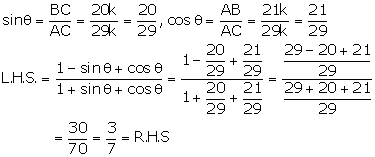
Solution 18
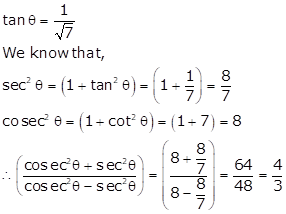
Solution 19
Let BC = 3k and AC = 4k
Then, AB2 = AC2 - BC2 = (16k2 - 9k2)= 7k2
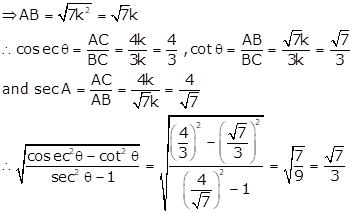
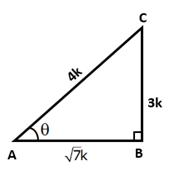
Solution 20(i)
In right ∆ABC, ∠B = 90° and ∠A = θ
Let BC = 4k and AB = 3k
Then, AC2 = AB2 + BC2 = (9k2 + 16k2)= 25k2
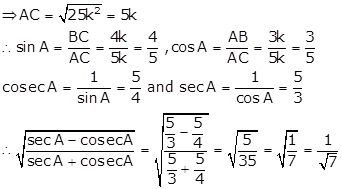
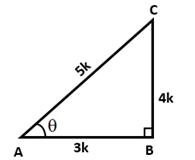
Solution 20(ii)
In right ∆ABC, ∠B = 90° and ∠A = θ
Let BC = 4k and AB = 3k
Then, AC2 = AB2 + BC2 = (9k2 + 16k2)= 25k2
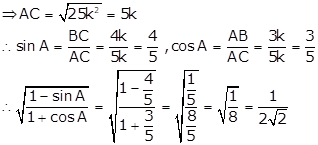
Solution 21
Solution 22
In right ∆ABC, ∠B = 90° and tan A = 1
Let BC = k and AB = k
Then, AC2 = AB2 + BC2 = (k2 + k2)= 2k2
Solution 23
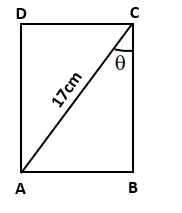
In right ∆ABC, ∠B = 90°
Then, BC2 = AC2 - AB2 = (17)2 - (8)2= 289 - 64 = 225
⇒ BC = √225 = 15 cm
Therefore Length = 15 cm and Breadth = 8 cm
(i) The area of rect. ABCD = Length × Breadth = 15 × 8 = 120 cm2
(ii) The perimeter of rect. ABCD =2(l + b) = 2(15 + 8) = 46 cm
Solution 24
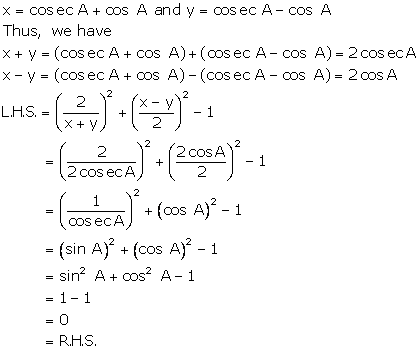
Solution 25
Solution 26
In right-angled ΔABC,
AB2 + BC2 = AC2
⇒ AB2 + x2 = (x + 2)2
⇒ AB2 + x2 = x2 + 4 + 4x
⇒ AB2 = 4(x + 1)
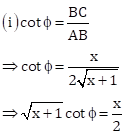
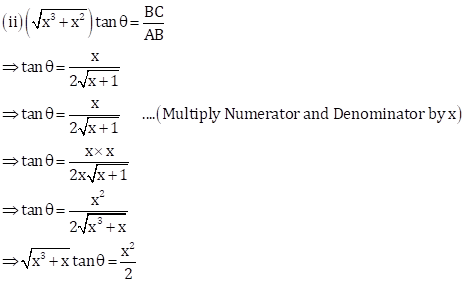
Solution 27
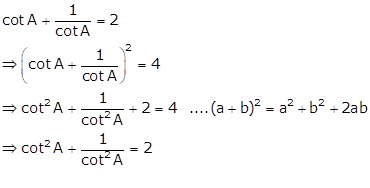
Solution 28
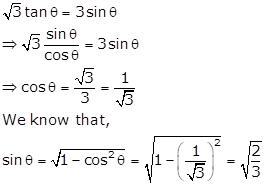
Solution 29
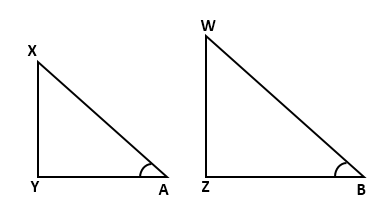
Consider two right triangles XAY and WBZ such that sin A = sin B
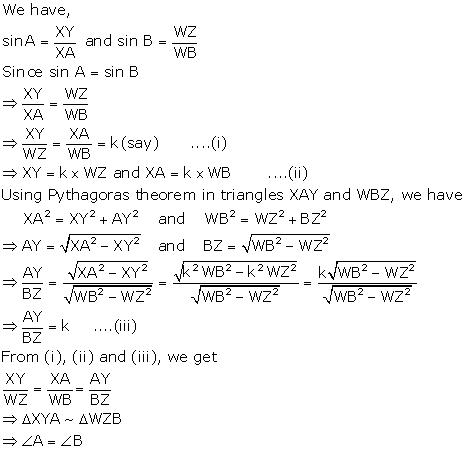
Solution 30
Consider two right triangles XAY and WBZ such that tan A = tan B
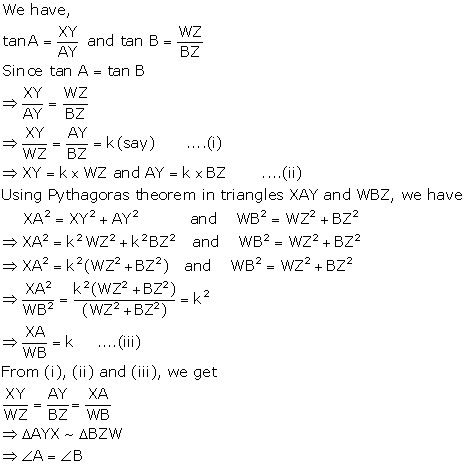
Solution 31
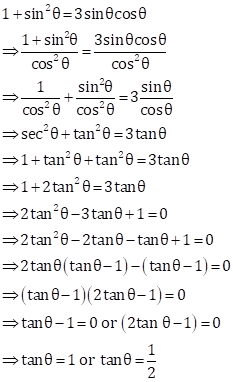
Trigonometric Ratios Exercise MCQ
Solution 1
Correct Option: (c)
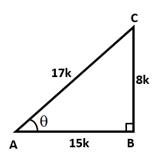
Let BC = 8k and AB = 15k
Then, AC2 = AB2 + BC2 = (225k2 + 64k2) = 289k2
⇒ AC2 =289k2
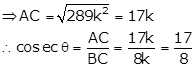
Solution 2
Correct Option: (a)
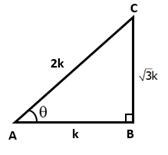
tan θ 
Let BC = √3k and AB = k
Then, AC2 = AB2 + BC2 = (k2 + 3k2) = 4k2
⇒ AC2 =4k2
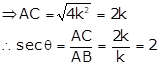
Solution 3
Correct Option: (d)
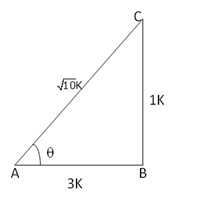
cosec θ = √10
Let BC = k and AC = √10k
Then, AB2 = AC2 - BC2 = (10k2 - k2) = 9k2
⇒ AB2 =9k2
⇒ AB = √9k2 = 3k
Solution 4
Correct Option: (b)
Solution 5
Correct option: (c)
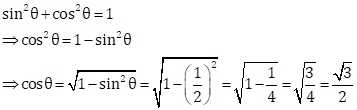
Now,
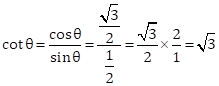
Solution 6
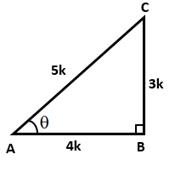
Correct Option: (a)
Let AB = 4k and AC = 5k
Then, BC2 = AC2 - AB2 = (25k2 - 16k2) = 9k2
⇒ BC = √9k2 = 3k
Solution 7
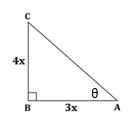
Correct option: (c)
∴ length of BC = 4x, length of AB = 3x
Now,
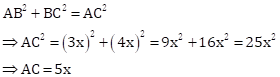
So,
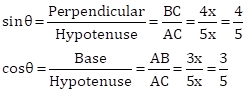
Solution 8
Correct Option: (d)
(tan θ + cot θ) = 5
⇒ (tan θ + cot θ)2 = 52
⇒ tan2 θ + cot2 θ + 2 tan θ cot θ = 25
⇒ tan2 θ + cot2 θ + 2 tan θ ×
⇒ tan2 θ + cot2 θ + 2 = 25
⇒ tan2 θ + cot2 θ = 23
Solution 9
Correct Option: (a)
(cosθ + sec θ) = 
⇒ (cosθ + sec θ)2 = 
⇒ cos2 θ + sec2 θ + 2 cos θ sec θ = 
⇒ tan2 θ + cot2 θ + 2 cos θ × 
⇒ tan2 θ + cot2 θ + 2 =
⇒ tan2 θ + cot2 θ = 
Solution 10
Correct Option: (b)
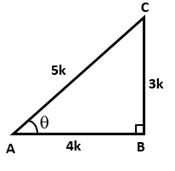
Let BC = 3k and AB = 4k
Then, AC2 = AB2 + BC2 = (4k2 + 3k2) = 25k2
Solution 11
Correct Option: (c)
Solution 12
Correct Option: (a)
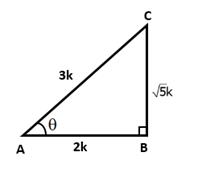
Let AB = 2k and AC = 3k
Then, BC2 = AC2 - AB2 = (9k2 - 4k2) = 5k2
Solution 13
Correct Option: (b)
We have, sec θ + tan θ + 1 = 0 ⇒ sec θ + tan θ = -1
We know that,
(sec2 θ - tan2 θ) = 1
⇒ (sec θ - tan θ)(sec θ + tan θ) = 1
⇒ (sec θ - tan θ) × -1 = 1
⇒ (sec θ - tan θ) = -1
Solution 14
Correct Option: (c)
cos A + cos2 A = 1 …. given
⇒ cos A = (1 - cos2 A) = sin2 A
∴ (sin2 A + sin4 A) = (cos A + cos2 A) = 1
Solution 15
Correct Option: (d)
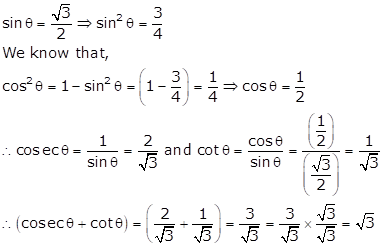
Solution 16
Correct Option: (a)
