Class 10 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 7 - Triangles
Triangles Exercise Ex. 7A
Solution 1
(i)In ![]() ABC, DE || BC, AD = 3.6 cm, AB = 10 cm, AE = 4.5 cm
ABC, DE || BC, AD = 3.6 cm, AB = 10 cm, AE = 4.5 cm

Hence, AC = 12.5 cm and EC = 8cm
(ii)In ![]() ABC, DE || BC, AB = 13.3 cm, AC = 11.9 cm and EC = 5.1 cm
ABC, DE || BC, AB = 13.3 cm, AC = 11.9 cm and EC = 5.1 cm

Hence, AD = 7.7 cm
(iii)In ![]() ABC, DE || BC, AC = 6.6 cm,
ABC, DE || BC, AC = 6.6 cm, ![]()
?
Hence, AE = 2.4 cm
(iv)In ![]() ABC, DE || BC, Given
ABC, DE || BC, Given ![]()

Hence AE = 4 cm
Solution 2
(i)D and E are points on the sides AB and AC respectively of a ![]() ABC such that DE || BC, AD = x cm, DB = (x - 2) cm,
ABC such that DE || BC, AD = x cm, DB = (x - 2) cm,
AE = (x + 2) cm, EC = (x - 1) cm

Hence, x = 4
(ii)In ![]() ABC, DE || BC, AD = 4 cm, DB = (x - 4) cm, AE = 8 cm, EC = (3x - 19) cm
ABC, DE || BC, AD = 4 cm, DB = (x - 4) cm, AE = 8 cm, EC = (3x - 19) cm

Hence, x = 11
(iii)In ![]() ABC, DE || BC, AD = (7x - 4) cm, AE = (5x - 2) cm, DB = (3x + 4)cm, EC = 3x cm
ABC, DE || BC, AD = (7x - 4) cm, AE = (5x - 2) cm, DB = (3x + 4)cm, EC = 3x cm
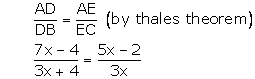

Solution 3
Given: A ![]() ABC in which D and E are points on the sides AB and AC respectively.
ABC in which D and E are points on the sides AB and AC respectively.
To prove: DE ||BC
Proof:
(i)AD = 5.7 cm, DB = 9.5 cm, AE = 4.8 cm and EC = 8 cm
Since D and E are the points on AB and AC respectively.

Hence, by the converse of Thales theorem DE || BC
(ii)AB = 11.7 cm, AC = 11.2 cm, BD = 6.5 cm, AE = 4.2 cm
Since D and E are points on AB and AC respectively.

Hence, by the converse of Thales theorem DE is not parallel to BC.
(iii) AB = 10.8 cm, AD = 6.3 cm, AC = 9.6 cm, EC = 4 cm
Since D and E are the points on AB and AC respectively.

Hence by the converse of Thales theorem DE || BC
(iv)AD = 7.2 cm, AE = 6.4 cm, AB = 12 cm, AC = 10 cm
Since D and E are points on the side AB and AC respectively.
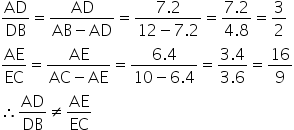
Hence, by the converse of Thales theorem DB is not parallel to BC
Solution 4
(i) AB = 6.4 cm, AC = 8 cm, BD = 5.6 cm
Let BC = x
Now, DC = (BC - BD)
= (x - 5.6) cm
In ![]() ABC, AD is the base for of
ABC, AD is the base for of ![]() A
A
So, by the angle bisector theorem, We have
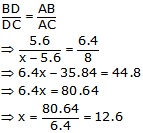
Hence, BC = 12.6 cm and DC = (12.6 - 5.6) cm = 7 cm
(ii) AB = 10 cm, AC = 14 cm, BC = 6cm
Let BD = x,
DC = (BC - BD) = (6 - x) cm
In ![]() ABC, AD is the bisector of ?
ABC, AD is the bisector of ?![]() ?A
?A
So, By angle bisector theorem,
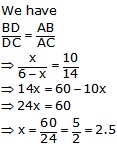
Hence, BD = 2.5 cm and DC = (6 - 2.5) cm = 3.5 cm
(iii)AB = 5.6 cm, BD = 3.2 cm and BC = 6 cm
DC = BC - BD = (6 - 3.2) cm = 2.8 cm
Let AC = x,
In ![]() ABC, AD is the bisector of
ABC, AD is the bisector of ![]() A
A
So, by the angle bisector theorem we have

Hence, AC = 4.9 cm
(iv)AB = 5.6 cm, AC = 4 cm, DC = 3 cm
Let BD = x,
In ![]() ABC, AD is the bisector of
ABC, AD is the bisector of ![]() A
A
So, by the angle bisector theorem, we have
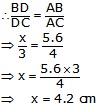
Hence, BD = 4.2 cm
So BC = BD + AC = (4.2 + 3) cm
![]() BC = 7.2 cm
BC = 7.2 cm
Solution 5

Solution 6
Let ABCD be the trapezium and let E and F be the midpoints of AD and BC respectively.
Const: Produce AD and BC to meet at P
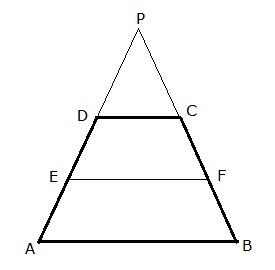
In ![]() PAB, DC || AB
PAB, DC || AB

Solution 7
CD || AB in trapezium ABCD and its diagonals intersect at O.
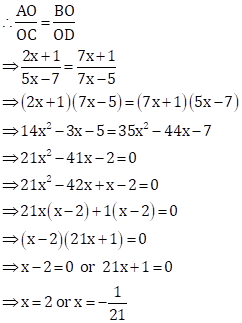
But, ![]() will make DO =
will make DO = ![]()
And, length cannot be negative.
![]()
Solution 8
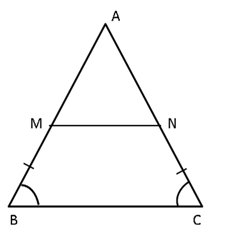

Solution 9
?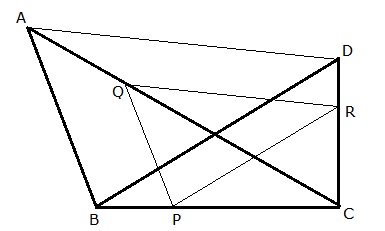
Given: ![]() ABC and
ABC and ![]() DBC lie on the same side of BC. P is a point on BC, PQ || AB and PR || BD are drawn meeting AC at Q and CD at R respectively.
DBC lie on the same side of BC. P is a point on BC, PQ || AB and PR || BD are drawn meeting AC at Q and CD at R respectively.
To Prove: QR || AD
Proof: In ![]() ABC
ABC

Hence, in ![]() ACD, Q and R the points in AC and CD such that
ACD, Q and R the points in AC and CD such that
![]()
![]() QR || AD(by the converse of Thales theorem)
QR || AD(by the converse of Thales theorem)
Hence proved.
Solution 10
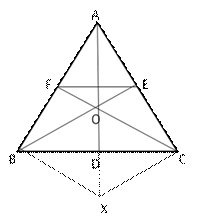
Given BD = CD and OD = DX
Join BX and CX
Thus, the diagonals of quad OBXC bisect each other
![]() OBXC is a parallelogram
OBXC is a parallelogram
![]() BX || CF and so, OF || BX
BX || CF and so, OF || BX
Similarly, CX || OE
In ![]() ABX, OF || BX
ABX, OF || BX
Solution 11
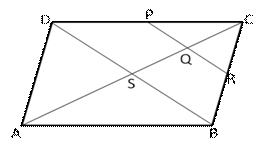
Given: ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that![]() . PQ produced meets BC at R.
. PQ produced meets BC at R.
To prove: R is the midpoint of BC
Construction: Join BD
Proof: Since the diagonals of a || gm bisect each other at S such that
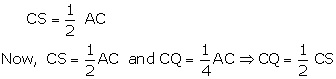
![]() Q is the midpoint of CS
Q is the midpoint of CS
So, PQ || DS.
Therefore, QR || SB.
In ![]() CSB, Q is the midpoint of CS and QR || SB.
CSB, Q is the midpoint of CS and QR || SB.
So R is the midpoint of BC.
Solution 12
Given: ABC is a triangle in which AB = AC. D and E are points on AB and AC respectively such that AD = AE
To prove: The points B, C, E and D are concyclic.
Proof: AB = AC (given)
AD = AE (given)

![]() Quad BCEA is cyclic
Quad BCEA is cyclic
Hence, the point B, C, E, D are concyclic
Solution 13

Triangles Exercise Ex. 7B
Solution 1
(i)In ![]() ABC and
ABC and ![]() PQR
PQR
![]() A =
A = ![]() Q = 50°
Q = 50°
![]() B =
B = ![]() P = 60°
P = 60°
![]() C =
C = ![]() R = 70°
R = 70°
![]()
![]() ABC ~
ABC ~![]() QPR(by AAA similarity)
QPR(by AAA similarity)
(ii)In ![]() ABC and
ABC and ![]() EFD
EFD
![]() A =
A = ![]() D = 70°
D = 70°
SAS: Similarity condition is not satisfied as ![]() A and
A and ![]() D are not included angles.
D are not included angles.
(iii)![]() CAB
CAB ![]()
![]() QRP (SAS Similarity)
QRP (SAS Similarity)
![]()
(iv) In ![]() EFD and
EFD and ![]() PQR
PQR
FE = 2cm, FD = 3 cm, ED = 2.5 cm
PQ = 4 cm, PR = 6 cm, QR = 5 cm
![]()
![]()
![]() FED ~
FED ~![]() PQR (SSS similarity)
PQR (SSS similarity)
(v)
In ![]() CAB and
CAB and ![]() RMN
RMN

Solution 2
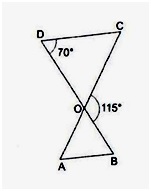
![]() ODC ~
ODC ~ ![]() OBC
OBC
![]() BOC = 115o
BOC = 115o
![]() CDO = 70o
CDO = 70o
(i) ![]() DOC = (180o -
DOC = (180o - ![]() BOC)
BOC)
= (180o - 115o)
= 65o
(ii) ![]() OCD = 180o -
OCD = 180o - ![]() CDO -
CDO - ![]() DOC
DOC
![]() OCD = 180o - (70o + 65o)
OCD = 180o - (70o + 65o)
= 45o
(iii) Now, ![]() ABO ~
ABO ~ ![]() ODC
ODC
![]() AOB =
AOB = ![]() COD (vert. Opp
COD (vert. Opp ![]() s) = 65o
s) = 65o
![]() OAB =
OAB = ![]() OCD = 45o
OCD = 45o
(iv) ![]() OBA =
OBA = ![]() ODC(alternate angles) = 70o
ODC(alternate angles) = 70o
So, ![]() OAB = 45o and
OAB = 45o and ![]() OBA = 70o
OBA = 70o
Solution 3
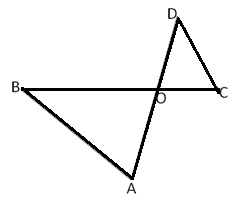
Given: ![]() OAB
OAB ![]()
![]() OCD
OCD
AB = 8 cm, BO = 6.4 cm, CD = 5 cm, OC = 3.5 cm

Solution 4
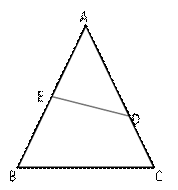
Given: ![]() ADE =
ADE = ![]() B, AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm, BC = 4.2 cm
B, AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm, BC = 4.2 cm
Proof:
In ![]() ADE and
ADE and ![]() ABC,
ABC,
![]() A =
A = ![]() A (common)
A (common)
![]() ADE =
ADE = ![]() B (given)
B (given)
Therefore, ![]() ADE
ADE ![]()
![]() ABC (AA Criterion)
ABC (AA Criterion)

Hence, DE = 2.8 cm
Solution 5
![]() ABC and
ABC and ![]() PQR are similar triangles, therefore corresponding sides of both the triangles are proportional.
PQR are similar triangles, therefore corresponding sides of both the triangles are proportional.

Hence, AB = 16 cm
Solution 6
![]() ABC and
ABC and ![]() DEF are two similar triangles, therefore corresponding sides of both the triangles are proportional.
DEF are two similar triangles, therefore corresponding sides of both the triangles are proportional.
Hence, ![]()
Let perimeter of ![]() ABC = x cm
ABC = x cm
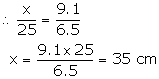
Hence, perimeter of ![]() ABC = 35 cm
ABC = 35 cm
Solution 7

Given: AB = 100 cm, BC = 125 cm, AC = 75 cm
Proof:
In ![]() BAC and
BAC and ![]() BDA
BDA
![]() BAC =
BAC = ![]() BDA = 90o
BDA = 90o
![]() B =
B = ![]() B (common)
B (common)
![]() BAC
BAC ![]()
![]() BDA(by AA similarities)
BDA(by AA similarities)

Therefore, AD = 60 cm
Solution 8
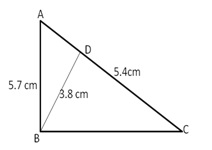
Given that AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm
In ![]() CBA and
CBA and ![]() CDB
CDB
![]() CBA =
CBA = ![]() CDB = 90o
CDB = 90o
![]() C =
C = ![]() C (Common)
C (Common)
Therefore, ![]() CBA
CBA ![]()
![]() CDB (by AA similarities)
CDB (by AA similarities)

Hence, BC = 8.1 cm
Solution 9
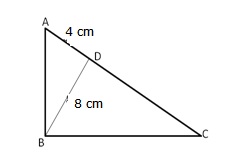
Given that BD = 8 cm, AD = 4 cm
In ![]() DBA and
DBA and ![]() DCB, we have
DCB, we have
![]() BDA =
BDA = ![]() CDB = 90o
CDB = 90o
![]() DBA =
DBA = ![]() DCB [each = 90o -
DCB [each = 90o - ![]() A]
A]
![]()
![]() DBA
DBA ![]()
![]() DCB (by AAA similarity)
DCB (by AAA similarity)

Hence, CD = 16 cm
Solution 10

Given: P is a point on AB.
Then, AB = AP + PB = (2 + 4) cm = 6 cm
Also Q is a point on AC.
Then, AC = AQ + QC = (3 + 6) cm = 9 cm

Thus, in ![]() APQ and
APQ and ![]() ABC
ABC
![]() A =
A = ![]() A (common)
A (common)
And![]()
![]()
![]() APQ ~
APQ ~ ![]() ABC(by SAS similarity)
ABC(by SAS similarity)
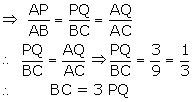
Hence proved.
Solution 11
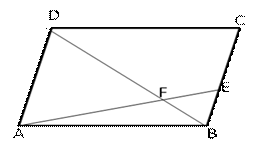
Given: ABCD is a parallelogram and E is point on BC. Diagonal DB intersects AE at F.
To Prove: AF × FB = EF × FD
Proof: In ![]() AFD and
AFD and ![]() EFB
EFB
![]() AFD =
AFD = ![]() EFB (vertically opposite
EFB (vertically opposite ![]() s)
s)
![]() DAF =
DAF = ![]() BEF (Alternate
BEF (Alternate ![]() s)
s)

Hence proved.
Solution 12
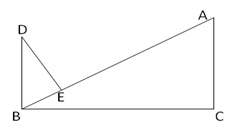
In the given figure: DB ![]() BC, AC
BC, AC ![]() BC and DB || AC
BC and DB || AC
![]()
AB is the transversal
![]()
![]() DBE =
DBE = ![]() BAC [Alternate
BAC [Alternate ![]() s]
s]
In ![]() BDE and
BDE and ![]() ABC
ABC
![]() DEB =
DEB = ![]() ACB = 90o
ACB = 90o
![]() DBE =
DBE = ![]() BAC
BAC
![]() BDE ~
BDE ~ ![]() ABC
ABC
![]() ~
~ ![]() [By AA similarity]
[By AA similarity]
![]()
Hence proved.
Solution 13
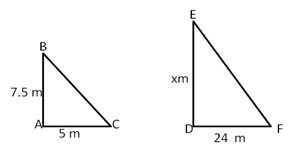
Let AB be the vertical stick and let AC be its shadow.
Then, AB = 7.5 m and AC = 5 m
Let DE be the vertical tower and let DF be its shadow
Then,DF = 24 m, Let DE = x meters
Now, in ![]() BAC and
BAC and ![]() EDF,
EDF,
![]() BAC ~
BAC ~ ![]() EDF by SAS criterion
EDF by SAS criterion
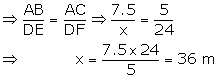
Therefore, height of the vertical tower is 36 m.
Solution 14
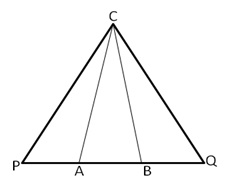
In ![]() ACP and
ACP and ![]() BCQ
BCQ
CA = CB
![]()
![]() CAB =
CAB = ![]() CBA
CBA

![]()
![]() ACP
ACP ![]()
![]() BCQ
BCQ
Solution 15
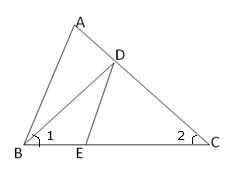
![]() 1 =
1 = ![]() 2 (given)
2 (given)
![]() (given)
(given)
Also, ![]() 2 =
2 = ![]() 1
1 ![]()
![]()
Therefore, by SAS similarity criterion ![]() ACB ~
ACB ~ ![]() DCE
DCE
Solution 16
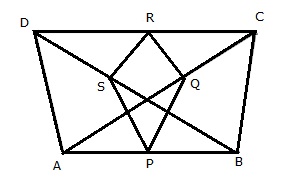
Given: ABCD is a quadrilateral in which AD = BC. P, Q , R, S are the midpoints of AB, AC, CD and BD.
To prove: PQRS is a rhombus
Proof: In ![]() ABC,
ABC,
Since P and Q are mid points of AB and AC
Therefore, PQ || BC and ![]() (Mid-point theorem)
(Mid-point theorem)
Similarly,

![]() SP || RQ and PQ || SR and PQ = RQ = SP = SR
SP || RQ and PQ || SR and PQ = RQ = SP = SR
Hence,PQRS is a rhombus.
Solution 17

Solution 18

Solution 19
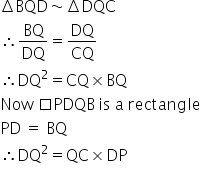
Solution 20
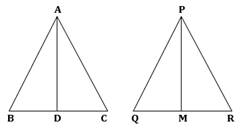
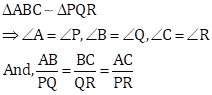
Consider
![]()

Therefore, by SAS criterion of similarity,
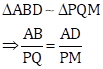
Solution 21
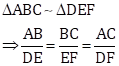
Consider
![]()
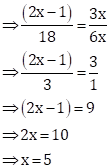
Then, we have
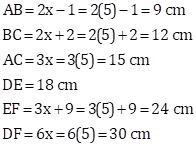
Triangles Exercise Ex. 7C
Solution 1
Given: ![]() ABC
ABC ![]()
![]() DEF,
DEF,
area of ![]() ABC=
ABC= ![]() and area of
and area of ![]() DEF = 121
DEF = 121![]()
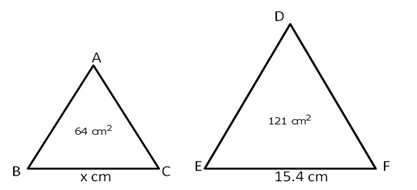
We know that the ratio of the area of two similar triangles is equal to the ratio of the squares of their corresponding sides.

Hence, BC = 11.2 cm
Solution 2
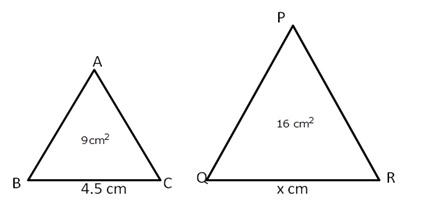
Given: ![]() ABC
ABC ![]()
![]() PQR,
PQR,
area of ![]() ABC = 9 cm2 and area of
ABC = 9 cm2 and area of ![]() PQR = 16 cm2.
PQR = 16 cm2.
We know that the ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

Hence, QR = 6 cm
Solution 3
Given: ![]() ABC ~
ABC ~![]() PQR,
PQR,
area of ![]() ABC = 4 area of
ABC = 4 area of ![]() PQR.
PQR.
Let area of ![]() PQR = x. Then area of
PQR = x. Then area of ![]() ABC = 4x.
ABC = 4x.
We know that the ratio of the areas of two similar triangle is equal to the ratio of the square of their corresponding sides.
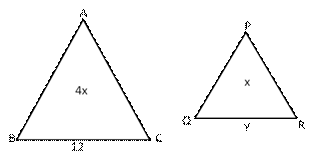

![]()
Hence. QR = 6 cm
Solution 4
Given: ![]() ABC
ABC ![]()
![]() DEF such that ar(
DEF such that ar(![]() ABC) = 169
ABC) = 169![]() and ar(
and ar(![]() DEF) = 121
DEF) = 121 ![]()
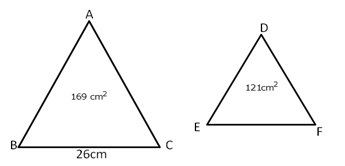
We know that the ratio of the area of similar triangles is equal to the ratio of the square of their corresponding sides.
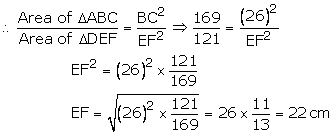
Hence, the longest side of smallest triangle side is 22 cm.
Solution 5
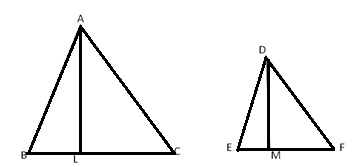
Given: ![]() ABC
ABC ![]()
![]() DEF
DEF
ar(![]() ABC) = 100 and ar(
ABC) = 100 and ar(![]() DEF) = 49
DEF) = 49
Let AL and DM be the corresponding altitude of ![]() ABC and
ABC and ![]() DEF respectively such that AL = 5 cm and let DM = x cm
DEF respectively such that AL = 5 cm and let DM = x cm
We know that the ratio of the area of two similar triangles is equal to the ratio of the square of corresponding altitudes.
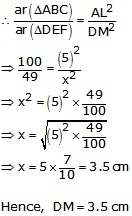
Therefore, the required altitude is 3.5 cm
Solution 6
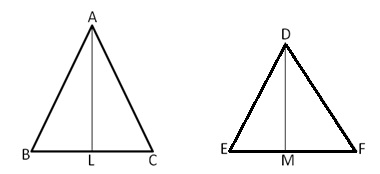
Given: ![]() ABC
ABC ![]()
![]() DEF
DEF
Let AL and DM be the corresponding altitudes of ![]() ABC and
ABC and ![]() DEF respectively such that AL = 6 cm and DM = 9 cm.
DEF respectively such that AL = 6 cm and DM = 9 cm.
We know that the ratio of squares of altitudes of two similar triangles is equal to the ratio of the corresponding areas.

Hence, ratio of their areas = 4 : 9
Solution 7
Given: ![]() ABC
ABC ![]()
![]() DEF such that
DEF such that
ar(![]() ABC) = 81
ABC) = 81![]() and ar(
and ar(![]() DEF) = 49
DEF) = 49![]()
Let AL and DM be the corresponding altitudes of ![]() ABC and
ABC and ![]() DEF respectively, such that AL = 6.3 cm and Let DM= x cm
DEF respectively, such that AL = 6.3 cm and Let DM= x cm
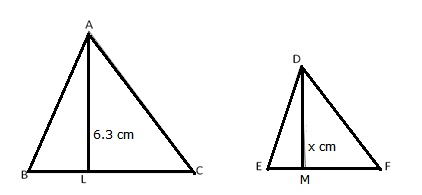
We know that the ratio of the area of two similar triangles is equal to the ratio of the square of corresponding altitudes:

Hence, the required altitude 4.9 cm
Solution 8
Given: ![]() ABC
ABC ![]()
![]() DEF such that ar(
DEF such that ar(![]() ABC) = 100 cm and ar(
ABC) = 100 cm and ar(![]() DEF) = 64
DEF) = 64![]()
Let AP and DQ be the corresponding medians of ![]() ABC and
ABC and ![]() DEF respectively such that DQ = 5.6cm.
DEF respectively such that DQ = 5.6cm.
Let AP = x cm.
We know that the ratio of the areas of two similar triangle is equal be the ratio of the squares of their corresponding medians.
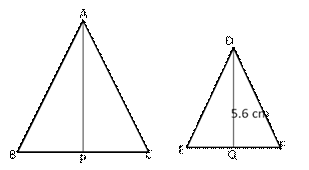

Hence, AP = 7 cm
Solution 9
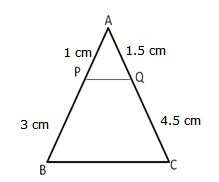
Given: AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 cm
AB = AP + PB = (1 + 3) cm = 4 cm
AC = AQ + QC = (1.5 + 4.5) cm = 6 cm

In ![]() APQ and
APQ and ![]() ABC, we have
ABC, we have
![]() APQ =
APQ = ![]() ABC (corresponding
ABC (corresponding ![]() s)
s)
![]() AQP =
AQP = ![]() ACB (corresponding
ACB (corresponding ![]() s)
s)
![]()
![]() APQ
APQ ![]()
![]() ABC [by AA similarity]
ABC [by AA similarity]
Hence proved.
Solution 10

Given DE || BC
DE = 3 cm and BC = 6 cm
ar(![]() ADE) = 15
ADE) = 15![]()
In ![]() ADE and
ADE and ![]() ABC, we have
ABC, we have

Solution 11
In ![]() BAC and
BAC and ![]() ADC, we have
ADC, we have
![]() BAC =
BAC = ![]() ADC = 90o (AD
ADC = 90o (AD ![]() BC)
BC)
![]() ACB =
ACB = ![]() DCA (common)
DCA (common)
![]() BAC
BAC ![]()
![]() ADC
ADC
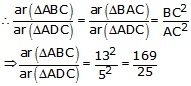
Therefore, the ratio of the areas of ![]() ABC and
ABC and ![]() ADC = 169:25
ADC = 169:25
Solution 12
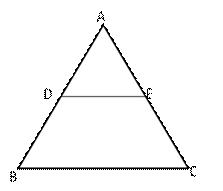
Let DE = 3x and BC = 5x
In ![]() ADE and
ADE and ![]() ABC, we have
ABC, we have
![]() ADE =
ADE = ![]() ABC (corres.
ABC (corres. ![]() s)
s)
![]() AED =
AED = ![]() ACB (corres.
ACB (corres. ![]() s)
s)
![]()
![]() ADE
ADE ![]()
![]() ABC (by AA similarity)
ABC (by AA similarity)
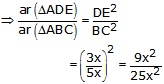
Let, ar(![]() ADE) = 9x2 units
ADE) = 9x2 units
Then, ar(![]() ABC) = 25x2 units
ABC) = 25x2 units
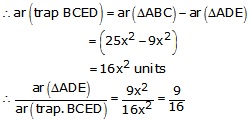
Therefore, ratio of ar(![]() ADE) to the ar(trap BCED) = 9:16
ADE) to the ar(trap BCED) = 9:16
Solution 13
In ![]() ABC, D and E are midpoint of AB and AC respectively.
ABC, D and E are midpoint of AB and AC respectively.
So, DE|| BC and ![]()
Now, in ![]() ADE and
ADE and ![]() ABC, we have
ABC, we have
![]() ADE =
ADE = ![]() ABC (corres.
ABC (corres. ![]() s)
s)
![]() AED =
AED = ![]() ACB (corres.
ACB (corres. ![]() s)
s)
![]()
![]() ADE
ADE ![]()
![]() ABC (by AA similarity)
ABC (by AA similarity)
Let AD = x and AB = 2x

Therefore, the ratio of the areas of ![]() ADE and
ADE and ![]() ABC = 1:4
ABC = 1:4
Triangles Exercise Ex. 7D
Solution 1
For a given triangle to be a right angled, the sum of the squares of the two sides must be equal to the square of the largest side.
(i)Let a = 9cm, b = 16 cm and c = 18 cm. Then

Hence the given triangle is not right angled.
(ii)Let a = 7cm, b = 24 cm and c = 25 cm, Then

Hence, the given triangle is a right triangle.
(iii)Let a = 1.4 cm, b = 4.8 cm, and c = 5 cm
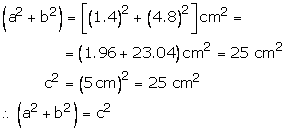
Hence, the given triangle is a right triangle
(iv)Let a = 1.6 cm, b = 3.8 cm and c = 4 cm
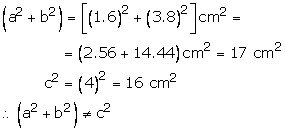
Hence, the given triangle is not a right triangle
(v)Let p = (a - 1) cm, q = ![]() cm and r = (a + 1)
cm and r = (a + 1) ![]()
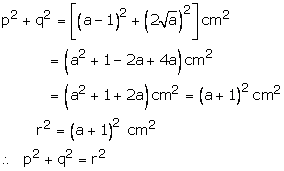
Hence, the given triangle is a right triangle
Solution 2
Starting from A, let the man goes from A to B and from B to C, as shown in the figure.
Then,
AB = 80 m, BC = 150 m and![]() ABC = 90o
ABC = 90o
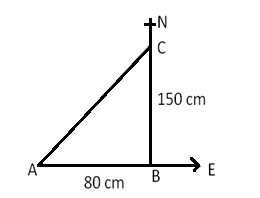
From right ![]() ABC, we have
ABC, we have

![]()
Hence, the man is 170m north-east from the starting point.
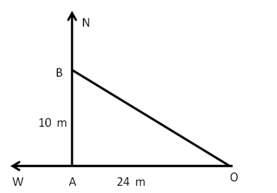
Solution 3
Starting from O, let the man goes from O to A and then A to B as shown in the figure.
Then,
OA = 10 m, AB = 24 m and ![]() OAB = 90o
OAB = 90o
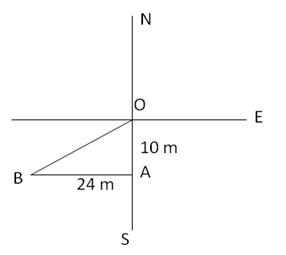
Using Pythagoras theorem:
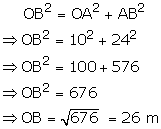
Hence, the man is 26 m south-west from the starting position.
Solution 4
Let AB be the building and CB be the ladder.
Then,
AB = 12 m, CB = 13 m and ![]() CAB = 90o
CAB = 90o
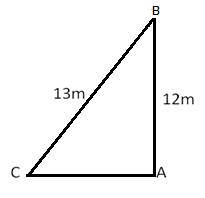
By Pythagoras theorem, we have
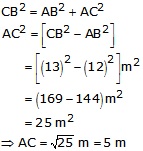
Hence, the distance of the foot of the ladder from the building is 5 m.
Solution 5
Let AB be the wall where window is at B, CB be the ladder and AC be the distance between the foot of the ladder and wall.
Then,
AB = 20 m, AC = 15 m, and ![]() CAB = 90o
CAB = 90o
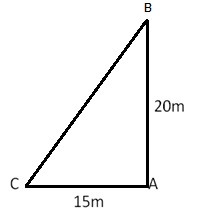
By Pythagoras theorem, we have
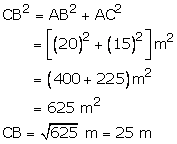
Hence, the length of ladder is 25 m.
Solution 6
Let AB and CD be the given vertical poles.
Then,
AB = 9 m, CD = 14 m and AC = 12 m
Const: Draw, BE || AC.
Then,
CE = AB = 9m and BE = AC = 12 m
![]() DE = (CD - CE)
DE = (CD - CE)
= (14 - 9)
= 5 m
In right ![]() BED, we have
BED, we have

Hence, the distance between their tops is 13 m.
Solution 7

Solution 8
In ![]() PQR,
PQR, ![]() QPR = 90o, PQ = 24 cm, and QR =
QPR = 90o, PQ = 24 cm, and QR = ![]()
In ![]() POR, PO = 6 cm, QR = 8cm and
POR, PO = 6 cm, QR = 8cm and ![]() POR = 90o
POR = 90o
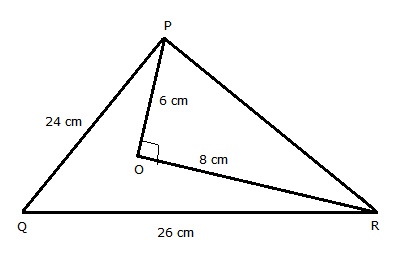
In ![]() POR,
POR,

In ![]() PQR,
PQR,
By Pythagoras theorem, we have

Hence, ![]()
(sum of square of two sides equal to square of greatest side)
Hence, ![]() PQR is a right triangle which is right angled at P.
PQR is a right triangle which is right angled at P.
Solution 9
Given: ![]() ABC is an isosceles triangle with AB = AC = 13
ABC is an isosceles triangle with AB = AC = 13 ![]()
Const: Draw altitude from A to BC (AL ![]() BC).
BC).
Now, AL = 5 cm
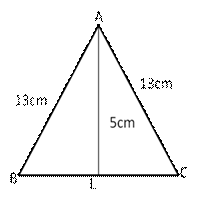
In ![]() ALB,
ALB,
![]() ALB = 90o
ALB = 90o

In ![]() ALC,
ALC,
![]() ALC = 90o
ALC = 90o

Solution 10
Given: ![]() ABC in which AB = AC = 2a units and BC = a units
ABC in which AB = AC = 2a units and BC = a units
Const: Draw AD ![]() BC then D is the midpoint of BC.
BC then D is the midpoint of BC.
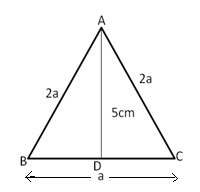
In ![]() ABC
ABC

Solution 11
In an equilateral triangle all sides are equal.
Then, AB = BC = AC = 2a units
Const: Draw an altitude AD ![]() BC
BC
Given BC = 2a. Then, BD = a
In ![]() ABD,
ABD,
![]() ADB = 90o
ADB = 90o

Hence, the length of each altitude is ![]()
Solution 12
![]() ABC is an equilateral triangle in which all side are equa.
ABC is an equilateral triangle in which all side are equa.
Therefore, AB = BC = AC = 12 cm
If BC = 12 cm
Then, BD = DC = 6 cm
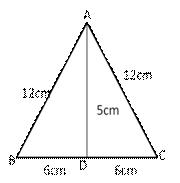
In ![]() ADB,
ADB,
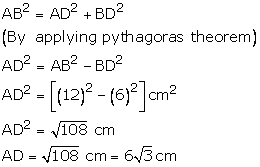
Hence the height of the triangle is ![]()
Solution 13
Let ABCD is the given rectangle, let BD is a diagonal making a ![]() ADB.
ADB.
![]()
![]() BAD = 90o
BAD = 90o
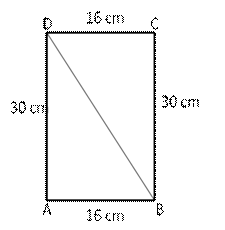
Using Pythagoras theorem:

Hence, length of diagonal DB is 34 cm.
Solution 14
Let ABCD be the given rhombus whose diagonals intersect at O.
Then AC = 24 cm and BD = 10 cm
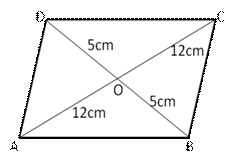
We know that the diagonals of a rhombus bisect each other at right angles.
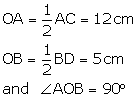
From right ![]() AOB, we have
AOB, we have

Hence, each side of a rhombus 13 cm
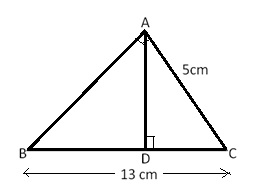
Solution 15
Given: ![]() ABC in which D is the midpoint of BC. AE
ABC in which D is the midpoint of BC. AE ![]() BC and AC > AB.
BC and AC > AB.
Then, BD = CD and ![]() AED = 90o,
AED = 90o,
Then, ![]() ADE < 90o and
ADE < 90o and ![]() ADC > 90o
ADC > 90o
In ![]() AED,
AED,

Putting value of ![]() from (1) in (2), we get
from (1) in (2), we get

Solution 16

Solution 17
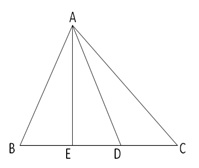
Given: D is the midpoint of side BC, AE ![]() BC, BC = a, AC = b, AB = c, ED = x, AD = p and AE = h
BC, BC = a, AC = b, AB = c, ED = x, AD = p and AE = h
In ![]() AEC,
AEC, ![]() AEC = 90o
AEC = 90o
![]()
(i) In ![]() AEC,
AEC, ![]() AEC = 90o
AEC = 90o
![]()
![]()
![]()
(ii)In ![]() ABE,
ABE, ![]() ABE = 90o
ABE = 90o

(iii)Adding (1) and (2), we get
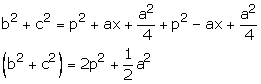
(iv)Subtracting (2) from (1), we get
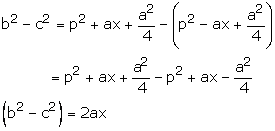
Solution 18
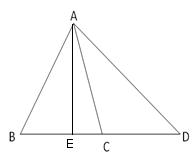
Const: Draw a perpendicular AE from A
Thus, AE ![]() BC
BC
Proof:
In ![]() ABC,AB = AC
ABC,AB = AC
And AE is a bisector of BC
Then,BE = EC
In right angle triangles AED and ACE
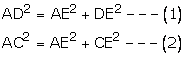
Hence proved.
Solution 19
ABC is an isosceles triangle right angled at B,
Let AB = BC = x cm

By Pythagoras theorem,

Solution 20

Solution 21

(a)


Solution 22


Triangles Exercise Ex. 7E
Solution 1
Two triangles are said to be similar to each other if:
(i) their corresponding angles are equal, and
(ii) their corresponding sides are proportional.
Solution 2
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct point, then the other sides are divided in the same ratio.
Solution 3
If a line divides any two sides of a triangle in the same ratio then the line must be parallel to the third side.
Solution 4
The line segment joining the mid-points of any two sides of a triangle is parallel to the third side.
Solution 5
If in any two triangles, the corresponding angles are equal, then their corresponding sides are proportional and hence the triangles are similar.
Solution 6
If two angles of one triangle are respectively equal to two angles of another triangle then the two triangles are similar.
Solution 7
If the corresponding sides of two triangles are proportional then their corresponding angles are equal, and hence the two triangles are similar.
Solution 8
If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional then the two triangles are similar.
Solution 9
In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Solution 10
In a triangle, if the square of one side is equal to the sum of the squares of the other two sides then the angle opposite to the first side is a right angle.
Solution 11

Solution 12
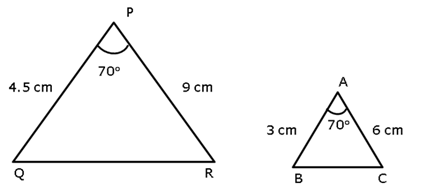

Solution 13
Hence, EF = 12 cm
Solution 14

Solution 15
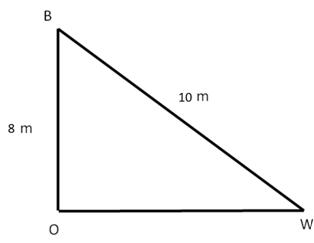

Solution 16


Solution 17
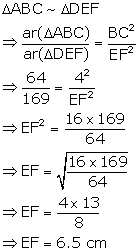
Solution 18
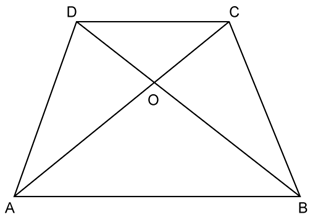

Solution 19
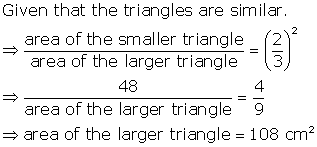
Solution 20
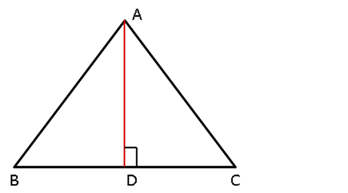
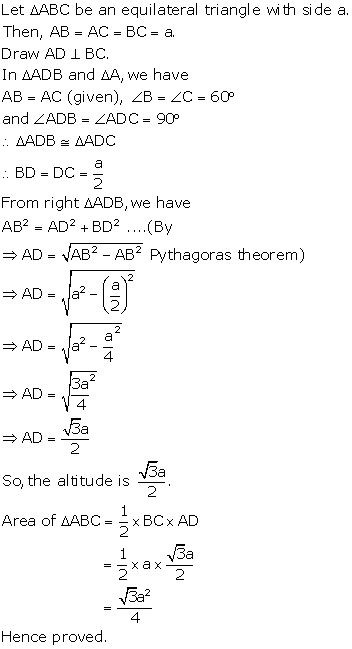
Solution 21
Let
AC = 24 cm
BD = 10 cm

Solution 22

Solution 23

Solution 24
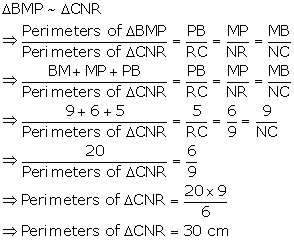
Solution 25


Solution 26
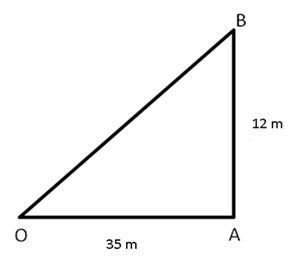

Solution 27
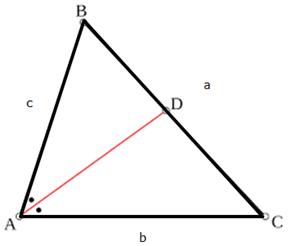

Solution 28
Solution 29


Solution 30 (i)
Similar figures have the same shape but need not have the same size.
Since all circles irrespective of the radii will have the same shape, all will be similar.
So, the statement is true.
Solution 30 (ii)
Two rectangles are similar if their corresponding sides are proportional.
So, the statement is false.
Solution 30 (iii)
Two triangles are said to be similar to each other if:
(i) their corresponding angles are equal, and
(ii) their corresponding sides are proportional.
So, the statement is false.
Solution 30 (iv)
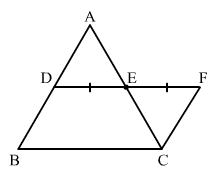

Solution 30 (v)

Solution 30 (vi)
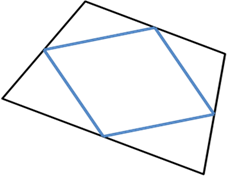
The line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram as shown.
It may or may not be a rhombus.
So, the statement is false.
Solution 30 (vii)

Solution 30 (viii)

Solution 30 (ix)

Solution 30 (x)
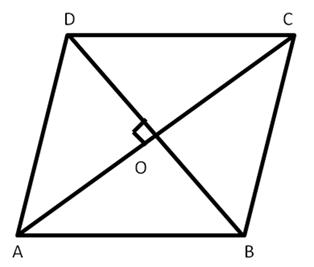

Triangles Exercise MCQ
Solution 1

Solution 2

Solution 3

Solution 4
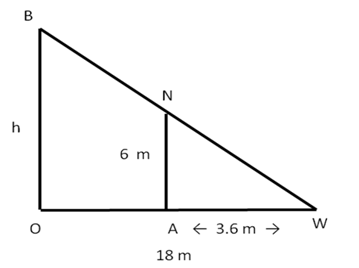

Solution 5
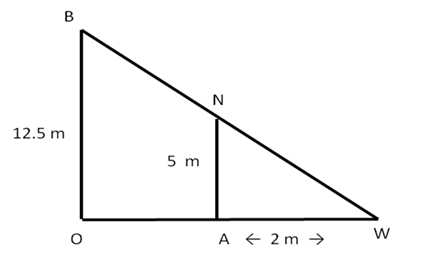

Solution 6
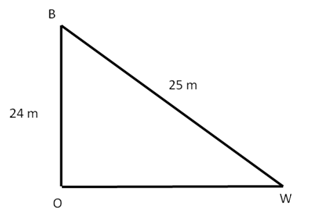
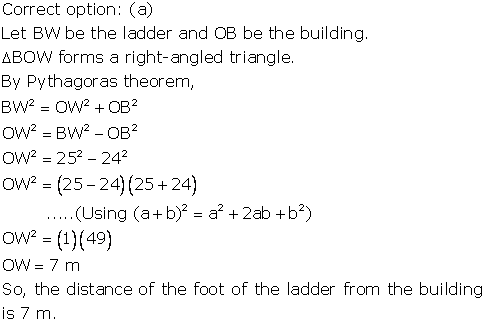
Solution 7

Solution 8

Solution 9


Solution 10
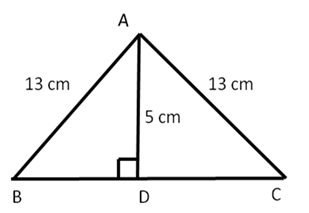

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16
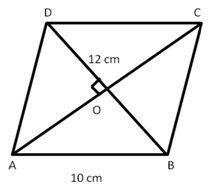

Solution 17
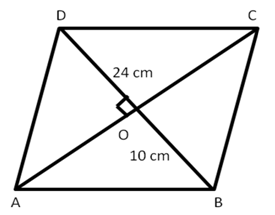

Solution 18
Correct option: (b)
Recall that the diagonals of a trapezium divide each other proportionally.
Note that this happens even in a parallelogram, square and rectangle, but without additional information it is not possible to be sure.
Solution 19

Solution 20
Correct option: (a)
The line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram as shown below.
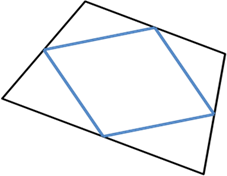
Solution 21
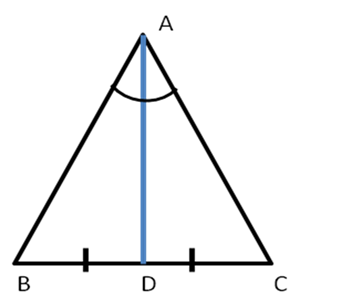

Solution 22
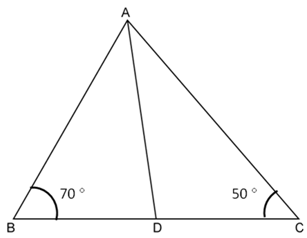

Solution 23

Solution 24

Solution 25

Solution 26

Solution 27

Solution 28

Solution 29

Solution 30
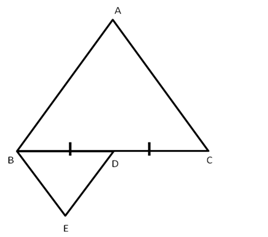

Solution 31

Solution 32

Solution 33

Solution 34
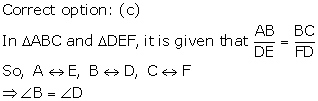
Solution 35
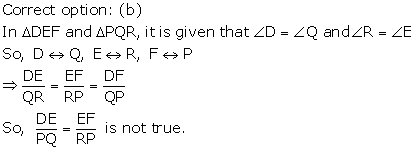
Solution 36

Solution 37
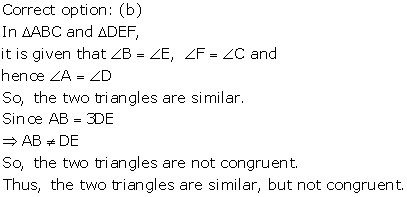
Solution 38

Solution 39

Solution 40

Solution 41

Solution 42


Solution 43

Solution 44

Solution 45

Solution 46
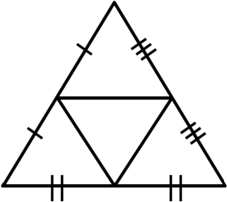
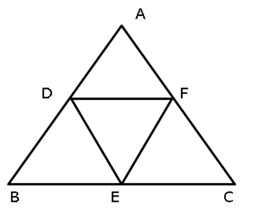
Correct option: (b)
The line segments joining the midpoints of the sides of a triangle form four triangles, each of which is similar to the original triangle.
Solution 47

Solution 48

Solution 49

Solution 50

Solution 51

Solution 52
Correct option: (b)
Clearly, option (b) is false since the ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
Solution 53


Solution 54
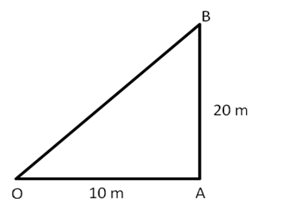


Triangles Exercise Test Yourself
Solution 1

Solution 2

Solution 3
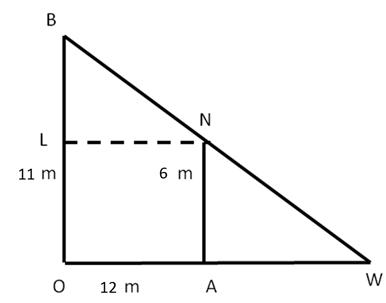

Solution 4

Solution 5
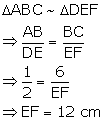
Solution 6

Solution 7
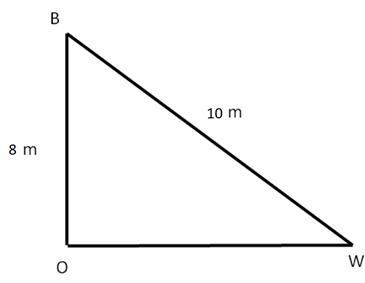

Solution 8


Solution 9

Solution 10
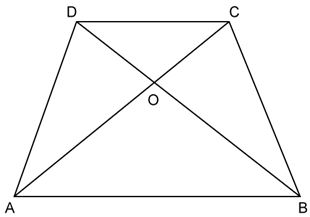

Solution 11
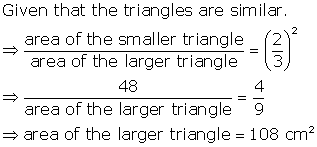
Solution 12

Solution 13


Solution 14
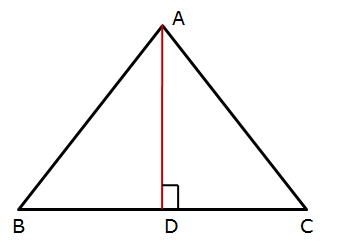
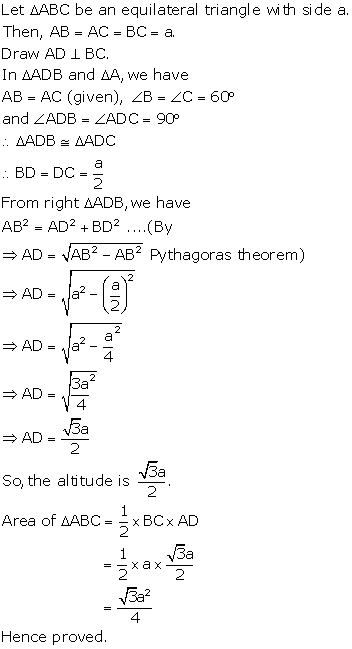
Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20


