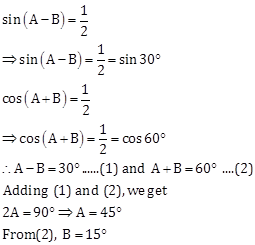Class 10 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 11 - T-Ratios of Some Particular Angles
T-Ratios of Some Particular Angles Exercise Ex. 11
Solution 1
On substituting the value of various T-ratios, we get
sin60o cos30o + cos60o sin30o
Solution 2
sin60° cos30° - cos60° sin30°
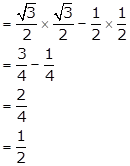
Solution 3
cos60° cos30° - sin60° sin30°
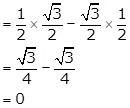
Solution 4
cos45° cos30° + sin45° sin30°
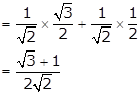
Solution 5
tan30° cosec60° - tan60° sec30°
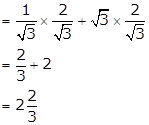
Solution 6
On substituting the value of various Tratios, we get
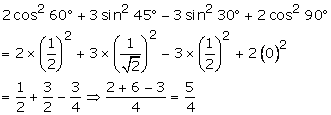
Solution 7
sin230° cos245° + 4 tan230° +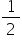 
sin290° + 
cot260°
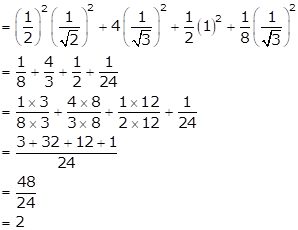
Solution 8
On substituting the value of various Tratios, we get
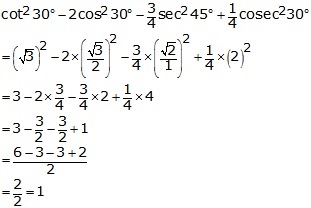
Solution 9
(cos0° + cos45° + sin30°)(sin 90° - cos45° + cos60°)
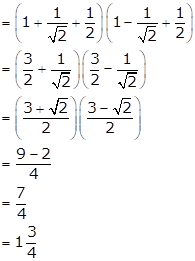
Solution 10
(i)
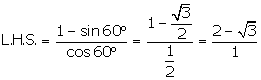
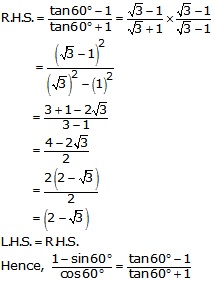
(ii)
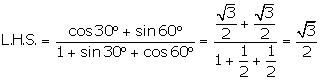
L.H.S = R.H.S.
Solution 11
(i)
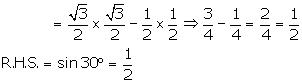
R.H.S. = L.H.S.
Hence, sin60° cos30° - cos60° sin30° = sin30°
(ii)L.H.S. = cos60° cos30° + sin60° sin30°
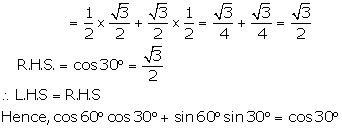
(iii)
R.H.S. = L.H.S.
Hence,2sin30° cos30° = sin60°
(iv)
R.H.S. = sin90° = 1
R.H.S. = L.H.S.
Hence, 2 sin 45° cos45° = sin90°
Solution 12
A = 45° 
2 A = 90°
(i)Sin 2A = sin90° = 1
(ii) cos2A = cos90° = 0
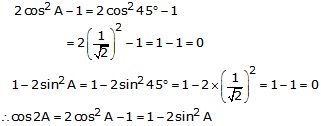
Solution 13
A = 30
2A = 60
(i)
(ii)
(iii)
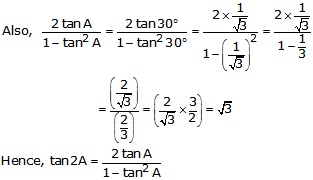
Solution 14(i)
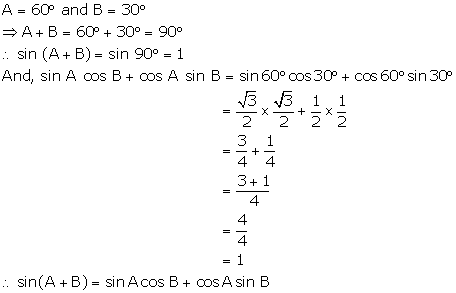
Solution 14(ii)
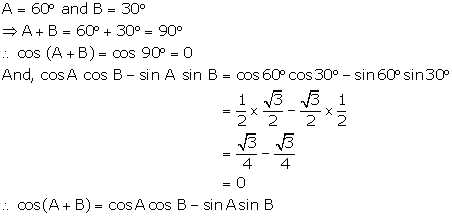
Solution 15(i)
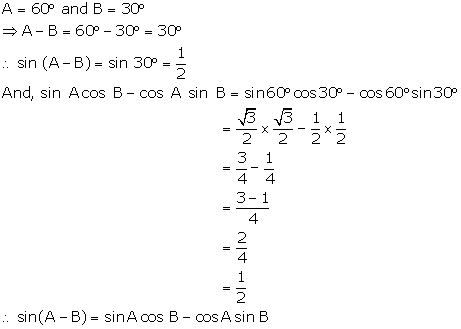
Solution 15(ii)
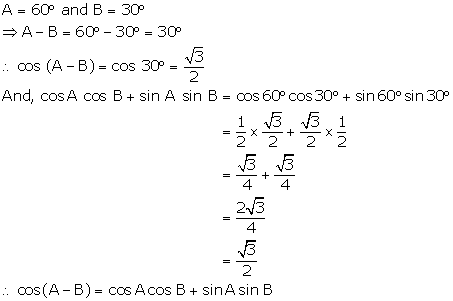
Solution 15(iii)
Solution 16
Hence, (A + B) = 45o
Solution 17
Putting A = 30o 
2 A = 60o
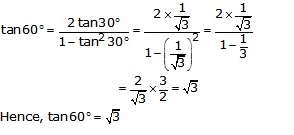
Solution 18
Putting A = 30o 
2 A = 60o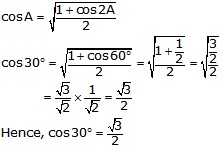
Solution 19
Putting A = 30o 
2 A = 60o
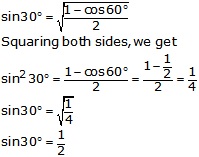
Solution 20
Let A = 45° and B =30°
(i) sin75°
= sin(45°+ 30°)
= sin 45° cos 30° + cos 45° sin 30°
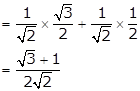
(ii) cos15°
= cos(45°- 30°)
= cos 45° cos 30° + sin 45° sin 30°
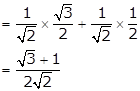
Solution 21
tan(x + 30°) = 1
We know that tan45° = 1
⇒ tan (15° + 30°) = 1
∴ x = 15°
Solution 22
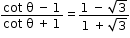
⇒ (1 + √3)(cot θ - 1) = (1 - √3)(cot θ + 1)
⇒ cot θ - 1 + √3 cot θ - √3 = cot θ + 1 - √3 cot θ - √3
⇒ 2√3 cot θ = 2
⇒ cot θ = 1√3 = cot 60°
⇒ θ = 60°
Solution 23
sin(A + B) = 1 = sin90°
⇒ A + B = 90°……(1)
tan(A - B) = 1/√3 = tan 30°
⇒ A - B = 30°…….(2)
Adding (1) and (2), we get
A = 60° and B = 30°
Solution 24
sin(A + B) = √3/2 = sin60°
⇒ A + B = 60°…….(1)
Cos(A - B) = √3/2 = cos30°
⇒ A - B = 30°……(2)
Adding (1) and (2), we get
A = 45° and B = 15°
Solution 25
Solving (1) and (2), we get
2A = 90o
A = 45o
Putting A = 45o in (1), we get
45o - B = 30o B = 45o - 30o = 15o
A = 45o, B = 15o
Solution 26
cosec(A + B) = 1 - cosec90°
⇒ A + B = 90°…….(1)
Cosec(A - B) = 2 = cosec30°
⇒ A - B = 30°…..(2)
Adding (1) and (2), we get
A = 60° and B = 30°
(i) sinA cosB + cosA sinB
= sin60° cos30° + cos60°sin30°
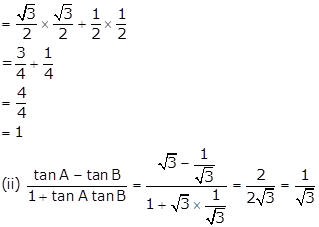
Solution 27
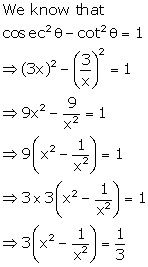
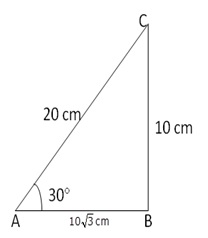
Solution 28
From right angled 
ABC,
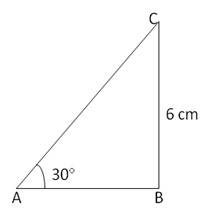
Solution 29
From right angled 
ABC,
Solution 30
From right angled 
ABC,
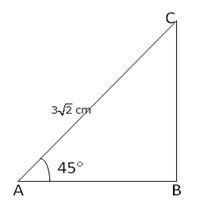
(i)
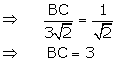
(ii) By Pythagoras theorem
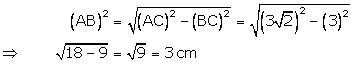
Hence, (i) BC = 3cm and (ii) AB = 3cm
Solution 31
(i) x tan 45° cot60° = sin 30° cosec60°
⇒ x = 1
(ii) 2cosec230° + x sin2 60° - ¾ tan2 30° = 10
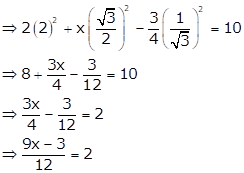
⇒ 9x = 27
⇒ x = 3
T-Ratios of Some Particular Angles Exercise MCQ
Solution 1
Correct Option: (c)
Solution 2
Correct Option: (d)
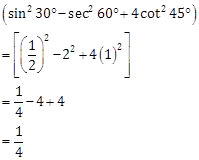
Solution 3
Correct Option: (c)
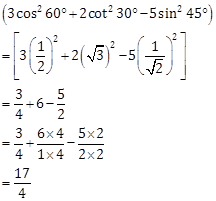
Solution 4
Correct Option: (b)
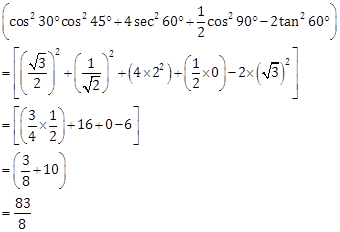
Solution 5
Correct option: (a)
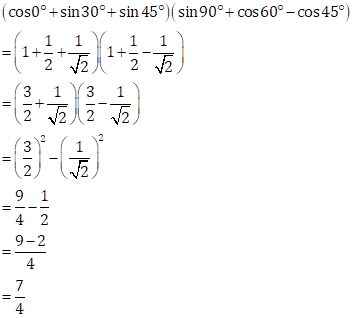
Solution 6
Correct Option: (c)
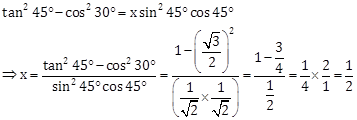
Solution 7
Correct Option: (a)
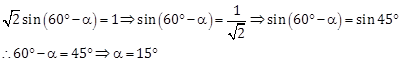
Solution 8
Correct Option: (a)
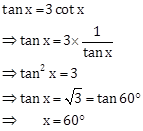
Solution 9
Correct Option: (b)
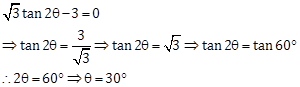
Solution 10
Correct Option: (a)
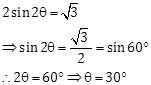
Solution 11
Correct Option: (c)
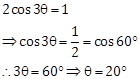
Solution 12
Correct Option: (a)
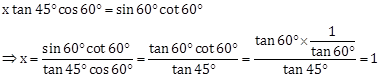
Solution 13
Correct Option: (d)
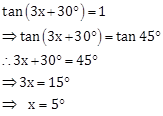
Solution 14
Correct Option: (b)
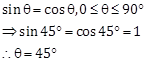
Solution 15
Correct Option: (c)
