Class 10 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 1 - Real Numbers
Real Numbers Exercise Ex. 1A
Solution 1
For any two given positive integers a and b there exist unique whole numbers q and r such that
![]()
Here, we call 'a' as dividend, b as divisor, q as quotient and r as remainder.
Dividend = (divisor ![]() quotient) + remainder
quotient) + remainder
Solution 2
By Euclid's Division algorithm we have:
Dividend = (divisor × quotient) + remainder
= (61 ![]() 27) + 32 = 1647 + 32 = 1679
27) + 32 = 1647 + 32 = 1679
Solution 3
By Euclid's Division Algorithm, we have:
Dividend = (divisor ![]() quotient) + remainder
quotient) + remainder
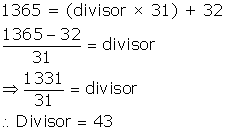
Solution 4(i)
Here, 612 < 1314
Applying Euclid's division algorithm, we get
1314 = 612 × 2 + 90 ….. r ≠ 0
612 = 90 × 6 + 72 ….. r ≠ 0
90 = 72 × 1 + 18 ….. r ≠ 0
72 = 18 × 4 + 0
Since remainder is zero.
Hence, HCF of 612 and 1314 is 18.
Solution 4(ii)
Here, 1260 < 7344
Applying Euclid's division algorithm, we get
7344 = 1260 × 5 + 1044 ….. r ≠ 0
1260 = 1044 × 1 + 216 ….. r ≠ 0
1044 = 216 × 4 + 180 ….. r ≠ 0
216 = 180 × 1 + 36 ….. r ≠ 0
180 = 36 × 5 + 0
Since remainder is zero.
Hence, HCF of 1260 and 7344 is 36.
Solution 4(iii)
Here, 4052 < 12576
Applying Euclid's division algorithm, we get
12576 = 4052 × 3 + 420 ….. r ≠ 0
4052 = 420 × 9 + 272 ….. r ≠ 0
420 = 272 × 1 + 148 ….. r ≠ 0
272 = 148 × 1 + 148 ….. r ≠ 0
148 = 124 × 1 + 24 ….. r ≠ 0
124 = 24 × 5 + 4 ….. r ≠ 0
24 = 4 × 6 + 0
Since remainder is zero.
Hence, HCF of 4052 and 12576 is 4.
Solution 5
Here, 650 < 1170
Applying Euclid's division algorithm, we get
1170 = 650 × 1 + 520 ….. r ≠ 0
650 = 520 × 1 + 130 ….. r ≠ 0
520 = 130 × 4 + 0
Since remainder is zero.
Therefore, HCF of 650 and 1170 is 130.
Hence, the largest number which divides 650 and 1170 is 130.
Solution 6
We know that,
Smallest prime number = 2
Smallest composite number = 4
HCF of 2 and 4 is 2.
Hence, the HCF of the smallest prime number and the smallest composite number is 2.
Solution 7
Any positive integer is of the form 6m, 6m + 1, 6m + 2, 6m + 3, 6m + 4, 6m + 5 for some positive integer n.
When n = 6m,
n3 - n
= (6m)3 - 6m
= 216 m3 - 6m
= 6m(36m2 - 1)
= 6q, where q = m(36m2 -1)
![]() n3 - n is divisible
by 6
n3 - n is divisible
by 6
When n = 6m + 1,
n3 - n
= n(n2 - 1)
= n (n - 1) (n + 1)
= (6m + 1) (6m) (6m + 2)
= 6m(6m + 1) (6m + 2)
= 6q, where q = m(6m + 1) (6m + 2)
∴n3 - n is divisible by 6
When n = 6m + 2,
n3- n
= n (n - 1) (n + 1)
= (6m + 2) (6m + 1) (6m + 3)
= (6m + 1) (36 m2 + 30m + 6)
= 6m (36 m2 + 30m + 6) + 1 (36m2 + 30m + 6)
= 6[m (36m2 + 30m + 6)] + 6 (6m2 + 5m + 1)
= 6p + 6q,
Where p = m (36m2 + 30m + 6)
q = 6m2 + 5m + 1
∴ n3 - n is divisible by 6
When n = 6m + 3
n3 - n
= (6m + 3)3 - (6m + 3)
= (6m + 3) [(6m + 3)2 - 1]
= 6m [6m + 3)2 - 1] + 3 [(6m + 3)2 - 1]
= 6 [m [(6m + 3)2 - 1] + 3 [36m2 + 36m + 8]
= 6 [m [(6m + 3)2 - 1] + 6 [18m2 + 18m + 4]
= 6p + 3q,
Where p = m[(6m + 3)2 - 1]
q = 18m2 + 18m + 4
∴ n3 - n is divisible by 6.
Solution 8
Let the two odd positive no. be x = 2k + 1 and y = 2p + 1
Hence, x2 + y2 = (2k + 1)2 +(2p + 1)2
= 4k2 + 4k + 1 + 4p2 + 4p + 1
= 4k2 + 4p2 + 4k + 4p + 2
= 2(2k2 + 2p2 + 2k + 2p + 1)
Therefore, x2 + y2 = 2m, where m = 2k2 + 2p2 + 2k + 2p + 1.
So, x2 + y2 is an even number.
Also, it does not have any multiple of 4 as a factor, hence
x2 + y2 is even but not divisible by 4.
Solution 9
Her, 1190 < 1445
1445 = 1190 x 1 + 255 ….. r ≠ 0
1190 = 255 x 4 +170 ….. r ≠ 0
255 = 170 x 1 + 85 ….. r ≠ 0
170 = 85 x 2 + 0
Since remainder is zero
Therefore, HCF of 1190 and 1445 is 85.
85 = 255 - 170 x 1
= (1445 - 1190 x 1) - (1190 - 255 x 4)
= (1445 - 1190) - [1190 - (1445 - 1190) x 4]
= (1445 - 1190) - (1190 - 1445 x 4 - 1190 x 4)
= 1445 - 1190 - (1190 x 5 - 1445 x 4)
= 1445 - 1190 - 1190 x 5 + 1445 x 4
= 1445 x 5 - 1190 x 6
= 1190 x (- 6) + 1445 x 5
= 1190m + 1445n, where m= -6 and n = 5
Solution 10
Here, 441< 567
Applying Euclid's division algorithm, we get
567 = 441 × 1 + 126 ….. r ≠ 0
441 = 126 × 3 + 63 ….. r ≠ 0
126 = 63 × 2 + 0
Since remainder is zero.
Therefore, HCF of 441 and 567 is 63. ….(i)
Here, 63 < 693
Applying Euclid's division algorithm, we get
693 = 63 × 11 + 0
Since remainder is zero.
Therefore, HCF of 63 and 693 is 63. ….(ii)
From (i) and (ii),
HCF of 441, 567 and 693 is 63.
Solution 11
1251 - 1 = 1250
9377 - 2 = 9375
15628 - 3 = 15625
Now, we find the HCF of 1250, 9375 and 15625.
Here, 1250 < 9375
Applying Euclid's division algorithm, we get
9375 = 1250 × 7 + 625 ….. r ≠ 0
1250 = 625 × 2 + 0
Since remainder is zero.
Therefore, HCF of 1250 and 9275 is 625.….(i)
Here, 625 < 15625
Applying Euclid's division algorithm, we get
15625 = 625 × 25 + 0
Since remainder is zero.
Therefore, HCF of 625 and 15625 is 625. ….(ii)
From (i) and (ii),
HCF of 1250, 9375 and 15625 is 625.
Hence, the largest number that divides 1251, 9377 and 15628 leaving remainders 1, 2 and 3 respectively is 625.
Real Numbers Exercise Ex. 1B
Solution 1
429 = 3 × 11 × 13
Solution 2
5005 = 5 × 7 × 11 × 13
Solution 3
2431 = 11 × 13 × 17
Solution 4(i)
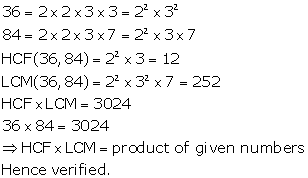
Solution 4(ii)
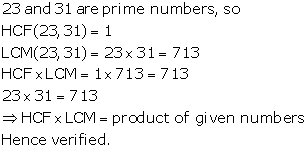
Solution 4(iii)

Hence, verified.
Solution 4(iv)

Solution 4(v)

Solution 4(vi)

Solution 5(i)
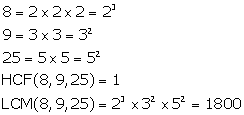
Solution 5(ii)
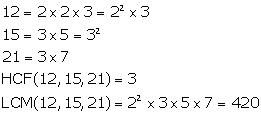
Solution 5(iii)
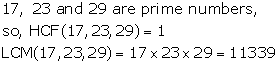
Solution 5(iv)

Solution 5(v)

Solution 5(vi)
21 = 3 × 7
28 = 2 × 2 × 7 = 22 × 7
36 = 2 × 2 × 3 × 3 = 22 × 32
HCF(21, 28, 36) = 1
LCM(21, 28, 36) = 22 × 32 × 7 = 4 × 9 × 7 = 252
Solution 6
Prime factorization of 404 and 96 is given by
404 = 2 × 2 × 101 = 22 × 101
96 = 2 × 2 × 2 × 2 × 2 × 3 = 25 × 3
HCF(404, 96) = 2 × 2 = 4
LCM(404, 96) = 25 × 3 × 101 = 9696
We have,
HCF × LCM = Product of the two numbers
⇒ 4 × 9696 = 404 × 96
⇒ 38784 = 38784
⇒ LHS = RHS
Hence, it is verified.
Solution 7
a = x3y2 = x × x × x × y × y
b = xy3 = x × y × y × y
HCF(a, b) = x × y × y = xy2
LCM(a, b) = x3y3
Solution 8
Solution 9
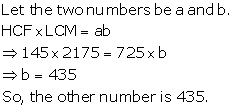
Solution 10
We know that,
Product of the two numbers = HCF × LCM
⇒ ab = 5 × 200
⇒ ab = 1000
Solution 11
Let a and b be two numbers.
According to the condition,
LCM(a, b) = 9 × HCF(a, b) …. (i)
LCM(a, b) + HCF(a, b) = 500 …. (ii)
From (i) and (ii), we get
9 × HCF(a, b) + HCF(a, b) = 500
⇒ 10 HCF(a, b) = 500
⇒ HCF(a, b) = 50
Solution 12
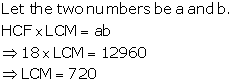
Solution 13
We know that,
LCM = Product of highest power of each factor involved in the numbers.
HCF = Product of smallest power of each common factor
⇒ LCM is always a multiple of HCF.
⇒ LCM = k × HCF
Here, LCM = 175 and HCF = 15
But in this case, LCM ≠ k × HCF.
Therefore, two numbers can't have LCM as 175 and HCF as 15.
Solution 14(i)
![]()
Solution 14(ii)
![]()
Solution 14(iii)
![]()
Solution 14(iv)
![]()
Solution 15
Clearly, the required number divides 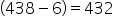 and
and 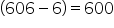 exactly.
exactly.
Therefore, required number = HCF(432, 600).
Now,

Hence, 24 is the required number.
Solution 16
Subtracting 5 and 7 from 320 and 457 respectively:
320 - 5 = 315,
457 - 7 = 450
Let us now find the HCF of 315 and 405 through prime factorization:
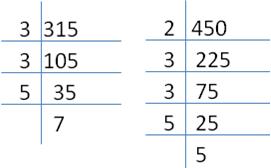

![]()
![]() The required number is 45.
The required number is 45.
Solution 17
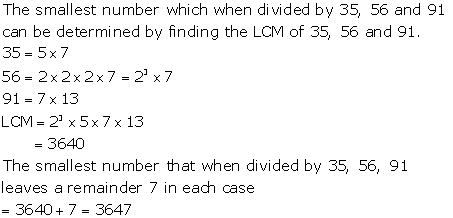
Solution 18

Solution 19

Solution 20

Solution 21
Largest four-digit number = 9999
Now,
4 = 2 × 2
7 = 7 × 1
13 = 13 × 1
Therefore, LCM (4, 7, 13) = 2 × 2 × 7 × 13 = 364
On dividing 9999 by 364, the remainder = 171
That means, 9999 - 171 = 9828 is exactly divided by 4, 7 and 13.
And, largest four-digit number leaving remainder 3 when divided by 4, 7 and 13 = 9828 + 3 = 9831
Solution 22
5 = 5 × 1
6 = 2 × 3
4 = 2 × 2
3 = 3 × 1
Therefore, LCM(5, 6, 4, 3) = 5 × 2 × 2 × 3 = 60
On dividing 2497 by 60, the remainder = 37
Hence, number to be added = 60 - 37 = 23
Solution 23
Difference between 43 and 91 = 91 - 43 = 48
Difference between 91 and 183 = 183 - 91 = 92
Difference between 183 and 43 = 183 - 43 = 140
Now,
48 = 2 × 2 × 2 × 2 × 3
92 = 2 × 2 × 23
140 = 2 × 2 × 5 × 7
Now, HCF (48, 92, 140) = 2 × 2 = 4
Hence, 4 is the greatest number that will divide 43, 91 and 183 leaving the same remainder.
Solution 24
Now,
20 - 14 = 6
25 - 19 = 6
35 - 29 = 6
40 - 34 = 6
And,
20 = 2 × 2 × 5 = 22 × 5
25 = 5 × 5 = 52
35 = 5 × 7
40 = 2 × 2 × 2 × 5 = 23 × 5
Therefore, LCM (20, 25, 35, 40) = 23 × 52 × 7 = 1400
Hence, required number = 1400 - 6 = 1394
Solution 25

Solution 26
Let us find the HCF of 336, 240 and 96 through prime factorization:
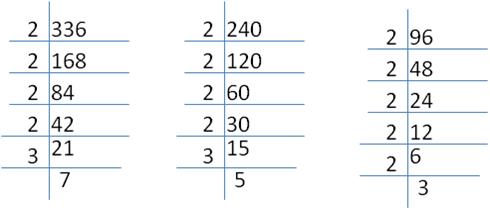
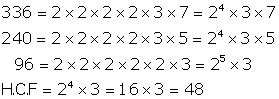
Each stack of book will contain 48 books
Number of stacks of the same height
![]()
Solution 27
The prime factorization of 42, 49 and 63 are
42 = 2 × 3 × 7
49 = 7 × 7
63 = 3 × 3 × 7
⇒ HCF(42, 49, 63) = 7
Hence, greatest possible length of each plank is 7m.
We have total length of timber = 42 + 49 + 63 = 154
Number of planks = 154/7 = 22
Therefore, 22 planks were formed.
Solution 28
7 m = 700cm, 3m 85cm = 385 cm
12 m 95 cm = 1295 cm
Let us find the prime factorization of 700, 385 and 1295:
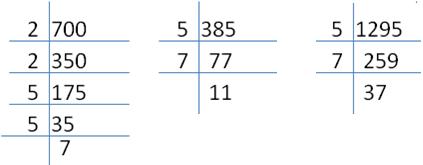

Greatest possible length = 35cm
Solution 29
Let us find the prime factorization of 1001 and 910:
1001 = 11 ![]() 7
7 ![]() 13
13
910 = 2 ![]() 5
5 ![]() 7
7 ![]() 13
13

H.C.F. of 1001 and 910 is 7 ![]() 13 = 91
13 = 91
Maximum number of students = 91
Solution 30

Solution 31
Let us find the LCM of 64, 80 and 96 through prime factorization:

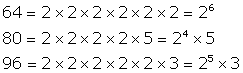
L.C.M of 64, 80 and 96
= ![]()
Therefore, the least length of the cloth that can be measured an exact number of times by the rods of 64cm, 80cm and 96cm = 9.6m
Solution 32
Interval of beeping together = LCM (60 seconds, 62 seconds)
The prime factorization of 60 and 62:
60 = 30 ![]() 2, 62 = 31
2, 62 = 31 ![]() 2
2
![]() L.C.M of 60 and 62 is 30 31
L.C.M of 60 and 62 is 30 31 ![]() 2 = 1860 sec = 31min
2 = 1860 sec = 31min
![]() electronic device will beep after every 31minutes
electronic device will beep after every 31minutes
After 10 a.m., it will beep at 10 hrs 31 minutes
Solution 33
Therefore, all three lights will again change simultaneously after 7 min 12 sec, that is at 8:7:12 hours.
Solution 34
Solution 35
![]()
Now, a number ending with 0 should have 5 as factor.
But, 5 is not a factor of 6n.
Hence, 6n can never end with 0 for any natural number n.
Real Numbers Exercise Ex. 1C
Solution 1(i)
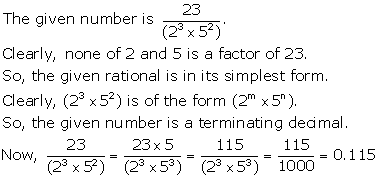
Solution 1(ii)

Solution 1(iii)

Solution 1(iv)

Solution 1(v)

Solution 1(vi)

Solution 2(i)
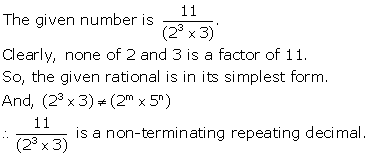
Solution 2(ii)
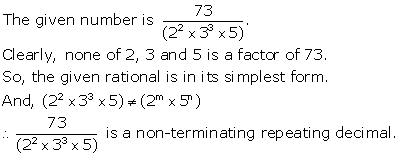
Solution 2(iii)
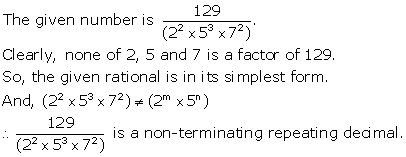
Solution 2(iv)

Solution 2(v)

Solution 2(vi)

Solution 2(vii)

Solution 2(viii)

Solution 3
Real Numbers Exercise Ex. 1D
Solution 1
Rational Numbers:
The numbers of the form  , where
, where 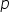 and
and 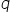 are integers and
are integers and 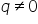 , are called rational numbers.
, are called rational numbers.
Irrational numbers:
The numbers that are expressible as non-terminating and non-repeating decimals when expressed in decimal form are known as irrational numbers.
Real numbers:
Rational numbers and irrational numbers together form a set of real numbers.
Solution 2
Solution 3
√2 = 1.414….and √3 = 1.732…
We know that, 1.414 < 1.5 < 1.732
Therefore a rational number between √2 and √3 is 1.5.
Solution 4
Proof:
Let us assume that √6 is a rational number.
![]() , where a and
b are integers having no common factor other than 1, and b ≠ 0.
, where a and
b are integers having no common factor other than 1, and b ≠ 0.
Now, ![]() ….(
on squaring both sides)
….(
on squaring both sides)
⇒ 6b2 = a2 ……(1)
⇒ 6 divides a2 ….. (∵ 6 divides 6b2)
⇒ 6 divides a
Let a = 6c for some integer c
Putting a = 6c in (1), we get
6b2 = 36c2
⇒ b2 = 6c2
⇒ 6 divides b2 ….. (∵ 6 divides 6c2)
⇒ 6 divides b ….. (∵ 6 divides b2 = 6 divides b)
Thus, 6 is a common factor of a and b
But, this contradicts the fact that a and b have no common factor other than 1.
The contradiction arises by assuming that √6 is rational.
Hence, √6 is irrational.
Solution 5
If possible (2 + √3) is rational.
⇒ (2 + √3) - 2 is rational…. (∵ difference of two rationals is rational)
Therefore, √3 is rational.
This contradicts the fact √3 is irrational.
Since the contradiction arises by assuming (2 + √3) rational.
Hence, (2 + √3) is irrational.
Solution 6
If possible (4 - √3) is rational.
⇒ 4 -(4 - √3) is rational….(∵ difference of two rationals is rational)
Therefore, √3 is rational.
This contradicts the fact √3 is irrational.
Since the contradiction arises by assuming (4 - √3) rational.
Hence, (4 - √3) is irrational.
Solution 7
If possible (3 + 5√2) is rational.
Now, (3 + 5√2) - 3 = 5√2 is rational (∵ difference of two rationals is rational)
Also, ![]() ×
5√2 = √2 is rational (∵
Product of two rationals is rational)
×
5√2 = √2 is rational (∵
Product of two rationals is rational)
Therefore, √2 is rational.
This contradicts the fact √2 is irrational.
Since the contradiction arises by assuming (3 + 5√2) rational.
Hence, (3 + 5√2) is irrational.
Solution 8
If possible (2 + 3√5) is rational.
Now, (2 + 3√5) - 2 = 3√5 is rational (∵ difference of two rationals is rational)
Also, ![]() ×
3√5 = √5) is rational (∵
Product of two rationals is rational)
×
3√5 = √5) is rational (∵
Product of two rationals is rational)
Therefore, √5 is rational.
This contradicts the fact √5 is irrational.
Since the contradiction arises by assuming (2 + 3√5) rational.
Hence, (2 + 3√5) is irrational.
Solution 9
If possible ![]() is
rational.
is
rational.
Now,![]() (∵ difference of two
rationals is rational)
(∵ difference of two
rationals is rational)
Also, ![]() (∵
Product of two rationals is rational)
(∵
Product of two rationals is rational)
Therefore, √2 is rational.
This contradicts the fact √2 is irrational.
Since the
contradiction arises by assuming ![]() rational.
rational.
Hence, ![]() is
irrational.
is
irrational.
Solution 10

Solution 11

Solution 12
Solution 13

Solution 14
![]()
Let us assume that ![]() from 1 is
a rational number.
from 1 is
a rational number.
![]() ,
where a and b are non - zero integers having no common factor other than 1,
and b ≠ 0.
,
where a and b are non - zero integers having no common factor other than 1,
and b ≠ 0.
Now, ![]()
But, 5a and 3b are non - zero integers.
![]() is
rational.
is
rational.
Thus, from (2), it follows that √5 is rational.
This contradicts the fact that √5 is irrational.
The contradiction
arises by assuming that ![]() is
rational.
is
rational.
Hence, ![]() is
irrational.
is
irrational.
Solution 15
Let ![]() be rational.
be rational.
Then, there exist
co-primes ![]() and
and ![]() such that
such that

Since ![]() and
and ![]() are integers, so
are integers, so ![]() is rational.
is rational.
But, ![]() is irrational.
is irrational.
Thus, we arrive at a contradiction.
Since the contradiction arises by assuming that ![]() is rational, hence,
is rational, hence, ![]() is irrational.
is irrational.
Solution 16
Solution 17
(i) The sum of two rationals is always rational - True
(ii) The product of two rationals is always rational - True
(iii) The sum of two irrationals is always an irrational - False
(iv) The product of two irrationals is always an irrational - False
(v) The sum of a rational and an irrational is irrational - True
(vi) The product of a rational and an irrational is irrational - True
Real Numbers Exercise Ex. 1E
Solution 1
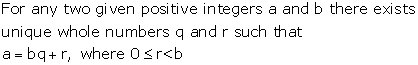
Solution 2

Solution 3
![]()
Solution 4
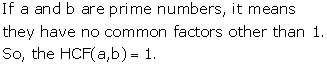
Solution 5
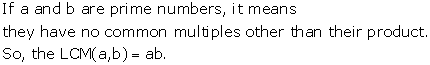
Solution 6
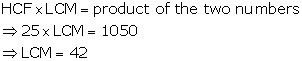
Solution 7
A whole number that can be divided evenly by numbers other than 1 or itself.
Solution 8
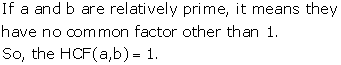
Solution 9

Solution 10

Solution 11

Solution 12
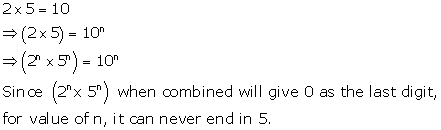
Solution 13

Solution 14
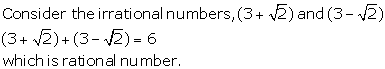
Solution 15

Solution 16

Solution 17
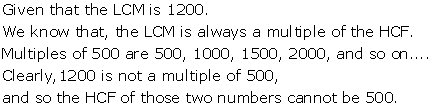
Solution 18

Solution 19

Solution 20

Solution 21

Solution 22
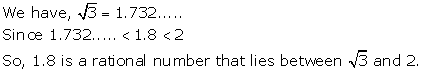
Solution 23

Real Numbers Exercise MCQ
Solution 1

Solution 2
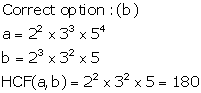
Solution 3
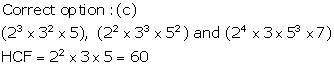
Solution 4
Correct option: (d)
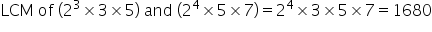
Solution 5

Solution 6
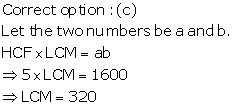
Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 16

Solution 17
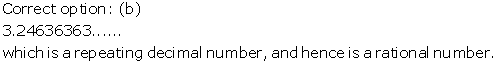
Solution 18

Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26

Real Numbers Exercise Test Yourself
Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7
A number is a terminating deicmal, if its denominator is of the form 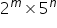 , where
, where  and
and 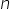 are non-negative integers.
are non-negative integers.
Now,
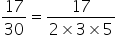
Since the denominator of 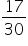 is not of the form
is not of the form 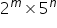 as it has an additional factor
as it has an additional factor 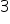 also.
also.
Therefore, 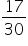 is not a terminating decimal.
is not a terminating decimal.
Solution 8
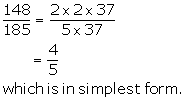
Solution 9

Solution 10
If possible (4 + 3√5) is rational.
Now, (4 + 3√5) - 4 = 3√5 is rational (∵ difference of two rationals is rational)
Also, ![]() × 3√5 = √ is rational. (∵ Product of two rationals is rational)
× 3√5 = √ is rational. (∵ Product of two rationals is rational)
Therefore, √5 is rational.
This contradicts the fact √5 is irrational.
Since the contradiction arises by assuming (4 + 3√5) rational.
Hence, (4 + 3√5) is irrational.
Solution 11

Solution 12
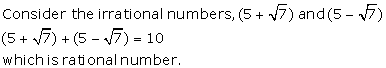
Solution 13
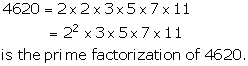
Solution 14
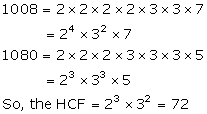
Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20


