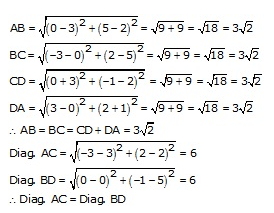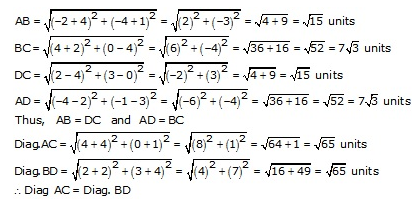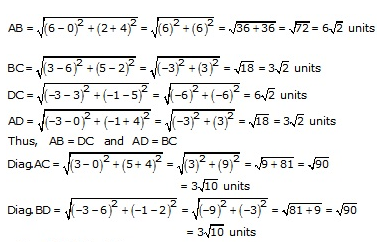Class 10 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 6 - Co-ordinate Geometry
Co-ordinate Geometry Exercise Ex. 6A
Solution 1
(i)The given points are A(9,3) and B(15,11)

(ii)The given points are A(7,4) and B(-5,1)

(iii)The given points are A(-6, -4) and B(9,-12)

(iv)The given points are A(1, -3) and B(4, -6)

(v)The given points are P(a + b, a - b) and Q(a - b, a + b)
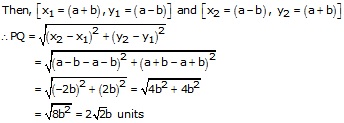
(vi)The given points are P(a sin a, a cos a) and Q(a cos a, - a sina)

Solution 2
(i)The given point is A(5, -12) and let O(0,0) be the origin

(ii)The given point is B(-5, 5) and let O(0,0) be the origin
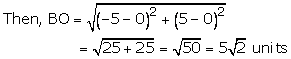
(iii)The given point is C(-4, -6) and let O(0,0) be the origin
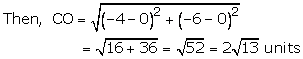
Solution 3
The given points are A(x, -1) and B(5,3)

Solution 4
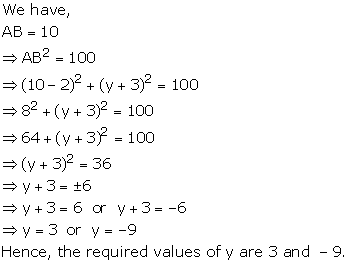
Solution 5
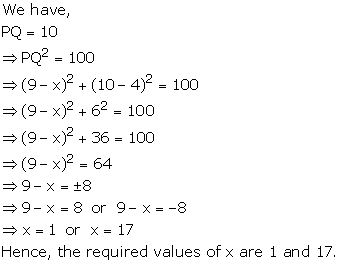
Solution 6
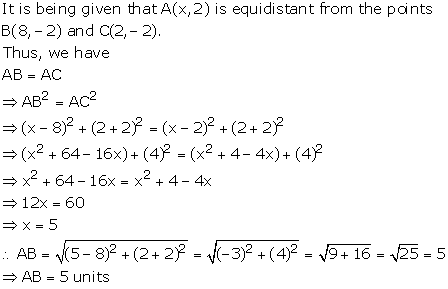
Solution 7
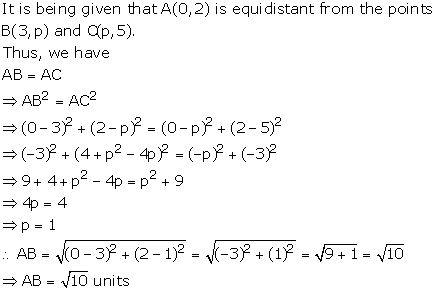
Solution 8
We know that a point on x-axis is of the form (x, 0).
Let A(x, 0) be the point equidistant from P(-2, 5) and Q(2, -3).
Then,
PA = PB
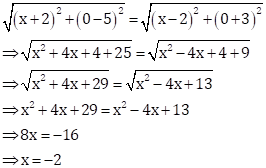
Hence, the required point is (-2, 0).
Solution 9
Let A(11, -8) be the given point and let P(x,0) be the required point on x - axis
Then,

Hence, the required points are (17,0) and (5,0)
Solution 10
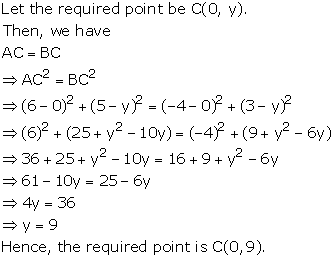
Solution 11

Solution 12
Let A(6, -1) and B(2,3) be the given point and P(x,y) be the required point, we get
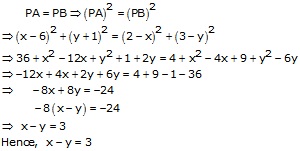
Solution 13
Let the required points be P(x,y), then
PA = PB = PC. The points A, B, C are (5,3), (5, -5) and (1, -5) respectively
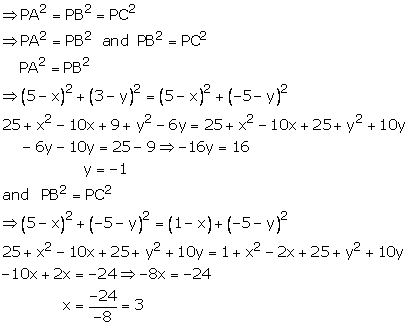
Hence, the point P is (3, -1)
Solution 14

Solution 15
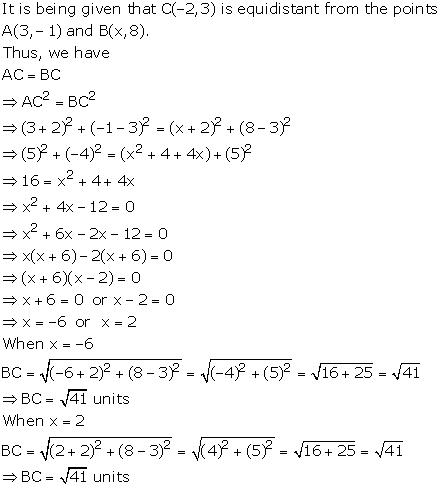
Solution 16
6A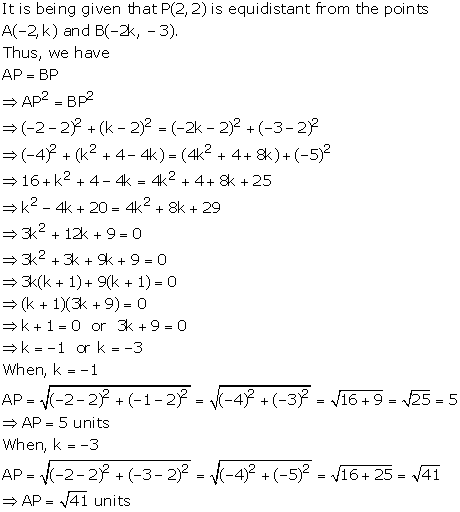
Solution 17

Solution 18(i)

Solution 18(ii)
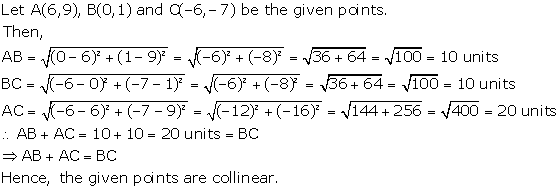
Solution 18(iii)
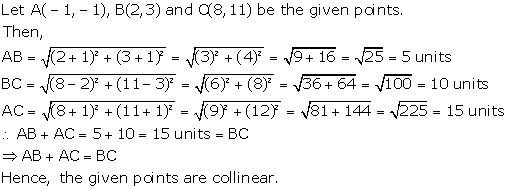
Solution 18(iv)
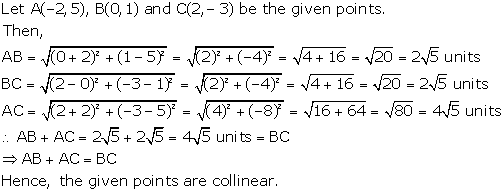
Solution 19

Solution 20
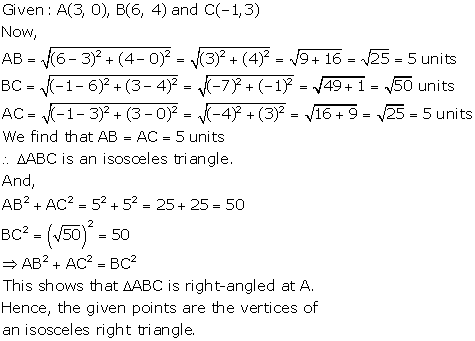
Solution 21
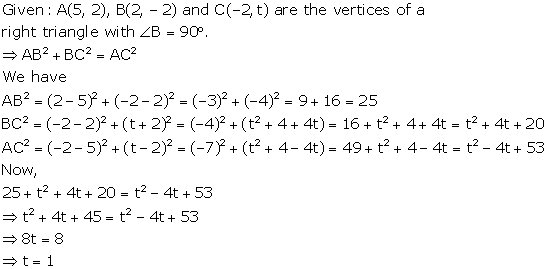
Solution 22
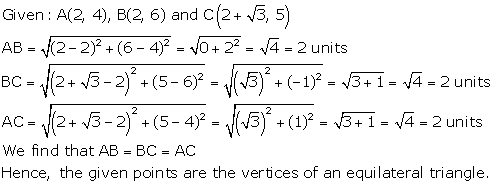
Solution 23
Let ![]() be the given
points.
be the given
points.
Now,
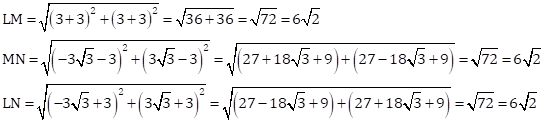 So, we
have
So, we
have
LM = MN = LN
Hence, the triangle LMN formed by the given points is an equilateral triangle.
Solution 24
Let A(-5,6), B(3,0) and C(9,8) be the given points. Then
Solution 25
![]() are the given points
are the given points

Hence, DABC is equilateral and each of its sides being ![]()
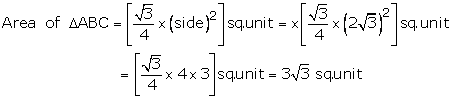
Solution 26
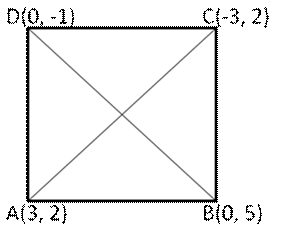
(i)The angular points of quadrilateral ABCD are A(3,2), B(0,5), C(-3,2) and D(0,-1)
Thus, all sides of quad. ABCD are equal and diagonals are also equal
Quad. ABCD is a square
(ii)Let A(6,2), B(2,1), C(1,5) and D(5,6) be the angular points of quad. ABCD. Join AC and BD

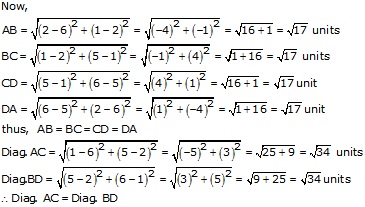
Thus, ABCD is a quadrilateral in which all sides are equal and the diagonals are equal.
Hence, quad ABCD is a square.
(iii)Let A(0, -2), B(3,1), C(0,4) and D(-3,1) be the angular points of quad. ABCD
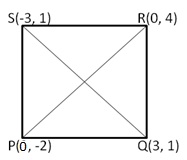
Join PR and QSD
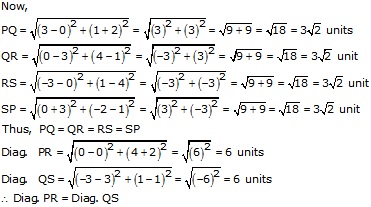
Thus, PQRS is a quadrilateral in which all sides are equal and the diagonals are equal
Hence, quad. PQRS is a square
Solution 27
Let A(-3,2), B(-5, -5), C(2, -3) and D(4,4) be the angular point of quad ABCD. Join AC and BD.
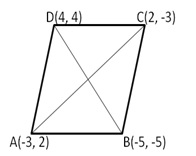

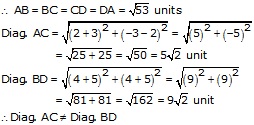
Thus, ABCD is a quadrilateral having all sides equal but diagonals are unequal.
Hence, ABCD is a rhombus
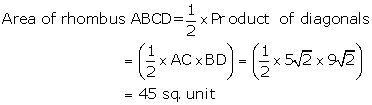
Solution 28
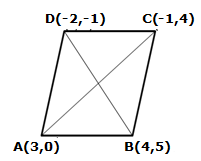

Solution 29
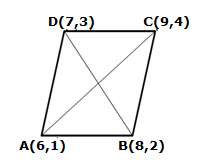

Solution 30
Let A(2,1), B(5,2), C(6,4) and D(3,3) are the angular points of a parallelogram ABCD. Then
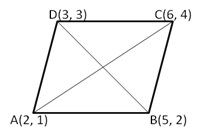

Diagonal AC ![]() Diagonal BD
Diagonal BD
Thus ABCD is not a rectangle but it is a parallelogram because its opposite sides are equal and diagonals are not equal
Solution 31

Solution 32
(i) Let A(-4, -1), B(-2, -4), C(4, 0) and D(2, 3) are the vertices of quad. ABCD. Then
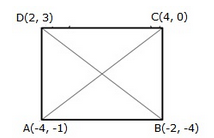
Thus, ABCD is a quadrilateral whose opposite sides are equal and the diagonals are equal
Hence, quad. ABCD is a rectangle.
(ii)Let A(2, -2), B(14, 10), C(11, 13) and D(-1, 1) be the angular points of quad. ABCD, then

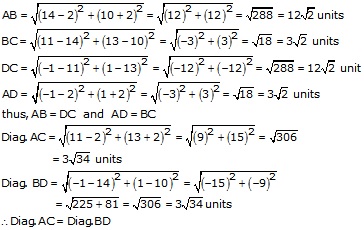
Thus, ABCD is a quadrilateral whose opposite sides are equal and diagonals are equal.
Hence, quad. ABCD is rectangle.
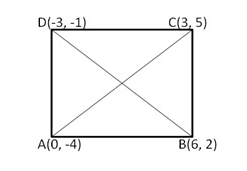
(iii)Let A(0, -4), B(6,2), C(3,5) and D(-3,-1) are the vertices of quad. ABCD. Then
Thus, ABCD is a quadrilateral whose opposite sides are equal and the diagonals are equal
Hence, quad. ABCD is a rectangle
Co-ordinate Geometry Exercise Ex. 6B
Solution 1
(i) The end points of AB are A(-1,7) and B(4, -3)
![]()

Let the required point be P(x, y)
By section formula, we have
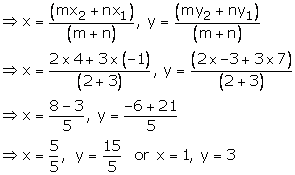
Hence the required point is P(1, 3)
(ii)The end points of PQ are P(-5, 11) and Q(4, -7)
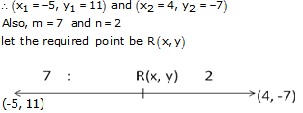
By section formula, we have
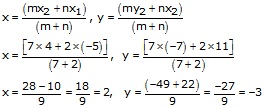
Hence the required point is (2, -3)
Solution 3

Solution 4

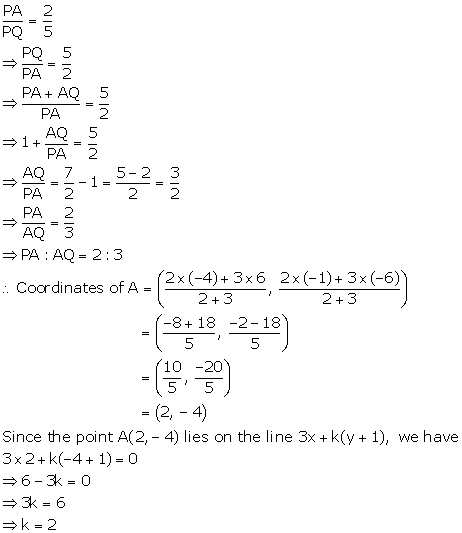
Solution 5
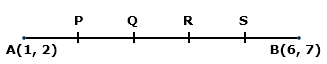

Solution 6
Points P, Q, R divide the line segment joining the points A(1,6) and B(5, -2) into four equal parts
![]() Point P divide AB in the ratio 1 : 3 where A(1, 6), B(5, -2)
Point P divide AB in the ratio 1 : 3 where A(1, 6), B(5, -2)
![]()
Therefore, the point P is
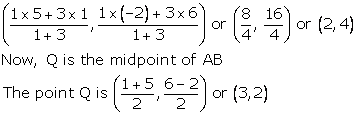
Also, R is the midpoint of the line segment joining Q(3, 2) and B(5, -2)
![]()
Solution 7
Point P divides the join of A(3, -4) and B(1,2) in the ratio 1 : 2.
Coordinates of P are:

Solution 8
(i)The coordinates of mid - points of the line segment joining A(3, 0) and B(-5, 4) are ![]()
(ii)Let M(x, y) be the mid - point of AB, where A is (-11, -8) and B is (8, -2). Then,
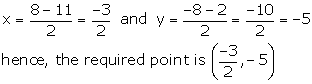
Solution 9
The midpoint of line segment joining the points A(6, -5) and B(-2, 11) is
![]()
Also, given the midpoint of AB is (2, p)
![]() p = 3
p = 3
Solution 10
C(1, 2a + 1) is the midpoint of A(2a, 4) and B(-2, 3b)
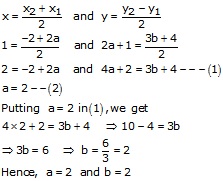
Solution 11
Let A(-2, 9) and B(6, 3) be the two points of the given diameter AB and let C(a, b) be the center of the circle
Then, clearly C is the midpoint of AB
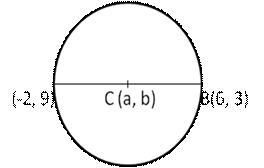
By the midpoint formula of the co-ordinates,
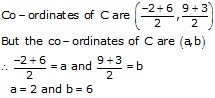
Hence, the required point C(2, 6)
Solution 12
A, B are the end points of a diameter. Let the coordinates of A be (x, y)
The point B is (1, 4)
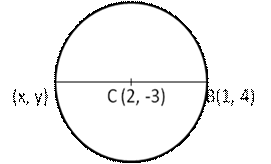
The center C(2, -3) is the midpoint of AB
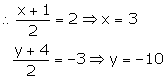
The point A is (3, -10)
Solution 13
Let P divided the join of A(8, 2), B(-6, 9) in the ratio k : 1
By section formula, the coordinates of p are

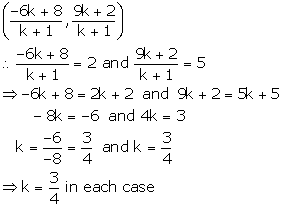
Hence, the required ratio of ![]() which is (3 : 4)
which is (3 : 4)
Solution 14

Solution 15
Let P divided the join of line segment A(-4, 3) and B(2, 8) in the ratio k : 1
![]() the point P is
the point P is

Solution 16
Let P is dividing the given segment joining A(-5, -4) and B(-2, 3) in the ratio r : 1

![]() Coordinates of point P
Coordinates of point P
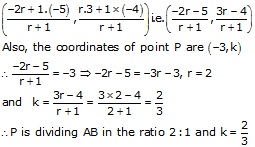
Solution 17
Let the x- axis cut the join of A(2, -3) and B(5, 6) in the ratio k : 1 at the point P
Then, by the section formula, the coordinates of P are ![]()
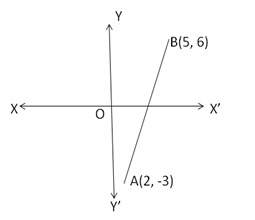
But P lies on the x axis so, its ordinate must be 0
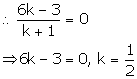
So the required ratio is 1 : 2
Thus the x - axis divides AB in the ratio 1 : 2
Putting ![]() we get the point P as
we get the point P as
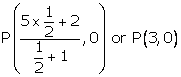
Thus, P is (3, 0) and k = 1 : 2
Solution 18
Let the y - axis cut the join A(-2, -3) and B(3, 7) at the point P in the ratio k : 1
Then, by section formula, the co-ordinates of P are
![]()
But P lies on the y-axis so, its abscissa is 0
![]()
So the required ratio is ![]() which is 2 : 3
which is 2 : 3
Putting ![]() we get the point P as
we get the point P as
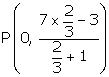 i.e., P(0, 1)
i.e., P(0, 1)
Hence the point of intersection of AB and the y - axis is P(0, 1) and P divides AB in the ratio 2 : 3
Solution 19
Let the line segment joining A(3, -1) and B(8, 9) is divided by x - y - 2 = 0 in ratio k : 1 at p
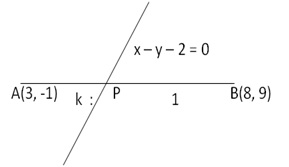
![]() Coordinates of P are
Coordinates of P are
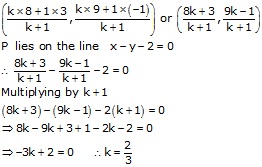
Thus the line x - y - 2 = 0 dividesAB in the ratio 2 : 3
Solution 20
Let D, E, F be the midpoint of the side BC, CA and AB respectively in ![]() ABC
ABC
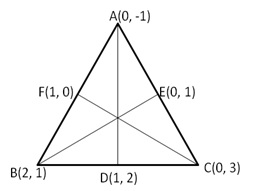
Then, by the midpoint formula, we have

Hence the lengths of medians AD, BE and CF are given by

Solution 21
Here ![]()
Let G(x, y) be the centroid of ![]() ABC, then
ABC, then
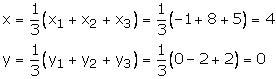
Hence the centroid of ![]() ABC is G(4, 0)
ABC is G(4, 0)
Solution 22
Two vertices of ![]() ABC are A(1, -6) and B(-5, 2) let the third vertex be C(a, b)
ABC are A(1, -6) and B(-5, 2) let the third vertex be C(a, b)
Then, the co-ordinates of its centroid are
![]()
But given that the centroid is G(-2, 1)
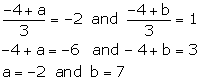
Hence, the third vertex C of ![]() ABC is (-2, 7)
ABC is (-2, 7)
Solution 23
Two vertices of ![]() ABC are B(-3, 1) and C(0, -2) and third vertex be A(a, b)
ABC are B(-3, 1) and C(0, -2) and third vertex be A(a, b)
Then the coordinates of its centroid are

Hence the third vertices A of ![]() ABC is A(3, 1)
ABC is A(3, 1)
Solution 24
Let A(3,1), B(0, -2), C(1, 1) and D(4, 4) be the vertices of quadrilateral
Join AC, BD. AC and BD, intersect other at the point O.
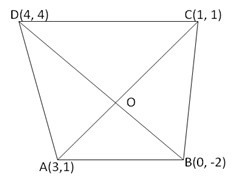
We know that the diagonals of a parallelogram bisect each other
Therefore, O is midpoint of AC as well as that of BD
Now midpoint of AC is ![]()
And midpoint of BD is ![]()
Mid point of AC is the same as midpoint of BD
Hence, A, B, C, D are the vertices of a parallelogram ABCD
Solution 25
Let P(a, -11), Q(5, b), R(2, 15) and S(1, 1) are the vertices of a parallelogram PQRS.
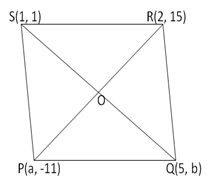
Join the diagonals PR and SQ.
They intersect each other at the point O. We know that the diagonals of a parallelogram bisect each other.
Therefore, O is the midpoint of PR as well as that of SQ
Now, midpoint of PR is ![]()
And midpoint of SQ is ![]()
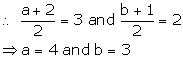
Hence the required values are a = 4 and b = 3
Solution 26
Let A(1, -2), B(3, 6) and C(5, 10) are the given vertices of the parallelogram ABCD
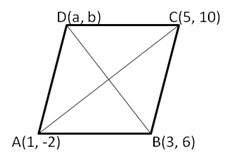
Let D(a, b) be its fourth vertex. Join AC and BD.
Let AC and BD intersect at the point O.
We know that the diagonals of a parallelogram bisect each other.
So, O is the midpoint AC as well as that of BD
Midpoint of AC is ![]()
Midpoint of BD is ![]()

Hence the fourth vertices is D(3, 2)
Solution 27
Solution 28

Solution 29
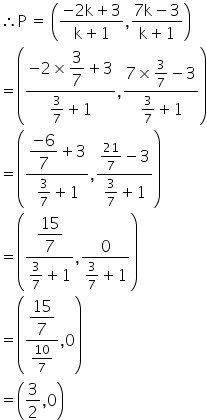
Solution 30
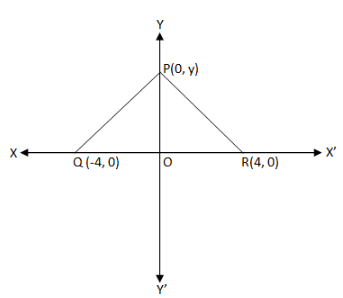

Solution 31
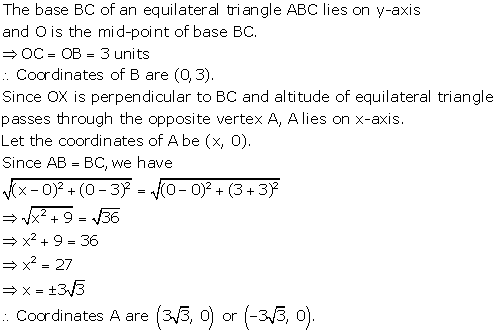
Now, O will be the midpoint of AD
Let (t,0) be the co-ordinates of D
Hence,
AO = OD
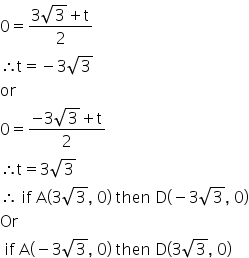
Note: The textbook solution is incorrect
Solution 32

Solution 33
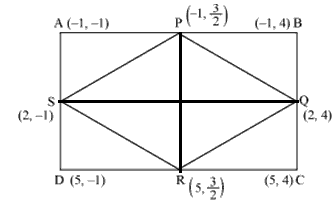

Solution 34

Solution 35
A line intersects the y-axis at point P.
∴ Coordinates of P are.(0,y).
Also, the same line intersects the x-axis at point Q.
∴ Coordinates of Q are.(x,0).
Let S be the midpoint of PQ.
∴ Coordinates of S are.(2,-5)
Now,
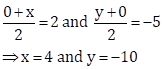
Therefore, coordinates of P are (0,-10) and coordinates of Q are (4,0).
Solution 36
Let the point R divides PQ
in the ratio ![]() .
.
Then, the
coordinates of point R are ![]()
But, the
coordinates of R are given as ![]() .
.
![]()
Consider ![]()

Consider ![]()
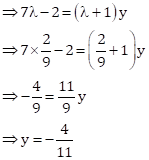
Hence, the point R
divides PQ in the ratio 2:9 and the value of ![]() .
.
Solution 37
Let the coordinates
of vertices A, B and C be ![]() respectively.
respectively.
Given, D(3, 4), E(8, 9) and F(6, 7) are midpoints of the sides BC, CA and AB respectively.
Then, we have
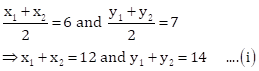

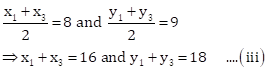
From (i), (ii) and (iii), we have
![]()
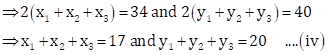
From (i) and (iv),
![]()
From (ii) and (iv),
![]()
From (iii) and (iv),
![]()
Hence, the coordinates of the vertices of triangle ABC are A(11, 12), B(1, 2) and C(5, 6).
Solution 38
Let PQRS be the given paralleogram.
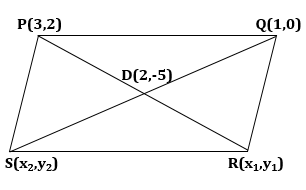
Now, diagonals of a parallleogram bisect each other.
So, we have
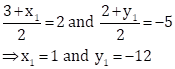
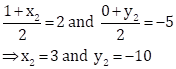
Hence, the coordinates of other two vertices of a parallelogram are (1, -12) and (3, -10).
Solution 39
ABCD is a parallelogram.
Then
Coordinates of midpoint of diagonal AC = Coordinates of midpoint of diagonal BD
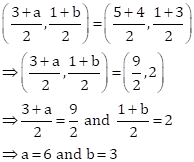
Solution 40
P and Q are the points of trisection and point P is nearer to A.
⇒ AP:PB = 1:2
Therefore, cordinates of P
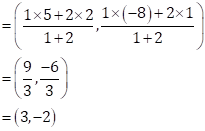
Now, point P lies on ![]() .
.
∴ 2(3) -
(-2) + ![]() = 0
= 0
⇒ ![]() = -8
= -8
Solution 41
Let the required ratio be ![]() .
.
Then, the
coordinates of point of division are ![]() .
.
But, it is a point on the y-axis and x-coordinate of every point on y-axis is zero.
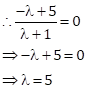
Hence, the required ratio is 5:1.
Putting ![]() in the coordinates
of point of division, we have
in the coordinates
of point of division, we have

Hence, the
coordinates of point of division are ![]() .
.
Solution 42
P![]() is the midpoint of points A(3, 4) and B(k, 6).
is the midpoint of points A(3, 4) and B(k, 6).
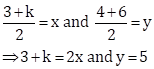
Now, ![]()
![]()

Solution 2
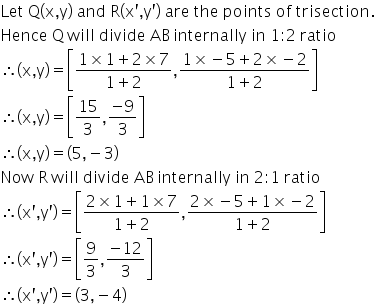
Co-ordinate Geometry Exercise Ex. 6C
Solution 1
(i)Let A(1, 2), B(-2, 3) and C(-3, -4) be the vertices ofthe given ΔABC, then
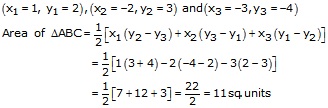
(ii)The coordinates of vertices of ΔABC are A(-5, 7), B(-4, -5) and C(4, 5)
Here, ![]()

(iii)The coordinates of ΔABC are A(3, 8), B(-4, 2) and C(5, -1)
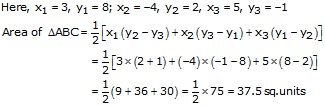
(iv)Let P(10, -6), Q(2, 5) and R(-1, 3) be the vertices of the given ΔPQR. Then,
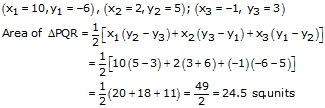
Solution 2
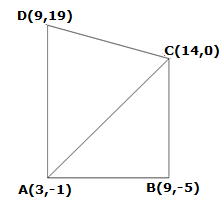

Solution 3
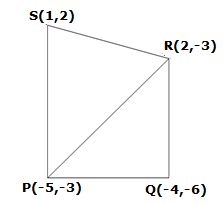

Solution 4
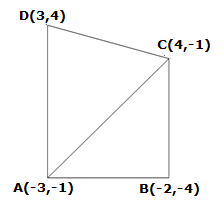
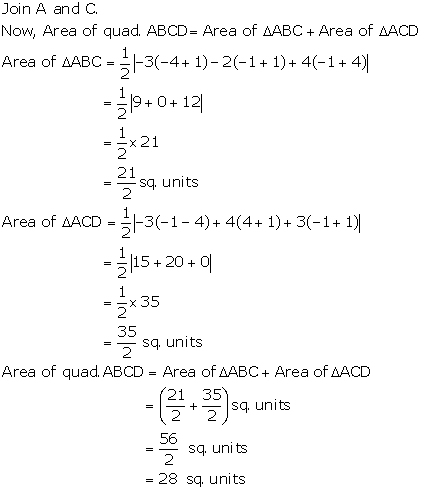
Solution 5
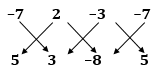
ABCD is a quadrilateral as follows:
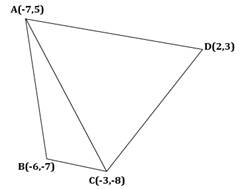
Area of quadrilateral ABCD = Area(ΔABC) + Area(ΔADC)
We have,
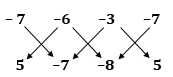
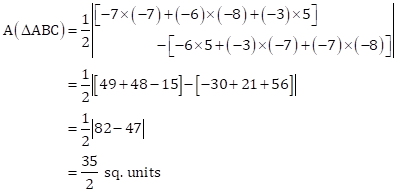
Also, we have
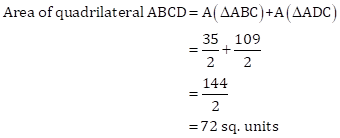
Solution 6
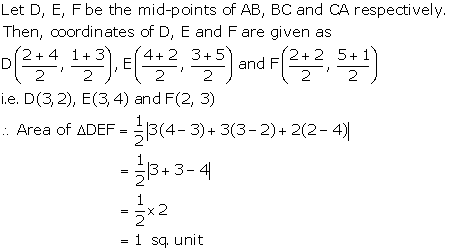
Solution 7
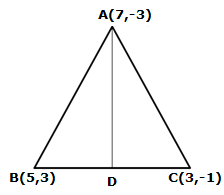

Solution 8
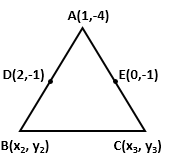
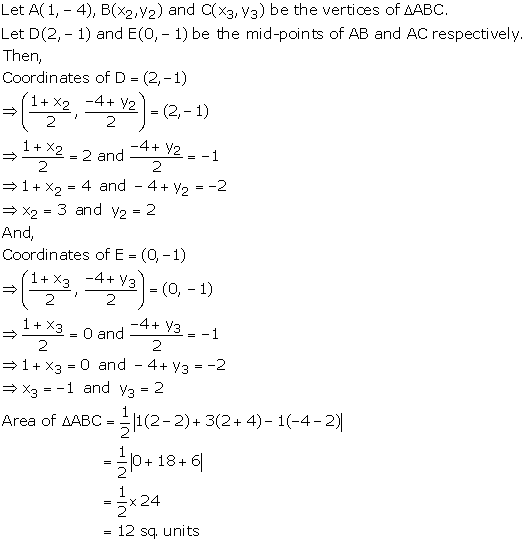
Solution 9


Solution 10
(i)
(ii)
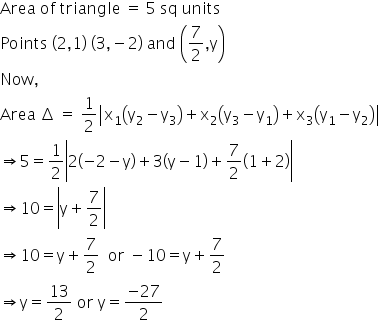
Solution 11
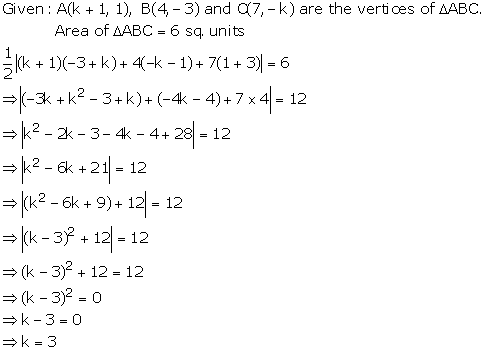
Solution 12
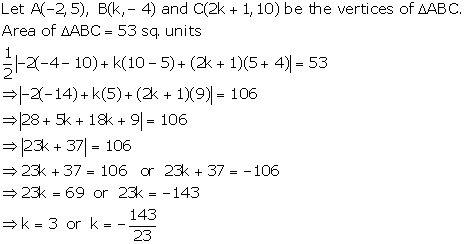
As k > 0
Hence,
k = 3
Solution 13(i)
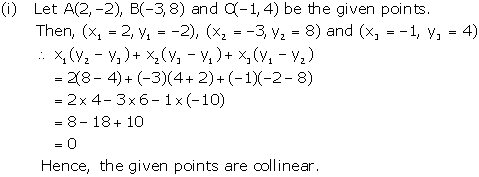
Solution 13(ii)
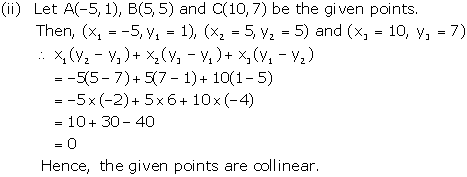
Solution 13(iii)
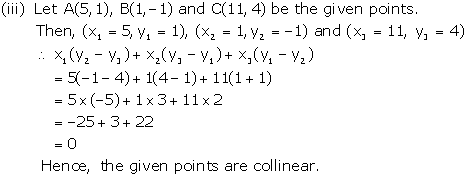
Solution 13(iv)

Solution 14
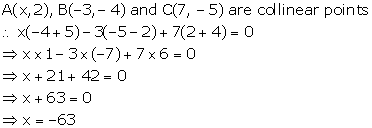
Solution 15
The given points are A(-3, 12), B(7, 6) and C(x, 9)
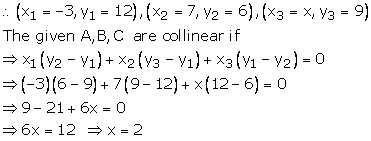
Solution 16
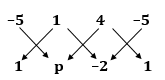
Given, points A(-5, 1), B(1, ![]() ) and C(4, -2) are
collinear.
) and C(4, -2) are
collinear.
∴ Area(ΔABC) = 0
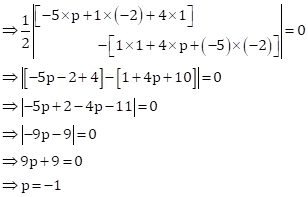
Solution 17
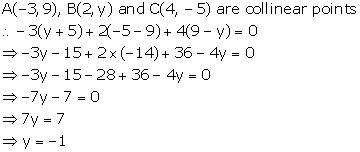
Solution 18
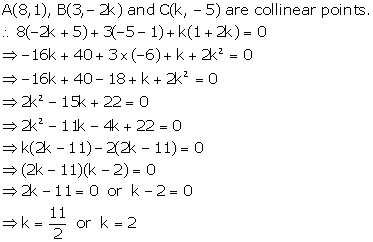
Solution 19
Given, points A(![]() ,
, ![]() ), B(1, 2) and C(7, 0) are collinear.
), B(1, 2) and C(7, 0) are collinear.
∴ Area(ΔABC) = 0
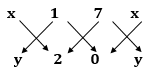
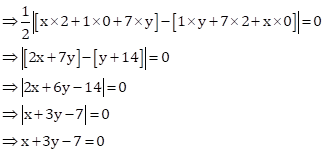
Solution 20
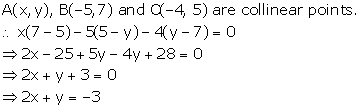
Solution 21
The vertices of ![]() ABC are (a, 0), (0, b), C(1, 1)
ABC are (a, 0), (0, b), C(1, 1)

The points A, B, C are collinear
![]() Area of
Area of ![]() ABC = 0
ABC = 0
![]() ab - a - b = 0
ab - a - b = 0 ![]() a + b = ab
a + b = ab
Dividing by ab

Solution 22
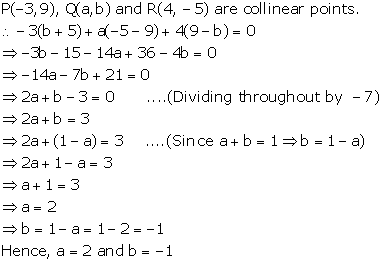
Solution 23
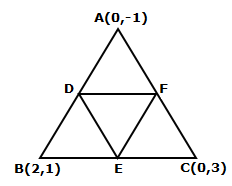

Solution 24
Let ![]() be the given points.
be the given points.
So, we have
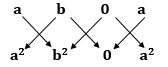
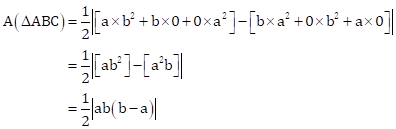
It is given that ![]() .
.
∴ Area(ΔABC) ≠ 0.
Hence, the given points will not be collinear.
Solution 25
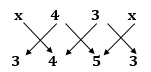
Let A(![]() , 3), B(4, 4) and C(3, 5) be the vertices of triangle.
, 3), B(4, 4) and C(3, 5) be the vertices of triangle.
Now, area(ΔABC) = 4
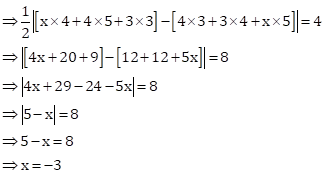
Co-ordinate Geometry Exercise Ex. 6D
Solution 1
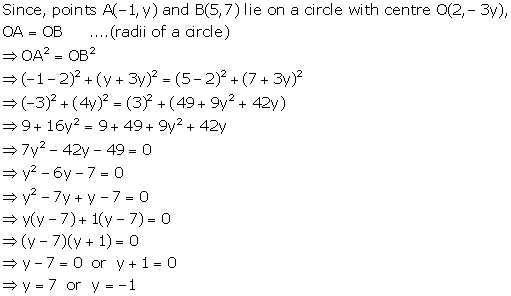
Solution 2
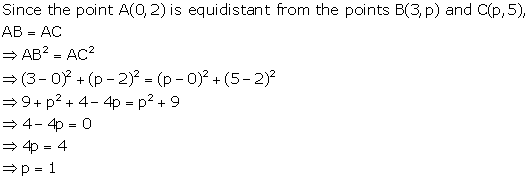
Solution 3
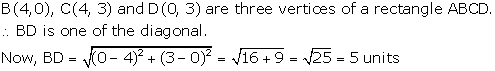
Solution 4

Solution 5

Solution 6
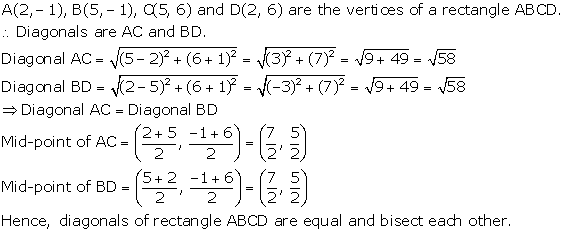
Solution 7
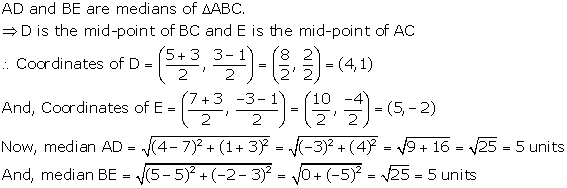
Solution 8
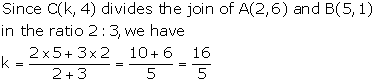
Solution 9
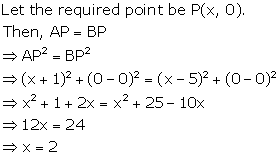
Solution 10
Distance between the points ![]()
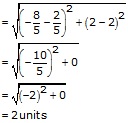
Solution 11
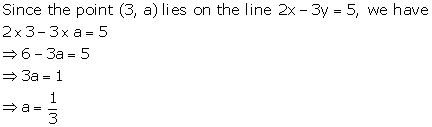
Solution 12
The points A(4,3) and B(x, 5) lie on the circle with center O(2,3)
OA and OB are radius of the circle.

Solution 13
The point P(x, y) is equidistant from the point A(7, 1) and B(3, 5)
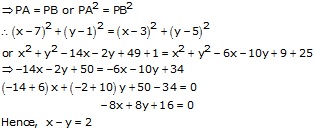
Solution 14
The vertices of ![]() ABC are (a, b), (b, c) and (c, a)
ABC are (a, b), (b, c) and (c, a)
Centroid is ![]()
But centroid is (0, 0)![]() a + b + c = 0
a + b + c = 0
Solution 15
The vertices of ![]() ABC are A(2, 2), B(-4, -4) and C(5, -8)
ABC are A(2, 2), B(-4, -4) and C(5, -8)
Centroid of ![]() ABC is given by
ABC is given by
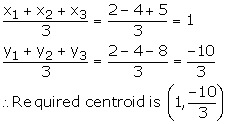
Solution 16
Let the point C(4, 5) divides the join of A(2, 3) and B(7, 8) in the ratio k : 1
The point C is ![]()
But C is (4, 5)
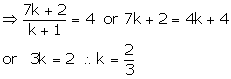
Thus, C divides AB in the ratio 2 : 3
Solution 17
The points A(2, 3), B(4, k) and C(6, -3) are collinear if area of ![]() ABC is zero
ABC is zero

But area of ![]() ABC = 0,
ABC = 0,
![]() k = 0
k = 0
Co-ordinate Geometry Exercise MCQ
Solution 1

Solution 2
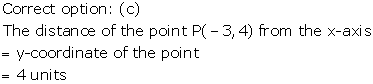
Solution 3

Solution 4
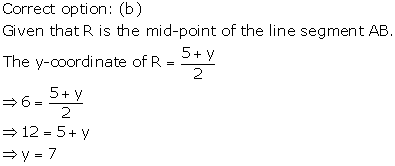
Solution 5

Solution 6
Correct option: (d)
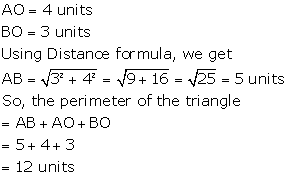
Solution 7
Correct option: (b)
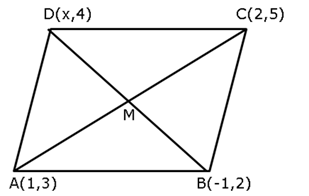

Solution 8
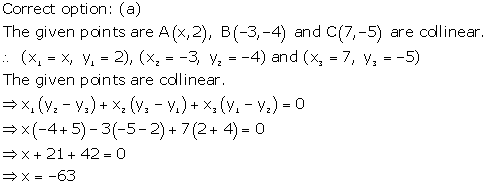
Solution 9

Solution 10
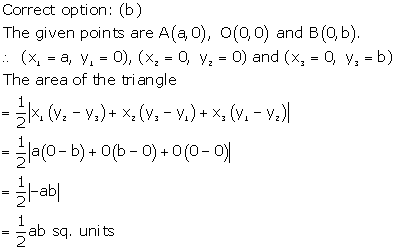
Solution 11

Solution 12
Correct option: (a)

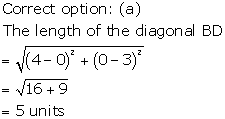
Solution 13

Solution 14

Solution 15

Solution 16

Solution 17

Solution 18

Solution 19

Solution 20

Solution 21

Solution 22

Solution 23

Solution 24

Solution 25

Solution 26
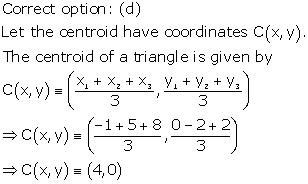
Solution 27

Solution 28

Solution 29

Solution 30
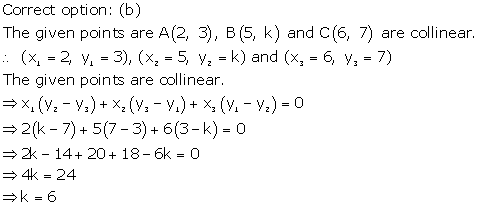
Solution 31
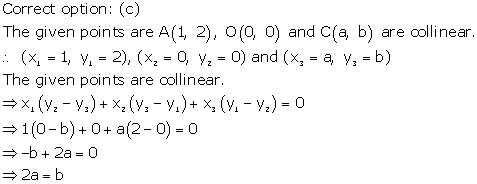
Solution 32

Solution 33

Solution 34