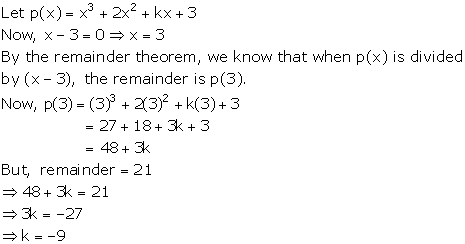Class 10 R S AGGARWAL AND V AGGARWAL Solutions Maths Chapter 2 - Polynomials
Polynomials Exercise Ex. 2A
Solution 1
Solution 2
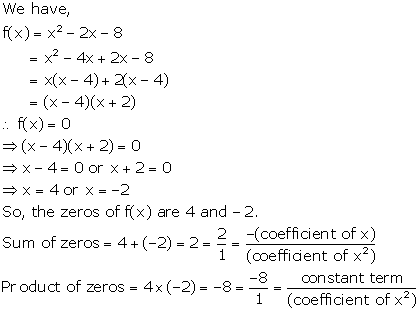
Solution 3
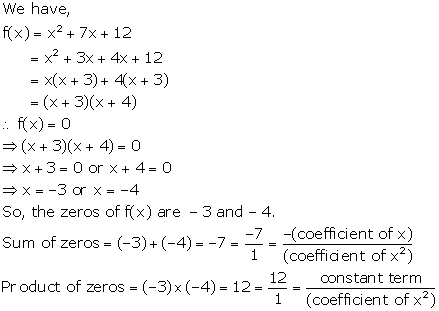
Solution 4
2x2 - x - 6 = 0
⇒ 2x2 - 4x + 3x - 6 = 0
⇒ 2x(x - 2) + 3(x - 2) = 0
⇒ (x - 2)(2x + 3) = 0
⇒ (x - 2) = 0 or (2x + 3) = 0
So, the zeroes of
the given quadratic polynomial are 2 and 
Sum of the zeros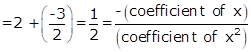 
Product of the
zeros 
Solution 5
We have
Solution 6
Solution 7
Solution 8
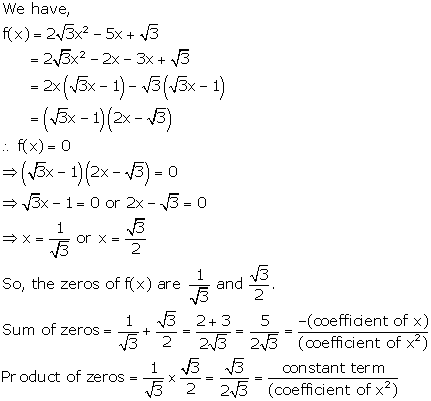
Solution 9
Solution 10
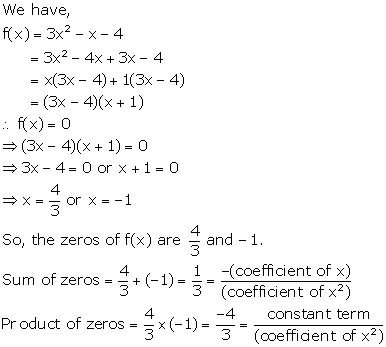
Solution 11
5x2 + 10x = 0
⇒ 5x(x + 2) = 0
⇒ 5x = 0 or (x + 2) = 0
⇒ x = 0 or x = -2
So, the zeroes of the given quadratic polynomial are 0 and -2.
Sum of the zeros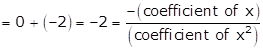 
Product of the
zeros 
Solution 12
Let
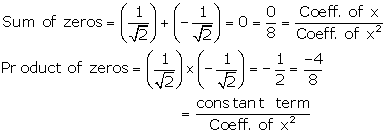
Solution 13
p(x) = 2x2 + 5x + k
Here, a = 2, b = 5 and c = k
α + β = 
and
αβ = 
α2 + β2
+ αβ = 
…. Given
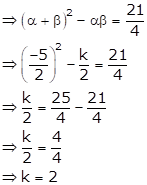
Solution 14
Solution 15
Solution 16
Solution 17
Let α = 2 and β = -6
Sum of zeros = α + β = 2 + (-6) = -4
Product of zeros = αβ = 2(-6) = -12
So, the required quadratic polynomial is
x2 - (α + β)x + αβ = x2 + 4x - 12
Here, a = 1, b = 4 and c = -12
Sum of the zeros 
Product of the zeros 
Solution 18
Solution 19
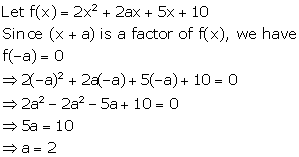
Solution 20
Since 
and 
are zeros of 
, we have
Solution 21
Let 
and 
be the zeros of
polynomial 
.
Then,
Now,
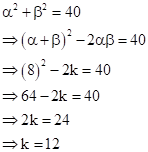
Polynomials Exercise Ex. 2B
Solution 1
Solution 2
Solution 3
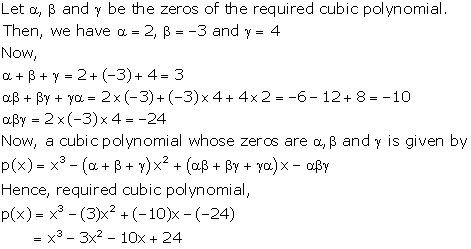
Solution 4
Solution 5
Solution 6
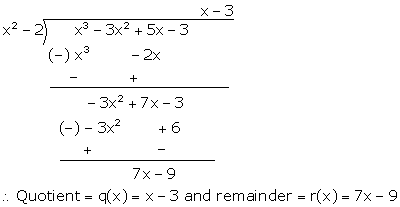
Solution 7
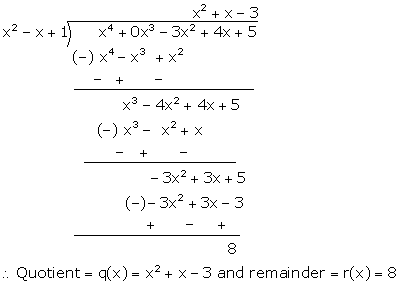
Solution 8
Solution 9
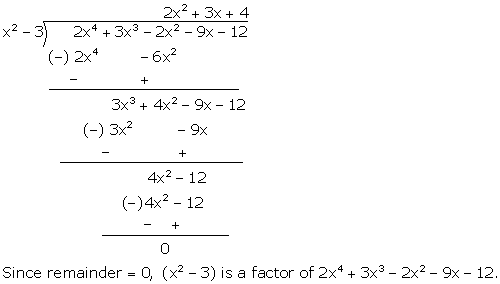
Solution 10
Here, remainder = 2x + 3 = px + q
⇒ p = 2 and q = 3
Solution 11
Solution 12
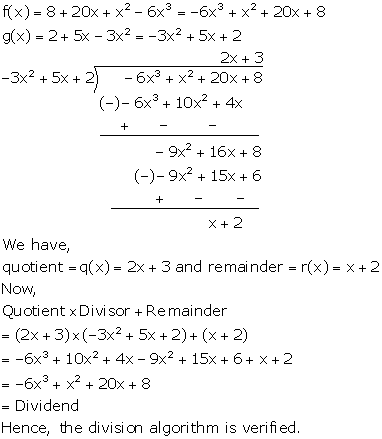
Solution 13
1
Solution 14
Solution 15
Solution 16
and 
are the zeros of the
polynomial 
.
Then,
will
divide the given polynomial completely.
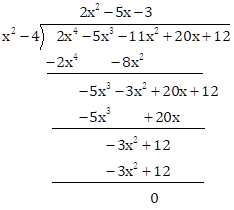
Now,
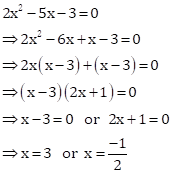
Therefore, the
zeros of the given polynomial are 
.
Solution 17
Solution 18
Solution 19
Here, f(x) = x4 + x3 - 14x2 - 2x + 24
Since, √2 and -√2 are two zeros of f(x)
⇒ (x - √2) and (x + √2) is a factor of f(x).
⇒ (x - √2) and (x + √2) = x - 2 is a factor of f(x).
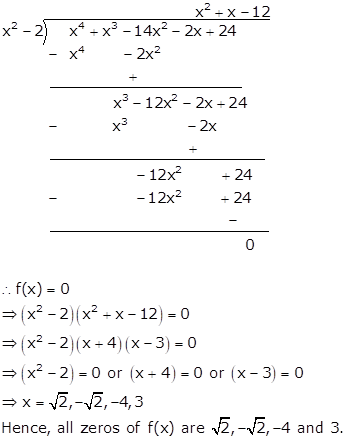
Solution 20
Here, f(x) = 2x4 - 13x3 + 19x2 + 7x - 3
Let α = (2 + √3) and β = (2 - √3). Then,
α + β = (2 + √3).+ (2 - √3) = 4
αβ = (2 + √3).(2 - √3) =4 - 3 = 1
So, the quadratic polynomial whose roots are α and β is given by
x2 - (α + β)x + αβ = x2 - 4x + 1
⇒ x2 - 4x + 1 is a factor of f(x).
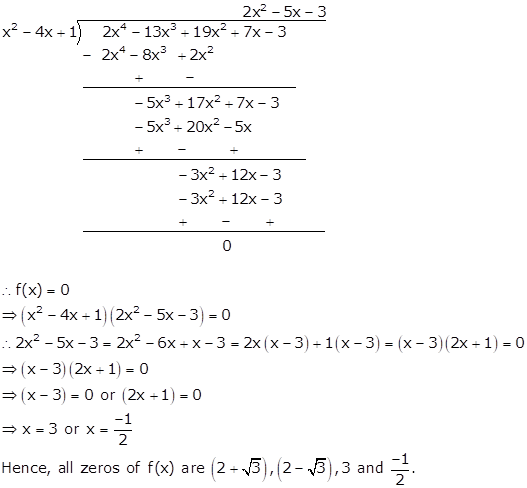
Solution 21
f(x) = 3x3 + 16x3 + 15x - 18
is one zero of f(x).
is a factor of f(x).
⇒ (3x - 2) is also a factor of f(x).
Now,
Hence, the zeros of the given polynomial are 
.
Solution 22
Here, f(x) = 2x4 - 3x3 - 3x2 + 6x - 2
1 and 
are
two zeros of f(x).
⇒ 
is a factor
of f(x).
⇒
is a factor
of f(x).
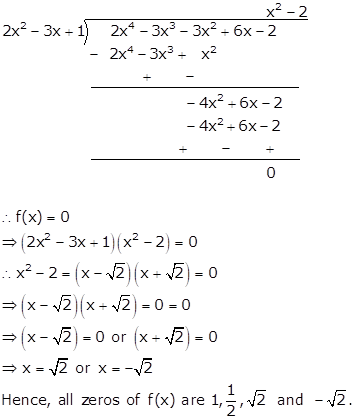
Solution 23
Polynomials Exercise Ex. 2C
Solution 1
Solution 2
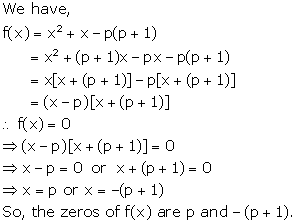
Solution 3
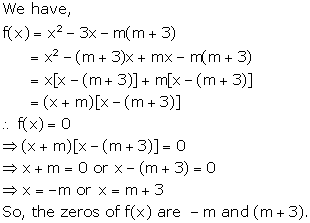
Solution 4
Solution 5
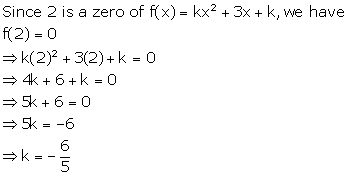
Solution 6
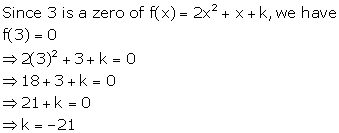
Solution 7
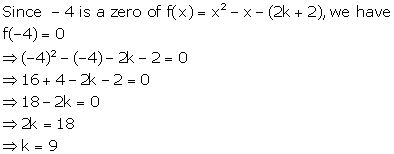
Solution 8
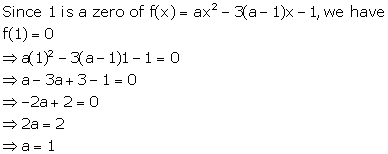
Solution 9
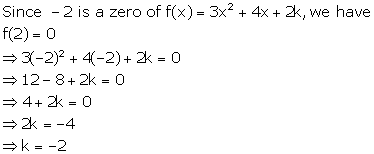
Solution 10
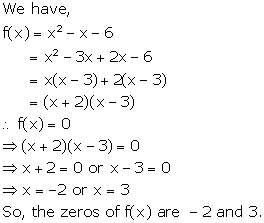
Solution 11
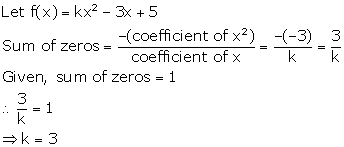
Solution 12
Solution 13
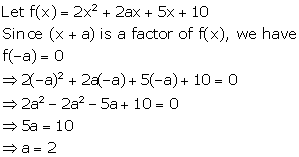
Solution 14
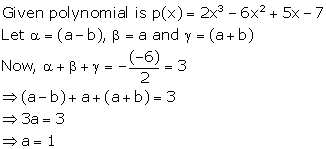
Solution 15
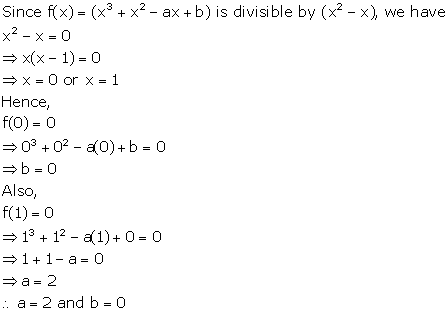
Solution 16
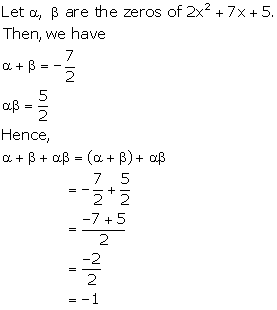
Solution 17
If f(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can always find polynomials q(x) and r(x) such that f(x) = q(x)g(x) + r(x),
where r(x) = 0 or degree r(x) < degree g(x).
Solution 18
Solution 19
Solution 20
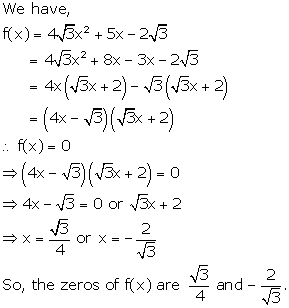
Solution 21
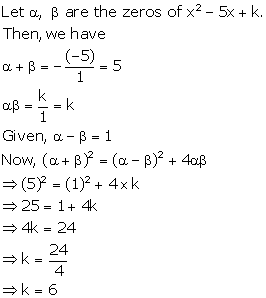
Solution 22
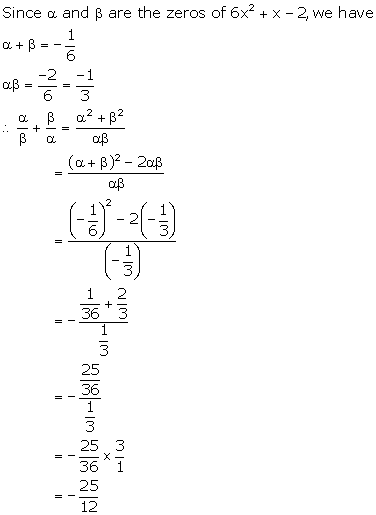
Solution 23
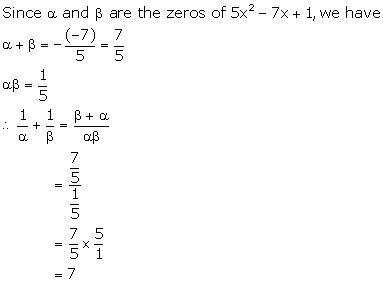
Solution 24
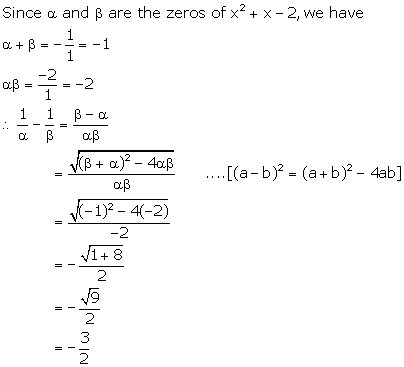
Solution 25
Polynomials Exercise MCQ
Solution 1
Correct answer: (d)
An expression of the form p(x) = a0 + a1x + a2x2 + ….. + anxn, where an ≠ 0, is called a polynomial in x of degree n.
Here, a0, a1, a2, ……, an are real numbers and each power of x is a non-negative integer.
Solution 2
Correct answer: (d)
An expression of the form p(x) = a0 + a1x + a2x2 + ….. + anxn, where an ≠ 0, is called a polynomial in x of degree n.
Here, a0, a1, a2, ……, an are real numbers and each power of x is a non-negative integer.
Solution 3
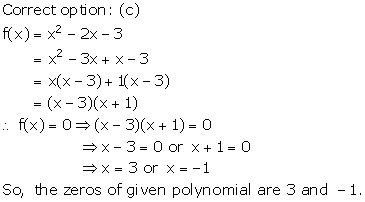
Solution 4
Solution 5
Solution 6
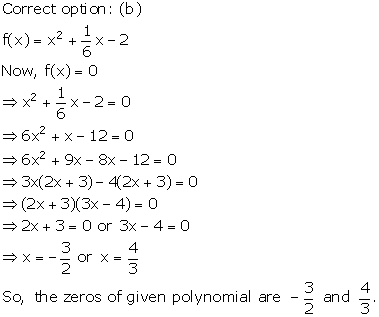
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
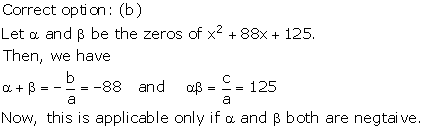
Solution 12
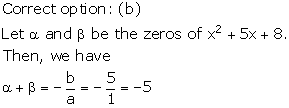
Solution 13
Correct option: (c)
be the zeros of 
.
Then,
Solution 14
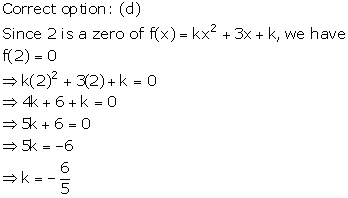
Solution 15
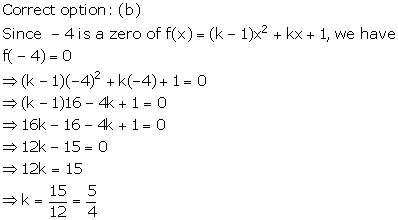
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
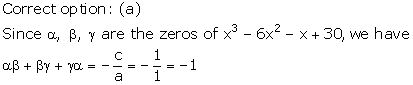
Solution 21
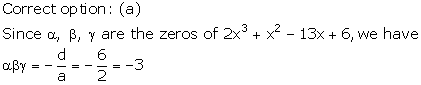
Solution 22
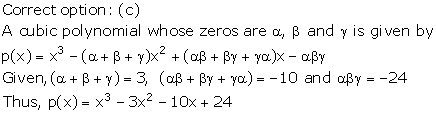
Solution 23
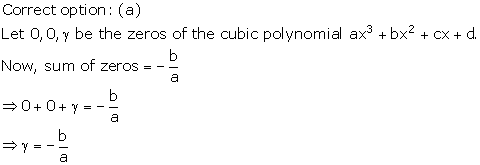
Solution 24
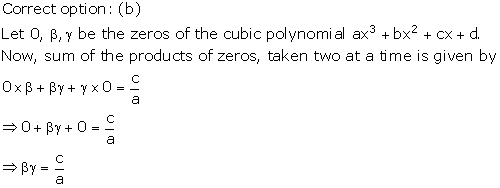
Solution 25
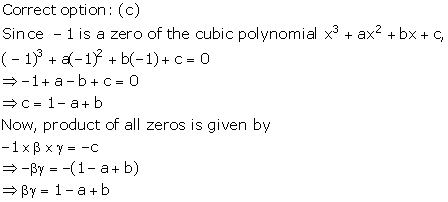
Solution 26
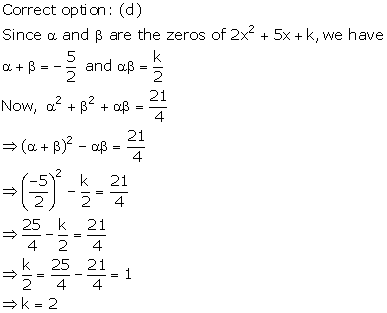
Solution 27
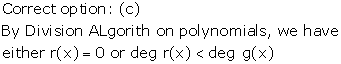
Solution 28
Polynomials Exercise Test Yourself
Solution 1
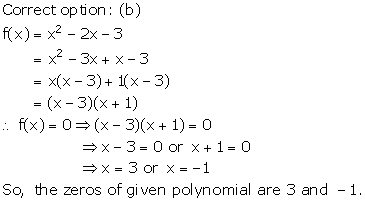
Solution 2
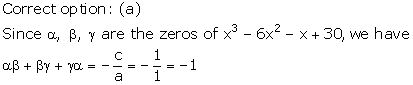
Solution 3
Solution 4
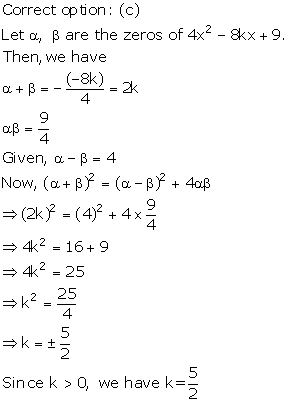
Solution 5
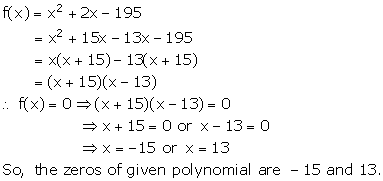
Solution 6
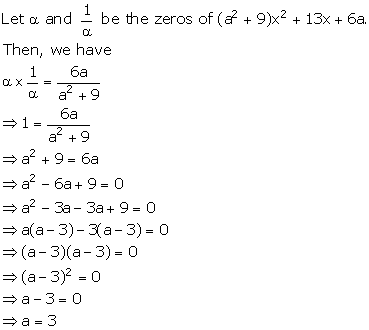
Solution 7
Solution 8
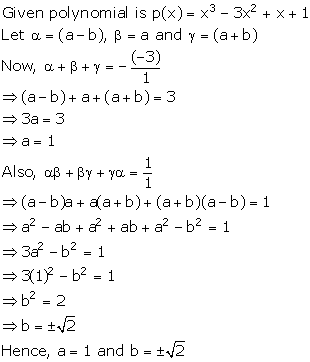
Solution 9
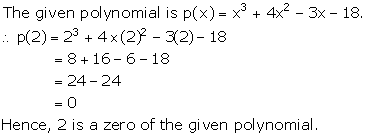
Solution 10
Solution 11
Solution 12
Solution 13
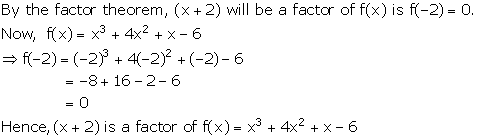
Solution 14
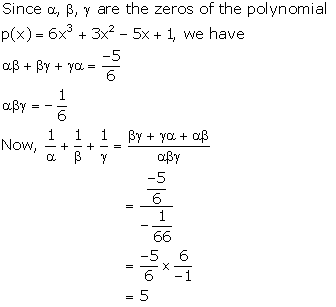
Solution 15
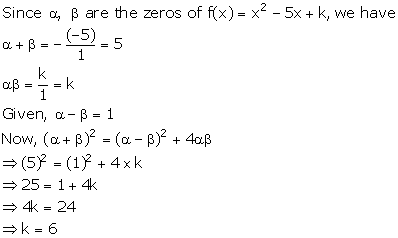
Solution 16
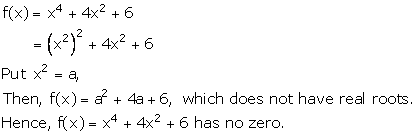
Solution 17
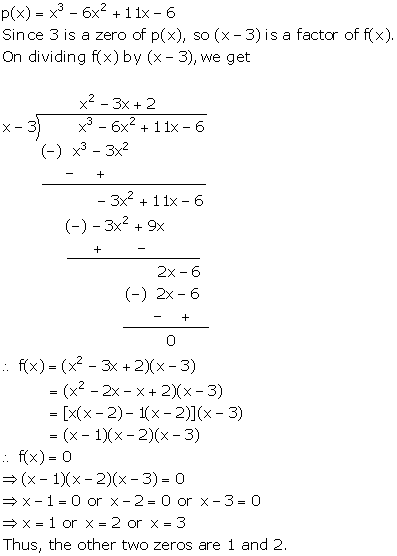
Solution 18
Solution 19
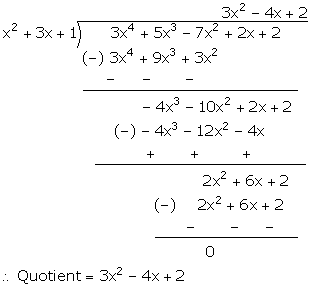
Solution 20
