Class 9 NCERT Solutions Maths Chapter 3 - Coordinate Geometry
Ex. 3.1
Ex. 3.2
Coordinate Geometry Exercise Ex. 3.1
Solution 1
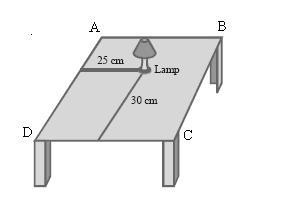
Consider that the lamp is placed on the table. Here two references must be used to ascertain the position. Choose two adjacent edges DC and AD. Now draw perpendiculars on the two edges from the position of lamp and measure the lengths of these perpendiculars. Let the length of these perpendiculars be 30 cm and 25 cm respectively. Now the position of the lamp from the left edge (AD) is 25 cm and from the lower edge (DC) is 30 cm. Then the position of the table will be given by the points (25, 30).
Concept Insight: Since there are two dimensions length and breadth of the table so two references are required to ascertain the position on the table. The point where the two edges of table can be taken as the references In this case we can have origin at any of the four corners. The perpendicular distance from the edges will give the position of lamp. Remember that (25, 30) and (30, 25) represent two different positions on the table.
Solution 2
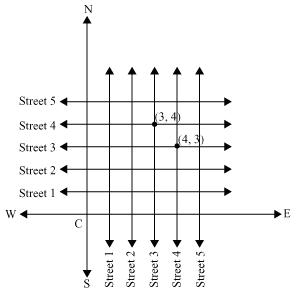
Both the cross- streets are marked in the above figure. We may observe that there is only one cross street which can be referred as (4, 3) and also only one which can be referred as (3, 4).
Concept Insight: Consider north-south and west-east directions as two perpendicular axes. The point where the two axes intersect is called the origin. Drawing line parallel to x axis and y axis will give the five streets for each of the two given directions. Any point (x,y) on Cartesian plane represents a distance of x units from y axis and y units from x axis. Coordinate points (x,y) and (y,x) represents two different positions on a plane if 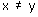 . Each coordinate point on the Cartesian plane determines a unique position.
. Each coordinate point on the Cartesian plane determines a unique position.
Coordinate Geometry Exercise Ex. 3.2
Solution 1
(i) The name of horizontal lines and vertical lines drawn to determine the position of any point in the Cartesian plane is x-axis and y axis respectively.
(ii) The name of each part of the plane formed by these two lines x-axis and y-axis is called as quadrants (one fourth part)
(iii) Name of the point where there two lines intersect is called as origin.
(ii) The name of each part of the plane formed by these two lines x-axis and y-axis is called as quadrants (one fourth part)
(iii) Name of the point where there two lines intersect is called as origin.
Concept Insight: The question is based on factual knowledge remember that the horizontal and vertical lines drawn to determine the position are called x-axis and y axis respectively. The point where these two axes intersect is called the origin and these axes divide the coordinate plane into four parts called the 4 quadrants.
Solution 2
(i) The x coordinate and y coordinate of point B are - 5 and 2 respectively. So the coordinates of point B is (- 5, 2)..
(ii) The x coordinate and y coordinate of point C are 5 and - 5 respectively. So the coordinates of point C is (5, - 5).
(iii) The point whose x coordinate and y coordinate are - 3 and - 5 respectively is point E.
(iv) The point whose x coordinate and the y coordinate are 2 and - 4 respectively is point G.
(v) The x coordinate of point D is 6. So, abscissa of the point D is 6.
(vi) The y coordinate of point H is - 3. So, ordinate of point H is - 3.
(vii) The x coordinate and y coordinate of point L are 0 and 5 respectively. So coordinates of point L is (0, 5).
(viii) The x coordinate and y coordinate of point M are - 3 and 0 respectively. So the coordinates of point M is (- 3, 0).
Concept Insight: For an ordered pair(x, y) in the coordinate plane, x is the distance of the point from Y axis also called the abscissa and y is the distance of the point from X axis also called the ordinate.
Remember that while locating the position of a point we always write x coordinate first and then y coordinate, the two coordinate points are always written in a closed bracket and are separated by a comma.

