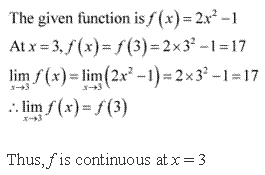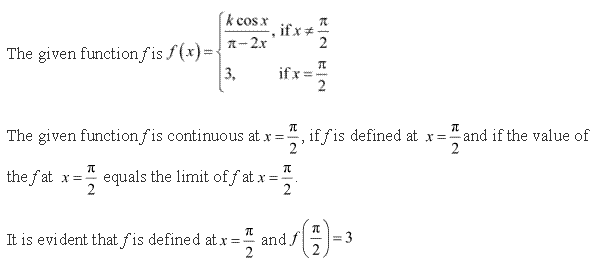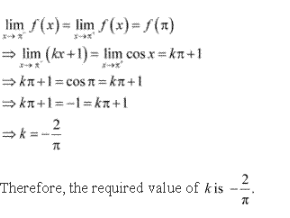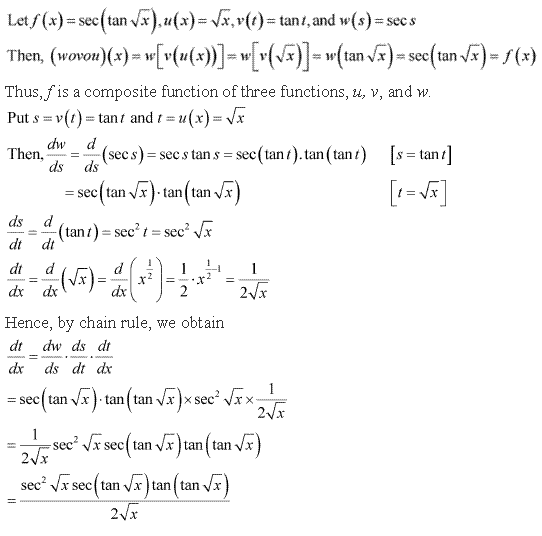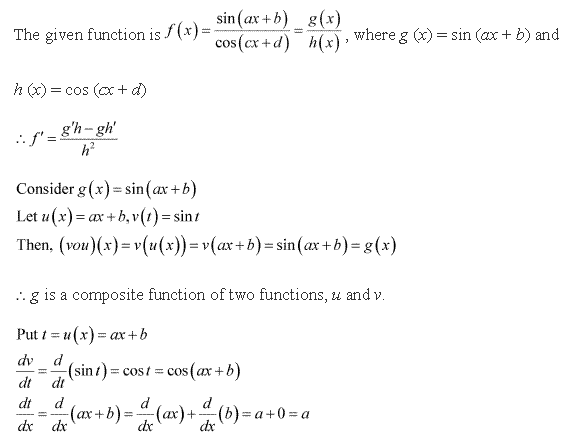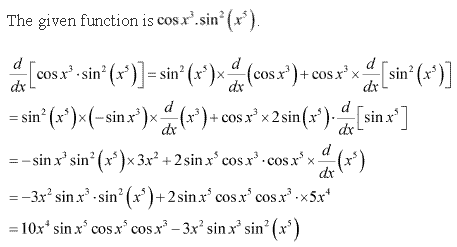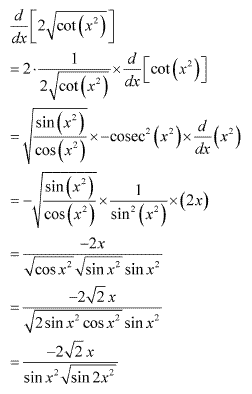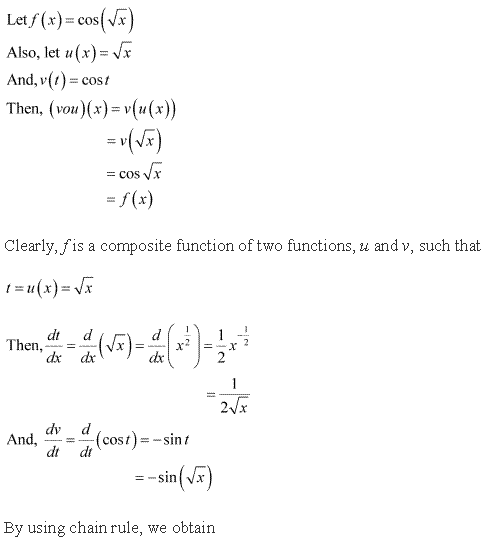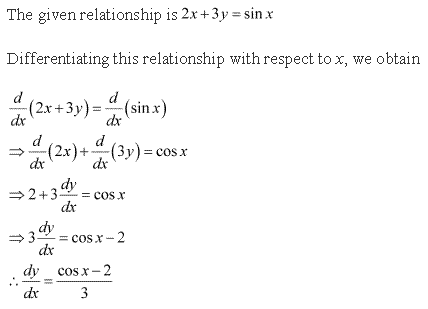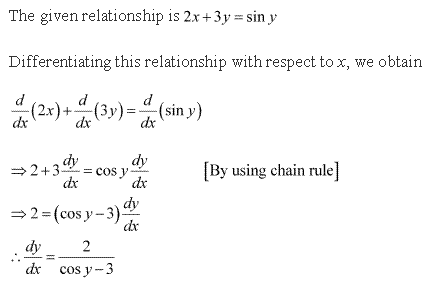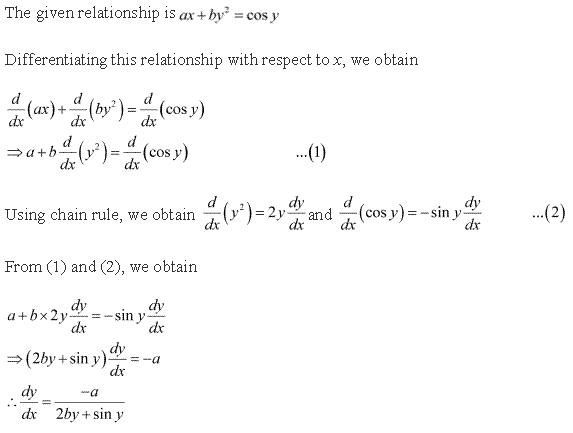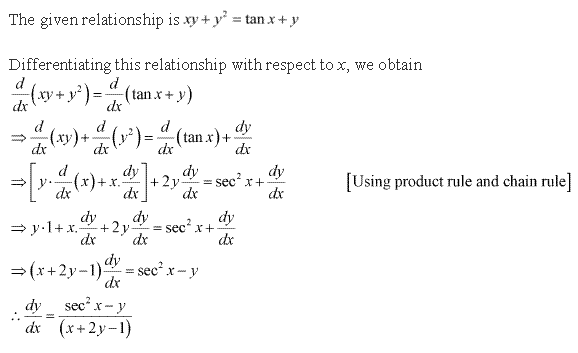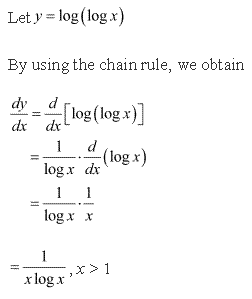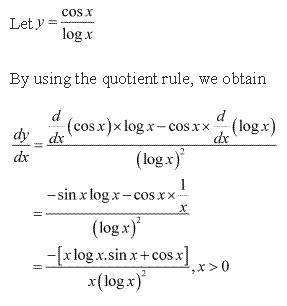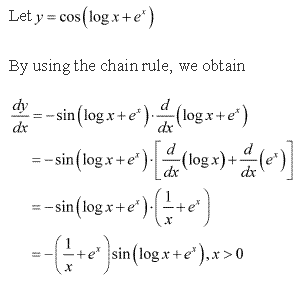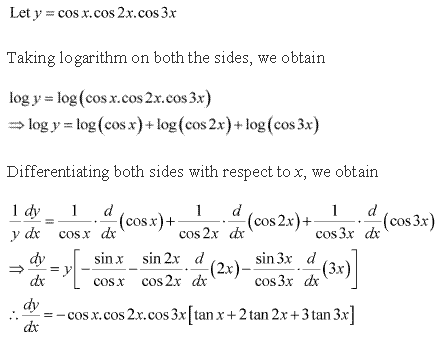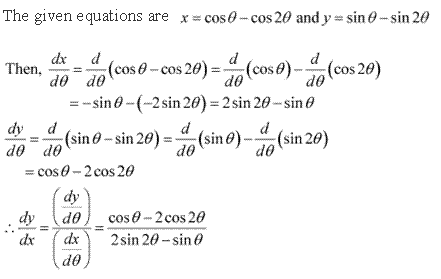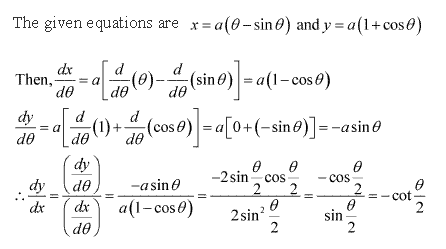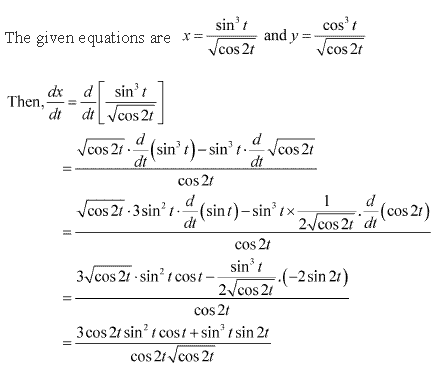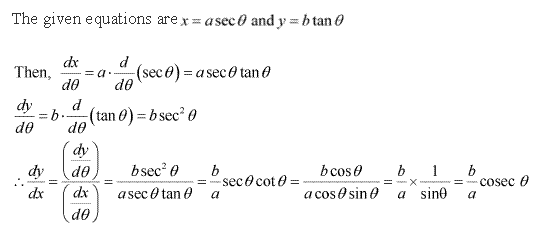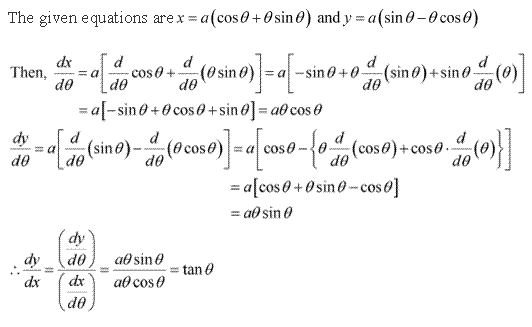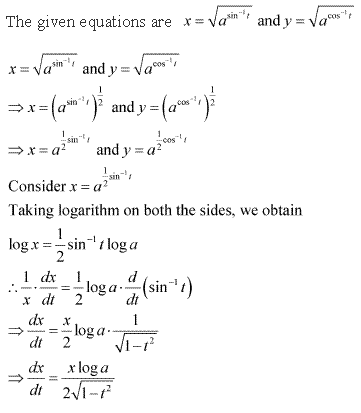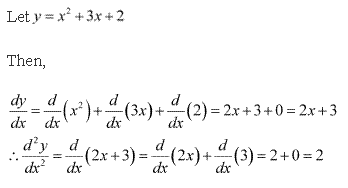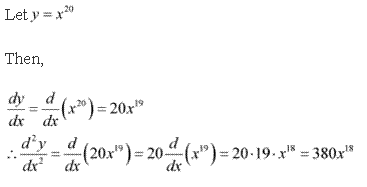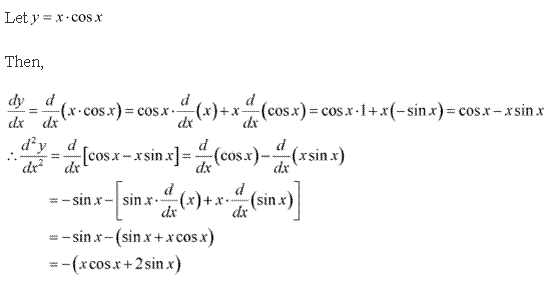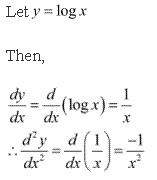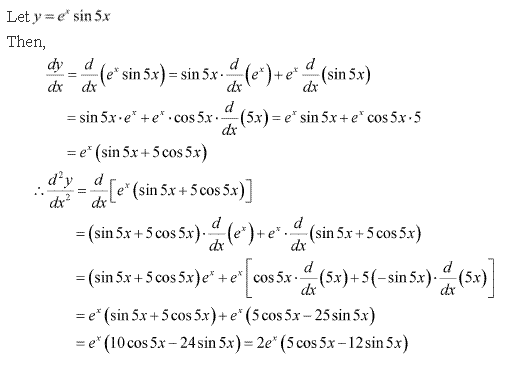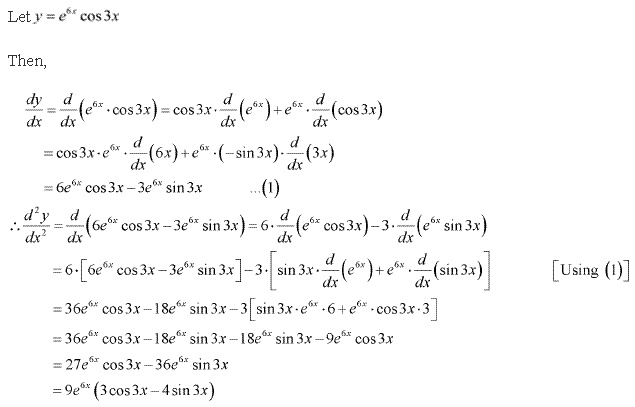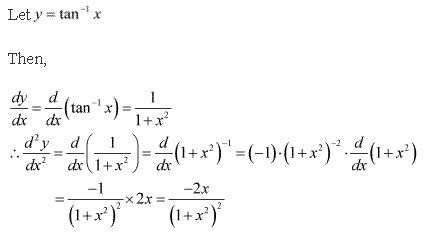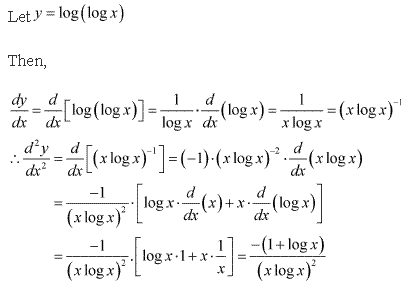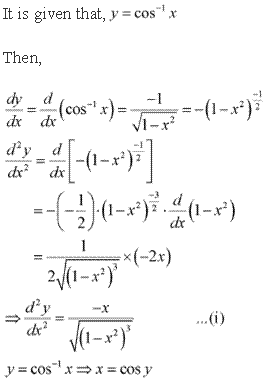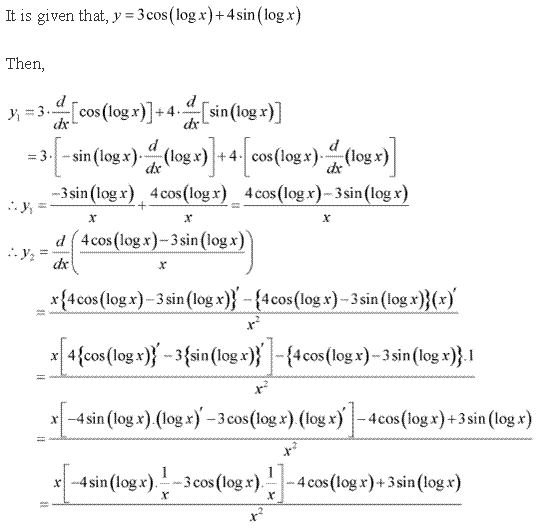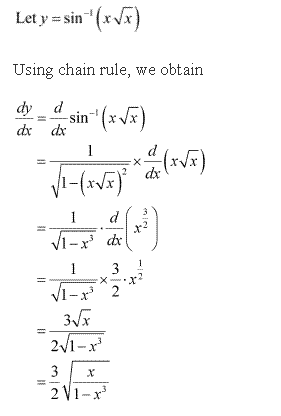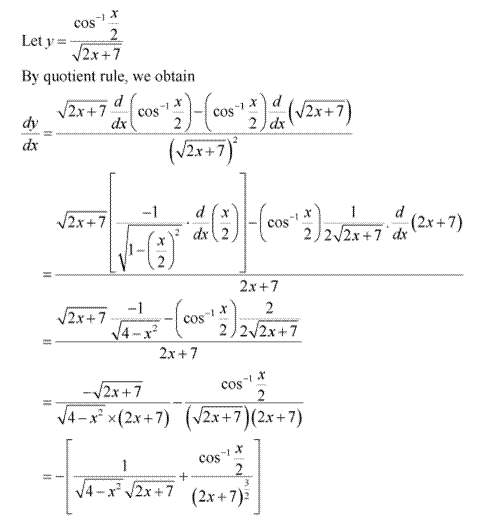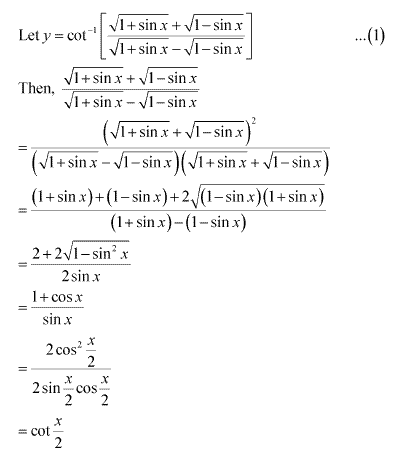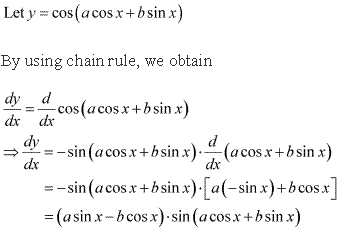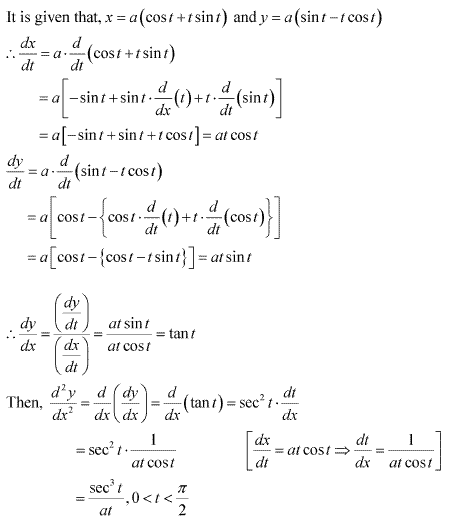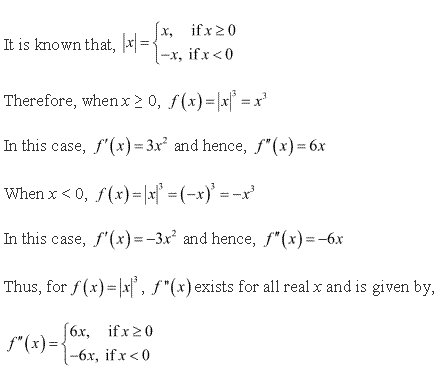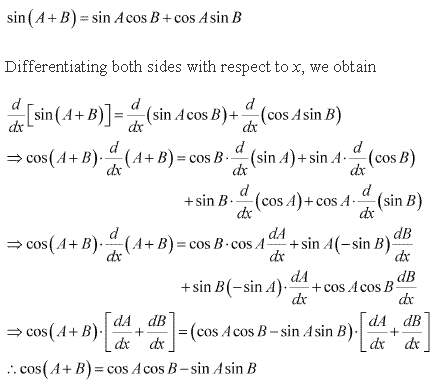NCERT Solutions for Class 12-science Maths Chapter 5 - Continuity and Differentiability
Chapter 5 - Continuity and Differentiability Exercise Ex. 5.1
Solution 1
The given function is f(x) = 5x - 3
At x = 0, f(0) = 5 × 0 - 3 = -3
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Thus, from the above observation, it can be concluded that x = 1 is the only point of discontinuity.
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
The given function is f(x) = x2 - sinx + 5
It is evident that f is defined at x = ∏
Solution 21
Solution 22
Therefore, cosecant is continuous except at x = np, n 
Z
Z
Therefore, cotangent is continuous except at x = np, n 
Z
ZSolution 23
Solution 24
Solution 25
Solution 26
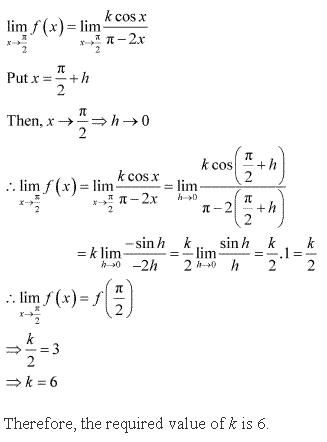
Solution 27
Solution 28
The given function f is continuous at x = 
, if f is defined at x = and if the value
of f at x = equals the limit of f at x =
Solution 29
Solution 30
Solution 31
Solution 32
Solution 33
Solution 34
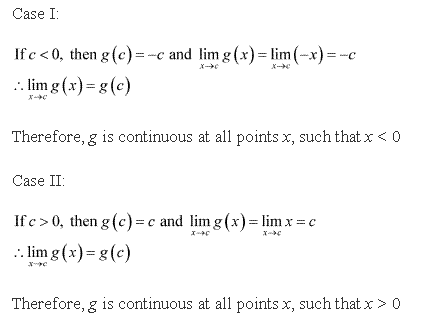
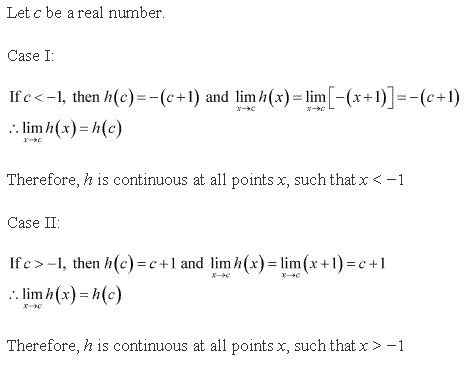
Chapter 5 - Continuity and Differentiability Exercise Ex. 5.2
Solution 1
Then, (v ο u)(x) = v(u(x)) = v(x2 + 5) = sin (x2 + 5) = f(x)
Solution 2
Solution 3
Solution 4
Solution 5
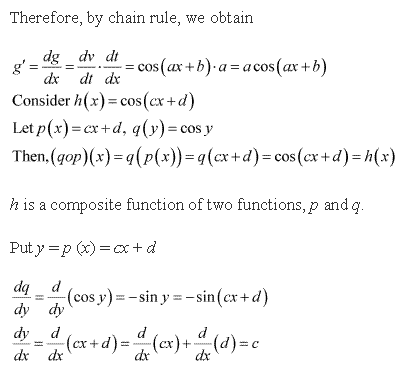
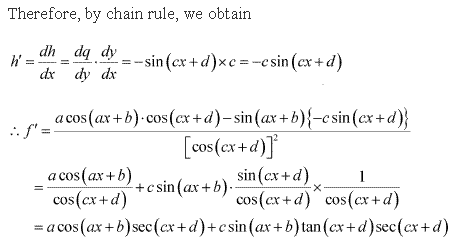
Solution 6
Solution 7
Solution 8
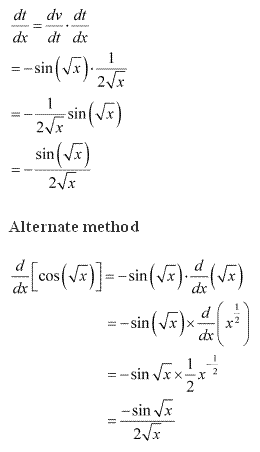
Solution 9
Solution 10
Chapter 5 - Continuity and Differentiability Exercise Ex. 5.3
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
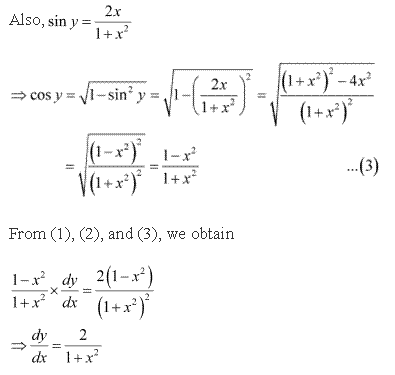
Solution 10
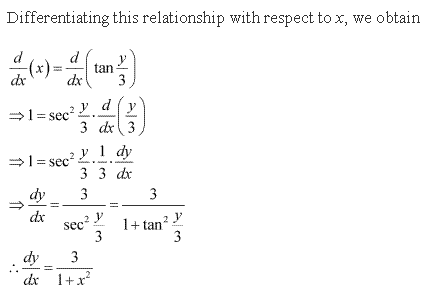
Solution 11
Solution 12
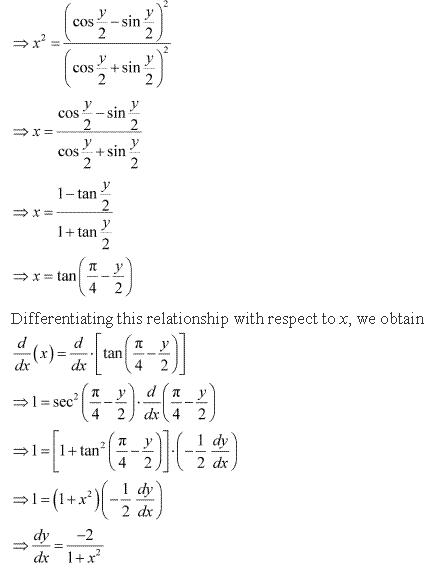
Solution 13
Solution 14
Solution 15
Chapter 5 - Continuity and Differentiability Exercise Ex. 5.4
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Chapter 5 - Continuity and Differentiability Exercise Ex. 5.5
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
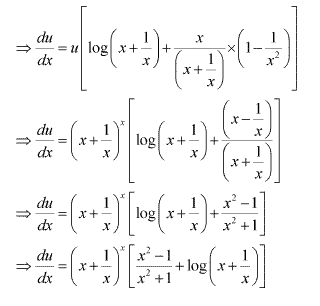
Solution 7
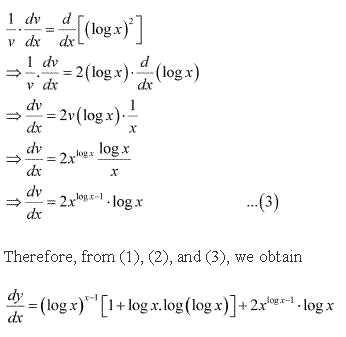
Solution 8
Solution 9
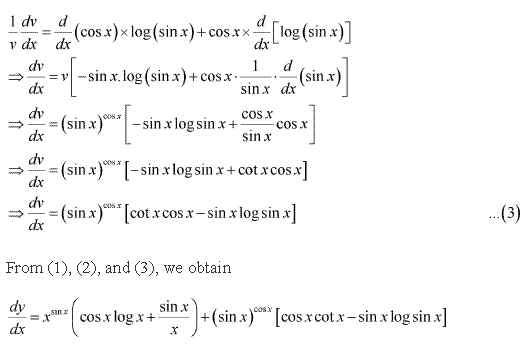
Solution 10
Solution 11
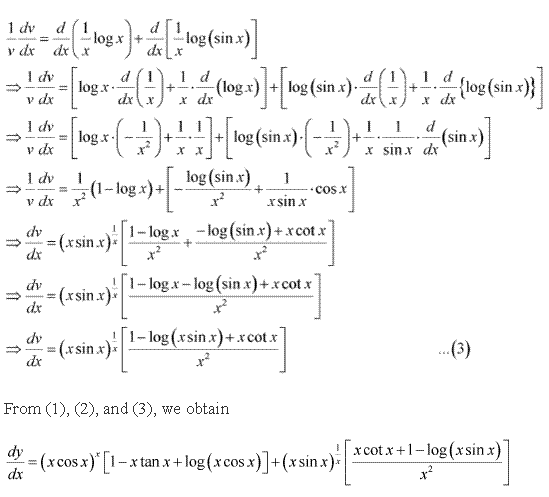
Solution 12
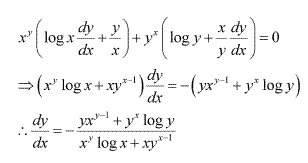
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
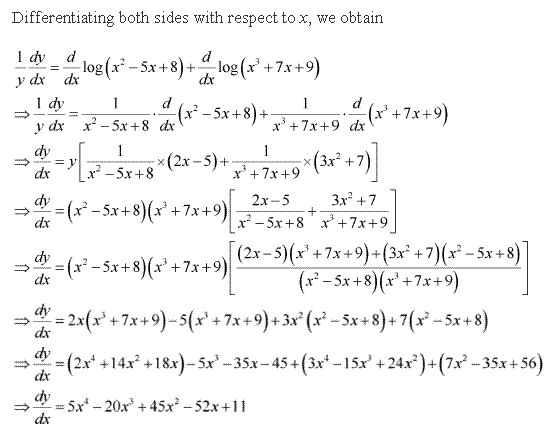
Solution 18
Chapter 5 - Continuity and Differentiability Exercise Ex. 5.6
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
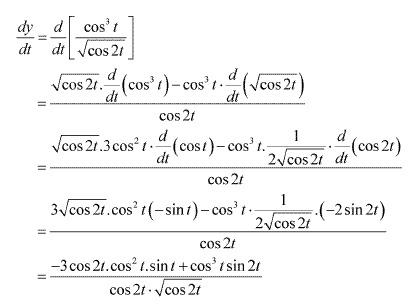
Solution 8
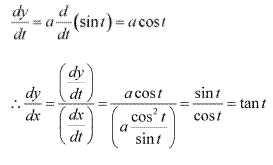
Solution 9
Solution 10
Solution 11
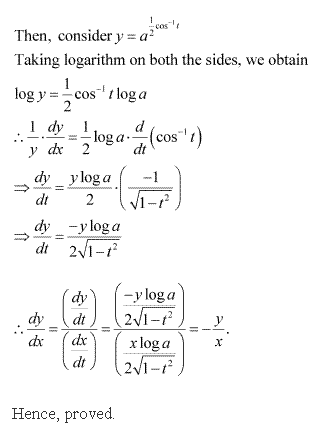
Chapter 5 - Continuity and Differentiability Exercise Ex. 5.7
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
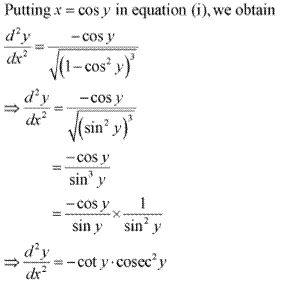
Solution 13
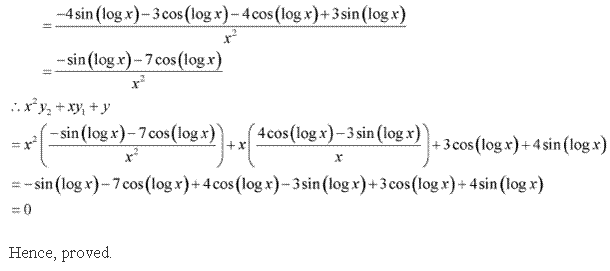
Solution 14
Solution 15
Solution 16
Solution 17
Chapter 5 - Continuity and Differentiability Exercise Ex. 5.8
Solution 1
Rolle's theorem states that there is a point c 
(-4, -2) such that f'(c) = 0
Solution 2
then there exists some c (a, b) such that f'(c) = 0
Let n be an integer such that n (5, 9).
Let n be an integer such that n (-2, 2).
Solution 3
Therefore, by the Mean Value Theorem, there exists c (-5, 5) such that
Solution 4
Mean Value Theorem states that there is a point c (1, 4) such that f'(c) = 1
Solution 5
Solution 6
Chapter 5 - Continuity and Differentiability Exercise Misc. Ex.
Solution 1
Solution 2
Solution 3
Solution 4
Solution 5
Solution 6
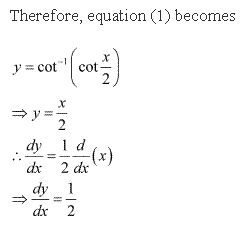
Solution 7
Solution 8
Solution 9
where sin x > cosx
Solution 10
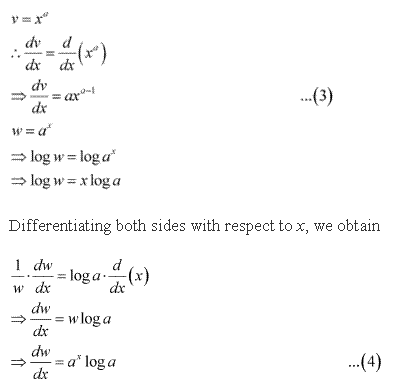
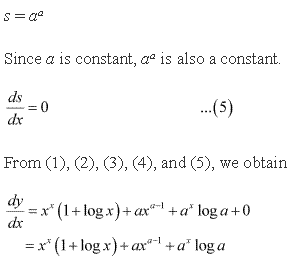
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Hence, proved.
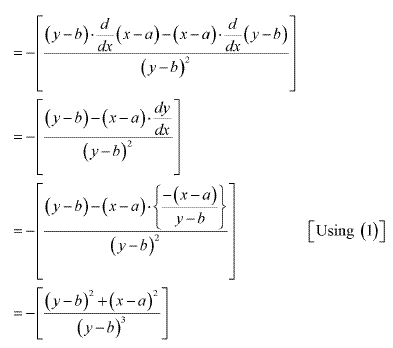
Solution 16
Solution 17
Solution 18
Solution 19
Solution 20
Solution 21
Yes.
Consider the function f(x)=|x-1|+|x-2|
Since we know that the modulus function is continuous everywhere, so there sum is also continuous
Therefore, function f is continuous everywhere
Now, let us check the differentiability of f(x) at x=1,2
At x=1
LHD = 
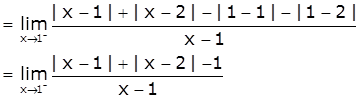
[Take x=1-h, h>0 such that h→0 as x→1-]
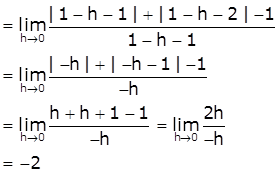
Now,
RHD = 
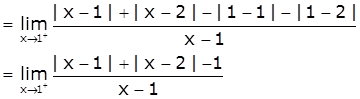
[Take x=1+h, h>0 such that h→0 as x→1+]
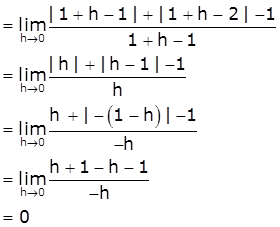
≠ LHD
Therefore, f is not differentiable at x=1.
At x=2
LHD = 
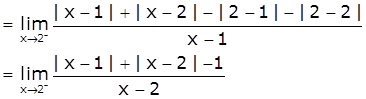
[Take x=2-h, h>0 such that h→0 as x→2-]
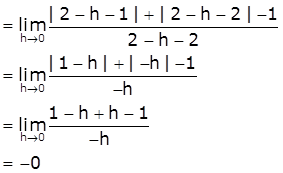
Now,
RHD = 
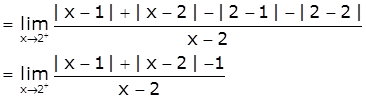
[Take x=2+h, h>0 such that h→0 as x→2+]
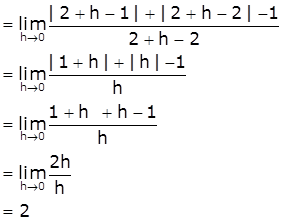
≠ LHD
Therefore, f is not differentiable at x=2.
Hence, f is not differentiable at exactly two points.
Solution 22
Solution 23
Kindly Sign up for a personalised experience
- Ask Study Doubts
- Sample Papers
- Past Year Papers
- Textbook Solutions
Sign Up
Verify mobile number
Enter the OTP sent to your number
Change