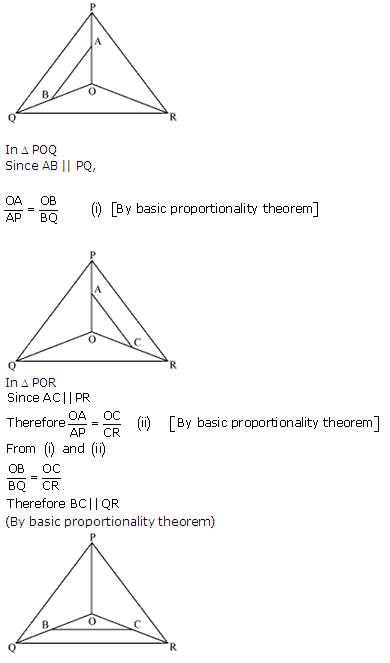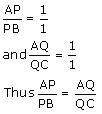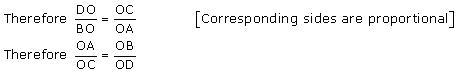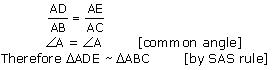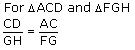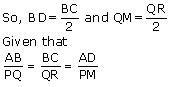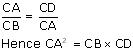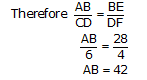Class 10 NCERT Solutions Maths Chapter 6 - Triangles
Triangles Exercise Ex. 6.1
Solution 1
(i) All circles are SIMILAR.
(ii) All squares are SIMILAR.
(iii) All EQUILATERAL triangles are similar.
(iv) Two polygons of same number of sides are similar, if their corresponding angles are EQUAL and their corresponding sides are PROPORTIONAL.
Solution 2
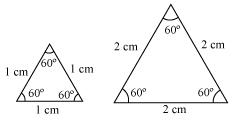
(i) Two equilateral triangles with sides 1 cm and 2 cm.
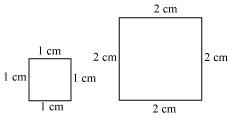
Two squares with sides 1 cm and 2 cm
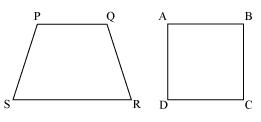
(ii) Trapezium and Square
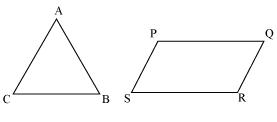
Triangle and Parallelogram
Solution 3
Quadrilateral PQRS and ABCD are not similar as their corresponding sides are proportional i.e. 1:2 but their corresponding angles are not equal.
Triangles Exercise Ex. 6.2
Solution 1
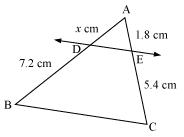
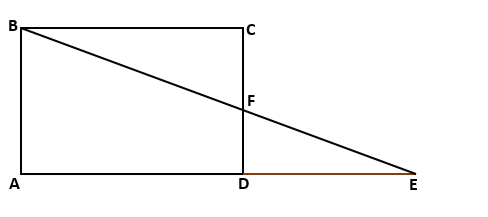
(i)
Let EC = x
Since DE || BC.
Therefore, by basic proportionality theorem,
(ii)
Let AD = x
Since DE || BC,
Therefore by basic proportionality theorem,
Solution 2
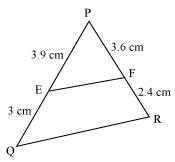
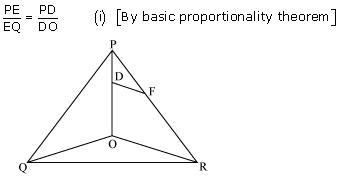
(i)
Given that PE = 3.9, EQ = 3, PF = 3.6, FR = 2.4
Now,
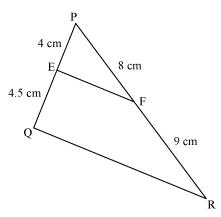
(ii)
PE = 4, QE = 4.5, PF = 8, RF = 9
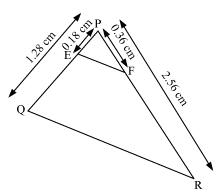
(iii)
PQ = 1.28, PR = 2.56, PE = 0.18, PF = 0.36
Solution 3
In the given figure
Since LM || CB,
Therefore by basic proportionality theorem,
Solution 4
In Δ ABC,
Since DE || AC
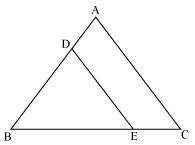
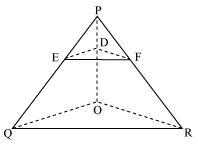
Solution 5
In Δ POQ
Since DE || OQ
Solution 6
Solution 7
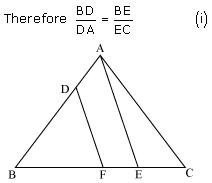
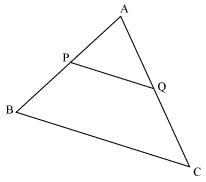
Consider the given figure
PQ is a line segment drawn through midpoint P of line AB such that PQ||BC
i.e. AP = PB
Now, by basic proportionality theorem
i.e. AQ = QC
Or, Q is midpoint of AC.
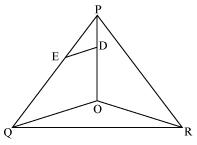
Solution 8
Consider the given figure
PQ is a line segment joining midpoints P and Q of line AB and AC respectively.
i.e. AP = PB and AQ = QC
Now, we may observe that
And hence basic proportionality theorem is verified
So, PQ||BC
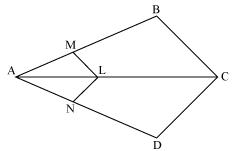
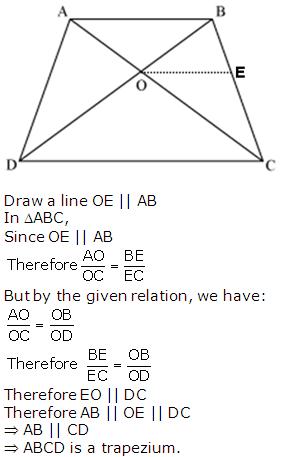
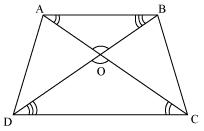
Solution 9
Solution 10
Triangles Exercise Ex. 6.3
Solution 1
(i) ∠A = ∠P = 60°
∠B = ∠Q = 80
∠C = ∠R = 40°
Therefore Δ ABC ~ Δ PQR [by AAA rule]
(iii) Triangles are not similar as the corresponding sides are not proportional.
(iv) Triangles are not similar as the corresponding sides are not proportional.
(v) Triangles are not similar as the corresponding sides are not proportional.
(vi) In Δ DEF
∠D + ∠E + ∠F = 180°
(Sum of measures of angles of a triangle is 180)
70° + 80° + ∠F = 180°
∠F = 30°
Similarly in ∠PQR
∠P + ∠Q + ∠R = 180°
(Sum of measures of angles of a triangle is 180)
∠P + 80° +30° = 180°
∠P = 70°
Now In Δ DEF and Δ PQR
∠D = ∠P = 70°
∠E = ∠Q = 80°
∠F = ∠R = 30°
Therefore Δ DEF ~ Δ PQR [by AAA rule]
Solution 2
Since DOB is a straight line
Therefore ∠DOC + ∠COB = 180°
Therefore ∠DOC = 180° - 125°
= 55°
In ∠DOC,
∠DCO + ∠CDO + ∠DOC = 180°
∠DCO + 70° + 55° = 180°
∠DCO = 55°
Since Δ ODC ~ Δ OBA,
Therefore ∠OCD = ∠OAB [corresponding angles equal in similar triangles]
Therefore ∠OAB = 55°
Solution 3
In Δ DOC and Δ BOA
AB || CD
Therefore ∠CDO = ∠ABO [Alternate interior angles]
∠DCO = ∠BAO [Alternate interior angles]
∠DOC = ∠BOA [Vertically opposite angles]
Therefore Δ DOC ~ Δ BOA [AAA rule)
Solution 4
In Δ PQR
∠PQR = ∠PRQ
Therefore PQ = PR (i)
Given,
Solution 5
In Δ RPQ and Δ RST
∠RTS = ∠QPS [given]
∠R = ∠R [common angle]
∠RST = ∠RQP [ Remaining angles]
Therefore Δ RPQ ~ Δ RTS [by AAA rule]
Solution 6
Since Δ ABE ≅ Δ ACD
Therefore AB = AC (1)
AD = AE (2)
Now, in Δ ADE and Δ ABC,
Dividing equation (2) by (1)
Solution 7
(i)
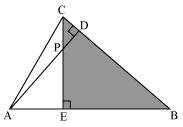
In Δ AEP and Δ CDP
Since ∠CDP = ∠AEP = 90°
∠CPD = ∠APE (vertically opposite angles)
∠PCD = ∠PAE (remaining angle)
Therefore by AAA rule,
Δ AEP ~ Δ CDP
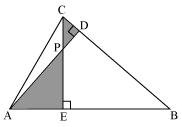
(ii)
In Δ ABD and Δ CBE
∠ADB = ∠CEB = 90°
∠ABD = ∠CBE (common angle)
∠DAB = ∠ECB (remaining angle)
Therefore by AAA rule
Δ ABD ~ Δ CBE
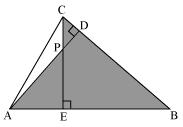
(iii)
In Δ AEP and Δ ADB
∠AEP = ∠ADB = 90°
∠PAE = ∠DAB (common angle)
∠APE = ∠ABD (remaining angle)
Therefore by AAA rule
Δ AEP ~ Δ ADB
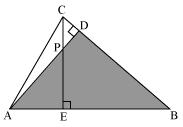
(iv)
In Δ PDC and Δ BEC
∠PDC = ∠BEC = 90°
∠PCD = ∠BCE (common angle)
∠CPD = ∠CBE
Therefore by AAA rule
Δ PDC ~ Δ BEC
Solution 8
Δ ABE and Δ CFB
∠A = ∠C (opposite angles of a parallelogram)
∠AEB = ∠CBF (Alternate interior angles AE || BC)
∠ABE = ∠CFB (remaining angle)
Therefore Δ ABE ~ Δ CFB (by AAA rule)
Solution 9
In Δ ABC and Δ AMP
∠ABC = ∠AMP = 90
∠A = ∠A (common angle)
∠ACB = ∠APM (remaining angle)
Therefore Δ ABC ~ Δ AMP (by AAA rule)
Solution 10
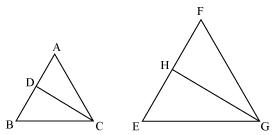
Since Δ ABC ~ Δ FEG
Therefore ∠A = ∠F
∠B = ∠E
As, ∠ACB = ∠FGE
Therefore ∠ACD = ∠FGH (angle bisector)
And ∠DCB = ∠HGE (angle bisector)
Therefore Δ ACD ~ Δ FGH (by AAA rule)
And Δ DCB ~ Δ HGE (by AAA rule)
and ∠ACD = ∠FGH
Therefore Δ DCA ~ Δ HGF (by SAS rule)
Solution 11
In Δ ABD and Δ ECF,
Given that AB = AC (isosceles triangles)
So, ∠ABD = ∠ECF
∠ADB = ∠EFC = 90
∠BAD = ∠CEF
Therefore ΔABD ~ ΔECF (by AAA rule)
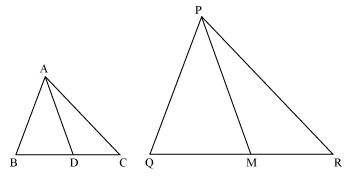
Solution 12
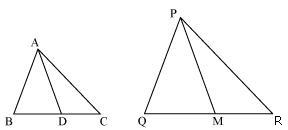
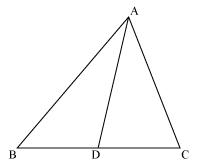
Median divides opposite side.
Therefore Δ ABD ~ Δ PQM (by SSS rule)
Therefore ∠ABD = ∠PQM (corresponding angles of similar triangles)
Therefore Δ ABC ~ Δ PQR (by SAS rule)
Solution 13
In Δ ADC and Δ BAC
Given that ∠ADC = ∠BAC
∠ACD = ∠BCA (common angle)
∠CAD = ∠CBA (remaining angle)
Hence, Δ ADC ~ Δ BAC [by AAA rule]
So, corresponding sides of similar triangles will be proportional to each other
Solution 14
Solution 15
m
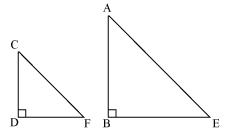
Let AB be a tower
CD be a pole
Shadow of AB is BE
Shadow of CD is DF
The light rays from sun will fall on tower and pole at same angle and at the same time.
So, ∠DCF = ∠BAE
And ∠DFC = ∠BEA
∠CDF = ∠ABE (tower and pole are vertical to ground)
Therefore Δ ABE ~ Δ CDF
So, height of tower will be 42 meters.
Solution 16
Since Δ ABC ~ ΔPQR
So, their respective sides will be in proportion
Also, ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R (2)
Since, AD and PM are medians so they will divide their opposite sides in equal halves.
From equation (1) and (3)
So, we had observed that two respective sides are in same proportion in both triangles and also angle included between them is respectively equal
Hence, Δ ABD ~ Δ PQM (by SAS rule)