Class 10 NCERT Solutions Maths Chapter 1 - Real Numbers
Real Numbers Exercise Ex. 1.1
Solution 1
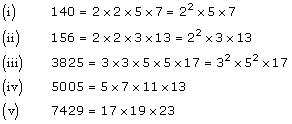
Concept Insight: Since the given number needs to be expressed as the product of prime factors so in order to solve this problem knowing prime numbers is required. Do not forget to put the exponent in case a prime number is repeating.
Solution 2
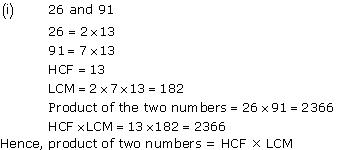


Concept Insight: HCF is the product of common prime factors raised to least power, while LCM is product of prime factors raised to highest power. HCF is always a factor of the LCM.
Do not skip verification product of two numbers = HCF x LCM as it can help in cross checking the answer.
Solution 3

Concept Insight: HCF is the product of common prime factors of all three numbers raised to least power, while LCM is product of prime factors of all here raised to highest power. Use the fact that HCF is always a factor of the LCM to verify the answer. Note HCF of (a,b,c) can also be calculated by taking two numbers at a time i.e HCF (a,b) and then HCF (b,c) .
Solution 4
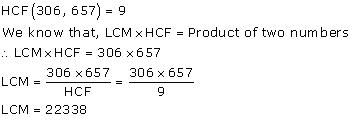
Concept Insight: This problem must be solved using product of two numbers = HCF x LCM rather then prime factorisation
Solution 5
If any number ends with the digit 0, it should be divisible by 10 or in other words its prime factorisation must include primes 2 and 5 both
Prime factorisation of 6n = (2 x 3)n
By Fundamental Theorem of Arithmetic Prime factorisation of a number is unique. So 5 is not a prime factor of 6n.
Hence, for any value of n, 6n will not be divisible by 5.
Therefore, 6n cannot end with the digit 0 for any natural number n.
Concept Insight: In order solve such problems the concept used is if a number is to end with zero then it must be divisible by 10 and the prime factorisation of a number is unique.
Solution 6
Numbers are of two types - prime and composite. Prime numbers has only two factors namely 1 and the number itself whereas composite numbers have factors other than 1 and itself.
It can be observed that
7 x 11 x 13 + 13 = 13 x (7 x 11 + 1) = 13 x (77 + 1)
= 13 x 78
= 13 x 13 x 6
The given expression has 6 and 13 as its factors. Therefore, it is a composite number.
7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 = 5 x (7 x 6 x 4 x 3 x 2 x 1 + 1)
= 5 x (1008 + 1)
= 5 x 1009
1009 cannot be factorised further. Therefore, the given expression has 5 and 1009 as its factors. Hence, it is a composite number.
Concept Insight: Definition of prime numbers and composite numbers is used. Do not miss the reasoning.
Solution 7
It can be observed that Ravi and Sonia does not take same amount of time Ravi takes lesser time than Sonia for completing 1 round of the circular path.
As they are going in the same direction, they will meet again at the same time when Ravi will have completed 1 round of that circular path with respect to Sonia.
i.e When Sonia completes one round then ravi completes 1.5 rounds. So they will meet first time at the time which is a common multiple of the time taken by them to complete 1 round
i.e LCM of 18 minutes and 12 minutes.
Now
18 = 2 x 3 x 3 = 2 x 32
And, 12 = 2 x 2 x 3 = 22 x 3
LCM of 12 and 18 = product of factors raised to highest exponent =
22 x 32 = 36
Therefore, Ravi and Sonia will meet together at the starting point after 36 minutes.
Concept Insight: In order to solve the word problems first step is to interpret the problem and identify what is to be determined. The problem asks for simultaneous reoccurrence of events so we need to find LCM. The key word for simultaneous reoccurrence of events is LCM. Do not forget to write the final answer.
Real Numbers Exercise Ex. 1.2
Solution 1
Let us assume, on the contrary that ![]() is a rational number.
is a rational number.
Therefore, we can find two integers a,b (b # 0) such that ![]() =
= ![]()
Where a and b are co-prime integers.
Therefore, a2 is divisible by 5 then a is also divisible by 5.
So a = 5k, for some integer k.
This means that b2 is divisible by 5 and hence, b is divisible by 5.
This implies that a and b have 5 as a common factor.
And this is a contradiction to the fact that a and b are co-prime.
Concept Insight: There are various ways of proving in mathematics proof by contradiction is one of them. In this approach we assume something which is contrary to what needs to be proved and arrive at a fact which contradicts something which is true in general. Key result used here is "If P is a prime number and it divides a2 then it divides a as well".
Solution 2
Therefore, we can find two integers a, b (b ![]() 0) such that
0) such that
Concept Insight: This problem is solved using proof by contradiction. The key concept used is if p is prime number then is irrational. Do not prove this question by assuming sum of rational and irrational is irrational.
Solution 3
Concept Insight: This problem is solved using proof by contradiction. The key concept used is if p is prime number then is irrational.Do not prove this question by assuming sum or product of rational and irrational is irrational.






