Class 10 NCERT Solutions Maths Chapter 2 - Polynomials
Ex. 2.1
Ex. 2.2
Polynomials Exercise Ex. 2.1
Solution 1
(i) The graph of P(x) does not cut the x-axis at all . So, the number of zeroes is 0.
(ii) The graph of P(x) intersects the x-axis at only 1 point.
So, the number of zeroes is 1.
(iii) The graph of P(x) intersects the x-axis at 3 points.
So, the number of zeroes is 3.
(iv) The graph of P(x) intersects the x-axis at 2 points.
So, the number of zeroes is 2.
(v) The graph of P(x) intersects the x-axis at 4 points.
So, the number of zeroes is 4.
(vi) The graph of P(x) intersects the x-axis at 3 points.
So, the number of zeroes is 3.
Concept insight: Since the polynomial p(x) given here is a polynomial in variable x, so to find the number of zeroes, we look at the number of points where the graph intersects or touches the x-axis and not the y-axis.
At all these points where the graph intersects x axis the value of the polynomial y = p(x) will be zero.
(ii) The graph of P(x) intersects the x-axis at only 1 point.
So, the number of zeroes is 1.
(iii) The graph of P(x) intersects the x-axis at 3 points.
So, the number of zeroes is 3.
(iv) The graph of P(x) intersects the x-axis at 2 points.
So, the number of zeroes is 2.
(v) The graph of P(x) intersects the x-axis at 4 points.
So, the number of zeroes is 4.
(vi) The graph of P(x) intersects the x-axis at 3 points.
So, the number of zeroes is 3.
Concept insight: Since the polynomial p(x) given here is a polynomial in variable x, so to find the number of zeroes, we look at the number of points where the graph intersects or touches the x-axis and not the y-axis.
At all these points where the graph intersects x axis the value of the polynomial y = p(x) will be zero.
Polynomials Exercise Ex. 2.2
Solution 1
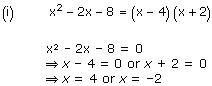
So, the zeroes of x² - 2x - 8 are 4 and -2.
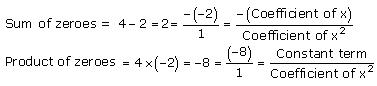
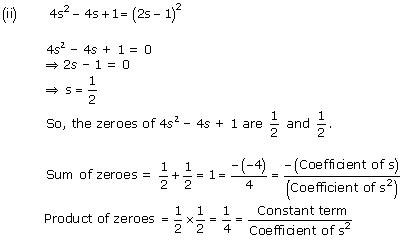
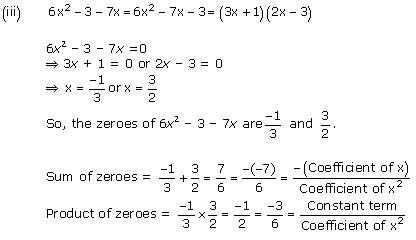
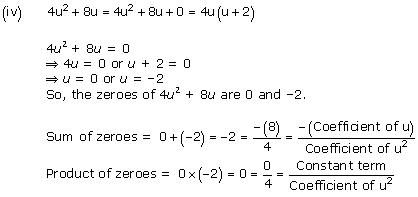
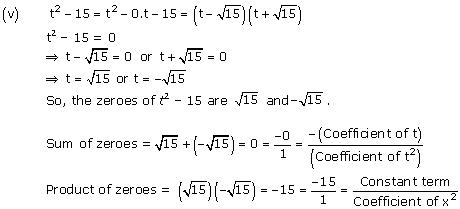
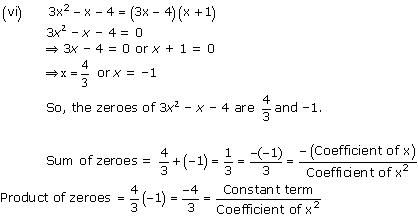
Concept insight: The zero of a polynomial is that value of the variable which when substituted in the polynomial makes its value 0.
When a quadratic polynomial is equated to 0, then the values of the variable obtained are the zeroes of that polynomial. The relationship between the zeroes of a quadratic polynomial with its coefficients is very important. Also, while verifying the above relationships, be careful about the signs of the coefficients.
Solution 2
(i) Let the required polynomial be ax² + bx + c, and let its zeroes ![]() and
and ![]()
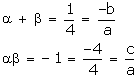
If a = 4k, then b = -k, c = -4k
Therefore, the quadratic polynomial is k(4x 2 - x - 4), where k is a real number .
One quadratic polynomial which fits the given condition is 4x 2 - x - 4, when k = 1.
(ii) Let the polynomial be ax² + bx + c, and let its zeroes be and
and 
(ii) Let the polynomial be ax² + bx + c, and let its zeroes be

One quadratic polynomial which fits the given condition is 3x2 - 3 x + 1, when k = 1.
x + 1, when k = 1.
(iii) Let the polynomial be ax² + bx + c, and let its zeroes be  and
and 
One quadratic polynomial which fits the given condition is x2 +  x, when k = 1.
x, when k = 1.
(iv) Let the polynomial be ax² + bx + c, and let its zeroes be  and
and 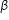
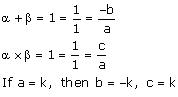
Therefore, the quadratic polynomial is k(x² - x + 1),where k is a real number .
One quadratic polynomial which fits the given condition is x² - x + 1, when k = 1.
(v) Let the polynomial be ax² + bx + c, and its zeroes be and
and 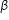
(v) Let the polynomial be ax² + bx + c, and its zeroes be
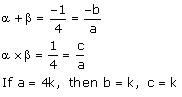
Therefore, the quadratic polynomial is k(4x² + x + 1),where k is a real number .
One quadratic polynomial which fits the given condition is 4x² + x + 1,when k = 1.
(vi) Let the polynomial be ax² + bx + c.
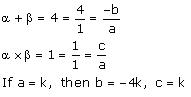
(vi) Let the polynomial be ax² + bx + c.
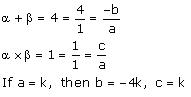
Therefore, the quadratic polynomial is k(x² - 4x + 1),where k is a real number .
One quadratic polynomial which fits the given condition is x² - 4x + 1,when k = 1.
Concept insight: Since the sum and product of zeroes gives 2 relations between three unknowns so we assign a value to the variable a and obtain other values.
Alternatively If the sum and the product of the zeroes of a quadratic polynomial is given then polynomial is given by x2 - (sum of the roots)x + product of the roots, where k is a constant. And the simplest polynomial will be the one in which k = 1.
Concept insight: Since the sum and product of zeroes gives 2 relations between three unknowns so we assign a value to the variable a and obtain other values.
Alternatively If the sum and the product of the zeroes of a quadratic polynomial is given then polynomial is given by x2 - (sum of the roots)x + product of the roots, where k is a constant. And the simplest polynomial will be the one in which k = 1.

