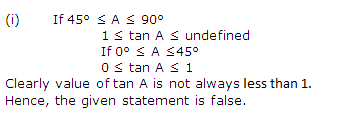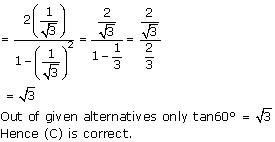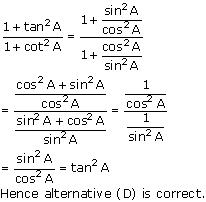Class 10 NCERT Solutions Maths Chapter 8 - Introduction to Trigonometry
Ex. 8.1
Ex. 8.2
Ex. 8.3
Introduction to Trigonometry Exercise Ex. 8.1
Solution 1
In ![]() ABC by applying Pythagoras theorem
ABC by applying Pythagoras theorem
AC2 = AB2 + BC2
= (24)2 + (7)2
= 576 + 49
= 625
AC = = 25 cm


![]()
Solution 2
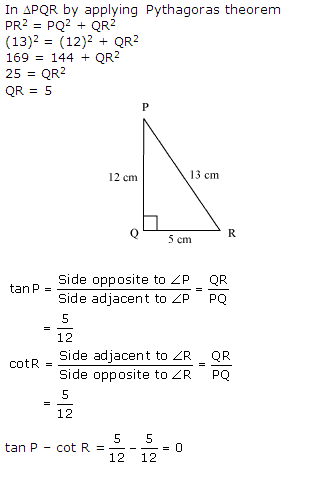
Solution 3

Solution 4
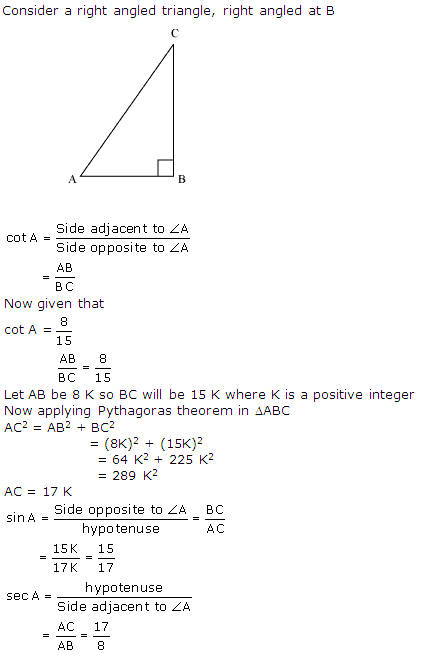
Solution 5

Solution 6
Since ![]() A and
A and ![]() B are acute angles, then
B are acute angles, then ![]() C is a right angle.
C is a right angle.
cos A = cos B .... given
AC/AB = BC/AB
AC = BC
![]() B =
B =![]() A .... angles opposite to equal sides are equal in length.
A .... angles opposite to equal sides are equal in length.
Solution 7
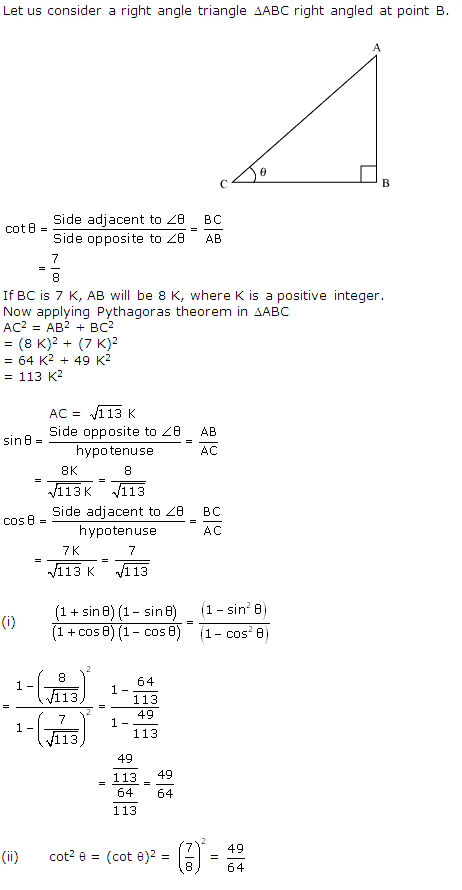
Solution 8

Solution 9
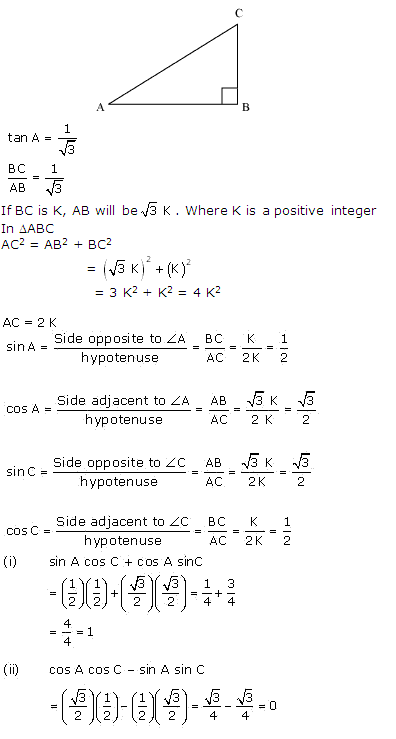
Solution 10
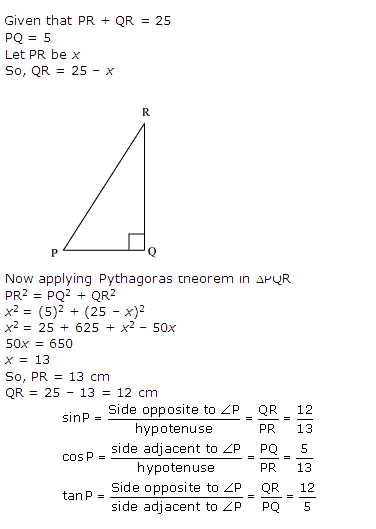
Solution 11
Introduction to Trigonometry Exercise Ex. 8.2
Solution 1
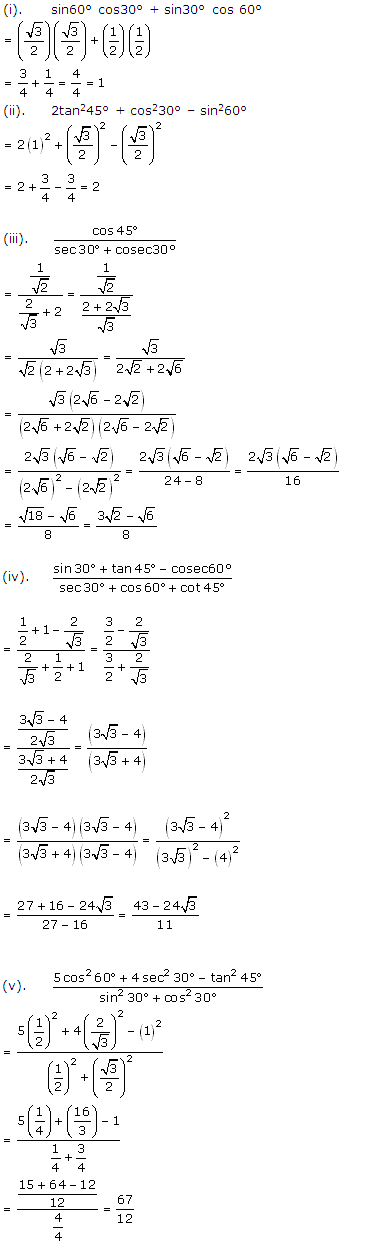
Solution 2

Solution 3
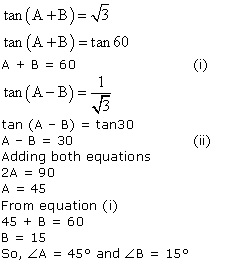
Solution 4
Introduction to Trigonometry Exercise Ex. 8.3
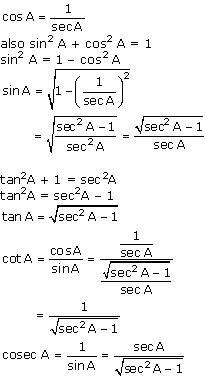
Solution 1
We know that
Solution 2
We know that
Solution 3
(i) 9sec2A - 9tan2A
= 9(sec2A - tan2A)
= 9 (1) (as sec2A - tan2A = 1)
= 9
Hence alternative (B) is correct.
(ii) (1 + tanθ + secθ) (1 + cotθ - cosecθ) 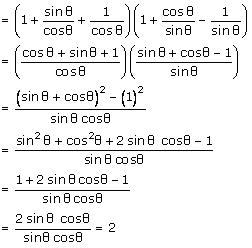
Hence alternative (C) is correct.
(iii) (secA + tanA) (1 - sinA) 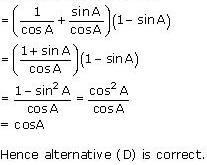
(iv)
Solution 4