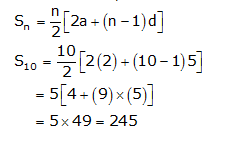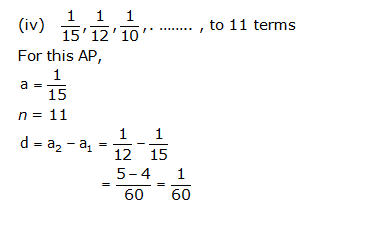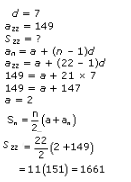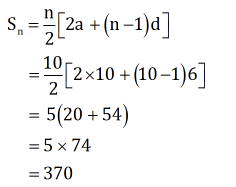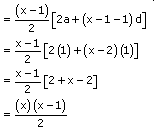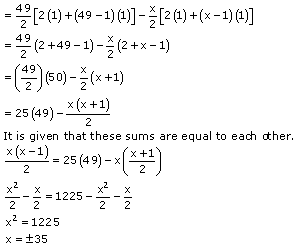NCERT Solutions for Class 10 Maths Chapter 5 - Arithmetic Progressions
Does the sound of Class 10 Maths intrigue you? Or, does it scare you away? It’s not easy to handle the Board pressure for Class 10. But, we can definitely help you tackle the syllabus for CBSE Class 10 Maths. Scoring more marks in Mathematics CBSE Class 10 has never been this easy before. You just have to start by referring to the CBSE class 10 maths notes.
Our study materials for CBSE Class 10 Mathematics are created by subject experts who teach students Maths. Our materials will help you to score high marks in your Mathematics examination as we focus on providing solutions which simplify the complex fundamentals of a subject. At TopperLearning, we believe in providing quality solutions at a low cost, and we strictly follow the latest CBSE syllabus; our study materials are revised from time to time. Our TopperLearning packages involve all the study resources for CBSE Class 10 such as solved question papers, video lessons and revision notes which will help you to score high marks. We also provide free NCERT and RD Sharma textbook solutions which provide students with step-by-step solutions.
Chapter 5 - Arithmetic Progressions Exercise Ex. 5.1
Solution 1
Solution 2
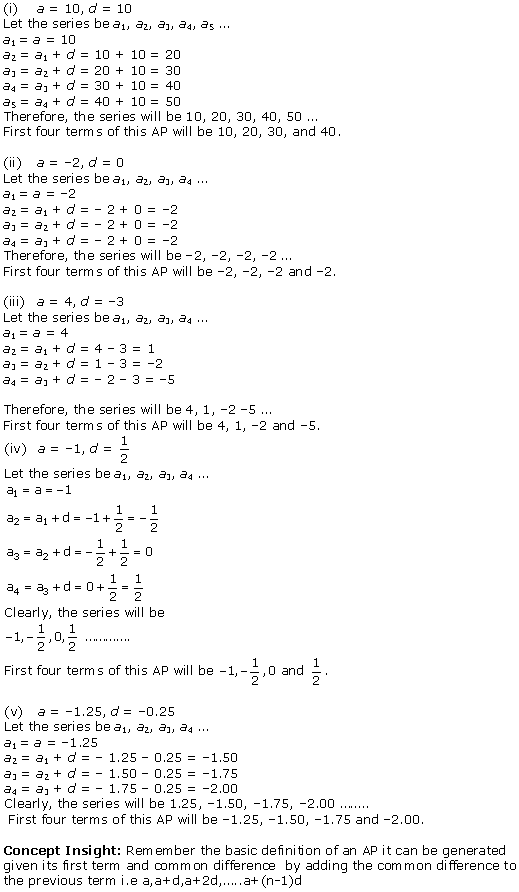
Solution 3
Solution 4
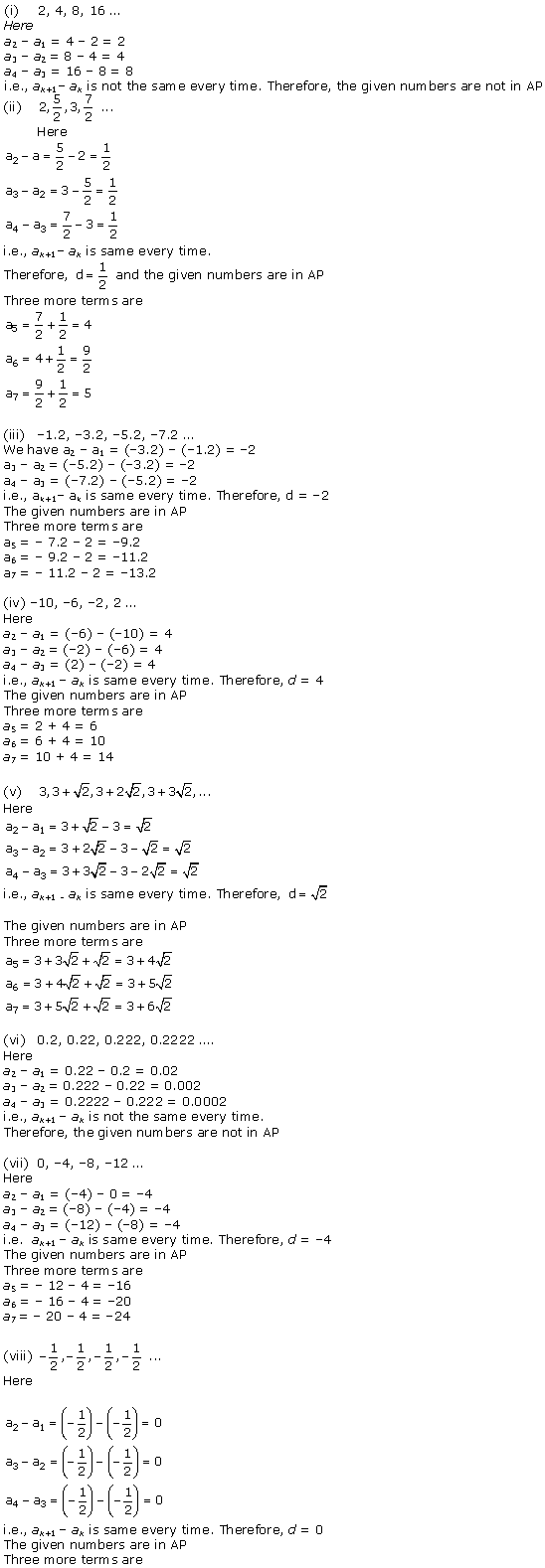
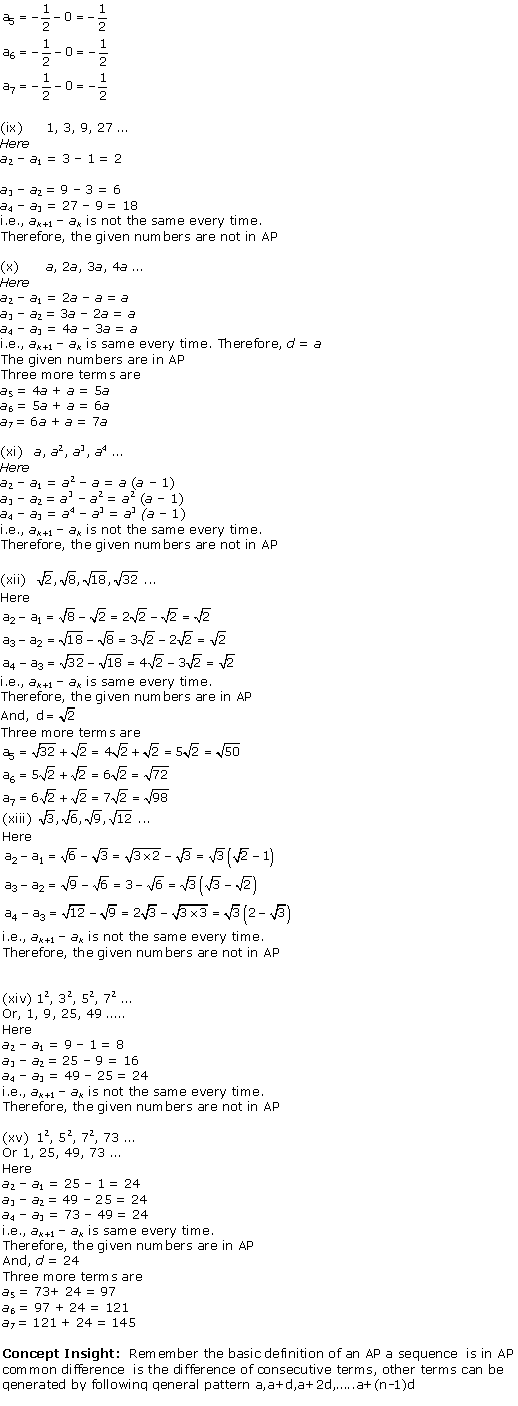
Chapter 5 - Arithmetic Progressions Exercise Ex. 5.2
Solution 1
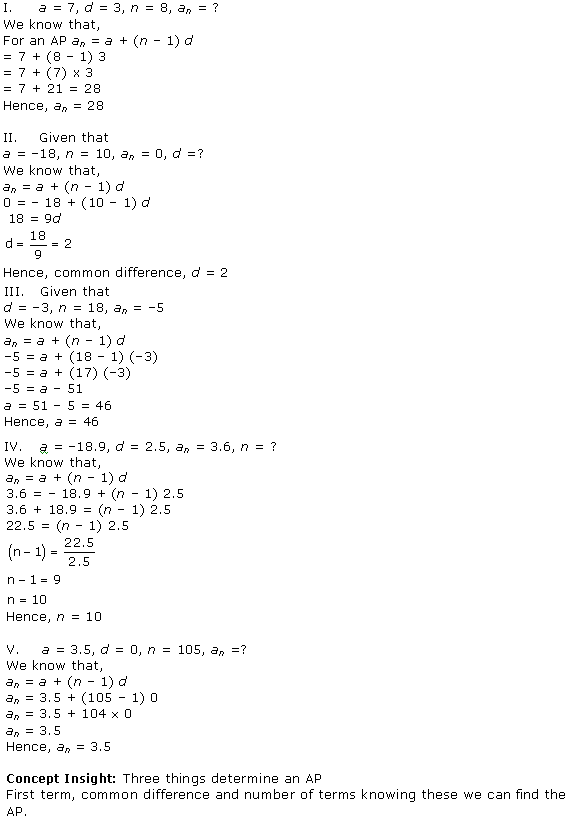
Solution 2
We have to find the 30th term and 11th term in I and II respectively.
Solution 3
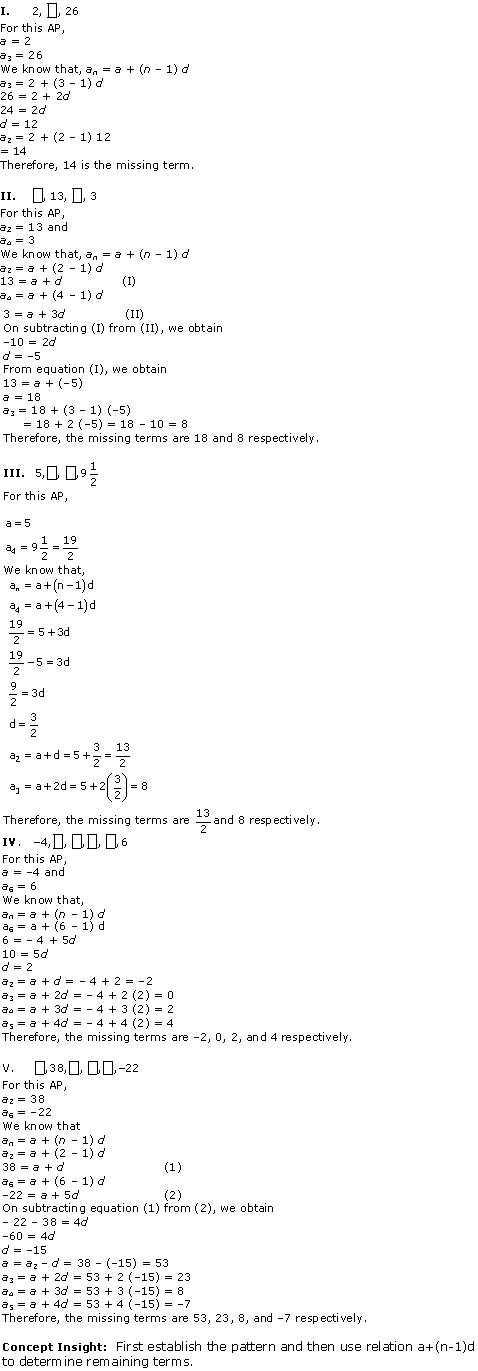
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
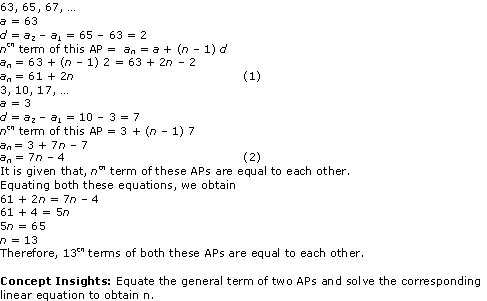
Solution 16
Solution 17
Solution 18
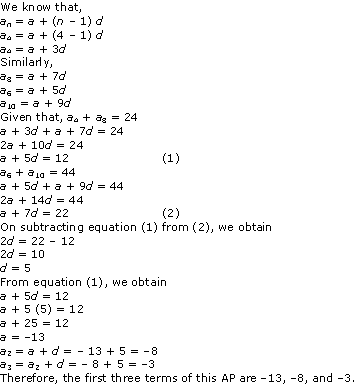
Solution 19
Solution 20
Chapter 5 - Arithmetic Progressions Exercise Ex. 5.3
Solution 1
(i) 2, 7, 12 ,…, to 10 terms
For this AP,
a = 2
d = a2 – a1 = 7 – 2 = 5
n = 10
We know that,
(ii) –37, –33, –29 ,…, to 12 terms
For this AP,
a = –37
d = a2 – a1 = (–33) – (–37)
= – 33 + 37 = 4
n = 12
We know that,
(iii) 0.6, 1.7, 2.8 ,…, to 100 terms
For this AP,
a = 0.6
d = a2 – a1 = 1.7 – 0.6 = 1.1
n = 100
We know that,
Solution 2
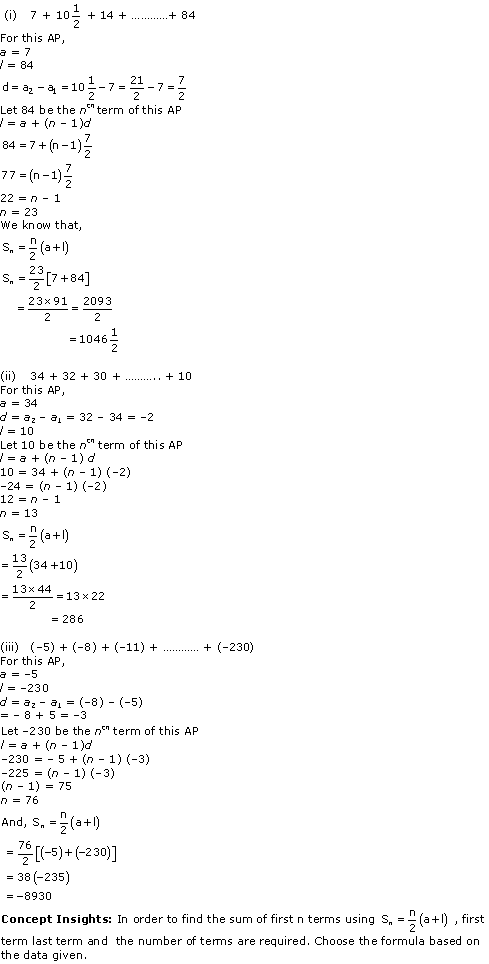
Solution 3
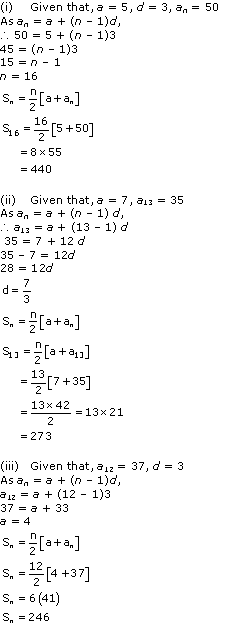
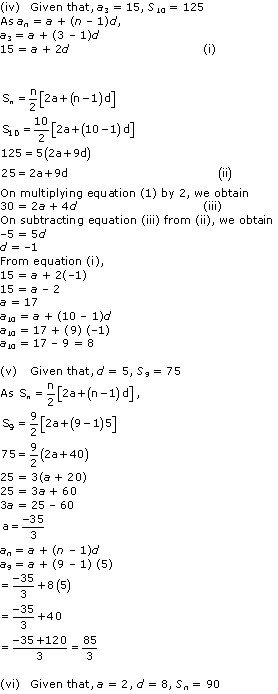
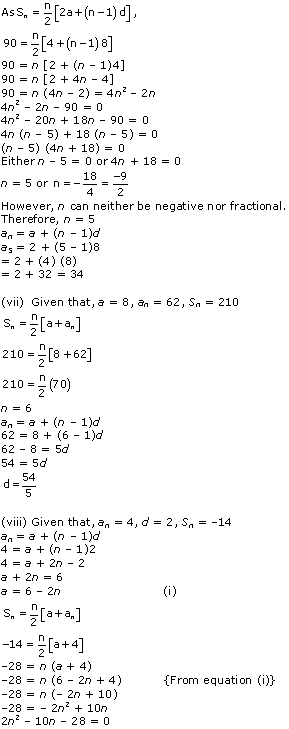
Solution 4
Solution 5
Solution 6
Solution 7
Solution 8
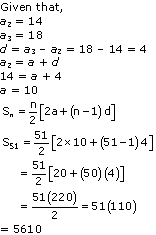
Solution 9
Solution 10
(i)
(ii)
Solution 11
Solution 12
Solution 13
Solution 14
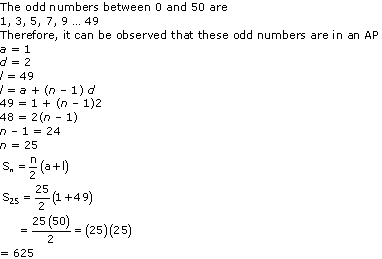
Solution 15
Solution 16
Solution 17
Solution 18
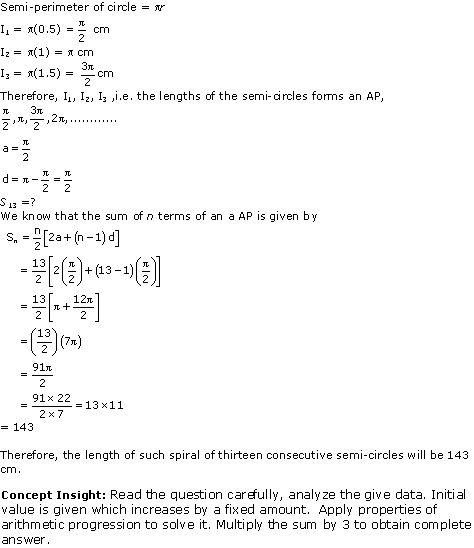
Solution 19
Solution 20
In a potato race, a bucket is placed at the starting point, which is 5m from the first potato and other potatoes are placed 3m apart in a straight line. There are ten potatoes in the line.
So, we get the series as
5, 8, 11, 14, ........
Here, a= 5 and d = 8 - 5 = 11 - 8= 3
the difference between the two consecutive terms are same.
So, this is an arithmetic Progression.
According to the condition, we get the series as
5 + 5 , 8 + 8, 11 + 11, .....
10, 16, 22, ..............
Here a = 10 and d = 16 - 10 = 6
the difference between the two consecutive terms are same.
So, this is an arithmetic Progression.
The total distance the competitor has to run is given by,
Therefore the total distance the competitor has to run is 370 m.
Chapter 5 - Arithmetic Progressions Exercise Ex. 5.4
Solution 1
Solution 2
Solution 3
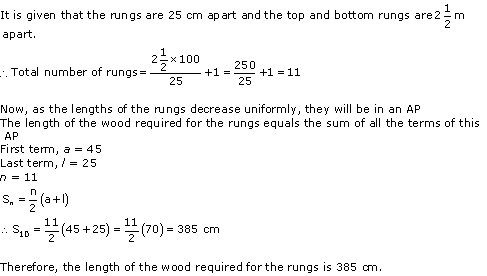
Solution 4
The number of houses was 1, 2, 3, ..... 49.
It can be observed that the number of houses are in an AP having a as 1 and d also as 1.
Let us assume that the number of xth house was like this.
We know that,
Sum of number of houses preceding xth house = Sx-1
Sum of number of houses preceding xth house = S49 - Sx
However, the house numbers are positive integers.
The value of x will be 35 only.
Therefore, house number 35 is such that the sum of the numbers of houses preceding
the house numbered 35 is equal to the sum of the numbers of the houses following it.
Solution 5
Why to choose our CBSE Class 10 Maths Study Materials?
- Contain 950+ video lessons, 200+ revision notes, 8500+ questions and 15+ sample papers
- Based on the latest CBSE syllabus
- Free textbook solutions & doubt-solving sessions
- Ideal for quick revision
- Help score more marks in the examination
- Increase paper-solving speed and confidence with weekly tests
Kindly Sign up for a personalised experience
- Ask Study Doubts
- Sample Papers
- Past Year Papers
- Textbook Solutions
Sign Up
Verify mobile number
Enter the OTP sent to your number
Change