Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

Class 8 MAHARASHTRA STATE TEXTBOOK BUREAU Solutions Maths Chapter 5: Expansion formulae

Expansion formulae Exercise Ex. 5.1

Solution 1(1)

We know that,

(x + a)(x + b) = x2 + (a + b)x + ab

⇒ (a + 2)(a - 1) = a2 + [2 + (-1)]a + 2 × (-1)

 = a2 + (2 - 1)a - 2

 = a2 + a - 2

Solution 1(2)

We know that,

(x + a)(x + b) = x2 + (a + b)x + ab

⇒ (m - 4)(m + 6) = m2 + [(-4) + 6]m + (-4) × 6

 = m2 + 2m - 24

Solution 1(3)

We know that,

(x + a)(x + b) = x2 + (a + b)x + ab

⇒ (p + 8)(p - 3) = p2 + [8 + (-3)]p + 8 × (-3)

 = p2 + 5p - 24

Solution 1(4)

We know that,

(x + a)(x + b) = x2 + (a + b)x + ab

⇒ (13 + x)(13 - x) = 132 + [x + (-x)]13 + x × (-x)  

 = 169 + 0 × 13 - x2

 = 169 - x2

Solution 1(5)

We know that,

(x + a)(x + b) = x2 + (a + b)x + ab

⇒ (3x + 4y)(3x + 5y)= (3x)2 + (4y + 5y)3x + 4y × 5y  

 = 9x2 + 9y × 3x + 20y2

 = 9x2 + 27xy + 20y2

Solution 1(6)

We know that,

(x + a)(x + b) = x2 + (a + b)x + ab

⇒ (9x - 5t)(9x + 3t) = (9x)2 + (-5t + 3t)9x + (-5t) × 3t  

 = 81x2 - 2t × 9x - 15t2

 = 81x2 - 18xt - 15t2

Solution 1(7)

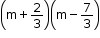
begin mathsize 12px style open parentheses straight m plus 2 over 3 close parentheses open parentheses straight m minus 7 over 3 close parentheses end style 

We know that,

(x + a)(x + b) = x2 + (a + b)x + ab

 

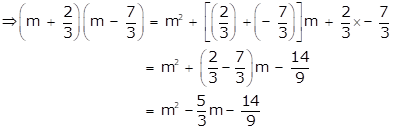
Solution 1(8)

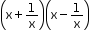
begin mathsize 12px style open parentheses straight x plus 1 over straight x close parentheses open parentheses straight x minus 1 over straight x close parentheses end style 

We know that,

(x + a)(x + b) = x2 + (a + b)x + ab

 

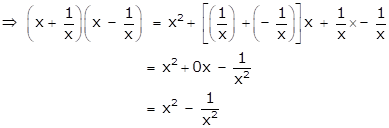
Solution 1(9)

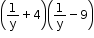
begin mathsize 12px style open parentheses 1 over straight y plus 4 close parentheses open parentheses 1 over straight y minus 9 close parentheses end style 

We know that,

(x + a)(x + b) = x2 + (a + b)x + ab

 

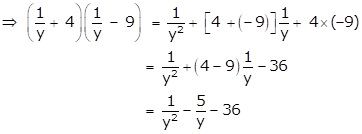
Expansion formulae Exercise Ex. 5.2

Solution 1

We know that (a + b)3 = a3 + 3a2b + 3ab2 + b3

Comparing (k + 4)3 with (a + b)3, we get

a = k and b = 4

∴ (k + 4)3 = k3 + 3 × k2 × 4 + 3 × k × 42 + 43

 = k3 + 12k2 + 3 × k × 16 + 64

 = k3 + 12k2 + 48k + 64

Solution 2

We know that (a + b)3 = a3 + 3a2b + 3ab2 + b3

Comparing (7x + 8y)3 with (a + b)3, we get

a = 7x and b = 8y

∴ (7x + 8y)3 = (7x)3 + 3 × (7x)2 × 8y + 3 × 7x × (8y)2 + (8y)3

 = 343x3 + 3 × 49x2 × 8y + 3 × 7x × 64y2 + 512y3

 = 343x3 + 147x2 × 8y + 21x × 64y2 + 512y3

 = 343x3 + 1176x2y + 1344xy2 + 512y3

Solution 3

We know that (a + b)3 = a3 + 3a2b + 3ab2 + b3

Comparing (7 + m)3 with (a + b)3, we get

a = 7 and b = m

∴ (7 + m)3 = (7)3 + 3 × (7)2 × m + 3 × 7 × m2 + m3

 = 343+ 3 × 49 × m + 3 × 7 × m2 + m3

 = 343+ 147m + 21m2 + m3

Solution 4

We know that (a + b)3 = a3 + 3a2b + 3ab2 + b3

Comparing 523 = (50 + 2)3 with (a + b)3, we get

a = 50 and b = 2

∴ 523 = 503 + 3 × (50)2 × 2 + 3 × 50 × 22 + 23

 = 125000+ 3 × 2500 × 2 + 3 × 50 × 4 + 8

 = 125000+ 6 × 2500 + 150 × 4 + 8

 = 125000+ 15000 + 600 + 8

 = 140608

Solution 5

We know that (a + b)3 = a3 + 3a2b + 3ab2 + b3

Comparing 1013 = (100 + 1)3 with (a + b)3, we get

a = 100 and b = 1

∴ 1013 = 1003 + 3 × (100)2 × 1 + 3 × 100 × 1 + 13

= 1003 + 3 × (100)2 × 1 + 3 × 100 × 1 + 13

= 1000000 + 3 × 10000 + 300 + 1

= 1030301

Solution 6

We know that (a + b)3 = a3 + 3a2b + 3ab2 + b3

Comparing 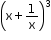begin mathsize 12px style open parentheses straight x plus 1 over straight x close parentheses cubed end style with (a + b)3, we get

a = x and b =  

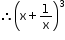
begin mathsize 12px style therefore open parentheses straight x plus 1 over straight x close parentheses cubed end style 

= x3 + 3 × x2 ×  + 3 × x × +  

= x3 + 3x +  +  

Solution 7

We know that (a + b)3 = a3 + 3a2b + 3ab2 + b3

Comparing 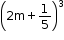begin mathsize 12px style open parentheses 2 straight m plus 1 fifth close parentheses cubed end style with (a + b)3, we get

a = 2m and b =  

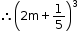
 begin mathsize 12px style therefore open parentheses 2 straight m plus 1 fifth close parentheses cubed end style 

= (2m)3 + 3 × (2m)2 ×  + 3 × 2m × +  

= 8m3 + 3 × 4m2 ×  + 6m ×   +  

= 8m3 + m2 +   m +  

Solution 8

We know that (a + b)3 = a3 + 3a2b + 3ab2 + b3

Comparing 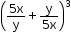begin mathsize 12px style open parentheses fraction numerator 5 straight x over denominator straight y end fraction plus fraction numerator straight y over denominator 5 straight x end fraction close parentheses cubed end style with (a + b)3, we get

a =  and b =  

 

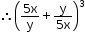
begin mathsize 12px style therefore open parentheses fraction numerator 5 straight x over denominator straight y end fraction plus fraction numerator straight y over denominator 5 straight x end fraction close parentheses cubed end style 

 + 3 × ×  + 3 ×  × +  

=  + 3 ×  ×  + 3 ×  ×  +  

=  + 3 ×  +  +  

=  +  +  +  

Expansion formulae Exercise Ex. 5.3

Solution 1(1)

We know that (a - b)3 = a3- 3a2b + 3ab2- b3

Comparing (2m - 5)3 with (a - b)3, we get

a = 2m and b = 5 

∴ (2m - 5)3= (2m)3 - 3 × (2m)2 × 5 + 3 × 2m × 52 - 53 

 = 8m3 - 3 × 4m2 × 5 + 3 × 2m × 25 - 125

 = 8m3  - 60m2 + 150m - 125

Solution 1(2)

We know that (a - b)3 = a3- 3a2b + 3ab2- b3

Comparing (4 - p)3 with (a - b)3, we get

a = 4 and b = p 

∴ (4 - p)3= 43 - 3 × 42 × p + 3 × 4 × p2- p3

 = 64  - 3 × 16p + 12p2 - p3

 = 64  - 48p + 12p2 - p3

Solution 1(3)

We know that (a - b)3 = a3- 3a2b + 3ab2- b3

Comparing (7x - 9y)3 with (a - b)3, we get

a = 7x and b = 9y 

∴ (7x - 9y)3= (7x)3 - 3 × (7x)2 × 9y + 3 × 7x × (9y)2- (9y)3 

  =  343x3 - 3 × 49x2 × 9y + 3 × 7x × 81y2- 729y3

 = 343x3 - 147x2 × 9y + 21x × 81y2- 729y3

 = 343x3 - 1323x2y + 1701xy2- 729y3

Solution 1(4)

We know that (a - b)3 = a3- 3a2b + 3ab2- b3

Comparing (58)3 = (60 - 2)3 with (a - b)3, we get

a = 60 and b = 2 

∴ (60 - 2)3= (60)3 - 3 × (60)2 × 2 + 3 × 60 × 22- 23

 =  216000 - 3 × 3600 × 2 + 180 × 4 - 8

 = 216000 - 21600 + 720 - 8

 = 195112

Solution 1(5)

We know that (a - b)3 = a3- 3a2b + 3ab2- b3

Comparing (198)3 = (200 - 2)3 with (a - b)3, we get

a = 200 and b = 2 

∴ (200 - 2)3= (200)3 - 3 × (200)2 × 2 + 3 × 200 × 22- 23 

 =  8000000 - 3 × 40000 × 2 + 600 × 4 - 8

 = 8000000 - 240000 + 2400 - 8

 = 7762392

Solution 1(6)

We know that (a - b)3 = a3- 3a2b + 3ab2- b3

Comparing 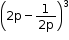begin mathsize 12px style open parentheses 2 straight p minus fraction numerator 1 over denominator 2 straight p end fraction close parentheses cubed end style with (a - b)3, we get

a = 2p and b =  

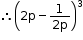
begin mathsize 12px style therefore open parentheses 2 straight p minus fraction numerator 1 over denominator 2 straight p end fraction close parentheses cubed end style 

 = (2p)3- 3 × (2p)2 ×  + 3 × 2p ×  -  

 =  8p3- 3 × 4p2 ×  + 3 × 2p ×  -  

 = 8p3- 6p +  -  

Solution 1(7)

We know that (a - b)3 = a3- 3a2b + 3ab2- b3

Comparing 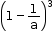begin mathsize 12px style open parentheses 1 minus 1 over straight a close parentheses cubed end style with (a - b)3, we get

a = 1 and b =  

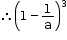
begin mathsize 12px style therefore open parentheses 1 minus 1 over straight a close parentheses cubed end style 

 = 13- 3 × 12 ×  + 3 × 1 ×  -  

 =  1-   + 3 ×  -  

 = 1-   +   -  

Solution 1(8)

We know that (a - b)3 = a3- 3a2b + 3ab2- b3

Comparing 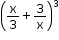begin mathsize 12px style open parentheses straight x over 3 plus 3 over straight x close parentheses cubed end style with (a - b)3, we get

a =  and b =  

 

=  

 

 

 

Solution 2(1)

We know that (a + b)3 = a3+ 3a2b + 3ab2+ b3 and

(a - b)3 = a3- 3a2b + 3ab2- b3

 

Consider,

(2a + b)3 = (2a)3 + 3 × (2a)2 × b + 3 × 2a × b2 +b3

 = 8a3 + 3 × 4a2b + 6ab2 + b3

 = 8a3 + 12a2b + 6ab2 + b3

 

Similarly, (2a - b)3 = 8a3 - 12a2b + 6ab2 - b3

 

∴ (2a + b)3 - (2a - b)3

 = 8a3 + 12a2b + 6ab2 + b3 - (8a3 - 12a2b + 6ab2 - b3)

 = 8a3 + 12a2b + 6ab2 + b3 - 8a3 + 12a2b - 6ab2 + b3

 = 12a2b + 12a2b + b3 + b3

 = 24a2b + 2b3  

Solution 2(2)

We know that (a + b)3 = a3+ 3a2b + 3ab2+ b3 and

(a - b)3 = a3- 3a2b + 3ab2- b3

 

Consider,

(3r - 2k)3

= (3r)3 - 3 × (3r)2 × 2k + 3 × 3r × (2k)2  -(2k)3

= 27r3 - 3 × 9r2 × 2k + 9r × 4k2 - 8k3

= 27r3 - 54r2k + 36rk2 - 8k3

 

Similarly, (3r + 2k)3 = 27r3 + 54r2k + 36rk2 + 8k3

 

∴ (3r - 2k)3 + (3r + 2k)3

 = 27r3 - 54r2k + 36rk2 - 8k3 + 27r3 + 54r2k + 36rk2 + 8k3

 = 27r3 + 27r3 + 36rk2 + 36rk2

 = 54r3 + 72rk2

Solution 2(3)

We know that (a + b)3 = a3+ 3a2b + 3ab2+ b3 and

(a - b)3 = a3- 3a2b + 3ab2- b3

 

Consider,

(4a - 3)3

= (4a)3 - 3 × (4a)2 × 3 + 3 × 4a × 32 -33

= 64a3 - 3 × 16a2 × 3 + 3 × 4a × 9 -27

= 64a3 - 144a2 + 108a -27

 

Similarly, (4a + 3)3 = 64a3 + 144a2 + 108a +27

 

(4a - 3)3 - (4a + 3)3

= 64a3 - 144a2 + 108a -27 - (64a3 + 144a2 + 108a +27)

= 64a3 - 144a2 + 108a -27 - 64a3 - 144a2 - 108a -27

= - 144a2 - 144a2 - 27 - 27

= -288a2 - 54

Solution 2(4)

We know that (a + b)3 = a3+ 3a2b + 3ab2+ b3 and

(a - b)3 = a3- 3a2b + 3ab2- b3

 

Consider,

(5x - 7y)3  

= (5x)3 - 3 × (5x)2 × 7y + 3 × 5x × (7y)2 -(7y)3

= 125x3 - 3 × 25x2 × 7y + 3 × 5x × 49y2 -343y3

= 125x3 - 525x2y + 735xy2 -343y3

 

Similarly, (5x + 7y)3 = 125x3 + 525x2y + 735xy2 +343y3

 

∴ (5x - 7y)3  + (5x + 7y)3

 = 125x3 - 525x2y + 735xy2 -343y3 + 125x3 + 525x2y + 735xy2 +343y3

 = 125x3 + 125x3 + 735xy2 + 735xy2

 = 250x3 + 1470xy2

Expansion formulae Exercise Ex. 5.4

Solution 1(1)

We know that (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca

 

Comparing (2p + q + 5)2 with (a + b + c)2, we get

a = 2p, b = q, c = 5

 

∴ (2p + q + 5)2

 = (2p)2 + q2 + 52 + 2 × 2p × q + 2 × q × 5 + 2 × 2p × 5

 = 4p2 + q2 + 25 + 4pq + 10q + 20p

Solution 1(2)

We know that (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca

 

Comparing (m + 2n + 3r)2 with (a + b + c)2, we get

a = m, b = 2n, c = 3r

 

∴ (m + 2n + 3r)2

 = m2 + (2n)2 + (3r)2 + 2 × m × 2n + 2 × 2n × 3r + 2 × m × 3r

 = m2 + 4n2 + 9r2 + 4mn + 12nr + 6mr 

Solution 1(3)

We know that (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca

 

Comparing (3x + 4y - 5p)2 with (a + b + c)2, we get

a = 3x, b = 4y, c = -5p

 

∴ (3x + 4y - 5p)2

 = (3x)2 + (4y)2 + (-5p)2 + 2 × 3x × 4y + 2 × 4y × (-5p) + 2 × 3x × (-5p)

 = 9x2 + 16y2 + 25p2 + 24xy - 40py - 30px

Solution 1(4)

We know that (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca

 

Comparing (7m - 3n - 4k)2 with (a + b + c)2, we get

a = 7m, b = -3n, c =  - 4k

 

∴ (7m - 3n - 4k)2

 = (7m)2 + (-3n)2 + (-4k)2 + 2 × 7m × (-3n) + 2 × (-3n) × (-4k) + 2 × 7m × (-4k)

 = 49m2 + 9n2 + 16k2 - 42mn + 24nk - 56mk

Solution 2(1)

We know that (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca

 

Comparing (x - 2y + 3)2 with (a + b + c)2, we get

a = x, b = -2y, c =  3

 

∴ (x - 2y + 3)2

 = x2 + (-2y)2 + 32 + 2 × x × (-2y) + 2 × (-2y) × 3 + 2 × x × 3

 = x2 + 4y2 + 9 - 4xy - 12y + 6x

 

(x + 2y - 3)2

= x2 + (2y)2 + (-3)2 + 2 × x × 2y + 2 × 2y × (-3) + 2 × x × (-3)

= x2 + 4y2 + 9 + 4xy - 12y - 6x

 

∴ (x - 2y + 3)2 + (x + 2y - 3)2

 = x2 + 4y2 + 9 - 4xy - 12y + 6x + x2 + 4y2 + 9 + 4xy - 12y - 6x

 = 2x2 + 8y2 + 18 - 24y

Solution 2(2)

We know that (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca

 

Comparing (3k - 4r - 2m)2 with (a + b + c)2

a = 3k, b = -4r, c = -2m

 

∴ (3k - 4r - 2m)

 = (3k)2 + (-4r)2 + (-2m)2 + 2 × 3k × (-4r) + 2 × (-4r) × (-2m) + 2 × 3k × (-2m)

 = 9k2 + 16r2 + 4m2 - 24kr + 16rm - 12km

 

Also, (3k + 4r - 2m)2

 = (3k)2 + (4r)2 + (-2m)2 + 2 × 3k × 4r + 2 × 4r × (-2m) + 2 × 3k × (-2m)

 = 9k2 + 16r2 + 4m2 + 24kr - 16rm - 12km

 

∴ (3k - 4r - 2m)2 - (3k + 4r - 2m)2

 = 9k2 + 16r2 + 4m2 - 24kr + 16rm - 12km - (9k2 + 16r2 + 8m2 + 24kr -  16rm - 12km)

 = 9k2 + 16r2 + 4m2 -24kr + 16rm - 12km - 9k2 - 16r2 - 4m2 - 24kr + 16rm + 12km

 = -24kr -24kr + 16rm + 16rm

 = -48kr + 32rm

Solution 2(3)

We know that (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca

 

Comparing (7a - 6b + 5c)2 with (a + b + c)2, we get

a = 7a, b = -6b, c = 5c

 

∴ (7a - 6b + 5c)2 

 = (7a)2 + (-6b)2 + (5c)2 + 2 × 7a × (-6b) + 2 × (-6b) × (5c) + 2 × 7a × 5c

 = 49a2 + 36b2 + 25c2 - 84ab - 60bc + 70ac

 

Also, (7a + 6b - 5c)2

 = (7a)2 + (6b)2 + (-5c)2 + 2 × 7a × 6b + 2 × 6b × (-5c) + 2 × 7a × (-5c)

 = 49a2 + 36b2 + 25c2 + 84ab - 60bc - 70ac

 

∴ (7a - 6b + 5c)2 + (7a + 6b - 5c)2

 = 49a2 + 36b2 + 25c2 - 84ab - 60bc + 70ac + 49a2 + 36b2 + 25c2 + 84ab - 60bc - 70ac

 = 49a2 + 49a2 + 36b2 + 36b2 + 25c2 + 25c2 - 60bc - 60bc

 = 98a2 + 72b2 + 50c2 - 120bc

My Class Videos Tests ₹ Plans Ask a Doubt