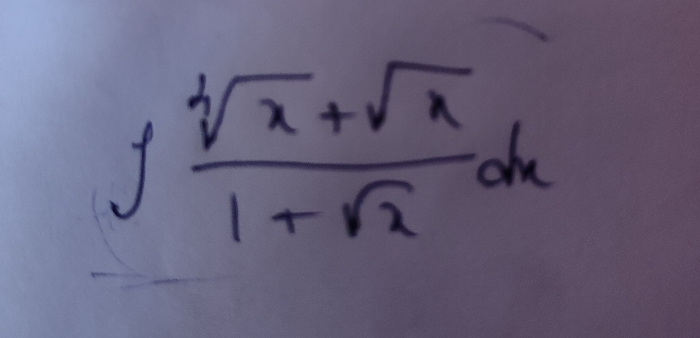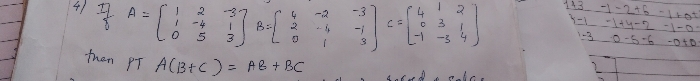CBSE Class 12-commerce Answered
Past records show that 80% of the operations performed by a certain doctor were successful . If he performs 4 operations per day what is the probability that at least 3 operations will be successful?
Please give the solution to the following question posted on 8th March : The projection of a vector on the coordinate axes are 6,-3, 2 resp. Find its length and direction cosines.
Also you had stated to give the answer to the second part of the second question posted on 8th March : Also find if the plane thus obtained
contains the line x-2/3=y-1/1= z-2/5 Pls tell if you have answered this part of the question.
Also pls refer your answer to my question posted on 3rd March : Find a unit vector in the XY plane which makes an angle of 45degree with vector i+j and 60 degree with the vector 3i-4j . You have stated in your answer that there is no such vector in the XY Plane.
However there is such a vector as per answer given in the book and the vector is 1/14(13i +j). Hence I request you to please check the answer provided by you . Thanks
Asked by ahuja8087 | 10 Mar, 2017, 12:26: AM
Dear student, the following are the solutions as we told you we shall provide. Hope this helps.

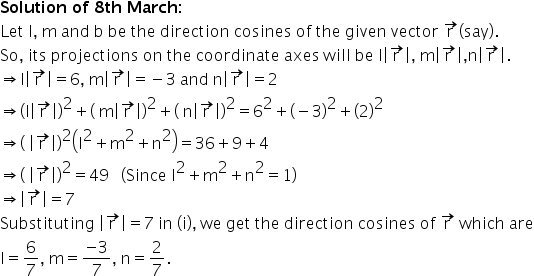 Answered by | 10 Mar, 2017, 05:29: PM
Answered by | 10 Mar, 2017, 05:29: PM
Application Videos
Concept Videos
CBSE 12-commerce - Maths
Asked by nainaadityathakur | 02 Apr, 2024, 12:56: PM
CBSE 12-commerce - Maths
Asked by nainaadityathakur | 17 Mar, 2024, 03:04: PM
CBSE 12-commerce - Maths
Asked by morninggood0966 | 29 Feb, 2024, 04:06: PM
CBSE 12-commerce - Maths
Asked by manishpaladiya652 | 28 Feb, 2024, 11:26: AM
CBSE 12-commerce - Maths
Asked by pathvipatel144 | 25 Feb, 2024, 09:37: PM
CBSE 12-commerce - Maths
Asked by nainaadityathakur | 06 Feb, 2024, 01:38: PM
CBSE 12-commerce - Maths
Asked by najakatkhan6698 | 25 Dec, 2023, 10:37: AM
CBSE 12-commerce - Maths
Asked by mounikachitrala342 | 26 Oct, 2023, 07:59: AM
CBSE 12-commerce - Maths
Asked by darshanasharma0409 | 21 Sep, 2023, 06:07: PM
CBSE 12-commerce - Maths
Asked by routdebasmita900 | 13 Aug, 2023, 10:43: AM