Class 9 LAKHMIR SINGH AND MANJIT KAUR Solutions Physics Chapter 1 - Motion
Motion Exercise 19
Solution 1
No, displacement is a vector quantity.
Solution 2
Distance is a scalar quantity.
Solution 3
6 m/s
= 6 x (3600/1000) km/hr = 21.6km/hr
Solution 4
Speed of a body in a specified direction is called velocity.
Solution 5
(a) Motion of a bus on a road
(b) Motion of a racing horse
Solution 6
Speed is defined as the distance travelled per unit time.
Solution 7
(a) The speedometer of a car measures instantaneous speed of the car.
(b) Odometer is a device used to record the distance travelled by the car.
Motion Exercise 20
Solution 8
Speed gives an idea of how slow or fast a body is moving.
Solution 9
When the body comes back to its starting point, it has zero resultant displacement but covers a certain non-zero distance.
Solution 10
In addition to speed, we should know the direction in which the body is moving.
Solution 11
When a body covers equal distances in equal intervals of time in a particular direction however small or big the time interval may be, the object is said to have uniform velocity.
Solution 12
When the object moves in a single straight line, the magnitude of average velocity equal to average speed.
Solution 13
Average velocity of a moving body can be zero.
Solution 14
Motion of a boy from his home to shop (in one direction) and back to home (in its reverse direction) is an example of a situation in which a body has a certain average speed but its average velocity is zero.
Solution 15
When a body is moving with uniform velocity, its acceleration is zero.
Solution 16
Negative acceleration is also called retardation.
Solution 17
(a) Speed (or Velocity)
(b) Acceleration
Solution 18
Uniformly accelerated motion
Solution 19
S.I. unit of retardation is m/s2.
Solution 20
(a) vector, scalar
(b) velocity
(c) acceleration, second, velocity, 3m/s
(d) displacement, m/s
(e) velocity, m/s2
Solution 21
A freely falling body has non-uniform motion because it covers smaller distances in the initial '1 second' intervals and larger distances in the later '1 second' intervals, i.e., it covers unequal distances in equal intervals of time.
Solution 22
Speed is a scalar quantity as it has magnitude only, it has no specified direction.
Solution 23
For bus X,
Speed= Distance/Time
Speed=360/5=72km/h
For bus Y,
Speed= Distance/Time
Speed=476/7=68 km/h
Speed of bus X is more than that of bus Y. Hence, bus X travels faster.
Solution 24
Speed of athelete = 10 m/s
Speed of bicycle = 200 m/min = 200/60 m/s = 3.33 m/s
Speed of scooter = 30 km/h = 30000/3600 m/s = 8.33 m/s
3.33 m/s < 8.33 m/s <10 m/s
i.e. 200 m/min < 30 km/h < 10 m/s
Solution 25
(a)Acceleration=![]()
![]()
(b) u = 0 m/s
v = 21 m/s
Time, t = 1 min = 60 sec

Solution 26
(a) Acceleration
(b) Retardation
(c) No, because if a body takes a round trip such that its final position is same as the starting position, then the displacement of the body is zero but the distance travelled is non-zero.
Solution 27
Average speed = Total distance travelled/ Total time taken
Total distance travelled = 100m = 0.1 km; Total time taken = 50 hr
Average speed= 0.1/50=0.002km/h
Motion Exercise 21
Solution 28
Total distance=100m =0.1 km
Total time taken=15 minutes= 15/60=0.25 hour
Average speed = Total distance travelled/ Total time taken
=0.1/0.25= 0.4km/h
Solution 29
Total distance travelled=100m
Total time taken = 9.83 sec
Average speed = Total distance travelled/ Total time taken
=100/9.83 =10.172m/s
Averge speed in km/h:
10.172 x(3600/1000)=36.62 km/h
Solution 30
Solution 31
Initial velocity= 0m/s
Final velocity=6m/s
Time=3 sec
Acceleration=![]()
=![]()
Solution 32
Initial velocity, u = 600 km/h
Final velocity, v = 1100 km/h
Acceleration = 10 km/h/s = 600 km/h2
From relation, a = (v-u)/t
t = (v-u)/a
t = (1100-600)/600 = 500/600 = 5/6 hr = 50 sec
Solution 33
Deceleration, a=-5m/s2
Initial velocity, u=20m/s
Final velocity, v=0m/s
t=?
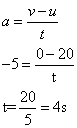
Solution 34
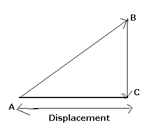
(a) Distance travelled is the actual length of the indirect path covered by the body whereas displacement refers to the straight line path between the initial and final positions. For e.g. In the figure given below, a body moves from point A to point B and then from point B to point C. Here, the distance travelled by the body is AB + BC and displacement is AC.
(b)
PQ=8cm
QR=6 cm
Resultant Displacement PR = ![]()
Solution 35
A body is said to be in motion when its position changes continuously with respect to a stationary object taken as reference point.
A body has uniform motion if it travels equal distances in equal intervals of time, no matter how small these time intervals may be. For example: a car running at a constant speed of 10m/s, will cover equal distance of 10m every second, so its motion will be uniform.
Non-uniform motion: A body has a non-uniform motion if it travels unequal distances in equal intervals of time. For example: dropping a ball from the roof of a tall building .
Solution 36
(a) Speed of a body is the distance travelled by it per unit time. The SI unit of speed is m/s.
(b) (i) Average speed of a body is the total distance travelled divided by the total time taken to cover this distance.
![]()
(ii) Uniform speed refers to the constant speed of a moving body. A body has a uniform speed if it travels equal distance in equal intervals of time, no matter how small these time intervals may be.
Solution 37
(a) Velocity of a body is the distance travelled by it per unit time in a given direction. SI unit of velocity is m/s.
( b) (i)Speed is a scalar quantity whereas velocity is a vector quantity.
(ii) Speed of a body is distance travelled by it per unit time whereas velocity of a body is the distance travelled by it per unit time in a given direction.
(iii)Speed is always positive whereas velocity can be both positive as well as negative.
(c) Speed = 54km/h = 54 x (1000/3600) = 15m/s
Solution 38
(a) Acceleration of a body is defined as the rate of change of its velocity with time. SI unit of acceleration is m/s2.
(b) A body has uniform acceleration if it travels in a straight line and its velocity increases by equal amounts in equal intervals of time. For example: Motion of a freely falling body.
Solution 39
Solution 40
Solution 41
Motion Exercise 22
Solution 55
Distance travelled in half a rotation of a circular path is equal to the circumference of semi-circle, i.e., =![]() R.
R.
Displacement= diameter of circle= 2R
Solution 56
(i) Distance travelled = 6 km
(ii) Displacement = zero (since final position is same as initial position)
Solution 57
(i) Total distance travelled= 3 + 4 +9=16 km
(ii) The body travels a total distance of 12 km in east direction i.e. towards x-axis.
And it travels a distance of 4 km in North direction, i.e. towards y-axis.
Hence, resultant displacement is
=![]()
Solution 58
(a) Total distance covered in going to the bookshop and coming back to the classroom = 20 + 20 = 40m
Total time taken= 25 + 25 = 50 sec
Solution 59
In the first case, car travels at a speed of 60 km/h for a distance of 100 km
In the second case, car travels at a speed of 40 km/h for a distance of 100 km
Total distance travelled = 200 km
Solution 60
Initial velocity, u=6m/s
Final velocity ,v=-4.4m/s (the ball rebounds in opposite direction)
Time, t = 0.040 s
Motion Exercise 39
Solution 3
The motion is accelerated.
Solution 4
It represents uniform velocity.
Solution 5
Distance travelled by the moving body .
Solution 6
The slope of a speed-time graph indicates acceleration.
Solution 7
The slope of a distance-time graph indicates speed.
Solution 8
Motion of moon around the earth.
Solution 9
Uniform circular motion.
Solution 10
The Speed of the body is constant or uniform.
Solution 2
Solution 1
(a) Speed
(b) Direction of motion
Motion Exercise 40
Solution 11
The body has uniform speed.
Solution 12
The body is not moving. It is stationary.
Solution 13
It represents non-uniform acceleration.
Solution 14
It is accelerated motion as the velocity is changing continuously.
Solution 15
The tip of the 'seconds' hand' of a watch represents uniform circular motion. It is an accelerated motion.
Solution 16
(a) zero
(b) speed
(c) acceleration
(d) distance travelled
(e) circular path
Motion Exercise 41
Solution 17
Yes, uniform circular motion is accelerated because the velocity changes due to continuous change in the direction of motion.
Solution 18
The speed of a body moving along a circular path is given by the formula:
![]()
where, v= speed
![]() =3.14 ( it is a constant)
=3.14 ( it is a constant)
t= time taken for one round of circular path
Solution 19
The motion of a body which is moving with constant speed in a circular path is said to be accelerated because its velocity changes continuously due to the continuous change in the direction of motion.
Solution 20
Uniform linear motion is uniform motion along a linear path or a straight line. The direction of motion is fixed. So, it is not accelerated. For e.g.: a car running with uniform speed of 10km/hr on a straight road.
Uniform circular motion is uniform motion along a circular path. The direction of motion changes continuously. So, it is accelerated. For e.g.: motion of earth around the sun.
Solution 21
An important characteristic of uniform circular motion is that the direction of motion in it changes continuously with time, so it is accelerated.
Centripetal force brings about uniform circular motion.
Solution 22
Initial velocity, u=?
Final velocity, v=0m/s (car is stopped)
Retardation, a=-2.5 m/s2
Time, t=10s
v=u + at
0=u +(-2.5)x 10
u=25m/s
Solution 23
The velocity of this body is increasing at a rate of '10 metres per second' every second.
Initial velocity, u=0m/s
Time, t=2s
Acceleration, a=10m/s2
Using , ![]()
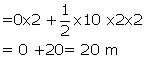
Solution 24
Initial velocity, u=5m/s
Final velocity, v=?
Acceleration, a=0.2m/s2
Time, t=10 sec
Using , v=u + at
v=5 + 0.2 x 10
v=5 + 2 =7 m/s
Now distance travelled in time is calculated;
Using, ![]()
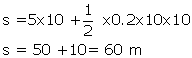
Solution 25
Initial velocity, u=18km/h
Final velocity, v=0m/s
Time, t=2.5 sec
Acceleration, a=?
Using , v= u + at
![]()
So, retardation is 2m/s2.
Solution 26
Initial velocity, u=0m/s
Final velocity, v=?
Acceleration, a=0.2 m/s2
Time, t=5min= 5 x60=300 sec
Using, v = u + at
v =0 + 0.2 x 300=60m/s
And the distance travelled is
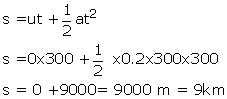
Solution 27
(a) Distance and Time
(b) Speed (or velocity) and Time
Solution 28
Initial velocity, u=0m/s
Final velocity, v=?
Acceleration, a=2m/s2
Time, t=10s
(a) Using, v = u + at
v=0 + 2 x 10= 20 m/s
(b) Distance travelled is:

Solution 29
Initial velocity, u=20m/s
Time, t=30 s
Acceleration, a=0.5m/s2
Distance travelled is:

Solution 30
Initial velocity, u=15m/s
Final velocity, v=0m/s
Distance, s=18m
Acceleration, a=?
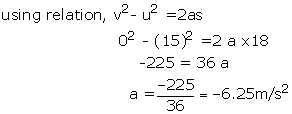
So, deceleration is 6.25 m/s2.
Solution 31
Solution 32
(a) The train has a uniform velocity.
(b) There is no acceleration.
Solution 33
(a) v=u + at is the first equation of motion. It gives the velocity acquired by a body in time t when the body has initial velocity u and uniform acceleration a.
(b) Initial velocity, u=0m/s
Time, t=5 s
Distance, s=100m
Acceleration, a=?
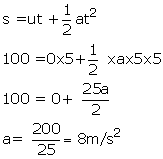
Solution 34
(a) Consider a body having initial velocity 'u'. Suppose it is subjected to a uniform acceleration 'a' so that after time't' its final velocity becomes 'v'. Now, from the definition of acceleration we know that:

(b) Initial velocity, u=54km/h= 15m/s
Final velocity, v=0m/s
Time, t=8s
Acceleration, a=?
![]()
Solution 35
(a) Suppose a body has an initial velocity 'u' and a uniform acceleration' a' for time 't' so that its final velocity becomes 'v'. Let the distance travelled by the body in this time be 's'. The distance travelled by a moving body in time 't' can be found out by considering its average velocity. Since the initial velocity of the body is 'u' and its final velocity is 'v', the average velocity is given by:
(b) Initial velocity, u=0m/s
Final velocity, v=36km/h=10m/s
Time, t=10min =10 x 60=600 sec
Acceleration, a=?

Solution 36
Solution 37
(a) When a body moves in a circular path with uniform speed (constant speed), its motion is called uniform circular motion. For e.g.
(i) Artificial satellites move in uniform circular motion around the earth.
(ii) Motion of a cyclist on a circular track.
(b) The speed of a body moving along a circular path is given by the formula:
![]()
Given, t=60 sec
Radius, r=10.5cm=0.105 m
![]()
Motion Exercise 42
Solution 38
Consider the velocity-time graph of a body shown in figure.
The body has an initial velocity u at a point A and then its velocity changes at a uniform rate from A to B in time t. In other words, there is a uniform acceleration a from A to B, and after time t its final velocity becomes v which is equal to BC in the graph. The time t is represented by OC. To complete the figure, we draw the perpendicular CB from point C, and draw AD parallel to OC. BE is the perpendicular from point B to OE.
Now, Initial velocity of the body, u= OA -----(1)
And, Final velocity of the body, v=BC ------(2)
But from the graph BC =BD + DC
Therefore, v=BD + DC ------(3)
Again DC = OA
So, v =BD + OA
Now, from equation (1), OA =u
So, v=BD + u ------(4)
We should find out the value of BD now. We know the slope of a velocity-time graph is equal to the acceleration, a.
Thus, Acceleration, a= slope of line AB
or a = BD/AD
But AD =OC= t, so putting t in place of AD in the above relation, we get:
![]()
or BD=at
Now, putting this value of BD in equation(4), we get:
v= u+ at
Solution 39
Consider the velocity-time graph of a body shown in figure. The body has an initial velocity u at a point A and then its velocity changes at a uniform rate from A to B in time t. In other words, there is a uniform acceleration a from A to B, and after time t its final velocity becomes v which is equal to BC in the graph. The time t is represented by OC.
Suppose the body travels a distance s in time t. In the figure, the distance travelled by the body is given by the area of the space between the velocity-time graph AB and the time axis OC, which is equal to the area of the figure OABC. Thus:
Distance travelled = Area of figure OABC
= Area of rectangle OADC + area of triangle ABD
Now, we will find out the area of rectangle OADC and area of triangle ABD.
(i) Area of rectangle OADC =OA x OC
= u x t
=ut
(ii) Area of triangle ABD= (1/2)x Area of rectangle AEBD
=(1/2) x AD x BD
=(1/2) x t x at
=(1/2)at2
Distance travelled, s = Area of rectangle OADC + area of triangle ABD
![]()
Solution 40
Consider the velocity-time graph of a body shown in figure. The body has an initial velocity u at a point A and then its velocity changes at a uniform rate from A to B in time t. In other words, there is a uniform acceleration a from A to B, and after time t its final velocity becomes v which is equal to BC in the graph. The time t is represented by OC. To complete the figure, we draw the perpendicular CB from point C, and draw AD parallel to OC. BE is the perpendicular from point B to OE.
The distance travelled s by a body in time t is given by the area of the figure OABC which is a trapezium.
Distance travelled, s= Area of trapezium OABC

Now, OA + CB = u + v and OC =t Putting these values in the above relation, we get:
![]()
Eliminate t from the above equation. This can be done by obtaining the value of t from the first equation of motion.
Thus, v = u + at (first equation of motion)
And, at = v
Motion Exercise 43
Solution 53
(i) The distance covered from A to B is ( 3-0) =3 cm
Time taken to cover the distance from A to B =(5 -2) =3s
![]()
![]()
(ii) The speed of the body as it moves from B to C is zero.
(iii) The distance covered from C to D is (7-3)=4 cm
Time taken to cover the distance from C to D = (9-7)=2s
![]()
Solution 54
(a) The body has a uniform velocity if its displacement-time graph is a straight line.
(b) The body has a uniform acceleration if its velocity-time graph is a straight line.
Solution 55
Solution 56
(i) BC represents uniform velocity. From graph, we see that the velocity of the body at point C = 40km/h
(ii) Acceleration between A and B = slope of line AB
=![]()
(iii) BC represents uniform velocity, so acceleration acting on the body between B and C is zero.
Solution 57
Distance travelled = Area of rectangle OABC
= OA x OC
= 5 x 5 =25 m
Solution 58
Solution 59
Solution 60
(i) Initial speed of the car=10km/h
(ii) Maximum speed attained by the car= 35km/h
(iii) BC represents zero acceleration.
(iv) CD represents varying retardation.
(v)
Solution 61
(i) Graph (c): The speedof the ball goes on decreasing uniformly as it moves upward, reaches zero at the highest point, and then increases uniformly as it moves downward.
(ii) Grap(a): The speed of the trolley decreases uniformly, then it moves at a constant speed, and then the speed increases uniformly.
Motion Exercise 44
Solution 62
(i) OA represents uniform acceleration
(ii) AB represents constant speed.
(iii) BC represents uniform retardation.
(iv) Acceleration of car from O to A = slope of line OA
(v) Acceleration of car from A to B is zero as it has uniform speed during this time.
(vi) Retardation of car from B to C = slope of line BC
Solution 63
(i) Graph (a) represents uniform acceleration.
(ii) Graph (b) represents constant speed.
(iii) Graph (c) represents uniform retardation.
(iv) Graph (d) represents non-uniform retardation.
Solution 64
Initial velocity, u=8m/s
Acceleration, a=1m/s2
Distance, s=18m
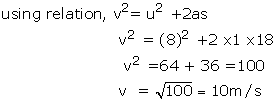
Solution 65
Initial velocity, u=20m/s
Final velocity, v=0m/s
Distance, s=50m
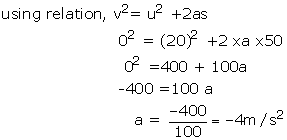
The car's deceleration must be 4 m/s2.

