Class 9 LAKHMIR SINGH AND MANJIT KAUR Solutions Physics Chapter 3 - Gravitation
Gravitation Exercise 100
Solution 1
Value of gravitational constant G on the earth and the moon is = 6.67 x 10-11Nm2/kg2
Note that the value of G always remains constant irrespective of the location.
Solution 2
Gravitational force is responsible for the moon revolving round the earth.
Solution 3
No, the acceleration produced in a freely falling body is independent of the mass of the body.
Solution 4
Johannes Kepler gave the three laws of planetary motion.
Solution 5
Newton explained the motion of planets on the basis of gravitational force between the sun and planets.
Solution 6
Kepler's law of periods states that: The cube of the mean distance of a planet from the sun is directly proportional to the square of time it takes to move around the sun.
Solution 7
Kepler's third law of planetary motion led Newton to establish the inverse-square rule for gravitational force between two bodies.
Solution 8
Extremely large mass of the earth.
Solution 9
Acceleration produced in a freely falling body, irrespective of its mass, is 9.8m/s2
Solution 10
Gravitational force of the earth.
Solution 11
The gravitational force F between two bodies of masses M and m kept at a distance d from each other is :
![]()
Here, Gravitational constant, G=6.7 x10-11Nm2 kg-2
Solution 12
Gravitational force is responsible for the earth revolving round the sun.
Solution 13
Gravitational force causes two objects lying apart attract each other.
Solution 14
Gravitational force (exerted mainly by the moon and to some extent by the sun) is involved in the formation of tides in the sea.
Solution 15
Gravitational force of the sun holds the solar system together.
Solution 16
Weight, W = m x g
= 1 kg x 9.8m/s2=9.8 N
Solution 17
The weight of a body is directly proportional to its mass.
It also depends on the acceleration due to gravity which varies from place to place.
Solution 18
Weight of the body varies with altitude; mass of an object is constant.
Solution 19
Its weight varies; mass of an object is constant.
Solution 20
Weight, W=m x g
= 10 x 9.8 =98 N
Solution 21
Weight, W=m x g
![]()
Solution 22
Its weight will be zero as value of g is zero at the centre of the earth.
Solution 23
Weight, W=m x g
=50 x 9.8=490N
Solution 24
Weight of the body on the surface of moon will be 1N approx. as the value of g on the surface of moon is one-sixth that of the earth.
Solution 25
(a) True
(b) False
(c) False
(d) False
(e) False
Gravitation Exercise 101
Solution 26
(a) One-sixth
(b) Mass
(c) Six times
(d) One-sixth
(e) Six times
(f) 36N
Solution 27
This is the acceleration produced by the earth. It is also called acceleration due to gravity.
![]()
where, G= gravitational constant
M= mass of the earth.
R=radius of the earth
Solution 28
(a)The falling of a body from a height towards the Earth under the gravitational force of the Earth (with no other forces acting on it) is called free fall.
(b)No, acceleration is independent of the mass of the body during free fall.
Solution 29
Yes, Newton's third law of motion holds good for the force of gravitation. This means that when earth exerts a force of attraction on an object, then the object also exerts an equal force on the earth, in the opposite direction.
Solution 30
The force of gravitation between two bodies is directly proportional to the product of their masses.
![]()
Since the mass of cricket balls is very small as compared to that of the earth, so the force of gravitation between two cricket balls is extremely small while that between a ball and the earth is extremely large.
Solution 31
The gravitational force F between two bodies of masses M and m kept at a distance d from each other is :
![]()
The force between two bodies is inversely proportional to the square of the distance between them. That is,
![]()
Therefore , if we double the distance between two bodies, the gravitational force becomes one-fourth and if we halve the distance between two bodies, then the gravitational force becomes four times.
Solution 32
(a) If we double the distance between two bodies, the gravitational force becomes one-fourth.
(b) If we halve the distance between two bodies, then the gravitational force becomes four times.
Solution 33
(i) Universal law of gravitation is used to determine the masses of the sun, the earth and the moon accurately.
(ii) Universal law of gravitation helps in discovering new stars and planets.
Solution 34
This is because the earth exerts a force of attraction (called gravity) on the stone and pulls it down.
Solution 35
![]()
m=50kg
M=120kg
Distance, d=10m
G=6.7 x 10-11 Nm2/kg2
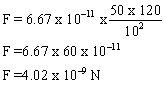
Solution 36
Force due to gravity, ![]()
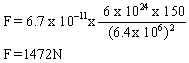
Solution 37
Distance d=1.5 x 108 km= 1.5 x 1011 m
Mass of the sun, m=2 x1030 kg
Mass of the earth, M= 6 x 1024kg
Force of gravitation, ![]()
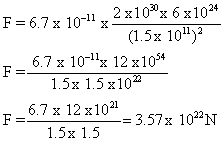
Solution 38
Initial velocity of the stone, u=?
Final velocity of stone, v=0
Acceleration due to gravity, g= -9.8m/s2
Time, t=3 sec
Using relation, v=u + gt
0 = u -9.8 x 3
u =29.4m/s
Solution 39
Initial velocity, u=0m/s
Acceleration due to gravity, g=9.8m/s2
Time taken to reach the ground, t=2.5 sec
Height, h=?
Using relation,

Solution 40
Height, s=20m
Initial velocity, u=0
Acceleration due to gravity, g=10m/s2
Final velocity, v=?
Time taken, t=?
(i) Using relation,
(ii) For a freely falling body:
v2 = u2 + 2gh
= (0)2 + 2 x (10) x (20)
So, v2 =400
![]()
Solution 41
Initial velocity, u=20m/s
Final velocity, v=0
Acceleration due to gravity, g=-9.8m/s2
Height, h=?
Using relation, for a freely falling body:
v2 = u2 + 2gh
(0)2 = (20)2 + 2 x (-9.8) x h
0-400 = -19.6 h
h= 400/19.6 = 20.4 m
Solution 42
Initial velocity, u=?
Final velocity, v=0
Acceleration due to gravity, g=-10m/s2
Height, h=5 m
(a) For a freely falling body:
v2 = u2 + 2gh
(0)2 = u2+ 2 x(-10)x 5
0= u2 -100
u2= 100
So, u=10m/s
(b) Using relation, v=u + gt
0 = 10 + (-10) t
-10= -10 t
t=1sec
Solution 43
|
Mass |
Weight |
|
1. The mass of an object is the quantity of matter contained in it. |
1. The weight of an object is the force with which it is attracted towards the centre of the earth. |
|
2. SI unit of mass is kilogram (kg). |
2. SI unit of mass is newton (N). |
|
3. The mass of an object is constant. |
3. The weight of an object is not constant. It changes with the change in acceleration due to gravity. |
|
4. The mass of an object can never be zero. |
4. The weight of an object can be zero. |
Solution 44
Yes, weight of a body is not constant, it varies with the value of acceleration due to gravity, g.
Weight of a body is zero, when it is taken to the centre of the earth or in the interplanetary space, where g=0.
Gravitation Exercise 102
Solution 45
Weight= 9.8N
W= m x g
9.8 =m x 9.8
m= 1kg
Force, F= mass x acceleration
20 N = 1kg x a
Acceleration, a=20m/s2
Solution 46
Weight, W= m x g
20=m x 10
m=2 kg
Solution 47
(i) Its mass will be 20 kg as mass is a constant quantity.
(ii) Weight, W= m x g
=20 x 1.6=32 N
Solution 48
The mass of a body is more fundamental because mass of a body is constant and does not change from place to place.
Solution 49
The weight of an object on the moon is about one-sixth of its weight on the earth. This is because the value of acceleration due to gravity on the moon is about one-sixth of that on the earth.
Solution 50
(a) The mass of a body is the quantity of matter contained in it. The SI unit of mass is kilogram (kg).
(b) The weight of a body is the force with which it is attracted towards the centre of the earth. The SI unit of weight is newton (N).
(c) Weight, W =m x g, i.e. the weight of a body is directly proportional to its mass.
Solution 51
(a) According to universal law of gravitation: Every body in the universe attracts every other body with a force (F) which is directly proportional to the product of their masses (m and M) and inversely proportional to the square of the distance (d) between them.
![]()
Sir Isaac Newton gave this law.
(b) The gravitational constant G is numerically equal to the force of gravitation which exists between two bodies of unit masses kept at a unit distance from each other.
![]()
Units of gravitational constant= Nm2/kg2
Solution 52
(a) The uniform acceleration produced in a freely falling body due to the gravitational force of the earth is called acceleration due to gravity of earth.
(b) Usual value of acceleration due to gravity, g=9.8 m/s2.
(c) SI unit of acceleration due to gravity is m/s2.
Solution 53
(a) No, the value of acceleration due to gravity (g) is not constant at all the places on the surface of the earth. Since the radius of the earth is minimum at the poles and maximum at the equator, the value of g is maximum at the poles and minimum at the equator. As we go up from the surface of the earth, the distance from the centre of the earth increases and hence the value of g decreases. The value of g also decreases as we go down inside the earth.
(b) Acceleration due to gravity,
![]()
Mass, M= 7.4 x 1022kg
Radius, R =1.74 x 106m
Gravitational constant, G= 6.7 x 10-11Nm2/kg2

As the value of g =1.637m/s2, which is one sixth the value of g on earth, the satellite could be moon.
Solution 54
Kepler's first law: The planets move in elliptical orbits around the sun, with the sun at one of the two foci of the elliptical orbit. This law means that the orbit of a planet around the sun is an ellipse and not an exact circle. An elliptical path has two foci, and the sun is at one of the two foci of the elliptical path.
Kepler's Second law states that: Each planet revolves around the sun in such a way that the line joining the planet to the sun sweeps over equal areas in equal intervals of time. This means that a planet does not move with constant speed around the sun. The speed is greater when the planet is nearer the sun, and less when the planet is farther away from the sun.
Kepler's Third Law states that: The cube of the mean distance of a planet from the sun is directly proportional to the square of time it takes to move around the sun.
![]()
Solution 55
Acceleration due to gravity,
![]()
Mass, M = 6x 1024kg
Diameter = 12.8 x 103 km = 12.8 x 106 m
Radius, R = (12.8 x 106)/2 =6.4x 106m
Gravitational constant, G= 6.7 x 10-11Nm2/kg2
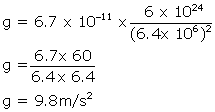
As the value of g=9.8m/s2, the planet could be Earth.
Gravitation Exercise 103
Solution 71
Gravitational force is given by:
![]()
Distance between two masses is increased s.t. new distance is D= 5 d
New gravitational force F1 = F
Let on of the mass is changed to m1 so as to maintain the same gravitational force.
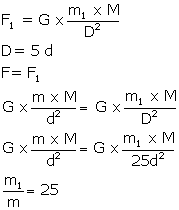
m1 = 25m
Hence one of the masses should be increased by 25 times in order to have the same gravitational force.
Solution 72
In order to be able to notice the gravitational force of attraction between any two objects, at least one of the objects on the earth should have an extremely large mass. Since no object on the earth have an extremely large mass, we cannot notice such forces.
The two objects in a room do not move towards each other because due to their small masses, the gravitational force of attraction between them is very, very weak.
Solution 73
Acceleration due to gravity of earth,
![]()
If mass of planet, m= M/2
And radius of planet, r= R/2
Acceleration due to gravity on the surface of planet will be:
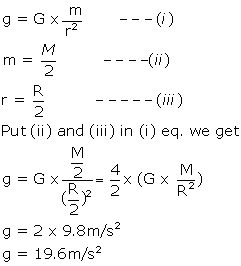
Gravitation Exercise 104
Solution 74
The coin reaches the ground first as compared to the piece of paper because it experiences lesser resistance from air than that felt by paper.
If the coin and the piece of paper are dropped in vacuum, both of them will touch the ground at the same time.
Solution 75
The mass of a stone is very small, due to which the gravitational force produces a large acceleration in it. Due to large acceleration of stone, we see stone falling towards the earth. The mass of earth is, however, very, very large. Due to the very large mass of the earth, the same gravitational force produces very, very small acceleration in the earth, that it cannot be observed. And hence we do not see the earth rising up towards the stone.
Solution 76
The actual shape of the orbit of a planet around the sun is elliptical.
The assumption made by the Newton regarding the shape of an orbit of a planet around the sun was that the orbit of a planet around the sun is 'circular'.
Solution 77
(a) 9.23 m/s2 , 7.34 m/s2 , 3.08 m/s2 , 1.49 m/s2 , 0.57 m/s2 , 0.30 m/s2
(b) This distance F of 10000 km is high up in the sky. The distance of 10000 km cannot be deep inside the earth because the radius of earth is only about 6400km and the value of g at the centre of earth becomes zero.
Gravitation Exercise 123
Solution 1
Grams per cubic centimtre (g/cm3).
Solution 2
Density of water =1000kg/m3.
Solution 3
Relative density of water is 1.
Solution 4
Pressure has unit of Pascal (Pa).
Solution 6
(a) False
(b) True
Solution 7
Buoyant force on an object due to a liquid acts in the vertically upward direction.
Solution 8
Upthrust is the other name of buoyant force.
Solution 9
Buoyant force.
Solution 10
The upward force acting on an object immersed in a liquid is called upthrust.
Solution 11
Archimedes' Principle.
Solution 12
The relative density of mercury is 13.6, this means that mercury is 13.6 times as heavy as an equal volume of water.
Solution 13
Pressure is 'thrust per unit area'.
Solution 14
Buoyant force or upthrust.
Solution 15
The tendency of a liquid to exert an upward force on an object placed in it, is called buoyancy.
Solution 16
The buoyant force on a boat is caused by the pressure of water 'pushing up' on the bottom of the boat.
Solution 17
The density of ice is less than that of water, so ice floats in water.
Solution 18
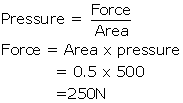
Solution 19
Since the object floats in the liquid, so the magnitude of the buoyant force exerted by the liquid is equal to the weight of the object.
Hence, buoyant force =200N
Solution 20
Archimedes gave the magnitude of buoyant force acting on a solid object immersed in a liquid
Solution 21

Solution 22
Volume=5m3
Density= 3000kg/m3
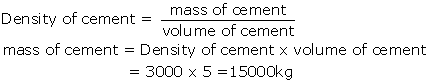
Solution 23
Mass of the substance = 100g
Volume of the substance =10cm3

Solution 24
Solution 25
The body will float when dipped in a bucket of water as its density is less than that of water.
Solution 26
(a) pressure
(b) buoyant
(c) average
(d) all; increases
(e) less; density
(f) weight; area
(g) bigger; smaller
Solution 5
Gravitation Exercise 124
Solution 27
(a) The density of a substance is defined as mass of the substance per unit volume.
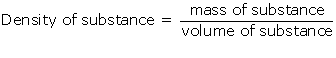
SI unit of density is kg/m3.
The relative density of a substance is the ratio of its density to that of water.

It has no units.
(b)

Solution 28
The force acting on a body perpendicular to its surface is called thrust.
The SI unit of thrust is newton (N).
Solution 29
A mug full of water appears light as long as it is under water because buoyant force acts on it which reduces its effective weight and makes it appear lighter.
Solution 30
As more and more volume of the solid object is immersed in the liquid, the upward 'buoyant force' also keeps on increasing. When the object is completely immersed in the liquid, the buoyant force acting on the solid becomes maximum and remains constant thereafter.
Solution 31
As more and more volume of our body is immersed in water, the apparent weight of the body goes on decreasing and the body seems to become lighter. This is due to the increase in upward buoyant force acting on the body.
Solution 32
Big boulders weig much less while in water and as such are easily moved by the flood.
Solution 33
An iron nail sinks in water but it floats in mercury because density of iron is more than that of water but less than that of mercury.
Solution 34
A piece of glass sinks in water but it floats in mercury because density of glass is more than that of water but less than that of mercury.
Solution 35
A piece of steel sinks in water because steel is denser than water. However, a steel ship is a hollow object made of steel and contains a lot of air in it. Due to presence of a lot of air in it, the average density of the ship becomes less than the density of water. Hence a ship floats in water.
Solution 36
School bags have wide straps so that their weight may spread over a large area of shoulder producing less pressure on the shoulder.
Solution 37
A sharp knife cuts objects easily because due to its very thin edge, the force of our hand falls on a very small area of the object producing large pressure.
Solution 38
Concrete or wooden sleepers are kept below the railway line so that the weight of passing train is spread over a large area of ground and the track may not sink into the ground.
Solution 39
A wide steel belt is provided over the wheels of an army tank so that they exert less pressure on the ground and do not sink into it.
Solution 40
The tip of the sewing needle is sharp so that due to its sharp tip, the needle may put the force on a very small area of the cloth, producing a large pressure sufficient to pierce the cloth being stitched.
Solution 41
When a man is walking, then at one time only one foot is on the ground. Due to this, the force of weight of man falls on a smaller area of the ground and produces more pressure on the ground. On the other hand, when the man is standing, then both his feet are on the ground. Due to this, the weight of the man falls on a larger area of the ground and produces lesser pressure on the ground.
Solution 42
Snow shoes stop us from sinking into soft snow because due to large area of snow shoes, our weight is spread over a large area of the snow producing small pressure.
Solution 43
When a person stands on a cushion then only his two feet (having small area) are in contact with the cushion. Due to this the weight of man falls on a small area of the cushion producing a large pressure causing a big depression in the cushion. On the other hand, when the same person lies down on the cushion, then his whole body (having large area) is in contact with the cushion. Here, his weight falls on a much larger area of the cushion producing much smaller pressure and very little depression in the cushion.
Solution 44
Flat shoes have greater area in contact with the soft sand as compared to heels. Due to this, there is less pressure on soft sand because of which they do not sink much in the sand and it is easy to walk on it.
Solution 45
A nail has a pointed tip, so that when it is hammered, the force of hammer is transferred to a very small area of wood creating a large pressure which pushes the nail into the wood.
Gravitation Exercise 125
Solution 46
The foundations of buildings and dams are laid on a large area of ground so that the weight of the building or dam produces less pressure on the ground and they may not sink into the ground.
Solution 47
On the other hand, a piece of iron is denser than water, so it sinks in water.
Solution 48
Camels have large flat feet so that there is a greater area in contact with the sand which produces less pressure on the sand and the camels can move easily on the sand.
Solution 49
(a) Buoyant force
(b) Force of friction
(c) Gravitational force
(d) Reaction force
Solution 50
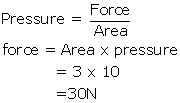
If the area is made one-third i.e. 1m2, then the force would be:
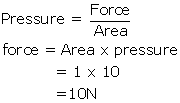
Solution 51
Force, F= 550N
Area of contact of one shoe =160 cm2 =160 x 10-4m2
Area of contact with two shoes =160 x 2 =320 cm2=320 x 10-4m2
(a) If the girl stands on two feet,
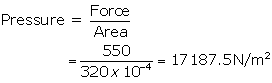
(b)
If she stands on one foot,
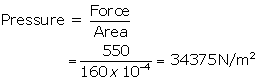
Solution 52
Volume =3m3
Mass = 9kg
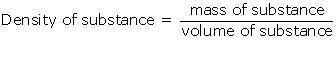
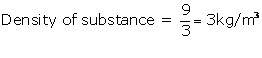
And density of water = 1000kg/m3
The object will float in the water as the density of the object is less than the density of water.
Solution 53
The object will weigh less in water because an upward force (buoyant force) equal to the weight of water displaced acts on the object when immersed in water which reduces its weight apparently.
Solution 54
(a)

(b)
For material A:
Mass= 5kg
Volume =20 cm3 = 20 x 10-6m3
For material B:
Mass =20kg
Volume =90 cm3 = 90x 10-6m3
Density of material A is more than density of material B.
Solution 55
(a) The upward force acting on an object immersed in a liquid is called buoyant force.
Factors affecting buoyant force:
(i) Volume of object immersed in the liquid,
(ii) Density of the liquid.
(b) The cause of buoyant force is the greater upward pressure exerted by water underneath the object..
(c) Mass of water displaced = 600kg
Weight of water displaced, W =m x g
=600 x 10 =6000N
Since, the weight of water displaced by the boat is 6000N, therefore the buoyant force acting on the boat will also be 6000N.
Solution 56
(a) According to the principle of floatation: An object will float in a liquid if the weight of object is equal to the weight of liquid displaced by it.
Weight of object = Weight of liquid displaced by it.
(b) Weight of water displaced by boat= 6000N
(i) Buoyant force =6000N, as the weight of water displaced is equal to buoyant force.
(ii) Weight of a floating object = Weight of water displaced by it = 6000N
Solution 57
(a) The density of a substance is defined as mass of the substance per unit volume.
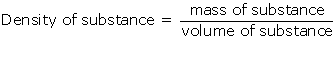
SI unit of density is kg/m3.
(b) Relative density of a substance is the ratio of its density to that of water.
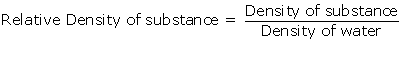
Relative density has no units as it is a ratio of two similar quantities.
(c) Density of turpentine =840kg/m3
Density of water=1000kg/m3

Solution 58
(a) Pressure is the force acting perpendicularly on a unit area of the object.
(b)
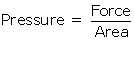
(c) (i) Pressure on an area of 10 m2
Force =200N

(ii) Pressure on an area of 5 m2
Force =200N

Gravitation Exercise 126
Solution 59
(a) Those substances which can flow easily are called fluids. All the liquid and gases are fluids, like water, air etc.
(b) Archimedes' Principle :
When an object is wholly (or partially) immersed in a liquid, it experiences a buoyant force (or upthrust) which is equal to the weight of liquid displaced by the object.
Buoyant force on an object = weight of liquid displaced by that object
(c) If the buoyant force exerted by the liquid is less than the weight of the object, the object will sink in the liquid. If the buoyant force exerted by the liquid is equal to or greater than the weight of the object, the object will float in the liquid.
Solution 60
(a) A floating boat displaces water equal to its own weight. This displaced water exerts buoyant force to balance the weight of boat and keep it afloat.
(b) (i) Mass = 96 g
Volume = 12cm3
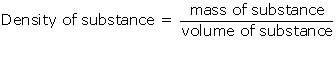
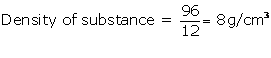
(ii) Mass = 96 x 10-3kg
Volume =12 x 10-6m3
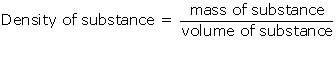
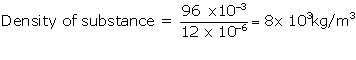
Solution 61
Weight of elephant=40000N
Area of one foot =1000 cm2= 1000 x 10-4m2
Weight of girl=400N
Area of heel of girl =1 cm2=1 x 10-4m2
(a) Elephant has a larger weight of 40000N, therefore, elephant exerts a larger force on the ground. Elephant exerts a larger force on the ground by 40000N - 400 N=39600N.
(b) Weight of elephant = 40000N
Area of one foot =1000cm2= 1000 x 10-4m2

(c) Weight of the girl = 400N
Area of heel of girl = 1 cm2 = 1 x 10-4m2

(d) Girl exerts a larger pressure on the ground.
(e)
The pressure exerted by girl is 10 times greater than that exerted by the elephant.
Gravitation Exercise 127
Solution 72
The two equal weights of unequal volumes which are balanced in air, will get imbalanced when they are completely dipped in water because due to their unequal volumes, they will displace unequal volumes of water and hence suffer unequal loss in weight.
Solution 73
No, it is not necessary that their weights in air should also be the same. This is because the two bodies have undergone the same loss in weight on completely immersing in water due to their equal volumes and not because of their equal weights, so they may have different weights in air.
Solution 74
The body will sink less in water. This is because the density of water is more than that of kerosene due to which water will exert a greater upward buoyant force on the body.
Solution 75
The reading on spring balance will be zero. This is because the weight of floating block of wood is fully supported by the liquid in which it is floating and hence it does not exert any force on the spring balance.
Solution 76
When a lot of salt is dissolved in water, then the density of salt solution becomes much more than pure water. Due to its much higher density, the salt solution exerts a greater upward buoyant force on the egg making it rise and then float.
Gravitation Exercise 128
Solution 77
(a) The reading of spring balance will not change if a cork is placed in water because cork, being lighter than water, floats in water.
(b) The reading of spring balance will change if a piece of heavy metal is placed in water because heavy metal being denser than water, sinks in water.
Solution 78
Volume of golf ball = rise in water level = 30 cm3
Solution 79
(a) The boat sinks a little more in water, that is, the boat floats lower in water.
(b) The weight of water displaced (by the submerged part of the boat) increases.
(c) The buoyant force acting on the boat increases.
Solution 80
The sheet of tin sinks in water because the density of tin is higher than that of water. When the same sheet of tin is converted into a box or a boat, then due to the trapping of lot of 'light' air in the box or boat, the average density of the box or boat made of tin sheet becomes lower than that of water and hence it floats in water.

