Question Paper (Section wise)
-
1) A mixture of 2 moles of helium gas (atomic mass = 4 u), and 1 mole of argon gas (atomic mass = 40 u) is kept at 300 K in a container. The ratio of their rms speeds
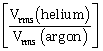 , is close to:
, is close to:-
3.16
-
0.32
-
0.45
-
2.24
-
-
2) A current loop, having two circular arcs joined by two radial lines is shown in the figure. It carries a current of 10 A. The magnetic field at point O will be close to:
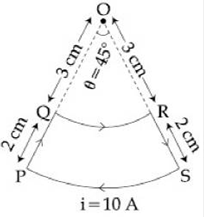
-
1.0 × 10-7 T
-
1.5 × 10-7 T
-
1.5 × 10-5 T
-
1.0 × 10-5 T
-
-
3) Three charges +Q, q, +Q are placed respectively, at distance 0, d/2 and d from the origin, on the x-axis. If the net force experienced by +Q, placed at x = 0, is zero, then value of q is
-
-Q/4
-
+Q/2
-
+Q/4
-
-Q/2
-
-
4) An unknown metal of mass 192 g heated to a temperature of 100°C was immersed into a brass calorimeter of mass 128 g containing 240 g of water at a temperature of 8.4°C. Calculated the specific heat of the unknown metal if water temperature stabilized at 21.5°C. (Specific heat of brass is 394 J kg-1k-1).
-
458 J kg-1K-1
-
919 J/Kg K-1
-
Th = 1.5Tc
-
Th = 0.5c
-
-
5) The self-produce emf of a coil is 25 volts. When the current in it is changed at uniform rate from 10 A to 25 A in 1 s, the change in the energy of the inductance is:
-
740 J
-
437.5 J
-
540 J
-
637.5 J
-
-
6) A parallel plate capacitor having capacitance 12 pF is charged by a battery to a potential difference of 10 V between its plates. The charging battery is now disconnected and a porcelain slab of dielectric constant 6.5 is slipped between the plates. The work done by the capacitor on the slab is:
-
692 pJ
-
508 pJ
-
560 pJ
-
600 pJ
-
-
7) A hydrogen atom, initially in the ground state is excited by absorbing a photon of wavelength 980 Å. The radius of the atom in the excited state, in terms of Bohr radius a0, will be (hc = 12500 eV-Å)
-
25a0
-
9a0
-
16a0
-
4a0
-
-
8) A particle undergoing simple harmonic motion has time dependent displacement given by
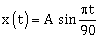 . The ratio of kinetic to potential energy of the particle at t = 210s will be
. The ratio of kinetic to potential energy of the particle at t = 210s will be-
1/9
-
1
-
2
-
1/3
-
-
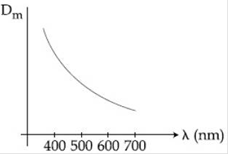
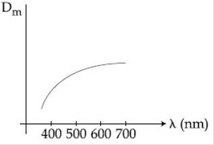
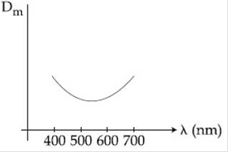
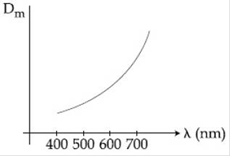
9) The variation of refractive index of a crown glass thin prism with wavelength of the incident light is shown. Which of the following, graph is the correct one, if Dm is the angle of minimum deviation?
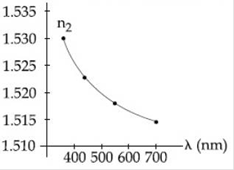
-
-
10) A plano-convex lens (focal length f2, refractive index µ2, radius of curvature R) fits exactly into a plano- concave lens (focal length f1, refractive index µ1, radius of curvature R). Their plane surfaces are parallel to each other. Then, the focal length of the combination will be:
-
f1 – f2
-
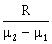
-

-
f1 + f2
-
-
11) A vertical closed cylinder is separated into two parts by a frictionless piston of mass m and of negligible thickness. The piston is free to move along the length of the cylinder. The length of the cylinder above the piston is l1, and that below the piston is l2, such that l1 > l2. Each part of the cylinder contains n moles of an ideal gas at equal temperature. T.
(R is universal gas constant and g is the acceleration due to gravity)
-
-
12) In a Frank-hertz experiment, an electron of energy 5.6 eV passes through mercury vapour and emerges with an energy 0.7 eV. The minimum wavelength of photons emitted by mercury atoms is close to:
-
1700 nm
-
2020 nm
-
220 nm
-
250 nm
-
-
13) A convex lens (of focal length 20 cm) and a concave mirror, having their principal axes along the same lines, are kept 80 cm apart from each other. The concave mirror is to the right of the convex lens. When an object is kept at a distance of 30 cm to the left of the convex lens, its image remains at same position even if the concave mirror, by itself would produce a virtual image would be:
-
20 cm
-
10 cm
-
30 cm
-
20 cm
-
-
14) A particle starts from origin O from rest and moves with a uniform acceleration along the positive x – axis. Identify all figures that correctly represent the motion qualitatively. (a = acceleration, v = velocity, x = displacement, t = time)
a.
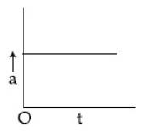
b.
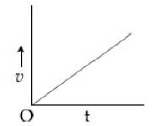
c.
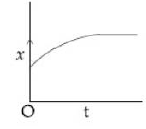
d.
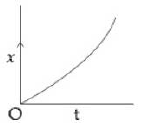
-
a, b, c
-
A
-
b, c
-
a, b, d
-
-
15) The given diagram shows four processes i.e., isochoric, isothermal and adiabatic. The correct assignment of the processes, in the same order is given by:

-
a d c d
-
a d b c
-
d a c b
-
d a b c
-
-
16) An NPN transistor is used in common emitter configuration as an amplifier with 1 kΩ load resistance. Signal voltage of 10 mV is applied across the base-emitter. This produces a 3 mA change in the collector current and 15 μA change in the base current of the amplifier. The input resistance and voltage gain are:
-
0.67 kΩ, 300
-
0.67 kΩ, 200
-
0.33 kΩ, 1.5
-
0.33 kΩ, 300
-
-
17) Following figure shows two processes A and B for a gas. If ∆QA and ∆QB are the amount of heat absorbed by the system in two cases, and ∆UA and ∆UB are changes in internal energies, respectively, then:

-
∆QA = ∆QB; ∆UA = ∆UB
-
∆QA > ∆QB; ∆UA = ∆UB
-
∆QA < ∆QB; ∆UA < ∆UB
-
∆QA > ∆QB; ∆UA > ∆UB
-
-
18) A stationary horizontal disc is free to rotate about its axis. When a torque is applied on it, its kinetic energy as a function of θ, where θ is the angle by which it has rotated, is given as kθ2. If its moment of inertia is I then the angular acceleration of the disc is:
-
-
19) A bullet of mass 20 g has an initial speed of 1 ms-1 just before it starts penetrating a mud wall of thickness 20 cm. If the wall offers mean resistance of 2.5 × 10-2 N, the speed of the bullet after emerging from the other side of the wall is close to
-
0.7 ms-1
-
0.3 ms-1
-
0.1 ms-1
-
0.4 ms-1
-
-
20) In free space, a particle A of charge 1 µ C is held fixed at a point P. Another particle B of the same charge and mass 4 µg is kept at a distance of 1 mm from P. If B is released, then its velocity at a distance of 9 mm from P is

-
1.5 × 102 m/s
-
2.0 × 103 m/s
-
1.0 m/s
-
None
-
-
21) A source of sound S is moving with the velocity of 50 m/s towards a stationary observer. The observer measures the frequency of the sound as 1000Hz. The apparent frequency of the source when it is moving away from the observer after crossing him is ______.
(Take velocity of sound in air is 350 m/s)
-
22) What will be value of x in the given equation below which is used to express dimension of resistance?
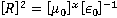
(Here, R is electrical resistance, ∈0 is the permittivity of vacuum and μ0 is the permeability of vacuum)
-
23) Unpolarized light of intensity I passes through an ideal polarizer A. Another identical polarizer B is placed behind A. The intensity of light beyond B is found to be
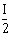 . Now another identical polarizer C is placed between A and B. The intensity beyond B is now found to be
. Now another identical polarizer C is placed between A and B. The intensity beyond B is now found to be . The angle between polarizer A and C is ________°.
. The angle between polarizer A and C is ________°. -
24) A spaceship orbits around a planet at a height of 20 km from surface. Assuming that only gravitational field of the plant acts on the spaceship. The approximate number of revolution made by the spaceship in 24 hours around the plane is ______.
[Given: Mass of plane = 8 × 1022 kg, Radius of planet = 2 × 106 m, Gravitational constant G = 6.67 × 10-11 Nm2/kg2]
-
25) A plane is inclined at an angle α = 30° with respect to the horizontal. A particle is projected with a speed u = 2 ms-1, from the base of the plant, making an angle θ = 15° with respect to the plane as shown in the figure. The distance from the base at which the particle hits the plane is close to ______ cm.
(Take, g = 10 m/s2)
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) 0.5 moles of gas A and X moles of gas B exert a pressure of 200 Pa in a container of volume 10m3 at 1000 K. Given R is the gas constant in JK-1 moI-1,x is
-
-
2) A solution of sodium sulphate contains 92 g of Na+ ions per kilogram of water. The Molality of Na+ ions in that solution in mol kg-1 is
-
12
-
4
-
8
-
16
-
-
3) According to molecular orbital theory, which of the following is true with respect to
 and
and 
-
 is unstable and
is unstable and 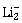 is stable
is stable -
 is stable and
is stable and 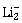 is unstable
is unstable -
Both are stable
-
Both are unstable
-
-
4) Among the following reactions of hydrogen with halogens, the one that requires a catalyst is:
-
H2 + l2 → 2HI
-
H2 + CI2 → 2HCI
-
H2 + Br2 → 2HBr
-
H2 + F2 → 2HF
-
-
5) The process with negative entropy change is:
-
Dissociation of CaSo4(s) to CaO(s) and SO3(g)
-
Sublimation of dry ice
-
Dissolution of iodine in water
-
Synthesis of ammonia from N2 and H2
-
-
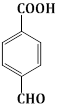
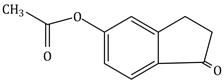
6) The major product obtained in the following reaction is:
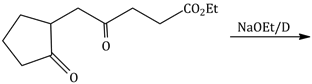
-
-
7) A 10 g effervescent tablet containing sodium bicarbonate and oxalic acid releases 0.25 ml of CO2 at T = 298.15 K and p = 1 bar. If molar volume of CO2 is 25.0 L under such condition, what is the percentage of sodium bicarbonate in each tablet? [Molar mass of NaHCO3= 84 g mol-1]
-
0.84
-
33.6
-
16.8
-
8.4
-
-
8) An organic compound is estimated through Dumas method and was found to evolve 6 mole of CO2, 4 moles of H2O and 1 mole of nitrogen gas. The formula of the compound is:
-
C12H8N
-
C12H8N2
-
C6H8N2
-
C6H8N
-
-
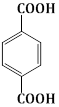
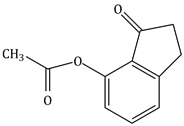
9) The major product of the following reaction is
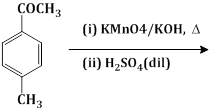
-
-
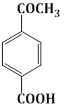
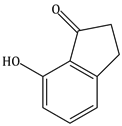
10) The major product of the following reaction is:
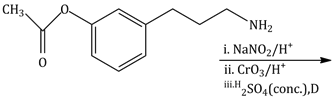
-
-
11) An open vessel at 27°C is heated until two fifth of the air (assumed as an ideal gas) in it has escaped from the vessel. Assuming that the volume of the vessel remains constant, the temperature at which the vessel has been heated is:
-
500°C
-
500 K
-
750°C
-
750 K
-
-
12) The upper stratosphere consisting of the ozone layer protects us from the sun’s radiation that falls in the wavelength region of:
-
200 – 315 nm
-
400 – 550 nm
-
0.8 – 1.5 nm
-
600 – 750 nm
-
-
13) Calculate the standard cell potential (in V) of the cell in which following reaction takes place:
Fe2 + (aq) + Ag+ (aq) →Fe3+(aq)+ Ag (s)
Given that:
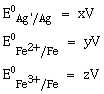
-
x – z
-
x + y –z
-
x – y
-
x + 2y – 3z
-
-
14) The covalent alkaline earth metal halide
(X = Cl, Br, l)is:
-
BeX2
-
CaX2
-
SrX2
-
MgX2
-
-
15) Which one of the following alkenes when treated with HCl yields majorly an anti Markovnikov product?
-
H2N –CH = CH2
-
F3C –CH = CH2
-
CH3O – CH = CH2
-
Cl – CH = CH2
-
-
16) Consider the van der Waals constants, a and b, for the following gases.
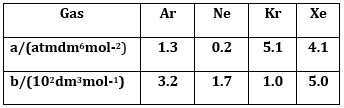
Which gas is expected to have the highest critical temperature?
-
Ar
-
Xe
-
Kr
-
Ne
-
-
17) Among the following the set of parameters that represents path functions, is:
a. q + w
b. q
c. w
d. H – TS
-
(b) and (c)
-
(b), (c) and (d)
-
(a), (b) and (c)
-
(a) and (d)
-
-
18) The degenerate orbitals of [Cr(H2O)6]3+ are:
-
dxz and dyz
-
dx2-y2 and dxy
-
dyz and dz2
-
dz2 and dxz
-
-
19) The difference between ΔH and ΔU (ΔH - ΔU), when the combustion of one mole of heptane (I) is carried out a temperature T is equal to
-
-4 RT
-
-3 RT
-
3 RT
-
4 RT
-
-
20) The correct order of the first ionization enthalpies is
-
Mn < Ti < Zn < Ni
-
Zn < Ni < Mn < Ti
-
Ti < Mn < Zn < Ni
-
Ti < Mn < Ni < Zn
-
-
21) How many statement/s is/are INCORRECT for Rf in chromatography?
- Rf value depends on the type of chromatography
- The value of Rfcannot be more than one.
- Higher Rfvalue means higher adsorption.
- Rfvalue is dependent on the mobile phase.
-
22) How many products will formed in the following reaction?
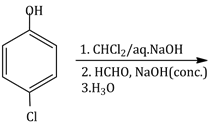
-
23) Among the following how many number of species are responsible for photochemical smog?
CO2, NO, NO2, O3, SO2, N2 and hydrocarbons
-
24) The atomic number of a metal with ‘Zn’ symbol gives hydrogen gas upon treatment with both acid as well as base is:
-
25) Consider the following reaction and statements:
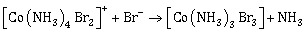
- Two isomers are produced if the reactant complex ion is a cis-isomer
- Two isomers are produced if the reactant complex ion is a trans-isomer
- Only one isomer is produced if the reactant complex ion is a trans-isomer
- Only one isomer is produced if the reactant complex ion is a cis-isomer
The correct statements are
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) If y = y(x) is a solution of the differential equation
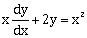 satisfying y(1) = 1, then y
satisfying y(1) = 1, then y 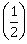 is equal to:
is equal to: -
-
2) For x ϵ R – {0, 1}, let f1(x) =
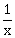 , f2(x) = 1 – x and f3(x) =
, f2(x) = 1 – x and f3(x) = 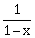 be three given functions. If a function, J(x) satisfies (f2oJof1) (x) = f3(x) then J(x) is equal to:
be three given functions. If a function, J(x) satisfies (f2oJof1) (x) = f3(x) then J(x) is equal to:-
f3(x)
-
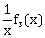
-
f2(x)
-
f1(x)
-
-
3) Let
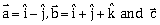 be a vector such that
be a vector such that 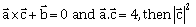 is equal to:
is equal to:-
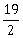
-
9
-
8
-
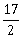
-
-
4) The value of λ such that sum of the squares of the roots of a quadratic equation x2 + (3 – λ) x + 2 = λ, has the least value is:
-
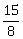
-
1
-
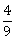
-
2
-
-
5) Let f: (-1, 1) → R be a function defined by f(x) = max
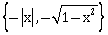 . If K be the set of all points at which f is not differentiable, then K has exactly:
. If K be the set of all points at which f is not differentiable, then K has exactly:-
five elements
-
one elements
-
three elements
-
two elements
-
-
6) The number of values of θ ϵ (0, π) for which the system of linear equations, x + 3y + 7z = 0, -x + 4y + 7z = 0 and (sin3θ) x + (cos2θ) y+ 2z = 0 has a non-trivial solution, is:
-
Three
-
Two
-
Four
-
One
-
-
7) 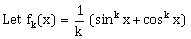 for k = 1, 2, 3,… Then for all x ϵ R, the value of f4(x) – f6(x) is equal to:
for k = 1, 2, 3,… Then for all x ϵ R, the value of f4(x) – f6(x) is equal to: -
-
8) The area (in sq. units) of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is:
-
5/4
-
9/8
-
7/8
-
3/4
-
-
9) The value of r for which 20Cr 20C0 + 20Cr-1 20C1 + 20Cr-2 20C2 + … + 20C0 20Cr is maximum is:
-
15
-
20
-
11
-
10
-
-
10) In a game, a man wins Rs. 100 if he gets 5 or 6 on a throw of a fair die and loses Rs. 50 for getting any other number on the die. If he decides to throw the die either till he gets a five or a six or to a maximum of three throws, then his expected gain/loss (in rupees) is:
-
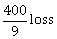
-
0
-
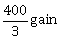
-

-
-
11) If a straight line passing through the point P(-3, 4) is such that its intercepted portion between the coordinate axes is bisected at P, then its equation is:
-
3x – 4y + 25 = 0
-
4x – 3y + 24 = 0
-
x – y + 7 = 0
-
4x + 3y = 0
-
-
12) Let z1 and z2 be two complex numbers satisfying
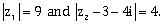 Then the minimum value of
Then the minimum value of 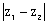 is:
is:-
0
-
√2
-
1
-
2
-
-
13) Which one of the following statements is not a tautology?
-
(p ˅ q) → (p ˅ (∼q))
-
(p ˅ q) → p
-
p → (p ˅ q)
-
(p ˄ q) → (∼p) ˅ q
-
-
14) If a point R(4, y, z) lies on the line segment joining the points P(2, –3, 4) and Q(8, 0, 10), then the distance of R from the origin is:
-
√53
-
6
-
2√14
-
2√21
-
-
15) If the fourth term in the binomial expansion of
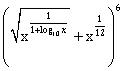 is equal to 200, and x > 1, then the value of x is:
is equal to 200, and x > 1, then the value of x is:-
104
-
100
-
103
-
10
-
-
16) If the standard deviation of the numbers -1, 0, 1, k is √5 where k > 0, then k is equal to:
-
-
17) If f(x) is a non-zero polynomial of degree four, having local extreme points at x = -1, 0, 1; then the set S = {x ϵ R; f(x) = f(0)} contains exactly:
-
four irrational numbers
-
four rational numbers
-
two irrational and one rational number
-
two irrational and two rational numbers
-
-
18) Let the sum of the first n terms of a non-constant A.P., a1, a2, a3, ……… be
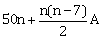 , where A is a constant. If d is the common difference of this A.P., then the ordered pair (d, a50) is equal to:
, where A is a constant. If d is the common difference of this A.P., then the ordered pair (d, a50) is equal to:-
(A, 50 + 46A)
-
(A, 50 + 45A)
-
(50, 50 + 45A)
-
(50, 50 + 46A)
-
-
19) If the line ax + y = c, touches both the curves x2 + y2 = 1 and y2 = 4√2x then |c| is equal to:
-

-
√2
-
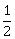
-
2
-
-
20) If the plane 2x – y + 2z + 3 = 0 has the distances
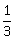 and
and 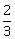 units from the planes 4x – 2y + 4z + λ = 0 and 2x – y + 2z + µ = 0, respectively, then the maximum value of λ + µ is equal to:
units from the planes 4x – 2y + 4z + λ = 0 and 2x – y + 2z + µ = 0, respectively, then the maximum value of λ + µ is equal to: -
15
-
13
-
5
-
9
-
-
21) If
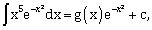 where c is a constant of integration, then g(–2) is equal to _________.
where c is a constant of integration, then g(–2) is equal to _________. -
22) If ey + xy = e such that the ordered pair
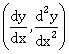 at x = 0 is equal to
at x = 0 is equal to 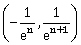 , then the value of n is _____.
, then the value of n is _____. -
23) If the equation y = sin x sin(x + 2) – sin2(x + 1) represents a straight line, then the number of quadrants it lies in is ___________.
-
24) For x ∊ R, let [x] denote the greatest integer ≥ x, then the sum of the series
 is equal to ________.
is equal to ________. -
25) If
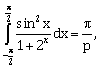 the value of p is _______.
the value of p is _______.
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25