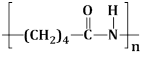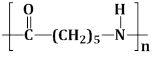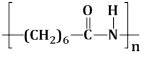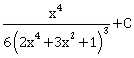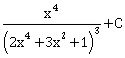Question Paper (Section wise)
-
1) For a uniformly charged ring of radius R, the electric field on its axis has the largest magnitude at a distance h from its center. Then value of is:
-

-
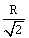
-
R
-
R√2
-
-
2) Two coherent source produce waves of different intensities which interfere. After interference, the ratio of the maximum intensity to the minimum intensity is 16. The intensity of the waves are in the ratio:
-
16 : 9
-
25 : 9
-
4 : 1
-
5 : 3
-
-
3) Temperature difference of 120°C is maintained between two ends of a uniform rod AB of length 2L. Another bent rod PQ, of same cross-section as AB and length
 , is connected across AB (see figure). In steady state, temperature difference between P and Q will be closed to:
, is connected across AB (see figure). In steady state, temperature difference between P and Q will be closed to:
-
45°C
-
75°C
-
60°C
-
35°C
-
-
4) Two vectors
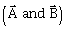 have equal magnitudes. The magnitude of
have equal magnitudes. The magnitude of  is ‘n‘ times the magnitude of
is ‘n‘ times the magnitude of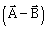 . The angle between
. The angle between 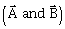 is:
is: -
-
5) The eye can be regarded as a single refracting surface. The radius of curvature of this surface is equal to that of cornea (7.8 mm). This surface separates two media of refractive indices 1 and 1.34. Calculated the distance from the refracting surface at which a parallel beam of light will come to focus.
-
1 cm
-
2 cm
-
4.0 cm
-
3.1 cm
-
-
6) A closed organ pipe has a fundamental frequency of 1.5 kHz. The number of overtones that can be distinctly heard by a person with this organ pipe will be: (Assume that the highest frequency a person can hear is 20,000 Hz).
-
6
-
4
-
7
-
5
-
-
7) The equilateral triangle ABC is cut from a thin solid sheet of wood. (See figure) D, E and F are the mid points of its sides as shown and G is the centre of the triangle. The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane of the triangle is I0. If the smaller triangle DEF is removed from ABC, the moment of inertia of the remaining figure about the same axis is I. Then:
-
-
8) Ice at –20° C is added to 50 g of water at 40° C. When the temperature of the mixture reaches 0° C, it is found that 20 g of ice is still unmelted. The amount of ice added to the water was close to (Specific heat of water = 4.2 J/g/°C) Heat of fusion of water at 0°C = 334 J/g)
-
50g
-
100g
-
60g
-
40g
-
-
9) A gas mixture consists of 3 moles of oxygen and 5 moles or argon at temperature T. Considering only translational and rotational modes, the total internal energy of the system is:
-
15 RT
-
12 RT
-
4 RT
-
20 RT
-
-
10) In the figure, given that VBB supply can vary from 0 to 5.0 VCC = 5 V, βdc = 200, RB = 100 kΩ, Rc =1kΩ an VBE = 1.0 V, The minimum base current and the input voltage at which the transistor will go to saturation, will be respectively:
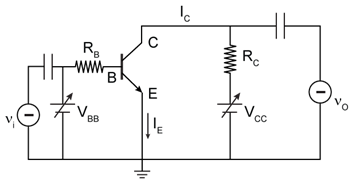
-
25 µA and 3.5 V
-
20 µA and 3.5 V
-
25 µA and 2.8 V
-
20 µA and 2.8 V
-
-
11) A long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is 5 cm and its rotational speed is 2 rotations per second, then the difference in the heights between the centre and the sides, in cm, will be:
-
2.0
-
0.1
-
0.4
-
1.2
-
-
12) A particle of mass 20 g is released with an initial velocity 5 m/s along the curve from the point A, as shown in the figure. The point A is at height h from point B. The particle slides along the frictionless surface. When the particle reaches point B, its angular momentum about O will be: [Take g = 10 m/s2]

-
2 kg-m2/s
-
8 kg-m2/s
-
6 kg-m2/s
-
3 kg-m2/s
-
-
13) A damped harmonic oscillator has a frequency of 5 oscillations per seconds. The amplitude drops to half its value for every 10 oscillations. The time it will take to drop to
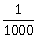 of the original amplitude is closed to:
of the original amplitude is closed to:-
10 s
-
100 s
-
50 s
-
20 s
-
-
14) The temperature, at which the root mean square velocity of hydrogen molecules equals their escape velocity form the earth is closest to:
[Boltzman’s Constant kB = 1.38 × 10-23 J/k
Avogadro number N˄ = 6.02 × 1026 / kg
Radius of Earth: 6.4 × 106 m
Gravitation acceleration on Earth = 10 ms2]
-
800k
-
104 K
-
3 × 105
-
650 K
-
-
15) In the figure shown, what is the current (in Ampere) drawn from the battery? You are given R1 = 15Ω, R2 = 10 Ω, R3 = 20Ω, R4 = 5Ω, R5 = 25Ω, R6 = 30Ω, E = 15V
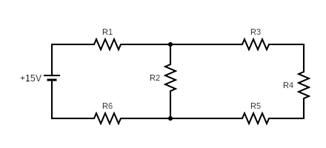
-
13/24
-
7/18
-
9/32
-
20/3
-
-
16) A uniform cable of mass ‘M’ and length ‘L’ is placed on a horizontal surface such that its
 part is hanging below the edge of the surface. To lift the hanging part of the cable up to the surface, the work done should be:
part is hanging below the edge of the surface. To lift the hanging part of the cable up to the surface, the work done should be:-
nMgL
-
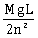
-
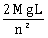
-
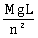
-
-
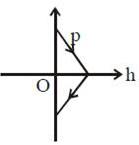
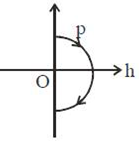
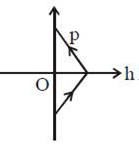
17) A ball is thrown vertically up (taken as + z-axis) from the ground. The correct momentum height (p-h) diagram is:
-
-
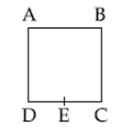
18) A wire of resistance R is bent to form a square ABCD as shown in the figure. The effective resistance between E and C is: (E is mid-point of arm CD)
-

-

-
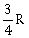
-
R
-
-
19) A solid sphere of mass M and radius R is divided into two unequal parts. The first part has a mass of
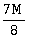 and is converted into a uniform disc of radius 2R. The second part is converted into a uniform solid sphere. Let l1 be the moment of inertia of the disc about its axis and l2 be the moment of inertia of the new sphere about its axis. The ratio of l1/l2 is given by:
and is converted into a uniform disc of radius 2R. The second part is converted into a uniform solid sphere. Let l1 be the moment of inertia of the disc about its axis and l2 be the moment of inertia of the new sphere about its axis. The ratio of l1/l2 is given by:-
285
-
185
-
65
-
140
-
-
20) A metal coin of mass 5 g and radius 1 cm is fixed to a thin stick AB of negligible mass as shown in the figure. The system is initially at rest. The constant torque, that will make the system rotate about AB at 25 rotation per second is 5 s is close to

-
2.0 × 10-5 Nm
-
4.0 × 10-6 Nm
-
1.6 × 10-5 Nm
-
7.9 × 10-6 Nm
-
-
21) The figure shows a square loop L of side 5 cm which is connected to a network of resistances. The whole set up is moving towards right with a constant speed of 1 cms-1 At some instant, a part of L is in a uniform magnetic field of 1 T, perpendicular to the plane of the loop. If the resistance of L is 1.7 Ω, the current in the loop at that instant will be close to _____ μA.
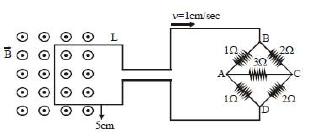
-
22) A magnetic compass needle oscillates 30 times per minute at a place where the dip is 45°, and 40 times per minute where the dip is 30°. If B1 and B2 are respectively the total magnetic field due to the earth at the two places, then the approximate value of B1 is _____ T, when B2 is 50 T.
-
23) The trajectory of a projectile near the surface of the earth is given as y =x – 9x2. For the given case the angle of projection with respect to ground is _____ °.
-
24) A load of mass M kg is suspended from a steel wire of length 2 m and radius 1.0 mm in Searle’s apparatus experiment. The increase in length produced in the wire is 4.0 mm. Now the load is fully immersed in a liquid of relative density 2. The relative density of the material of load is 8. The new value of increase in length of the steel wire is ______ mm.
-
25) An alpha-particle of mass m suffers 1-deminisional elastic collision with a nucleus at rest of unknown mass. It is scattered directly backwards losing, 64% of its initial kinetic energy. The mass of the nucleus is ______×m.
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
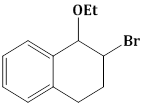
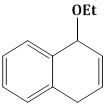
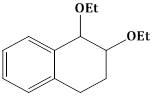
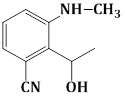
1) The major product of the following reaction is:

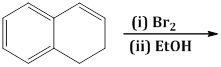
-
-
2) A water sample has ppm level concentration of the following metal:
Fe = 0.2, Mn = 5.0, Cu = 3.0, Zn = 5.0. The metal that makes the water sample unsuitable for drinking is.
-
Cu
-
Mn
-
Fe
-
Zn
-
-
3) The increasing order of pKa of following amino acids in aqueous solution is Gly, Asp, Lys, Arg
-
Asp < Gly < Arg < Lsy
-
Gly < Asp < Arg < Lsy
-
Asp < Gly < Lys < Arg
-
Arg < Lys < Gly < Asp
-
-
4) In the cell Pt(s) H2(g,1bar)|HCl(aq)|AgCl(s)|Ag(s)|Pt(s) the cell potential is 0.92V when a 10–6 molal HCl solution is used. The standard electrode potential of (AgCl/Ag,Cl- )
elctrode is :
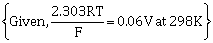
-
0.94 V
-
0.76 V
-
0.40 V
-
0.20 V
-
-
5) For an elementary chemical reaction,
the expression for
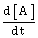 is
is-
k1[A2] – k-1[A]2
-
2k1[A2] - k-1[A]2
-
k1[A2] + k-1[A]2
-
2k1[A2] - 2k-1[A]2
-
-
6) A compound of formula A2B3 has the hcp lattice. Which atom forms the hcp lattice and what fraction of tetrahedral voids is occupied by the other atoms:
-
-
7) Which compounds out of the following is/are not aromatic?




-
b, c and d
-
c and d
-
B
-
a and c
-
-
8) An example of solid sol is:
-
Paint
-
Gem stones
-
Butter
-
Hair cream
-
-
9) Match the metal column I with the coordination compounds/enzymes column II
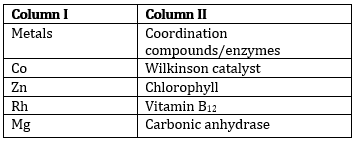
-
a – iii, b – iv, c – i, d - ii
-
a – i, b – ii, c- iii, d - iv
-
a – ii, b – i, c – iv, d - iii
-
a – iv, b – iii, c – i, d - ii
-
-
10) The magnetic moment of an octahedral homoleptic Mn(II) complex is 5.9 BM. The suitable ligand for this complex is:
-
ethylenediamine
-
CN-
-
NCS-
-
CO
-
-
11) The correct statement(s) among I to III with respect to potassium ions that are abundant within the cell fluids is/are:
- They activate many enzymes.
- They participate in the oxidation of glucose to produce ATP.
- Along with sodium ions, they are responsible for the transmission of nerve signals.
-
I and II only
-
I and III only
-
I, II and III
-
III only
-
12) For a certain reaction consider the plot of 𝓁nk versus 1/T given in the figure. If the rate constant of this reaction at 400 K is 10–5 s–1, then the rate constant at 500 K is:
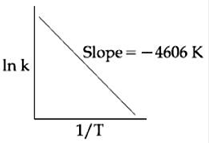
-
10-6 s-1
-
2 × 10-4s-1
-
10-4s-1
-
4 ×10-4s-1
-
-
13) The structure of Nylon – 6 is:
-
-
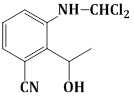
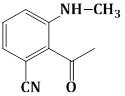
14) The major product obtained in the following reactions is”
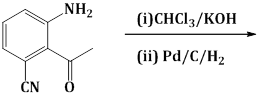
-
-
15) Consider the bcc unit cells of the solid 1 and 2 with the position of atoms as shown below. The radius of atom B is twice of atom A. The unit cell edge length is 50% more in solid 2 than in 1. What is the approximate packing efficency in solid 2?

-
90%
-
75%
-
65%
-
45%
-
-
16) The aerosol is a kind of colloid in which:
-
Solid is dispersed in gas
-
gas is dispersed in solid
-
liquid is dispersed in water
-
gas in dispersed in liquid
-
-
17) The given plots represents the variation of the concentration of a reactant R with time for two different reactions (i) and (ii). The respective orders of the reactions are:


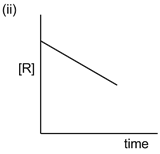
-
1, 1
-
0, 2
-
0, 1
-
1, 0
-
-
18) Aniline dissolved in dilute HCl is reacted with sodium nitrite at 0° C. This solution was added drop wise to a solution containing equimolar mixture of aniline and phenol in dil. HCl. The structure of the major products is:
-
-
19) The ratio of the shortest wavelength of two spectral series of hydrogen spectrum is found to be about 9. The spectral series are:
-
Lyman and Paschen
-
Brackett and Pfund
-
Paschen and Pfund
-
Balmer and Brackett
-
-
20) For the reaction,
2SO2(g) + O2(g) → 2SO3(g)
∆H= -57.2 kJ mol-1 and
KC=1.7×1016
Which of the following statement is INCORRECT?
-
The equilibrium constant is large suggestive of reaction going to completion and so no catalyst is required.
-
The equilibrium will shift in forward direction as the pressure increase.
-
The equilibrium constant decreases as the temperature increases.
-
The addition of inert gas at constant volume will not affect the equilibrium constant.
-
-
21) The pH of a 0.02 M NH4Cl solution will be
[given Kb (NH4OH) = 10–5 and log 2 = 0.301]
-
22) In how many regions electrons are more likely to be found?
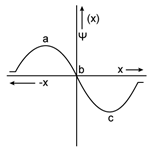
-
23) 5 moles of AB2 weigh 125 × 10-3 kg and 10 moles A2B2 weigh 300 × 10-3 kg. The molar mass of A(MA) and molar mass of B(MB) in g mol-1 are:
-
24) An element has a face-centred cubic (fcc) structure with a cell edge of a. The distance between the centres of two nearest tetrahedral voids in the lattice is: a ⨯ ______.
-
25) Number of chiral Monochlorinated product/s obtained on chlorination of 2-methylbutane is ______ .
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) If a, b and c be three distinct numbers in G.P. and a + b + c = xb then x cannot be
-
-2
-
-3
-
4
-
2
-
-
2) If
 then x is equal to:
then x is equal to: -
-
3) The system of linear equation x + y + z = 2, 2x + 3y + 2z = 5, 2x + 3y + (a2 - 1) z = a + 1 then it…
-
is inconsistent when a = 4
-
has a unique solution for |a| = √3
-
has infinitely many solutions for a = 4
-
is inconsistent when |a| = √3
-
-
4) Let
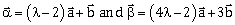 be two given vectors where
be two given vectors where 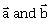 are non collinear. The value of λ for which vectors
are non collinear. The value of λ for which vectors 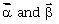 are collinear, is:
are collinear, is:-
-4
-
-3
-
4
-
3
-
-
5) If the probability of hitting a target by a shooter, in any shot, is
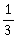 then the minimum number of independent shots at the target required by him so that the probability of hitting the target at least once is greater than
then the minimum number of independent shots at the target required by him so that the probability of hitting the target at least once is greater than  is
is-
3
-
6
-
5
-
4
-
-
6) The plane which bisects the line segment joining the points (–3, –3, 4) and (3, 7, 6) at right angles, passes through which one of the following points?
-
(-2, 3, 5)
-
(4, -1, 7)
-
(2, 1, 3)
-
(4, 1, -2)
-
-
7) If tangents are drawn to the ellipse x2 +2y2 = 2 at all points on the ellipse other than its four vertices, then the mid points of the tangents intercepted between the coordinate axes lie on the curve:
-
-
8) If x loge (loge x) – x2 + y2 = 4 (y > 0), then
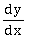 at x = e is equal to:
at x = e is equal to: -
-
9) Let f: R → R be defined by f (x) =
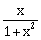 , x ϵ R. Then the range of f is:
, x ϵ R. Then the range of f is:-

-
R – [-1, 1
-
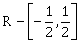
-
(-1, 1) – {0}
-
-
10) The integral
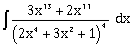 is equal to (where C is a constant of integration)
is equal to (where C is a constant of integration) -
-
11) The tangent to the curve y = x2 - 5x + 5, parallel to line 2y = 4x + 1, also passes through the point:
-
-
12) The total number of irrational terms in the binominal expansion of (71/5 – 31/10)60 is
-
55
-
49
-
48
-
54
-
-
13) If
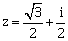 , then (1+iz+z5 +iz8)9 is equal to:
, then (1+iz+z5 +iz8)9 is equal to:-
-1
-
1
-
(-1+2i) 9
-
0
-
-
14) The number of four – digit numbers strictly greater than 4321 that can be formed using the digits 0, 1, 2, 3, 4, 5 (repetition of digits is allowed) is:
-
360
-
288
-
310
-
306
-
-
15) The tangent and the normal lines at the point (√3, 1) to the circle x2+ y2= 4 and the x – axis form a triangle. The area of this triangle (in square units) is:
-
-
16) For any two statements p and q, the negation of the expression p ˅ (∼ p ˄ q ) is:
-
p ⟷ q
-
∼ p ˅ ∼q
-
∼ p ˄ ∼q
-
p ˄ q
-
-
17) If a tangent to the circle x2 + y2 = 1 intersects the coordinate axes at distinct points P and Q, then the locus of the mid- point of PQ is:
-
x2 + y2 – 16x2y2 = 0
-
x2 + y2 – 2x2y2 = 0
-
x2 + y2 – 4x2y2 = 0
-
x2 + y2 – 2xy = 0
-
-
18) If the function f defined on
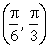 by
by f (x) =

is continuous, then k is equal to:
-
1
-
2
-
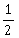
-
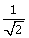
-
-
19) The sum of real roots of the equation
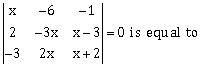
-
-4
-
0
-
6
-
1
-
-
20) The angles A, B and C of triangle ABC are in A. P. and a: b = 1:√3. If c = 4 cm, then the area (in sq. cm) of this triangle is
-
2√3
-
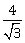
-
4√3
-
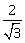
-
-
21) Let y = y (x) be the solution of the differential equation
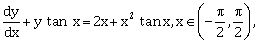 such that y (0) = 1. Then
such that y (0) = 1. Then -
22) Let f: R → R be a continuously differentiable function such that f (2) = 6 and f '(2) =
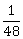 . If
. If 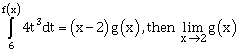 is equal to:
is equal to: -
23) If the data x1, x2, ...., x10 is such that the mean of first four of these is 11, the mean of the remaining six is 16 and the sum of squares of all of these is 2,000; then the standard deviation of this data is :
-
24) Let Sn denote the sum of the first n terms of an A.P. If S4 = 16 and S6 = –48, then S10 is equal to:
-
25) 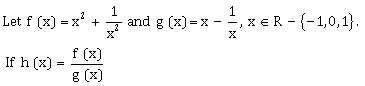 , then the local minimum value of h(x) is:
, then the local minimum value of h(x) is:
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25