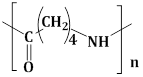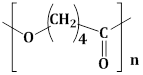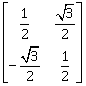Question Paper (Section wise)
-
1) An L-shaped object, made of thin rods of uniform mass density, is suspended with a string as shown in figure. If AB = BC, and the angle made by AB with downward vertical is θ, then:

-
-
2) A conducting circular loop made of a thin wire, has area 3.5 × 10-3 m2 resistance 10 Ω. It is placed perpendicular to a time dependent magnetic field B (t) = (0.4T) sin (50πt). The field is uniform in space. Then the net charge flowing through the loop during t = 0 s and t = 10 ms is close to:
-
0.14 mC
-
0.77 mC
-
0.21 mC
-
0.6 mC
-
-
3) A parallel plate capacitor is made of two square plates of side ‘a, separated by a distance d (d << a). The lower triangular portion is filled with a dielectric of dielectric constant K, as shown in the figure. Capacitance of this capacitor is
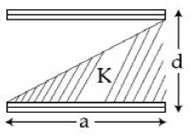
-
-
4) The Wheatstone bridge shown in Fig. here, gets balanced when the carbon resistor used as R1 has the colour code (Orange, Red, Brown) .The resistor R2 and R4 are 80 Ω, and 40 Ω, respectively. Assuming that the colour code for the carbon resistors, gives their accurate values, the colour code for the carbon resistor, used as R3 Would be
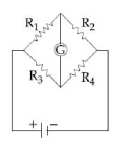
-
Brown, Blue, Brown
-
Brown, Blue, Black
-
Red, Green, Brown
-
Grey, Black, Brown
-
-
5) Half mole of an ideal monoatomic gas is heated at constant pressure of 1 atm from 20°C to 90°C. Work done by has is close to: (Gas constant R= 8.31J/mol.K)
-
581 J
-
291 J
-
146 J
-
73 J
-
-
6) Two kg of a monoatomic gas is at a pressure of 4 × 104 N/m2. The density of the gas is 8 kg/m3. What is the order of energy of the gas due to its thermal motion?
-
103 J
-
105 J
-
104 J
-
106 J
-
-
7) A satellite is revolving in a circular orbit at a height h from the earth surface, such that h << R where R is the radius of the earth. Assuming that the effect of earth’s atmosphere can be neglected the minimum increase in the speed required so that the satellite could escape from the gravitational field of earth is:
-
√2gR
-
√gR
-
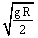
-
√gR(√2 - 1)
-
-
8) A particle is moving along a circular path with a constant speed of 10 ms–1. What is the magnitude of the change in velocity of the particle, when it moves through an angle of 60°+ around the centre of the circle?
-
10√3 m/s
-
0
-
10√2 m/s
-
10 m/s
-
-
9) An electromagnetic wave of intensity 50 Wm–2 enters in a medium of refractive index’ n’ without any loss . The ratio of the magnitudes of electric fields, and the ratio of the magnitudes of magnetic fields of the wave before and after entering into the medium are respectively. Given by:
-

-
(√n, √n)
-
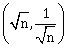
-
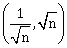
-
-
10) To double the covering range of a TV transition tower, its height should be multiplied by:
-
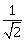
-
2
-
4
-
√2
-
-
11) A paramagnetic material has 1028 atoms/m3. Its magnetic susceptibility at temperature 350 K is 2.8 × 10-4. Its susceptibility at 300 K is:
-
3.267 × 10-4
-
3.672 × 10-4
-
3.726 × 10-4
-
2.672 × 10-4
-
-
12) Formation of real image using a biconvex lens is shown below:
If the whole set up is immersed in water without disturbing the object and the screen positions, what will one observe on the screen?
-
Image disappears
-
Magnified image
-
Erect real image
-
No change
-
-
13) In a simple pendulum experiment for determination of acceleration due to gravity (g), times taken for 20 oscillation is measured by using a watch of 1 second least count. The mean value of time the taken comes out to be 30s. The length of pendulum is measured by using a meter scale of least count 1 mm and the value obtained is 55.0 cm. percentage error in the determination of g is close to:
-
0.7%
-
3.5%
-
6.8%
-
0.2%
-
-
14) An electric dipole is formed by two equal and opposite charges q with separation d. The charges the same mass m. It is kept in a uniform electric field E. If it slightly rotated from its equilibrium orientation, then its angular frequency ω is:
-
-
15) A circuit connected to an as source of emf e = e0 sin (1000t) with t in seconds, gives a phase difference of
 between the emf e and current i. Which of the following circuits will exhibit this?
between the emf e and current i. Which of the following circuits will exhibit this?-
RC circuit with R = 1 k Ω and C = 1 μF
-
RL circuit with R = 1 k Ω and L = 10 mH
-
RL circuit with R = 1 k Ω and L = 1 mH
-
RC circuit with R = 1 kΩ and C = 10μF
-
-
16) A moving coil galvanometer has resistance 50 Ω and it indicates full deflection at 4mA current. A voltmeter is made using this galvanometer and a 5 kΩ resistance. The maximum voltage, that can be measured using this voltmeter, will be close to:
-
15 V
-
20 V
-
10 V
-
40 V
-
-
17) A concave mirror for face viewing has focal length of 0.4 m. The distance at which you hold the mirror from your face in order to see your image upright with a magnification of 5 is:
-
0.16 m
-
1.60 m
-
0.24 m
-
0.32 m
-
-
18) A string is clamed at both the ends and it is vibrating in its 4th harmonic. The equation of the stationary wave is Y =0.3 sin (0.157x) cos (200πt). The length of the string is: (all quantities are in SI units).
-
80 m
-
60 m
-
40 m
-
20 m
-
-
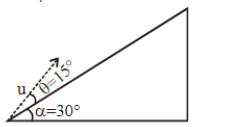
19) A plane is inclined at an angle α = 30° with respect to the horizontal. A particle is projected with a speed u = 2 ms-1, from the base of the plant, making an angle θ = 15° with respect to the plane as shown in the figure. The distance from the base at which the particle hits the plane is close to
Take g = 10 ms2
-
18 cm
-
14 cm
-
26 cm
-
20 cm
-
-
20) The time dependence of the position of a particle of mass m = 2 is given by
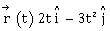 its angular momentum with respect to the origin at time t = 2 is
its angular momentum with respect to the origin at time t = 2 is -
-
21) A coil of self-inductance 10mH and resistance 0.1 Ω is connected through a switch to a battery of internal resistance 0.9 Ω. After the switch is closed the time taken for the current to attain 80% of the saturation values is ______ ms.
[ take ln5 = 1.6]
-
22) Two moles of helium gas is mixed with three moles of hydrogen molecules (taken to be rigid). The approximate value of molar specific heat of mixture at constant volume is ______.
(R = 8.3 J/mol K)
-
23) A shell is fired from a fixed artillery gun with an initial speed u such that it hits the target on the ground at a distance R form it. If t1 and t2 are the values of the time taken by it to hit the target in two possible ways, the product t1t2 is _____×
 .
. -
24) To concave mirror has radius of curvature of 40 cm. It is at the bottom of a glass that has water field up to 5 cm (see its figure). If a small particle is floating on the surface of water, its image as seen, from directly above the glass, is at a distance d from the surface of water. The value of d is close to _____ cm. (Refractive index of water = 1.33)

-
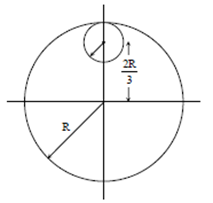
25) From a uniform circular disc of radius R and mass 9M, a small disc of radius
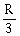 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is ______×I0.
is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is ______×I0.(Here, I0 = MR2)
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) Two complex [Cr(H2O)6]Cl3 (A) and [Cr(NH3)6]Cl3 (B) are violet and yellow coloured respectively. The incorrect statements regarding them is
-
Δ0 values of (A) and (B) are calculated from the energies of violet and yellow light, respectively.
-
both are paramagnetic with three unpaired electrons
-
both absorb energies corresponding to their complementary colours
-
Δ0 Value for (A) is less than that of (B)
-
-
2) Which one of the following statements regarding Henry’s law is not correct?
-
Higher the value of KH at a given pressure, higher is the solubility of the gas in the liquids
-
Different gases have different KH(Henry’s law constant) values at the same temperature
-
The partial pressure of the gas in vapour phase is proportional to the mole fraction of the gas in the solution
-
The value of KH increases with increase of temperature and KH is function of the nature of the gas.
-
-
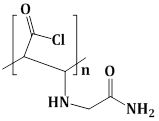
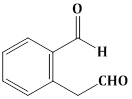
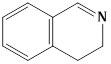
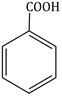
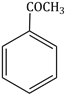
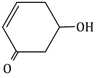
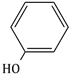
3) Major product of the following reaction is
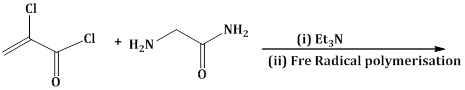
-
-
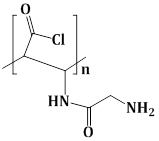
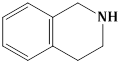
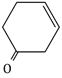
4) The major product of the following reaction is:
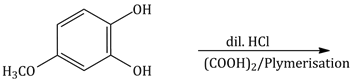
-
-
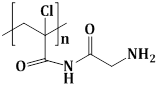
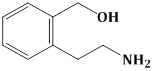
5) The major product of the following reaction is:
-
-
6) The minimum amount of O2(g) consumed per gram of reactant is for the reaction: (Given atomic mass : Fe = 56, O = 16, Mg = 24, P = 31, C = 12, H = 1)
-
C3H8(g) + 5O2(g) → 3 CO2(g) + 4 H2O(l)
-
P4(s) + 5O2(g) → P4O10(s)
-
4Fe(s) + 3O2(g) → 2 Fe2O3(s)
-
2 Mg(s) + O2(g) → 2 MgO(s)
-
-
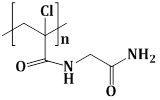
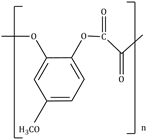
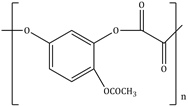
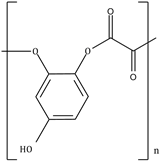
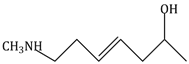
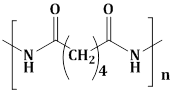
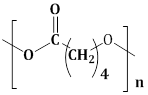
7) The polymer obtained from the following reaction is:

-
-
8) The major product of the following reaction is:
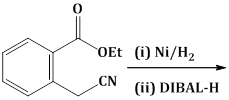
-
-
9) The chloride that cannot get hydrolysed is
-
PbCl4
-
CCl4
-
SnCl4
-
SiCl4
-
-
10) The correct sequence of thermal stability of the following carbonates is:
-
BaCO3 < SrCO3 < CaCO3 < MgCO3
-
BaCO3 < CaCO3 < SrCO3 < MgCO3
-
MgCO3 < CaCO3 < SrCO3 < BaCO3
-
MgCO3 < SrCO3 < CaCO3 < BaCO3
-
-
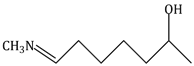
11) The aldehydes which will not form Grignard product with one equivalent Grignard reagents are:
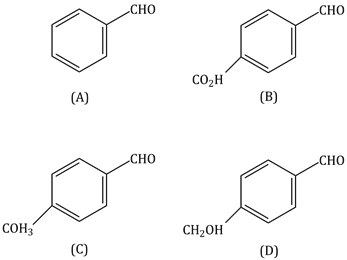
-
(b), (d)
-
(b), (c)
-
(b), (c), (d)
-
(c), (d)
-
-
12) The increasing order of the reactivity of the following with LiAIH4 is:
(a)
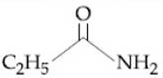
(b)

(c)
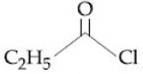
(d)

-
(b) < (a) < (c) < (d)
-
(b) < (a) < (d) < (c)
-
(a) < (b) < (d) < (c)
-
(a) < (b) < (c) < (d)
-
-
13) The ion that has sp3d2 hybridization for the central atom is
-
[lF6]⎺
-
[Icl4]⎺
-
[lCl2]⎺
-
[BrF2] ⎺
-
-
14) Which of the following is a thermosetting polymer?
-
PVC
-
Bakelite
-
Buna- N
-
Nylon 6
-
-
15) Which of the following statement is not true about RNA?
-
It has always double stranded α – helix structure
-
It is present in the nucleus of the cell
-
It controls the synthesis of protein
-
It usually does not replicate
-
-
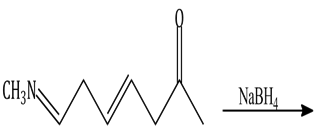
16) The major product of the following reaction is:
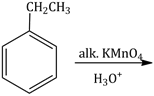
-
-
17) For a reaction, N2(g) + 3H2(g) → 2NH3(g);identify dihydrogen (H2) as a limiting reagent in the following reaction mixtures.
-
14g of N2 + 4g of H2
-
28g of N2 + 6g of H2
-
56g of N2 + 10g of H2
-
35g of N2 + 8g of H2
-
-
18) The major product of the following reaction is:
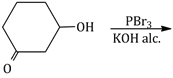
-
-
19) The correct statement is:
-
zincite is a carbonate ore
-
aniline is a froth stabilizer
-
zone refining process is used for the refining of titanium
-
sodium cyanide cannot be used in the metallurgy of silver
-
-
20) The correct option among the following is
-
Colloidal particles in lyophobic sols can be precipitated by electrophoresis.
-
Brownian motion in colloidal solution is faster the viscosity of the solution is very high.
-
Colloidal medicines are more effective because they have small surface area.
-
Addition of alum to water makes it unfit for drinking.
-
-
21) The number of 2-centre-2electron and 3-centre-3-electron bonds in B2H6, respectively, are 4 and ___.
-
22) Molecules of benzoic acid (C6H5COOH) dimerise in benzene. ‘w’ g of the acid dissolved in 30 g of benzene shows a depression in freezing point equal to 2 K. If the percentage association of the acid to form dimer in the solution is 80, then w in g is:
(Given that Kf = 5 K kg mol–1, Molar mass of benzoic acid = 122 g mol–1).
-
23) 0.27 g of a long chain fatty acid was dissolved in 100 cm3 of hexane. 10 mL of this solution was added dropwise to the surface of water in a round watch glass. Hexane evaporates and a monolayer is formed. The distance from edge to centre of the watch glass is 10 cm. The height in meter of the monolayer 10-x m and the x is
-
24) Among the following molecules / ions
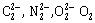 . How many are diamagnetic and has the shortest bond length?
. How many are diamagnetic and has the shortest bond length? -
25) How long (approximate) should water be electrolysed in hours by passing through 100 amperes current so that the oxygen released can completely burn 27.66 g of diborane? (Atomic weight of B = 10.8 u)
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) Equation of a common tangent to the circle, x2 + y2 - 6x = 0 and the parabola, y2 = 4x, is:
-
2√3 y = 12x + 1
-
√3 y = x + 3
-
2 √3 y = -x – 12
-
√3 y = 3x + 1
-
-
2) If A =
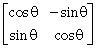 , then the matrix A-50 when θ =
, then the matrix A-50 when θ =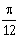 , is equal to:
, is equal to: -
-
3) Let α and β be two roots of the equation x2 + 2x + 2 = 0, then α15 + β15 is equal to:
-
–256
-
512
-
–512
-
256
-
-
4) Let
 . If R(z) and I(z) respectively denote the real and imaginary parts of z, then:
. If R(z) and I(z) respectively denote the real and imaginary parts of z, then:-
I(z) = 0
-
R(z) > 0 and I(z) > 0
-
R(z) < 0 and I(z) > 0
-
R(z) = –3
-
-
5) If mean and standard deviation of 5 observations x1, x2, x3, x4, x5 are 10 and 3 respectively, then the variance of 6 observations x1, x2… x5 and –50 is equal to:
-
509.5
-
586.5
-
582.5
-
507.5
-
-
6) Let a1, a2, a3,…, a10 be in G.P with ai > 0 for i = 1, 2, .., 10 and S be the set of pairs (r, k), r, k ϵ N (the set of natural numbers) for which
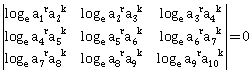
Then the number of elements in S, is
-
4
-
infinitely many
-
2
-
10
-
-
7) The plane containing the line
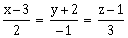 and also containing its projection on the plane 2x + 3y – z = 5, contains which one of the following points?
and also containing its projection on the plane 2x + 3y – z = 5, contains which one of the following points?-
(2, 2, 0)
-
(–2, 2, 2)
-
(0, –2, 2)
-
(2, 0, –2)
-
-
8) The maximum value of the function f(x) = 3x3 – 18x2 + 27x – 40 on the set S= {x ϵ R: x2 + 30≤ 11x} is
-
–122
-
–222
-
122
-
222
-
-
9) The sum of the real values of x for which the middle term in the binomial expansion of
 equals 5670 is:
equals 5670 is:-
0
-
6
-
4
-
8
-
-
10) 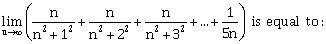
-

-
tan-1(3)
-
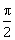
-
tan-1(2)
-
-
11) If a circle of radius R passes through the origin O and intersects the coordinate axes at A and B, then the locus of the foot of perpendicular from O on AB is:
-
(x2 + y2)2 = 4R2x2y2
-
(x2 + y2)3 = 4R2x2y2
-
(x2 + y2)2 = 4Rx2y2
-
(x2 + y2)(x + y) = R2xy
-
-
12) Let Z be the set of integers. If
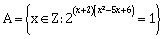 and B = {x ϵ Z: -3 < 2x – 1 < 9}, then the number of subsets of the set A × B, is:
and B = {x ϵ Z: -3 < 2x – 1 < 9}, then the number of subsets of the set A × B, is:-
215
-
218
-
212
-
210
-
-
13) If f(1)=1 and f’(1)=3, the derivative of f(f(f(x)))+(f(x))2 at x = 1 is:
-
33
-
15
-
9
-
12
-
-
14) The minimum number of times one has to toss a fair coin so that the probability of observing at least one head is at least 90% is:
-
2
-
3
-
4
-
5
-
-
15) Let the numbers 2, b, c be in an A.P and
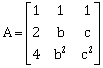 . If det (A)∊[2, 16] then c lies in the interval:
. If det (A)∊[2, 16] then c lies in the interval:-
[3, 2 + 23/4]
-
(2 + 23/4, 4)
-
[2, 3)
-
[4, 6]
-
-
16) A plane passing through the points (0, -1, 0) and (0, 0, 1) and making an angle
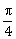 with plane y – z + 5 = 0, also passes through the point:
with plane y – z + 5 = 0, also passes through the point:-
(√2, 1, 4)
-
(-√2, -1, -4)
-
(-√2, 1, -4)
-
(√2, -1, 4)
-
-
17) The value of cos2 10° – cos 10° cos 50° + cos2 50° is:
-
-
18) Let S = {θ ϵ [-2π, 2π]: 2 cos2θ + 3 sin θ = 0}. Then the sum of the elements of S is:
-
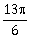
-
2π
-
Π
-
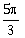
-
-
19) If 5x + 9 = 0 is the directrix of the hyperbola 16x2 – 9y2 = 144, then its corresponding focus is:
-
(5, 0)
-
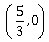
-
(–5, 0)
-
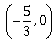
-
-
20) The tangent and normal to the ellipse 3x2 + 5y2 = 32 at the point P(2, 2) meet the x-axis at Q and R, respectively. Then the area (in sq. units) of the triangle PQR is:
-
-
21) Let λ be a real number for which the system of linear equations
x + y + z = 6
4x + λy – λz = λ – 2
3x + 2y – 4z = -5
has indefinitely many solutions. Then λ is equal to __________.
-
22) Let a random variable X have a binomial distribution with mean 8 and variance 4. If
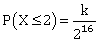 , then k is equal to:
, then k is equal to: -
23) If α and β are the roots of the equation 375x2 – 25x – 2 = 0, then
 is equal to:
is equal to: -
24) If A is a symmetric matrix and B is a skew-symmetrix matrix such that A + B =
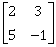 , then –|AB| is equal to:
, then –|AB| is equal to: -
25) For each t ϵ R, let [t] be the greatest integer less than or equal to t. Then
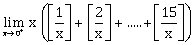 is equal to ______________.
is equal to ______________.
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25