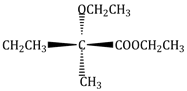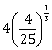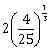Question Paper (Section wise)
-
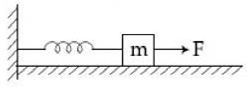
1) A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initially at rest in a equilibrium position. If now the block is pulled with a constant force F, the maximum speed of the block is
-
-
2) A block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3 N is applied on the block. The coefficient of static friction between the plane and the block is 0.6. What should be the minimum value of force P, such that the block does not move downward? (take g = 10 ms-2)

-
32 N
-
18 N
-
23 N
-
25 N
-
-
3) If the angular momentum of a planet of mass m, moving around the Sun in a circular orbit its L, about the canter of the Sun, its areal velocity is:
-
-
4) A particle which is experiencing a force, given by
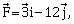 undergoes a displacement of.
undergoes a displacement of.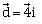 If the particle had a kinetic energy of 3 J at the beginning of the displacement, what is its kinetic energy at the end of the displacement?
If the particle had a kinetic energy of 3 J at the beginning of the displacement, what is its kinetic energy at the end of the displacement?-
9 J
-
12 K
-
10 J
-
15 J
-
-
5) For equal point charges Q each are placed in the XY plane at (0, 2), (4, 2), (4, - 2) and (0,-2). The work required to put a fifth charge Q at the origin of the coordinate system will be:
-
-
6) For the circuit shown below, the current through the Zener diode is:

-
9 mA
-
5 mA
-
Zero
-
14 mA
-
-
7) The given graph shows variation (with distance r from centre) of:

-
Electric field of a uniformly charged sphere
-
Potential of a uniformly charged spherical shell
-
Potential of a uniformly charged sphere
-
Electric field of a uniformly charged spherical shell
-
-
8) Equation of travelling wave on a stretched string of linear density 5 g/m is y = 0.03 sin (450 t – 9x) where distance and time are measured in SI united. The tension in the string is:
-
10N
-
7.5 N
-
12.5 N
-
5 N
-
-
9) In an experiment, electrons are accelerated, from rest, by applying, a voltage of 500 V. Calculate the radius of the path if a magnetic field 100 mT is then applied. [Charge of the electron = 1.6 × 10-19 C Mass of the electron = 9.1 × 10-31 kg]
-
7.5 × 10-3 m
-
7.5 ×10-2 m
-
7.5m
-
7.5 × 10-4 m
-
-
10) A load of mass M kg is suspended from a steel wire of length 2 m and radius 1.0 mm in searle’s apparatus experiment. The increase in length produced in the wire is 4.0 mm. Now the load is fully immersed in a liquid of relative density 2. The relative density of the material of load is 8.
The new value of increase in length of the steel wire is:
-
3.0 mm
-
4.0 mm
-
5.0 mm
-
Zero
-
-
11) In a radioactive decay chain, the initial nucleus is
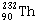 At the end there are 6 α- particles and 4β – particles with are emitted. If the end nucleus is
At the end there are 6 α- particles and 4β – particles with are emitted. If the end nucleus is 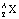 , A and Z are given by:
, A and Z are given by:-
A = 208; Z = 80
-
A = 202; Z = 80
-
A = 208; Z = 82
-
A = 200; Z = 81
-
-
12) When a certain photosensitive surface is illuminated with monochromatic light of frequency v, the stopping potential for the photo current is –V0/ 2. When the surface is illuminated by monochromatic light of frequency v/2, the stopping potential is –V0. The threshold frequency for photoelectric emission is:
-
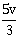
-
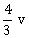
-
2 v
-
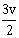
-
-
13) A solid sphere and solid cylinder of identical radii approach an incline with the same linear velocity (see figure). Both roll without slipping al throughout. The two climb maximum height hsph and hcyl on the incline. The radio
 is given by:
is given by:-
1
-
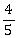
-
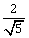
-
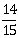
-
-
14) The ratio of mass densities of nuclei of 40Ca and 16O is closed to:
-
0.1
-
5
-
2
-
1
-
-
15) A nucleus A, with a finite de – broglie wavelength λA, undergoes spontaneous fission into two nuclei B and C of equal mass. B flies in the same direction as that of A, while C flies in the opposite direction with a velocity equal to half of that of F. The de – Broglie wavelength λB and λc of B and C are respectively:
-
λA, 2λA
-
2λA, λA
-
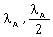
-
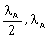
-
-
16) The electric field of light wave is given as.
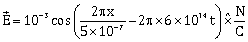 This light falls on a metal plate of work function 2eV. The stopping potential of the photoelectrons is
This light falls on a metal plate of work function 2eV. The stopping potential of the photoelectrons is-
0.48 V
-
2.48 V
-
0.72 V
-
2.0 V
-
-
17) A simple pendulum oscillating in air has period T. The bob of the pendulum is completely immersed in a non-viscous liquid. The density of the liquid is
 of the material of the bob. If the bob is inside liquid all the time, its period of oscillation in this liquid is:
of the material of the bob. If the bob is inside liquid all the time, its period of oscillation in this liquid is: -
-
18) A capacitor with capacitance 5 μF is charged to 5 μC. If the plates are pulled apart to reduce the capacitance to 2 μF, how much work is done?
-
3.75 × 10-6 J
-
2.55 × 10-6 J
-
6.25 × 10-6 J
-
2.16 × 10-6 J
-
-
19) Two radioactive substance A and B have decay constant 5λ and λ respectively. At t = 0, a sample has the same number of the two nuclei. The time taken for the ratio of the number of nuclei to become
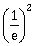 will be
will be-
1/λ
-
1/4λ
-
2/λ
-
1/2λ
-
-
20) Light is incident normally on a completely absorbing surface with an energy flux of 25 W cm-2. If the surface has an area of 25 cm2, the maximum transferred to the surface in 40 min time duration will be
-
6.3 × 10-4 Ns
-
3.5 × 10-6 Ns
-
5.0 × 10-3 Ns
-
1.4 × 10-6 Ns
-
-
21) A submarine experiences a pressure of 0.5 × 106 Pa at a depth of d1 in a sea. When it goes further to a depth of d2, it experiences a pressure of 8.08 × 106 Pa. Then d2 –d1 is approximately ________ m.
(Density of water = 103 kg/m3 and acceleration due to gravity = 10 ms-2)
-
22) At 40° C, a brass wire of 1 mm is hung from the ceiling. A small mass, M is hung from the free end of the wire. When the wire is cooled down from 40°C to 20°C it regains its original length of 0.2 m. The value of M is close to ______ kg.
(Coefficient of linear expansion and Youngs modules of brass are 10-5/°C and 1011 N/m2, respectively; g = 10 ms-2).
-
23) Two batteries with e.m.f 12 V and 13 V are connected in parallel across a load resistor of 10 Ω. The internal resistances of the two batteries are 1 Ω and 2 Ω respectively. The voltage across the load will be approximately _______ V.
-
24) A satellite orbits around a planet at a height of 20 km from surface. Assuming that only gravitational field of the plant acts on the spaceship. The approximate number of revolution made by the satellite in 12 hours around the plane is ______.
[Given: Mass of plane = 8 × 1022 kg, Radius of planet = 2 × 106 m, Gravitational constant G = 6.67 × 10-11 Nm2/kg2]
-
25) A parallel plate capacitor has 1μF capacitance. One of its two plates is given + 2μC charge and the other plate, +4μC charge. The potential difference developed across the capacitor is ________ V.
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
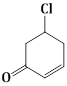
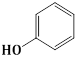
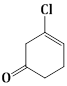
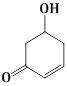
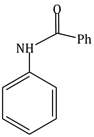
1) The major product of the following reaction is
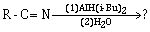
-
RCOOH
-
RCONH2
-
RCHO
-
RCH2NH2
-
-
2) The one that is extensively used as a piezoelectric material is
-
tridymite
-
amorphous silica
-
quartz
-
mica
-
-
3) Which amongst the following is the strongest acid?
-
CHBr3
-
CHI3
-
CH(CN)3
-
CHCI3
-
-
4) The correct match between item ‘I’ and item ‘II’ is:
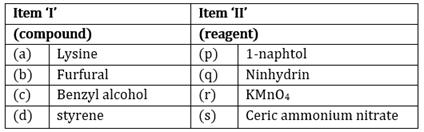
-
(a)→(q); (b) → (p); (c) × (s); (d) → (r)
-
(a) → (q); (b) → (p); (c) → (r); (d) → (s)
-
(a) → (r); (b) → (p); (c) → (q); (d) → (s)
-
(a) → (q); (b) → (r); (c) → (s); (d) → (p)
-
-
5) The pair that contains two P – H bonds in each of the oxoacids is:
-
H4 P2 O5 and H4 P2 O6
-
H3 PO2 and H4 P2 O5
-
H3 PO3 and H3 PO2
-
H4 P2 O5 and H3 PO3
-
-
6) Which is the most suitable reagent for the following transformation?

-
Tollen’s reagent
-
l2 /NaOH
-
CrO2Cl2 / Cs2
-
alkaline KMnO4
-
-
7) The highest possible oxidation states of uranium and plutonium, respectively, are
-
6 and 4
-
7and 6
-
4 and 6
-
6 and 7
-
-
8) The element the usually does NOT show variable oxidation states is:
-
Cu
-
Ti
-
Sc
-
V
-
-
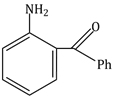
9) The major product of the following reaction is:
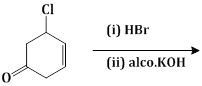
-
-
10) The major product of the following reaction is:
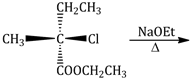
-
-
11) The two monomers for the synthesis Nylon 6, 6 are:
-
HOOC (CH2)4COOH, H2N (CH2)6NH2
-
HOOC (CH2)6COOH, H2N (CH2)6NH2
-
HOOC (CH2)4COOH, H2N (CH2)4NH2
-
HOOC (CH2)6COOH, H2N (CH2)4NH2
-
-
12) The pair that does NOT require calcination is:
-
ZnO and MgO
-
ZnO and Fe2O3.xH2O
-
ZnCO3 and CaO
-
Fe2O3 and CaCO3.MgCO3
-
-
13) For a reaction scheme,
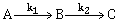 if the rate formation of B is set to be zero then the concentration of B given by
if the rate formation of B is set to be zero then the concentration of B given by-
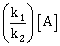
-
(k1 - k2)[A]
-
k1k2[A]
-
(k1 + k2)[A]
-
-
14) Given:
Co3+e-→ Co2+; E° = 1.81 V
Pb4 + 2e-→ Pb2+; E° = +1.67V
Ce4+ + e-→ Ce3+; E° + 1.61 V
Bi3+ + 3e-→ Bi; E° = +0.20 V
Oxidising power of the species will increase in the order
-
Ce4+ < Pb4+ < Bi3+ < Co3+
-
Co3+ < Pb4+ < Ce4+ < Bi3+
-
Bi3+ < Ce4+ < Pb4+ < Co3+
-
Co3+ < Ce4+ < Bi3+ < Pb4+
-
-
15) But-2-ene on reaction with alkaline KMnO4 at elevated temperature followed by acidification will give:
-
One molecule of CH3CHO and molecule of CH3COOH
-
2 molecules of CH3CHO
-
2 molecules of CH3COOH
-
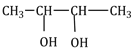
-
-
16) The major product of the following reaction is:
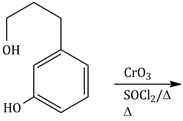
-
-
17) The correct order of the oxidation states of nitrogen in NO, N2O, NO2 and N2O3 is:
-
N2O < N2O3 < NO < NO2
-
NO2 < NO < N2O3 < N2O
-
NO2 < N2O3 < NO < N2O
-
N2O < NO < N2O3 < NO2
-
-
18) Hydrogen peroxide oxidises [Fe(CN)6]4− to [Fe(CN)6]3− in acidic medium but reduces [Fe(CN)6]3− to [Fe(CN)6]4− in alkaline medium. The order product formed are, respectively
-
H2O and (H2O + OH−)
-
(H2O +O2) and H2O
-
(H2O +O2) and (H2O + OH−)
-
H2O and (H2O +O2)
-
-
19) Which of these factors does not govern the stability of a conformation in acyclic compounds?
-
Torsional strain
-
Angle strain
-
Steric interactions
-
Electrostatic forces of interaction
-
-
20) The major product 'Y' in the following reaction is:-
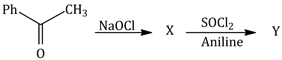
-
-
21) A solid having density of 9 × 103 kg m-3forms face centred cubic crystal of edge length
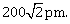
The molar mass of the solid is ______ kg mol-1
[Avogadro constant ≅ 6 × 1023 and mol-1≅ 3]
-
22) 5 moles of an ideal gas at 100 K are allowed to undergo reversible compression till its temprature becomes 200 K. If Cv = 28 JK-1 mol-1, calculate ΔU for this process.(R = 8.0 J K-1 mol-1)
-
23) The maximum prescribed concentration of copper in drinking water is_____ ppm.
-
24) The osmotic pressure of a dilute solution of an ionic compound XY in water is four times that of a solution of 0.01 M BaCl2 in water. Assuming complete dissociation of the given ionic compounds in water ,the concentration of XY (in mol L-1) in solution is
-
25) The standard Gibbs energy for the given cell reaction in kJ mol-1 at 298 K is:
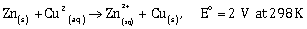
[Faraday’s constant F = 96000 C/mol].
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
-
1) 5 students of a class have an average height 150 cm and variance 18 cm2. A new student, whose height is 156 cm, joined them. The variance (in cm2) of the height of these six students is:
-
16
-
22
-
20
-
18
-
-
2) 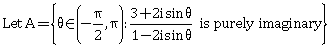 Then the sum of the elements in A is:
Then the sum of the elements in A is:-

-
π
-
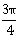
-
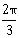
-
-
3) Consider a class of 5 girls and 7 boys. The number of different teams consisting of 2 girls and 3 boys that can be formed from this class, if there are two specific boys A and B, who refuse to be the members of the same team, is:
-
500
-
200
-
300
-
350
-
-
4)  , then f’ (1/2) is :
, then f’ (1/2) is : -
-
5) Consider the following three statements:
P : 5 is a prime number
Q : 7 is a factor of 192
R : L.C.M of 5 and 7 is 35
Then the truth value of which one of the following statements is true?
-
(~P) ˅ (Q ˄ R)
-
(P ˄ Q) ˅ (~R)
-
(~P) ˄ (~Q ˄ R)
-
P ˅ (~Q ˄ R)
-
-
6) 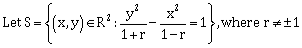 Then S represents:
Then S represents:-
a hyperbola whose eccentricity is
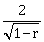 , when 0 < r <1.
, when 0 < r <1. -
an ellipse whose eccentricity is
 , when r > 1.
, when r > 1. -
a hyperbola whose eccentricity is
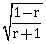 , when 0 < r < 1.
, when 0 < r < 1. -
an ellipse whose eccentricity is
 , when r > 1.
, when r > 1.
-
-
7) If y(x) is the solution of the differential equation
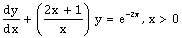 where y(1)
where y(1)  , then:
, then:-
y (loge 2) = loge 4
-
y (loge 2)
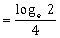
-
y (x) is decreasing in
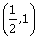
-
y (x) is decreasing in (0, 1)
-
-
8) The direction ratio of normal to the plane through the points (0, -1, 0) and (0, 0, 1) and making an angle
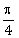 with the plane y – z + 5 = 0 is :
with the plane y – z + 5 = 0 is :-
2, -1, 1
-
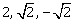
-
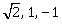
-
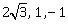
-
-
9) 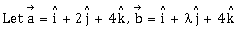 and
and  be coplanar vectors. Then the non – zero vector
be coplanar vectors. Then the non – zero vector 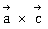 is:
is: -
-
10) Let f be a differentiable function such that f(1) = 2 and f ’(x) = f(x) for all x ∈ R. If h(x) = f(f(x)), then h’(1) is equal to :
-
2e2
-
4e
-
2e
-
4e2
-
-
11) The set of all values of λ for which the system of linear equations
x – 2y – 2z =λx
x + 2y + z = λy
–x – y = λz,
has a non-trivial solution :
-
is a singleton
-
contains exactly two elements
-
is an empty set
-
contains more than two elements
-
-
12) If nC4, nC5 and nC6 are in A. P., then n can be:
-
9
-
14
-
11
-
12
-
-
13) Let S(λ) = {(x, y): y2≤ 4x, 0 ≤ x ≤ λ} and A(λ) is the area of the region S(λ). If for λ, 0 < λ < 4, A(λ) : A(4) = 2:5 then λ equals:
-
-
14) If the lengths of the sides of a triangle are in A.P. and the greatest angle is double the smallest, then a ratio of lengths of the sides of this triangle is:
-
4 : 5 : 6
-
5 : 6 : 7
-
3 : 4 : 5
-
5 : 9 : 13
-
-
15) Let f: R→R be a differentiable function satisfying
f’(3) + f’(2) = 0. Then
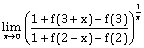 is equal to:
is equal to:-
e2
-
1
-
e
-
e-1
-
-
16) If the fourth term in the Binomial expansion of
 is 20 × 87, then the value of x is:
is 20 × 87, then the value of x is:-
83
-
8-2
-
8
-
82
-
-
17) The value of
 dx is:
dx is: -
-
18) Four persons can hit a target correctly with probabilities
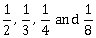 respectively. If all hit at the target independently, then the probability that the target would be hit, is:
respectively. If all hit at the target independently, then the probability that the target would be hit, is: -
-
19) The locus of the centres of the circles, which touch the circle, x2 + y2 = 1 externally, also touch the y-axis and lie in the first quadrant is :
-
-
20) The number of real roots of the equation 5+|2x-1|=2x(2x-2) is:
-
4
-
3
-
2
-
1
-
-
21) If the of the series
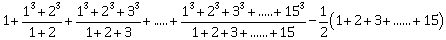
is p, then
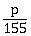 is equal to _________.
is equal to _________. -
22) 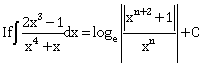 then n is equal to ______.
then n is equal to ______.(Here C is a constant of integration)
-
23) If m is the minimum value of k for which the function
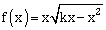 is increasing in the interval [0, 3] and M is the maximum value of f in [0, 3] when k = m, then the value of (m2 + M2 – 40) is equal to ________.
is increasing in the interval [0, 3] and M is the maximum value of f in [0, 3] when k = m, then the value of (m2 + M2 – 40) is equal to ________. -
24) If the angle of intersection at a point where the two circles with radii 5 cm and 12 cm intersect is 90∘, such that the length (in cm) of their common chord is
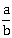 cm, then (a – 9b) is equal to _____________.
cm, then (a – 9b) is equal to _____________. -
25) A bag contains 4 red and 6 black balls. A ball is drawn at random from the bag. Its colour is observed and this ball along with two additional balls of the same colour are returned to the bag. Now, if a ball is drawn at random from the bag and the probability of getting this ball as red comes out to be
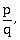 then p + q is equal to _________
then p + q is equal to _________
-
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
-
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25