Sequences and Series
Sequence and Series PDF Notes, Important Questions and Synopsis
SYNOPSIS
- A sequence is an ordered list of numbers and has the same meaning as in conversational English. A sequence is denoted by <an>(n ≥ 1) = a1,a2,a3, … an.
- The various numbers occurring in a sequence are called its terms.
- A sequence containing finite number of terms is called a finite sequence. A finite sequence has a last term.
- A sequence which is not a finite sequence, i.e. containing infinite number of terms is called an infinite sequence. There is no last term in an infinite sequence.
- A sequence is said to be an arithmetic progression if every term differs from the preceding term by a constant number. For example, the sequence a1, a2, a3,… an is called an arithmetic sequence or an AP if an+1 = an + d, for all n Î N, where ‘d’ is a constant called the common difference of the AP.
- ‘A’ is the arithmetic mean of two numbers ‘a’ and ‘b’ if form an arithmetic progression.
- A sequence is said to be a geometric progression or GP if the ratio of any of its terms to its preceding term is the same throughout. A constant ratio is the common ratio denoted by ‘r’.
- If three numbers are in GP, then the middle term is called the geometric mean of the other two.
- Some Concepts
- A sequence has a definite first member, second member, third member and so on.
- The nth term <an> is called the general term of the sequence.
-
Fibonacci sequence 1, 1, 2, 3, 5, 8,… is generated by the recurrence relation given by
a1 = a2 = 1
a3 = a1 + a2…
an = an-2 + an-1, n > 2 -
If the number of terms are three with common difference 'd', then the three terms can be taken as a – d, a, a + d.
-
If the number of terms are four with common difference '2d', then the terms can be taken as a – 3d, a – d, a + d, a + 3d.
-
If the number of terms are five with common difference 'd', then the terms can be taken as a – 2d, a – d, a, a + d, a + 2d.
-
If the number of terms are six with common difference '2d', then the terms can be taken as a – 5d, a – 3d, a – d, a + d, a + 3d, a + 5d.
-
General form of an AP is a, a + d, a + 2d,… a + (n - 1)d, where ‘a’ is called the first term of the AP and ‘d’ is called the common difference of the AP. ‘d’ can be any real number.
-
If d > 0, then the AP is increasing. If d < 0, then the AP is decreasing. If d = 0, then the AP is constant.
-
If ‘a’ is the first term and ‘d’ is the common difference of an AP with 'm' terms, then the nth term from the end is the
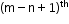 term from the beginning.
term from the beginning. -
General term of a GP is arn-1, where ‘a’ is the first term and r is the common ratio.
-
If the number of terms of a GP is 3 with the common ratio r, then the selection of terms can be
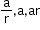 .
. -
If the number of terms of a GP is 4 with the common ratio r2 , then the selection of terms can be
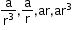
-
If the number of terms of a GP is 5 with the common ratio r, then the selection of terms can be
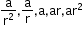
- If a constant is added to each term of an AP, then the resulting sequence is also an AP.
-
If a constant is subtracted from each term of an AP, then the resulting sequence is
also an AP. -
If each term of an AP is multiplied by a constant, then the resulting sequence is also an AP.
-
If each term of an AP is divided by a non-zero constant, then the resulting sequence is also an AP.
-
The arithmetic mean A of any two numbers ‘a’ and ‘b’ is given by
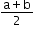
-
General form of a GP is a, ar, ar2, ar3…, where ‘a’ is the first term and ‘r’ is the constant ratio which can be any non-zero real number.
-
A sequence in geometric progression will remain in geometric progression if each of its terms is multiplied by a non-zero constant.
-
A sequence obtained by multiplying two GPs term by term will result in a GP with a common ratio as the product of the common ratios of the two GPs.
-
Reciprocals of the terms of a given GP form a GP with the common ratio
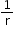
-
If each term of a GP is raised to the same power, then the resulting sequence also forms a GP.
-
The geometric mean (GM) of any two positive numbers ‘a’ and ‘b’ is given by
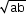
Some Special Series
- Sum of the first ‘n’ natural numbers:
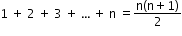
- Sum of the squares of the first n natural numbers:
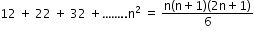
- Sum of the cubes of the first n natural numbers:
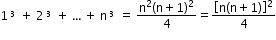
- Sum of the powers of 4 of the first n natural numbers:
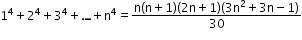
Related Chapters
- Sets, Relations and Functions
- Complex Numbers and Quadratic Equations
- Matrices and Determinants
- Permutations and Combinations
- Mathematical Induction
- Binomial Theorem and its Simple Applications
- Limit, Continuity and Differentiability
- Integral Calculus
- Differential Equations
- Co-ordinate Geometry
- Three Dimensional Geometry
- Vector Algebra
- Statistics and Probability
- Trigonometry
- Mathematical Reasoning