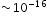Physics and Measurement

Physics and Measurement PDF Notes, Important Questions and Synopsis

SYNOPSIS

Macroscopic domain: This includes phenomena at the laboratory, terrestial and astronomical scales. Classical mechanics deals with the macroscopic domain.
Microscopic domain: This includes atomic, molecular and nuclear phenomena. Quantum mechanics deals with the microscopic domain.

Force	Relative strength	Range
Gravitational force	10^-39	Infinite
Nuclear force (weak)	10^-13	Very short, sub-nuclear size $begin mathsize 12px style text ∼10 end text to the power of negative 16 end exponent end style$
Electromagnetic force	10^-2	Infinite
Nuclear force (strong)	1	Short, nuclear size $begin mathsize 12px style text ∼10 end text to the power of negative 16 end exponent end style$

Physical quantities:
Measure of physical quantity (Q) = numerical value of physical quantity (n) × size of unit (u) n₁u₁ = n₂u₂ = constant

Fundamental quantities, SI unit and their symbols:

Conversion of units:
Consider dimensions of a physical quantity as ‘x’ in mass, ‘y’ in length and ‘c’ in time. If the fundamental units in one system are M₁, L₁ and T₁ and in another system are M₂, L₂ and T₂,
then
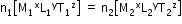
$begin mathsize 12px style text n end text subscript 1 open square brackets straight M subscript 1 to the power of straight x straight L subscript 1 to the power of straight y straight T subscript 1 to the power of straight z close square brackets straight equals straight straight n subscript 2 open square brackets straight M subscript 2 to the power of straight x straight L subscript 2 to the power of straight y straight T subscript 2 to the power of straight z close square brackets end style$
Analysis of dimensional correctness:
Every equation should be dimensionally balanced. This is called ‘principle of homogeneity’. The dimensions of each term must be the same on both sides of the equation.
Principle of homogeneity:
According to the principle of homogeneity, dimensions of all terms in a physical expression should be the same.
Errors:
Errors are classified as (i) systematic errors and (ii) random errors.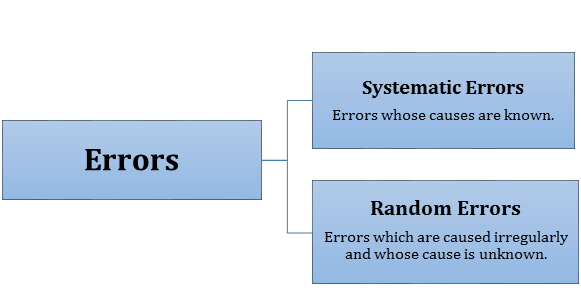

If x₁, x₂, x₃ … xn are the measured values of quantities in several measurements, then the mean is

$begin mathsize 12px style text x end text subscript mean equals fraction numerator straight x subscript 1 plus straight x subscript 2 plus straight x subscript 3. .. straight x subscript straight n over denominator straight n end fraction end style$
Absolute errors in measured values are
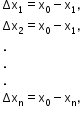
$begin mathsize 12px style table attributes columnalign left end attributes row cell Δx subscript 1 equals straight x subscript 0 minus straight x subscript 1 comma end cell row cell Δx subscript 2 equals straight x subscript 0 minus straight x subscript 1 comma end cell row. row. row. row cell Δx subscript straight n equals straight x subscript 0 minus straight x subscript straight n comma end cell end table end style$
If the quantity Z is expressed as a product of quantities A and B, then the maximum fractional error in Z is given by
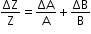
$begin mathsize 12px style ΔZ over straight Z equals ΔA over straight A plus ΔB over straight B end style$
If Z = AxByCz, then the maximum fractional error in Z is
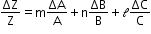
$begin mathsize 12px style ΔZ over straight Z equals straight m ΔA over straight A plus straight n ΔB over straight B plus calligraphic l ΔC over straight C end style$