Magnetic Effects of Current and Magnetism
Magnetic Effects of Current and Magnetism PDF Notes, Important Questions and Synopsis
SYNOPSIS
- Lorentz force: Force on a charge q moving with velocity v in the presence of magnetic and electric fields B and E.
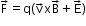
- The magnetic force
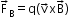 is normal to
is normal to 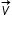 and work done by it is zero.
and work done by it is zero. - Force F on a straight conductor of length 𝓁 and carrying a steady current I placed in a uniform external magnetic field B,
 In a uniform magnetic field the force, dF = IBdl Sinθ, does not depend on the position vector r of the current element.Thus, this force is non-central. The force
In a uniform magnetic field the force, dF = IBdl Sinθ, does not depend on the position vector r of the current element.Thus, this force is non-central. The force  is always perpendicular to the plane containing
is always perpendicular to the plane containing 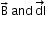
- Biot–Savart law asserts that the magnetic field
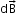 due to an element
due to an element 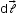 carrying a steady current I at a point P at a distance r from the current element is
carrying a steady current I at a point P at a distance r from the current element is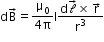
- The magnetic field due to a circular coil of radius R carrying a current I at an axial distance x from the centre is
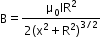
At the centre of the coil,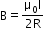
- Ampere’s circuital law: For an open surface S bounded by a loop C,
 , where I refers to the current passing through S.
, where I refers to the current passing through S.
If B is directed along the tangent to every point on the perimeter, then
Where Ie is the net current enclosed by the closed circuit. Ampere’s law is an important tool in calculating the magnetic field due to current distribution. However, this usefulness is limited to only a few cases where the magnetic field has a symmetrical distribution in space. For example, this law cannot be used to find the magnetic field at the centre of a current-carrying loop. Ampere’s circuital law is not an independent law, but it is derived from Biot–Savart law - The magnetic field at a distance R from a long, straight wire carrying a current I is given by
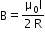
The field lines are circles concentric with the wire. - Magnetic field B inside a long solenoid carrying a current I is
B = μ0 nI
where n is the number of turns per unit length.
For a toriod,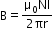
where N is the total number of turns and r is the average radius. -
Magnetic moment m of a planar loop carrying a current I with N closely wound turns and an area A is
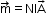
Direction of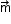 is given by the right-hand thumb rule.
is given by the right-hand thumb rule.
Right-hand thumb rule: Curl the palm of your right hand along the loop with the fingers pointing in the direction of the current. The thumb sticking out gives the direction of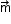 (and
(and 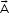 ).
).
When this loop is placed in a uniform magnetic field B, the force F on it is F = 0
and the torque on it is
In a moving coil galvanometer, this torque is balanced by a counter torque due to a spring yielding
kϕ = NI AB
Where ϕ is the equilibrium deflection and k is the torsion constant of the spring.
Uses of a moving coil galvanometer:
- It is used to detect electric current in a circuit, e.g. Wheatstone Bridge.
- It is converted to an ammeter by putting a small resistance parallel to it.
- It is used as an ohmmeter.
-
An electron moving around the central nucleus has a magnetic moment
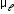 given by
given by
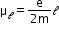
Where 𝓁 is the magnitude of the angular momentum of the circulating electron about the central nucleus. The smallest value of μ𝓁 is called the Bohr magneton μB, and it is μB = 9.27 × 10–24 J/T. -
Cyclotron:
A cyclotron is a device used to accelerate positively charged particles (like protons, α-particles, deuterons, ions etc.) to acquire enough energy to carry out nuclear disintegration.
A charge q executes a circular motion with frequency called the cyclotron frequency given by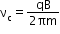
This cyclotron frequency is independent of the particle’s speed and radius.
Time period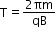
Radius
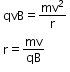
Limitations of a cyclotron:
A cyclotron cannot accelerate uncharged particles like neutrons. Positively charged particles with large mass (i.e. ions) cannot be accelerated after a certain speed in the cyclotron. -
Magnetic materials tend to point in the north–south direction.
Like magnetic poles repel and unlike poles attract each other.
Cutting a bar magnet in two leads to two smaller magnets.
Magnetic poles cannot be isolated. -
When a bar magnet of dipole moment
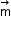 is placed in a uniform magnetic field
is placed in a uniform magnetic field 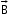 ,
,
- The force on it is zero.
- The torque on it is
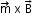 .
. - Its potential energy is
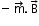 , where we choose the zero of the energy at the orientation when is perpendicular to .
, where we choose the zero of the energy at the orientation when is perpendicular to .
-
Consider a bar magnet of size 𝓁 nd magnetic moment
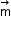 at a distance r from its midpoint, where r >>𝓁; the magnetic field
at a distance r from its midpoint, where r >>𝓁; the magnetic field 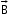 due to this bar is
due to this bar is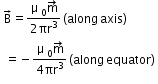
-
Gauss’s law for magnetism: The net magnetic flux through any closed surface is zero.

-
Curie’s law: According to Curie’s law, the susceptibility of a paramagnetic substance is inversely proportional to the absolute temperature: m = c/T, where c is a constant called the Curie constant.
-
The pole near the geographic north pole of the Earth is called the north magnetic pole.
The pole near the geographic south pole is called the south magnetic pole.
The magnitude of the magnetic field on the Earth’s surface = 4 × 10−5 T. -
Three quantities are needed to specify the magnetic field of the Earth on its surface—the horizontal component, the magnetic declination and the magnetic dip.
These are known as the elements of the Earth’s magnetic field. -
Consider a material placed in an external magnetic field
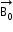
The magnetic intensity is defined as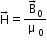
The magnetisation
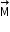 of the material is its dipole moment per unit volume.
of the material is its dipole moment per unit volume.
The magnetic field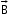 in the material is
in the material is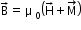
For a linear material
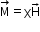 So,
So,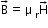
where
𝓍: Magnetic susceptibility of the material
μr: Relative magnetic permeability
The relative magnetic permeability μr and the magnetic permeability μ are related as follows:μ = μ0 μr
μr = 1 +𝓍 -
Magnetic materials are broadly classified as diamagnetic, paramagnetic and ferromagnetic.
For diamagnetic materials, 𝓍 is negative and small.
For paramagnetic materials, 𝓍 is positive and small.
For ferromagnetic materials, 𝓍 is positive and large. -
Substances which at room temperature retain their ferromagnetic property for a long period of time are called permanent magnets.
-
HYSTERESIS
If a ferromagnetic material is magnetised in one direction and the applied magnetising field is removed, then its magnetisation will not be reduced to zero. It must be driven back to zero by a field in the opposite direction. If an alternating magnetic field intensity is applied to the material, its
magnetisation will trace out a loop called a hysteresis loop. The phenomenon in which magnetic flux density (B) lags behind the magnetising field (H) in a ferromagnetic material during cycles of magnetisation is called hysteresis
Related Chapters
- Physics and Measurement
- Kinematics
- Laws of Motion
- Work, Energy and Power
- Rotational Motion
- Gravitation
- Properties of Solids and Liquids
- Thermodynamics
- Kinetic Theory of Gases
- Oscillations and Waves
- Electrostatics
- Current Electricity
- Electromagnetic Induction and Alternating Currents
- Electromagnetic Waves
- Optics
- Dual Nature of Matter and Radiation
- Atoms and Nuclei
- Electronic Devices
- Communication Systems