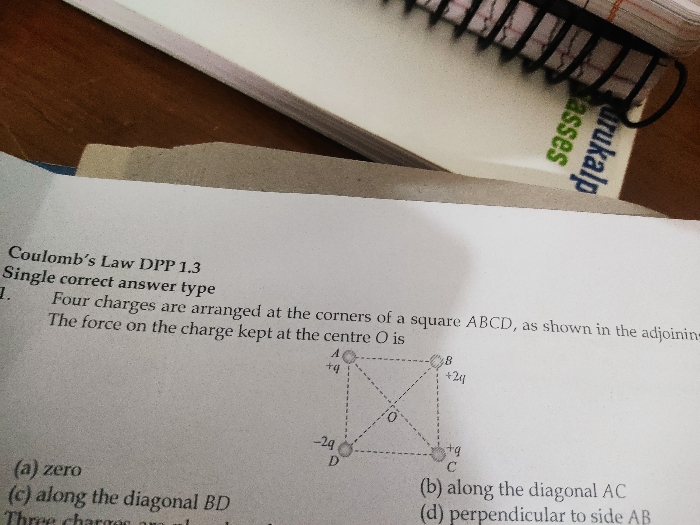Electrostatics
Electrostatics PDF Notes, Important Questions and Synopsis
SYNOPSIS
- Electric charge: The property associated with matter due to which it produces and experiences electric and magnetic fields.
- Properties of charge: Transferable, always associated with mass, conserved, quantised.
- Methods of charging of a body: Conduction, induction, friction
- Coulomb’s law:

Not valid for distance less than .10-2
Electrostatic force is conservative in nature.
Valid only for point charges.
- Superposition principle: The total force on a given charge is the vector sum of all the individual forces exerted by each of the other charges.
- Electric field: The space around the charge in which its influence can be felt by any other charged particle.
A point charge in an electric field experiences force .
For positive source charge, the electric field is radially outward, whereas for negative source charge, the electric field is radially inward.
A positive charge placed in an electric field experiences force in the same direction as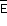 , while a negative charge experiences force in the opposite direction as
, while a negative charge experiences force in the opposite direction as 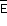 .
. - Properties of lines of force: The strength of the electric field is directly proportional to the density of lines of force.
Electric field within a conductor is zero. - Electric dipole:
It is a system of two equal and opposite point charges separated by a very small and finite distance. The strength of an electric dipole is measured by electric dipole moment p = 2ql; the direction is from –q to +q.
Electric field due to a dipole at some general point is given by , where is the angle between the axis of the dipole and the line joining point P and the axis.
, where is the angle between the axis of the dipole and the line joining point P and the axis. -
Dipole in uniform electric field:
Net force on a dipole in a uniform electric field is zero.
Torque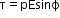 , torque is maximum when the dipole is perpendicular
, torque is maximum when the dipole is perpendicular 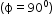 to the field and minimum when the dipole is parallel
to the field and minimum when the dipole is parallel 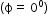 or antiparallel
or antiparallel  to the field.
to the field. -
Dipole in non-uniform electric field:
The net force depends on
Orientation of the dipole, dipole moment of the dipole and how rapidly the field varies. -
Electric flux:
The product of magnitude of electric field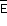 and surface area A perpendicular to the field is called electric flux
and surface area A perpendicular to the field is called electric flux 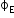 .
. 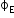 depends on both field pattern and surface. The net flux is directly proportional to the net number of lines leaving the surface.
depends on both field pattern and surface. The net flux is directly proportional to the net number of lines leaving the surface. -
Gauss’s law:
Electric flux through a closed surface S is given by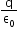 , where q is the charge enclosed by surface S.
, where q is the charge enclosed by surface S.
The net field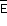 is due to all charges present inside and outside the Gaussian surface. No net flux is contributed by the charges present outside the Gaussian surface because the number of E-lines coming into the surface is equal to the number of E-lines going out of the surface.
is due to all charges present inside and outside the Gaussian surface. No net flux is contributed by the charges present outside the Gaussian surface because the number of E-lines coming into the surface is equal to the number of E-lines going out of the surface. -
Electric field due to a charged isolated plate:
The electric field due to a charged isolated plate is twice the field due to a plane sheet of charge .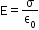 The electric field due to an infinitely charged plate does not depend on the distance from the plate.
The electric field due to an infinitely charged plate does not depend on the distance from the plate. -
Electric potential:
The potential at a point P is given by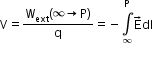 , which is equal to the external work done per unit positive charge in shifting slowly from infinity to this point.
, which is equal to the external work done per unit positive charge in shifting slowly from infinity to this point.
In the direction of electric field, the potential always decreases.
Potential is a scalar quantity. Its SI unit is volt.

-
Equipotential surface:
An equipotential surface is a surface with constant value of potential at all points on the surface. The equipotential surface of a single point charge are concentric spherical surfaces centred at the charge. For uniform electric field, equipotential surfaces are planes normal to the plane of the electric field. -
Potential energy of a system of charges:
For two charges,
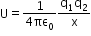
For three charges,
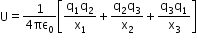
For discreet system of charges,
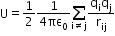
General formula for calculating potential energy: U = qV, where V is the potential at a point of some continuous body (ring, disc, solid sphere etc.).
-
Finding electric field from electric potential:
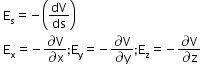
-
Earthing of a conductor:
On earthing a conductor, the charge on the conductor varies and the potential of the conductor becomes zero. -
Charge distribution on a conductor surface:
The charge distribution takes place on the surface of the conductor in such a way that the product of charge density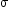 and the radius of curvature r at any point on the conductor is constant, i.e.
and the radius of curvature r at any point on the conductor is constant, i.e.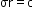
-
Dielectrics are non-conducting substances. They have no charge carriers.
- The molecules of a substance may be polar or non-polar.
- In a non-polar molecule, the centres of positive and negative charges coincide. Thus, the molecule does not have any permanent dipole moment.
In a polar molecule, the centres of positive and negative charges are separated. These molecules have a permanent dipole moment.
Introduction of dielectrics develops a net dipole moment in the substance whether polar or non-polar. - Capacitance is determined purely geometrically, by the shapes, sizes and relative positions of the two conductors.
- Changes observed when the medium between the plates of a capacitor is filled with an insulating substance (dielectric):
- Polarization of the medium gives rise to a field in the opposite direction. The net electric field inside the insulating medium is reduced.
- Potential difference between the plates is thus reduced.
- Capacitance C increases from its value C0 when there is no medium (vacuum).
C = KC
Where K is the dielectric constant of the insulating substance.
Related Chapters
- Physics and Measurement
- Kinematics
- Laws of Motion
- Work, Energy and Power
- Rotational Motion
- Gravitation
- Properties of Solids and Liquids
- Thermodynamics
- Kinetic Theory of Gases
- Oscillations and Waves
- Current Electricity
- Magnetic Effects of Current and Magnetism
- Electromagnetic Induction and Alternating Currents
- Electromagnetic Waves
- Optics
- Dual Nature of Matter and Radiation
- Atoms and Nuclei
- Electronic Devices
- Communication Systems