Class 9 FRANK Solutions Maths Chapter 27: Trigonometrical Ratios of Standard Angles
Complete your revision more effectively with Frank Solutions for ICSE Class 9 Mathematics Chapter 27 Trigonometrical ratios of standard angles. Check out the answers by experts to understand how they have provided proofs or presented an evaluation of trigonometric ratios given in the Frank textbook questions. The expert solutions on TopperLearning can be accessed 24x7 online.
In addition, the Frank solutions for Chapter 27 also provide elaborate answers on finding the angle or side of a triangle using trigonometry. To further revise this ICSE Class 9 Maths chapter or chapters from other syllabus, take a look at our Selina textbook solutions, doubts and solutions, solved question papers, and other useful resources.
Trigonometrical Ratios of Standard Angles Exercise Ex. 27.1
Solution 1
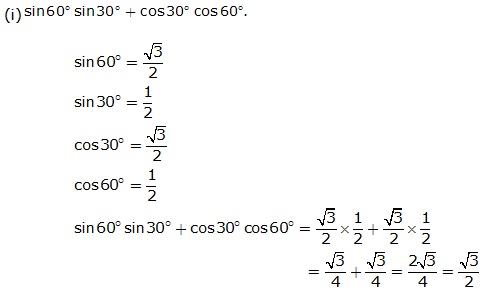
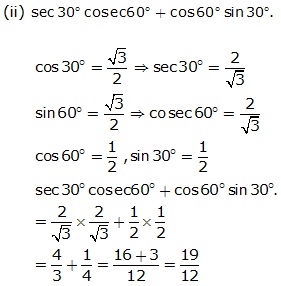
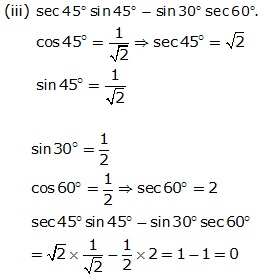
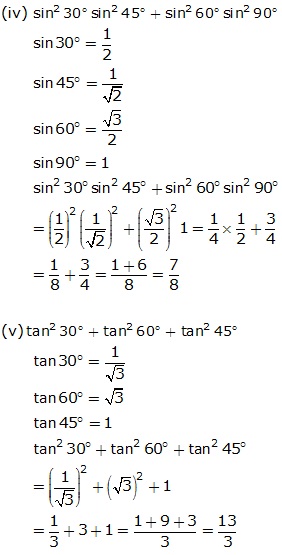
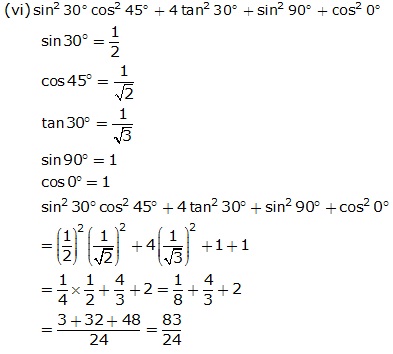
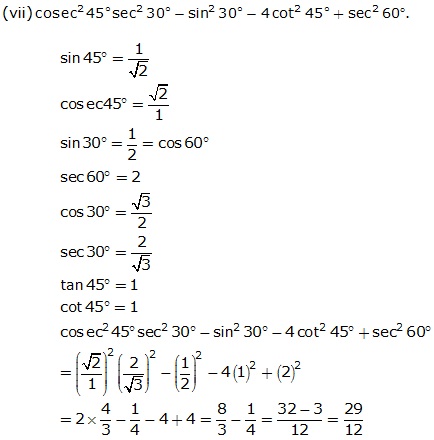

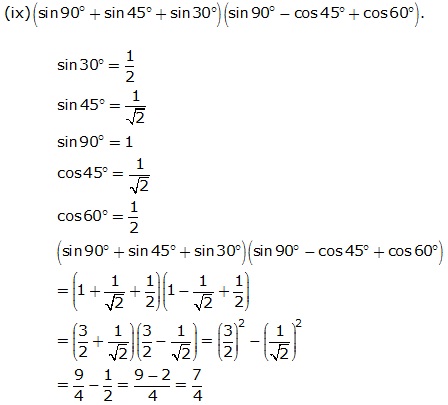
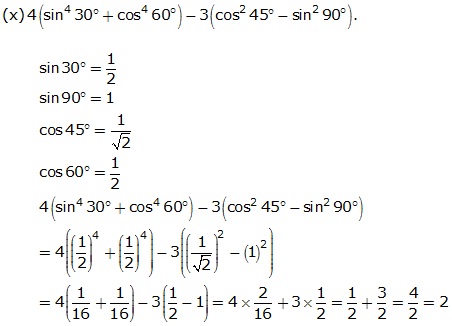
Solution 2
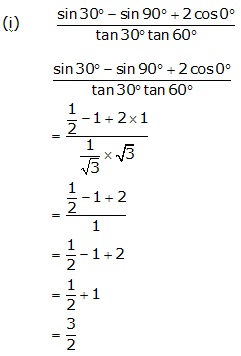
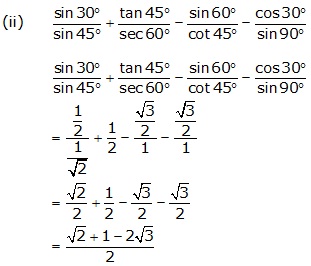
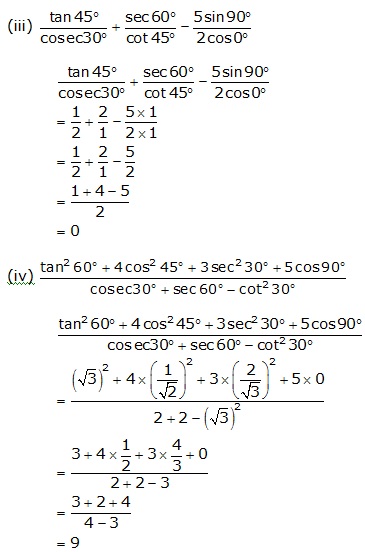
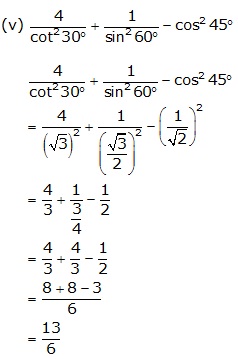
Solution 3(a)
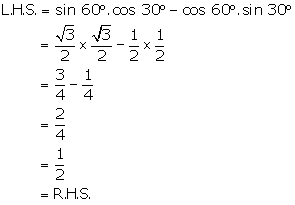
Solution 3(b)
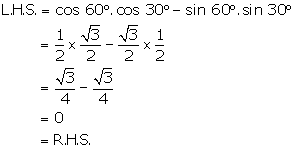
Solution 3(c)
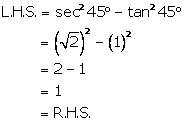
Solution 3(d)

Solution 4(a)
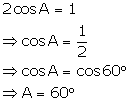
Solution 4(b)
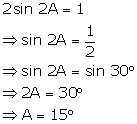
Solution 4(c)
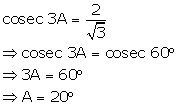
Solution 4(d)
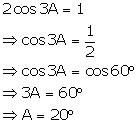
Solution 4(e)
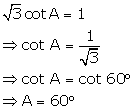
Solution 4(f)

Solution 5(a)

Solution 5(b)

Solution 6
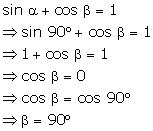
Solution 7(a)
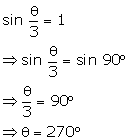
Solution 7(b)

Solution 7(c)
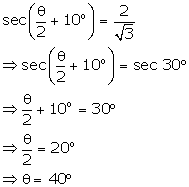
Solution 8
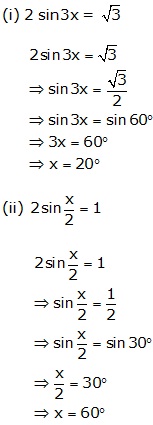
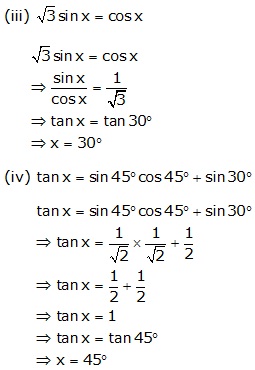
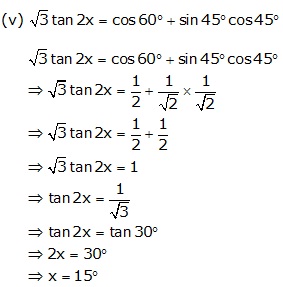
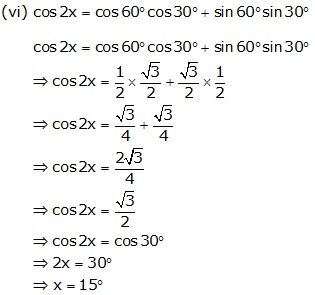
Solution 9
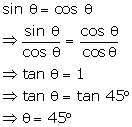
Solution 10
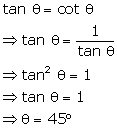
Solution 11

Solution 12(a)
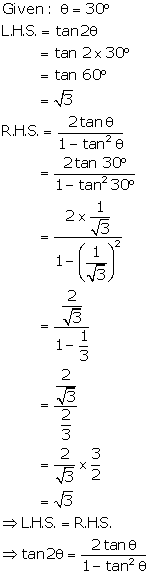
Solution 12(b)
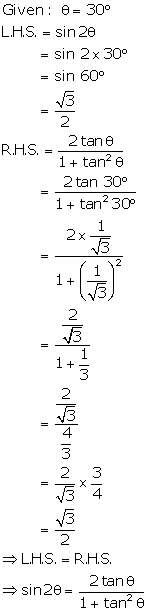
Solution 12(c)
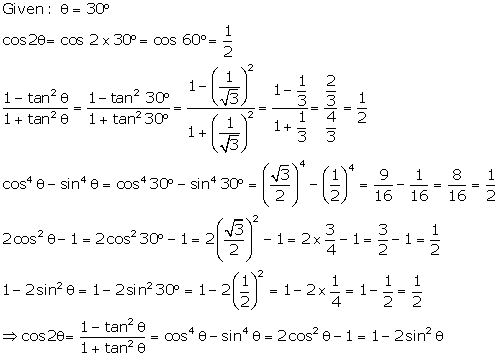
Solution 12(d)
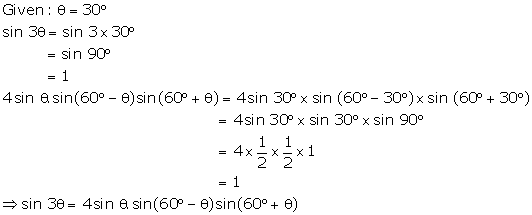
Solution 12(e)
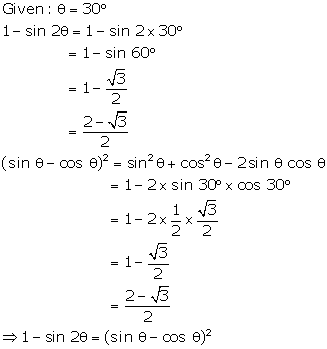
Solution 13(a)

Solution 13(b)

Solution 14
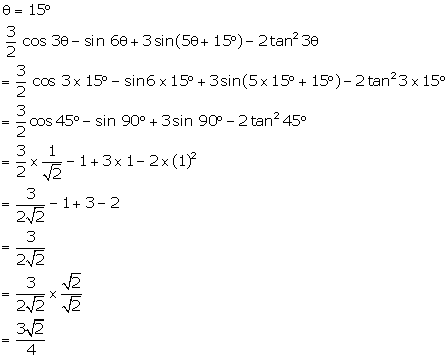
Solution 16(a)
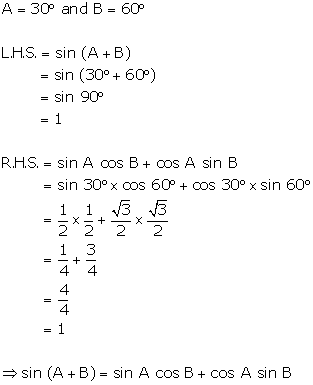
Solution 16(b)
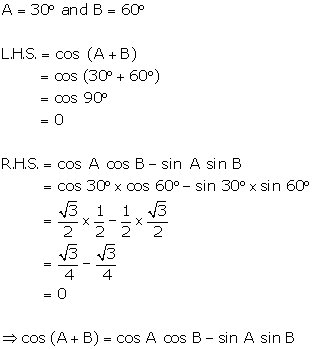
Solution 16(c)
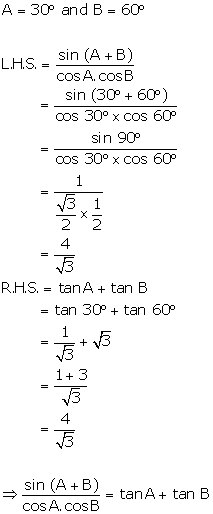
Solution 16(d)
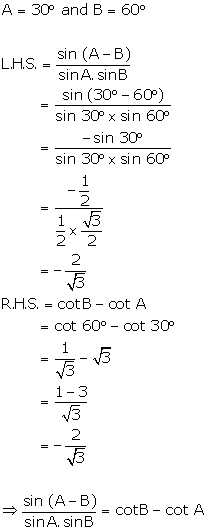
Solution 17(a)
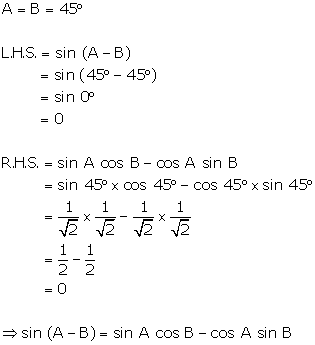
Solution 17(b)
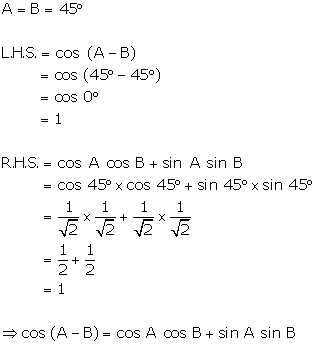
Solution 18
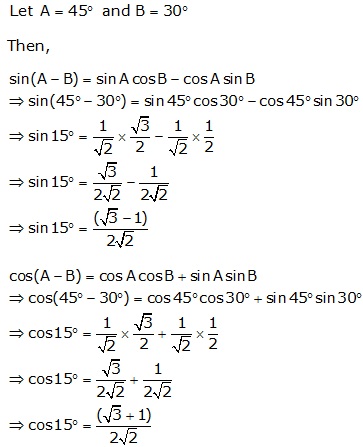
Solution 19(a)

Solution 15



Solution 19(b)
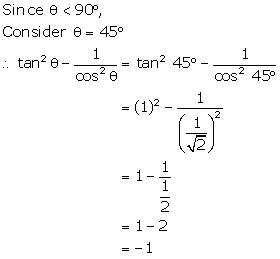
Solution 20(a)
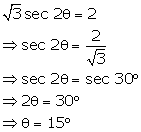
Solution 20(b)
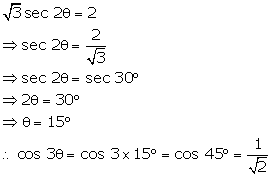
Solution 20(c)
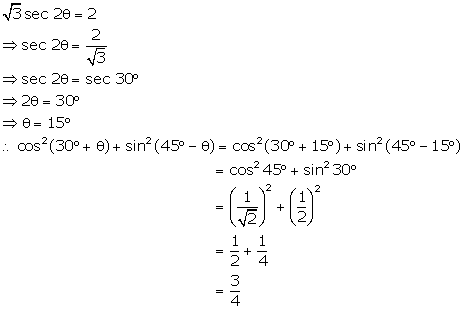
Solution 21
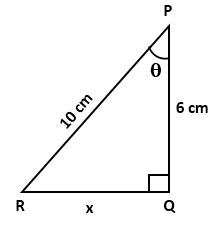
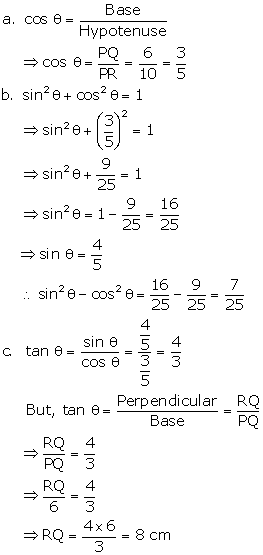
Solution 22
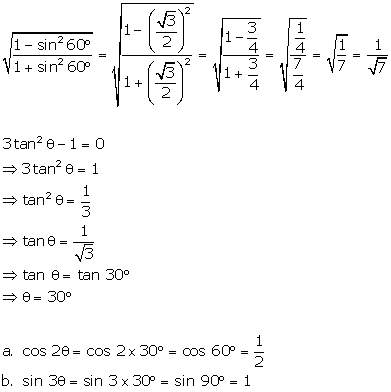
Solution 23

Solution 24

Solution 25

Solution 26
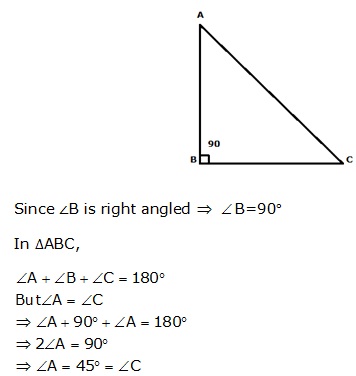
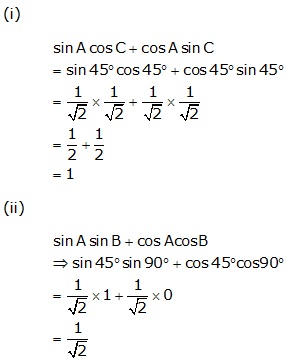
Solution 27
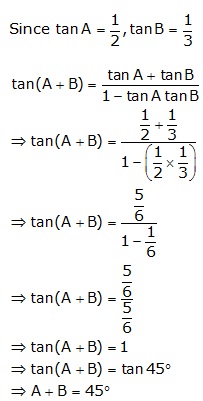
Trigonometrical Ratios of Standard Angles Exercise Ex. 27.2
Solution 14
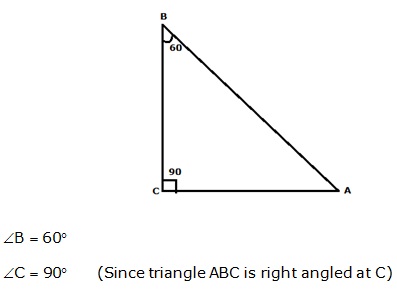
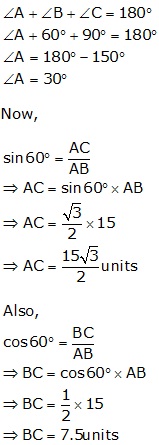
Solution 15
2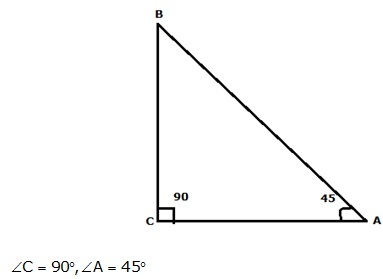
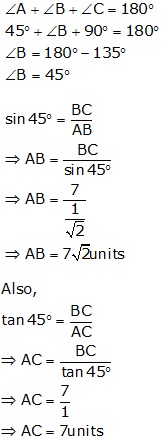
Solution 16
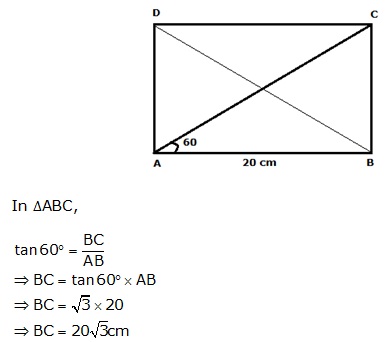
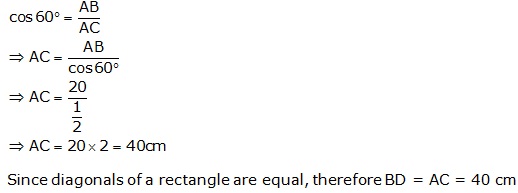
Solution 1(a)
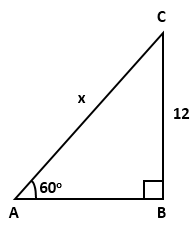
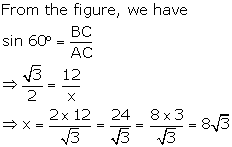
Solution 1(b)
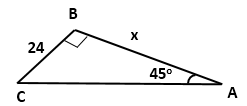
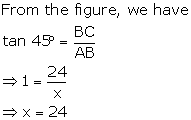
Solution 1(c)
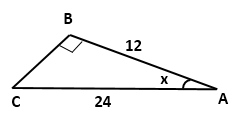
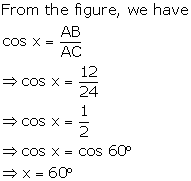
Solution 1(d)
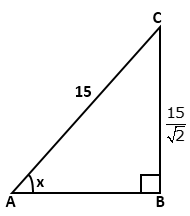

Solution 2
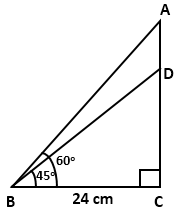

Solution 3
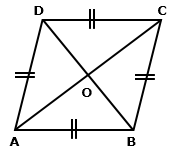

Solution 4
Construction: Draw DP ⊥ AB and CM ⊥ AB
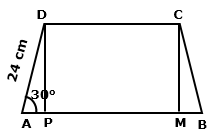

Solution 5
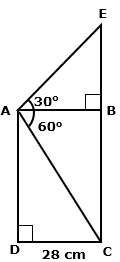

Solution 6
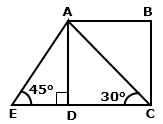

Solution 7
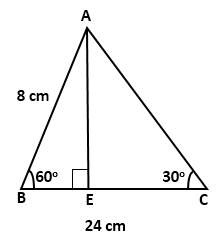

Solution 8

Solution 9(a)
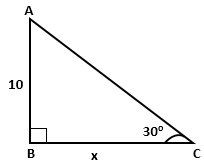
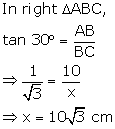
Solution 9(b)
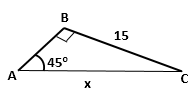
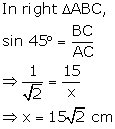
Solution 9(c)

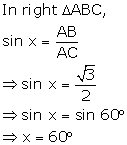
Solution 9(d)
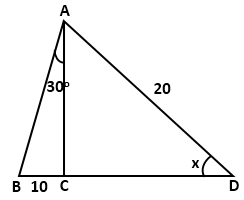
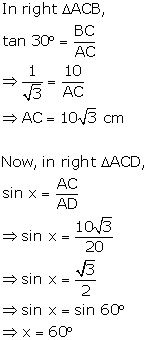
Solution 9(e)
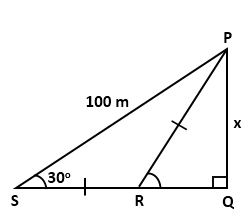
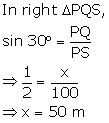
Solution 9(f)


Solution 10(a)
Construction: Draw BX ⊥ AE
Then, BD = EX = 14 cm and BX = ED
AX = AE - EX = 16 - 14 = 2
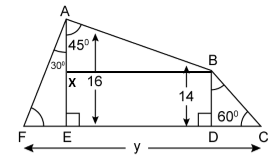

Solution 10(b)


Solution 11
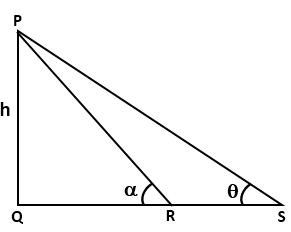
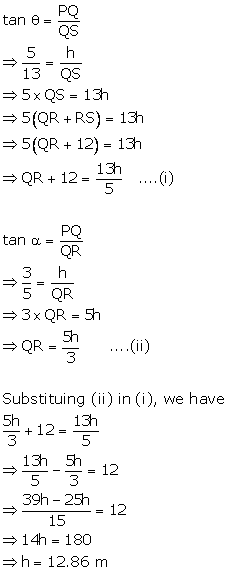
Solution 12(a)
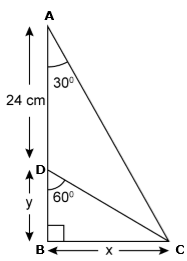
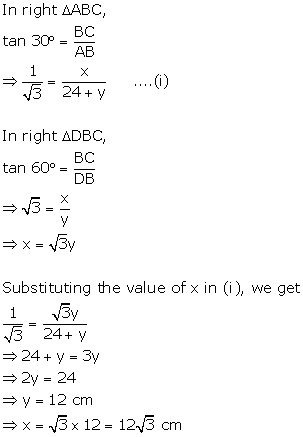
Solution 12(b)
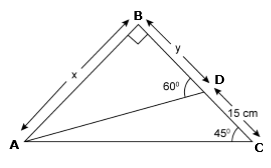

Solution 13

Solution 17
Consider the following figure,

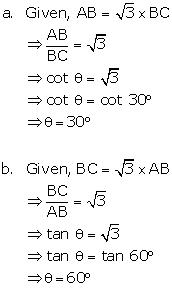
Solution 18

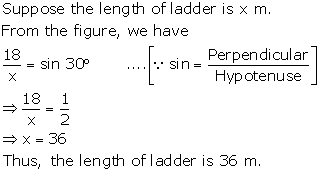
Solution 19
Consider the following figure,
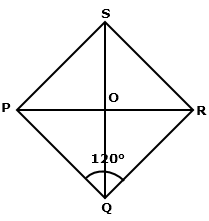

Solution 20
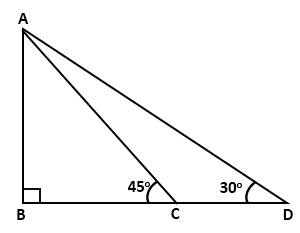

Solution 21
Draw QM ⊥ RS.
Clearly, ∠RQM = 30°
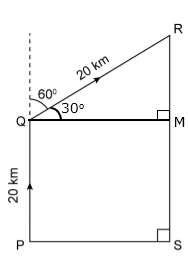

Trigonometrical Ratios of Standard Angles Exercise Ex. 27.3
Solution 1(a)
![]()
Solution 1(b)
![]()
Solution 1(c)
![]()
Solution 1(d)

Solution 1(e)

Solution 1(f)
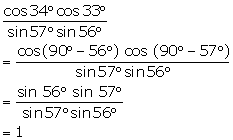
Solution 2(a)

Solution 2(b)
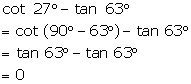
Solution 2(c)
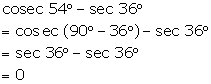
Solution 2(d)

Solution 2(e)
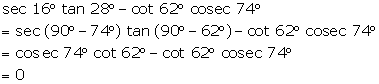
Solution 2(f)

Solution 3(a)

Solution 3(b)
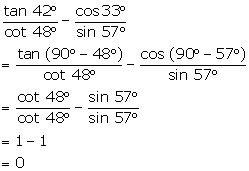
Solution 3(c)
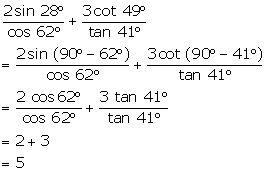
Solution 3(d)

Solution 4(a)
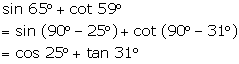
Solution 4(b)

Solution 4(c)
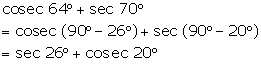
Solution 4(d)

Solution 4(e)

Solution 4(f)
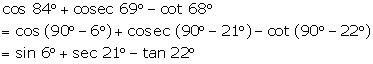
Solution 5(a)

Solution 5(b)
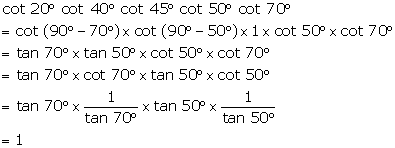
Solution 5(c)
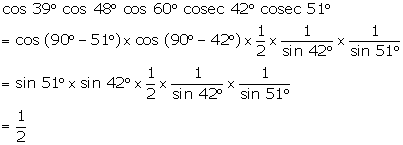
Solution 5(d)
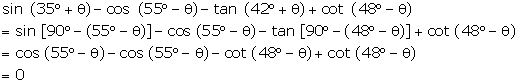
Solution 5(e)
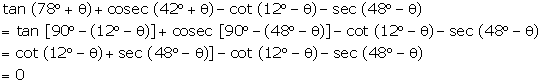
Solution 5(f)
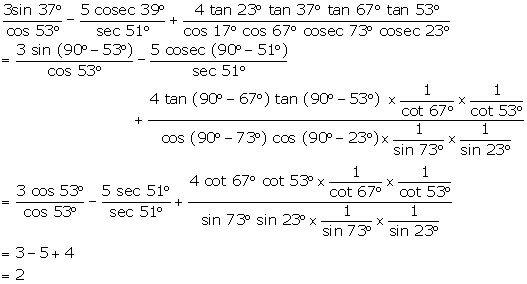
Solution 5(g)

Solution 5(h)

Solution 5(i)
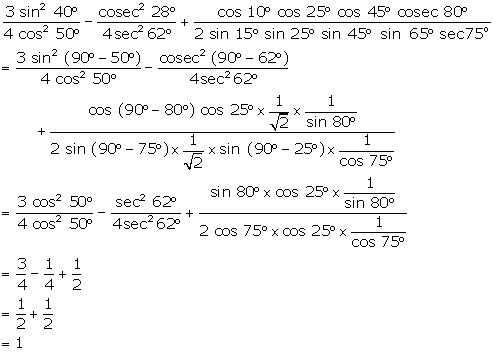
Solution 5(j)

Solution 6
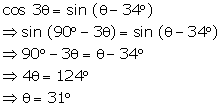
Solution 7
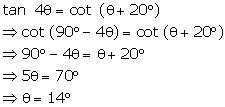
Solution 8
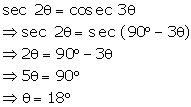
Solution 9
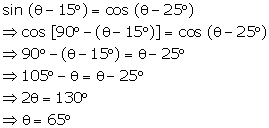
Solution 10

Solution 11

Solution 12
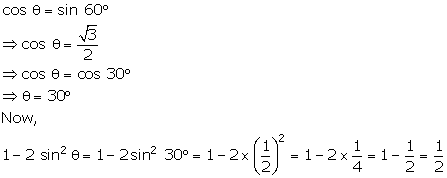
Solution 13
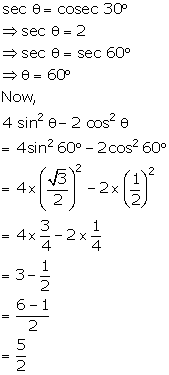
Solution 14(a)
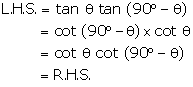
Solution 14(b)
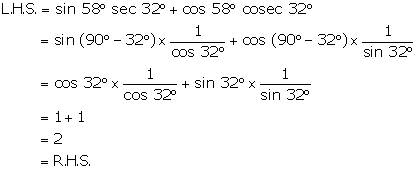
Solution 14(c)
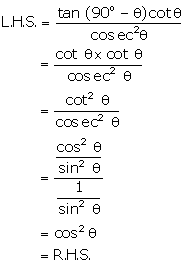
Solution 14(d)

Solution 15

