Class 9 FRANK Solutions Maths Chapter 21: Areas Theorems on Parallelograms
Get quick access to online Frank Solutions for ICSE Class 9 Mathematics Chapter 21 Areas theorems on Parallelograms on TopperLearning. You will learn how to prove theorems in this chapter. You can use the textbook solutions as quick reference materials to revise the lessons.
Learn to use the accurate theorem to find the area of a parallelogram using the information of area of a triangle that’s part of the parallelogram. Revise similar area theorem problems effectively with our ICSE Class 9 Maths Frank solutions. For clarity on quadrilateral problems, you can get your doubts answered in our learning portal’s ‘UnDoubt’ section.
Areas Theorems on Parallelograms Exercise Ex. 21.1
Solution 36
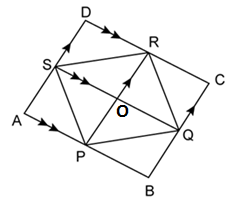
Construction: Join QR. Let the diagonals PR and QS intersect each other at point O.
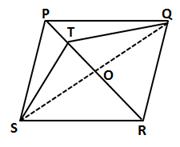
Since diagonals of a parallelogram bisect each other, therefore O is the mid-point of both PR and QS.
Now, median of a triangle divides it into two triangles of equal area.
In ΔPSQ, OP is the median.
∴ Area(ΔPOS) = Area(ΔPOQ) ….(i)
Similarly, OT is the median of ΔTSQ.
∴Area(ΔTOS) = Area(ΔTOQ) ….(ii)
Subtracting equation (ii) from (i), we have
Area(ΔPOS) - Area(ΔTOS) = Area(ΔPOQ) - Area(ΔTOQ)
⇒ Area(ΔPTQ) = Area(ΔPTS)
⇒ Area(ΔPTS) = 18 square units
Solution 35
Construction: Join SM and SQ.
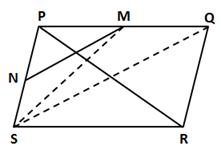
In a parallelogram PQRS, SQ is the diagonal.
So, it bisects the parallelogram.
∴
Area(DPSQ)
![]()
SM is the median of ΔPSQ.
∴
Area(ΔPSM)
![]()
Again, MN is the median of ΔPSM.
∴
Area(ΔPMN)
![]()

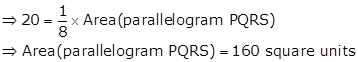
Solution 34(b)
AD is the median of ΔABC.
Therefore it will divide ΔABC into two triangles of equal areas.
∴ Area(ΔABD) = Area(ΔACD) ….(i)
Similarly, ED is the median of ΔEBC.
∴ Area(ΔEBD) = Area(ΔECD) ….(ii)
Subtracting equation (ii) from (i), we have
Area(ΔABD) - Area(ΔEBD) = Area(ΔACD) - Area(ΔECD)
⇒ Area(ΔABE) = Area(ΔACE) ….(iii)
Since E is the mid-point of median AD,
AE = ED
Now,
ΔABE and ΔBED have equal bases and a common vertex B.
∴ Area(ΔABE) = Area(ΔBED) ….(iv)
From (i), (ii), (iii) and (iv), we get
Area(ΔABE) = A(ΔBED) = Area(ΔACE) = Area(ΔEDC) ….(v)
Now,
Area(ΔABC) = Area(ΔABE) + A(ΔBED) + Area(ΔACE) + Area(ΔEDC)
= 4 × Area(ΔABE) [From (v)]
Solution 34(a)
AD is the median of ΔABC.
Therefore it will divide ΔABC into two triangles of equal areas.
∴ Area(ΔABD) = Area(ΔACD) ….(i)
Similarly, ED is the median of ΔEBC.
∴ Area(DEBD) = Area(DECD) ….(ii)
Subtracting equation (ii) from (i), we have
Area(ΔABD) - Area(ΔEBD) = Area(ΔACD) - Area(ΔECD)
⇒ Area(ΔABE) = Area(ΔACE)
Solution 29
SM ∥ PN
⇒ SM ∥ TN
Also, SR ∥ MN
⇒ ST ∥ MN
Hence, SMNT is a parallelogram.
SM ∥ PN
⇒ SM ∥ PO
Also, PS ∥ QM
⇒ PS ∥ OM
Hence, SMOP is a parallelogram.
Now, parallelograms SMNT and SMOP are on the same base SM and between the same parallels SM and PN.
∴ A(parallelogram SMNT) = A(parallelogram SMOP) ….(i)
Similarly, we can show that quadrilaterals PQRS is a parallelogram.
Now, parallelograms PQRS and SMOP are on the same base PS and between the same parallels PS and QM.
∴ A(parallelogram PQRS) = A(parallelogram SMOP) ….(ii)
From (i) and (ii), we have
A(parallelogram SMNT) = A(parallelogram PQRS)
Solution 25
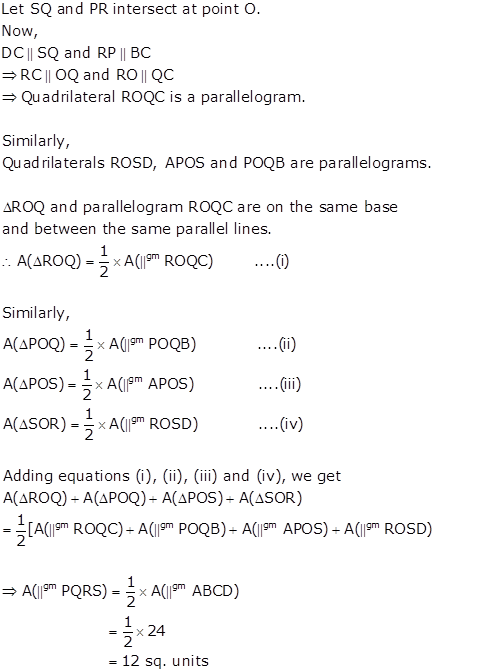
Solution 24

Solution 18
Solution 15

Solution 13

Solution 12
Joining TR, we get
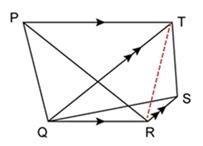
ΔPQR and ΔQTR are on the same base QR and between the same parallel lines QR and PT.
![]()
ΔQTR and ΔTQS are on the same base QT and between the same parallel lines QT and RS.
![]()
From (i) and (ii), we get
![]()
Solution 11
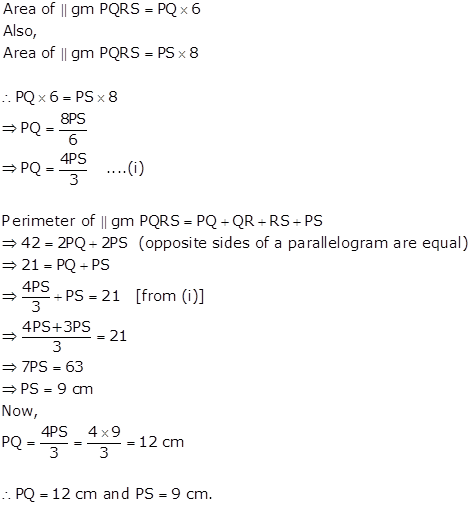
Solution 10
Joining AC and FE, we get
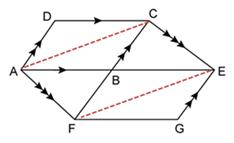
ΔAFC and ΔAFE are on the same base AF and between the same parallels AF and CE.
⇒ A(ΔAFC) = A(ΔAFE)
⇒ A(ΔABF) + A(ΔABC) = A(ΔABF) + A(ΔBFE)
⇒ A(ΔABC) = A(ΔBFE)
⇒ ![]() A(parallelogram ABCD) =
A(parallelogram ABCD) = ![]() A(parallelogram BFGE) ⇒
A(parallelogram ABCD) = A(parallelogram BFGE)
A(parallelogram BFGE) ⇒
A(parallelogram ABCD) = A(parallelogram BFGE)
Solution 6
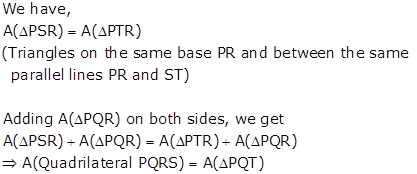
Solution 5
ΔPQT and parallelogram PQRS are on the same base PQ and between the same parallel lines PQ and SR.
![]()
ΔPSN and parallelogram PQRS are on the same base PS and between the same parallel lines PS and QN.
![]()
Adding equations (i) and (ii), we get

Subtracting A(ΔRTN) from both the sides, we get
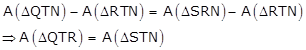
Solution 4
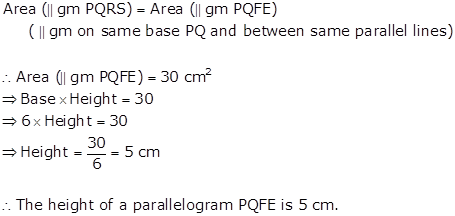
Solution 1
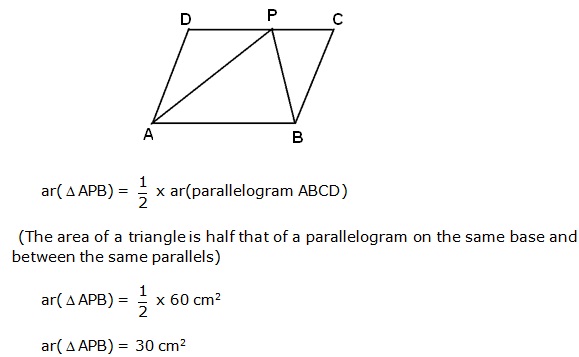
Solution 2
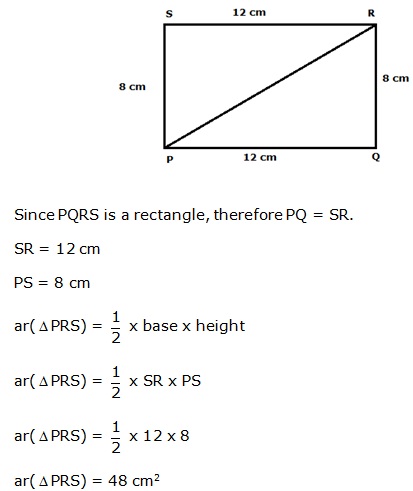
Solution 3


Solution 7

Solution 8

Solution 9

Solution 14

Solution 16
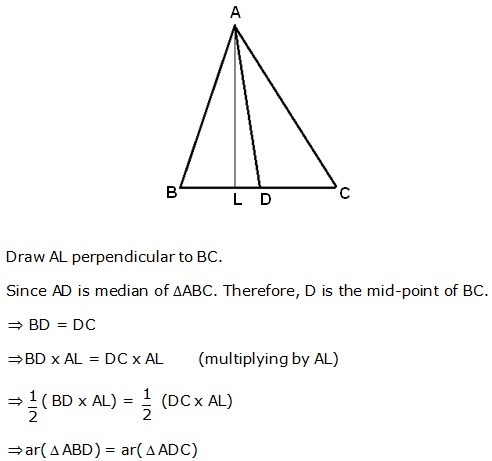
Solution 17
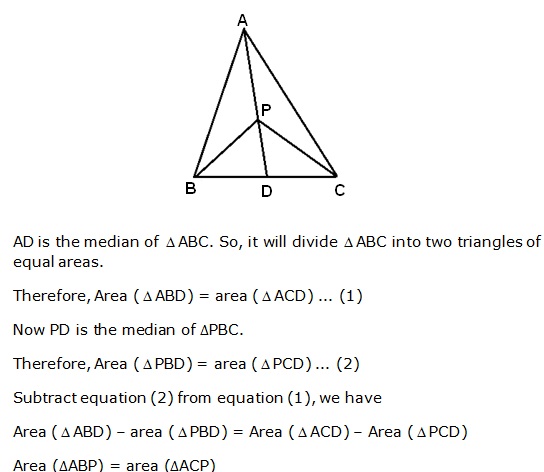
Solution 19
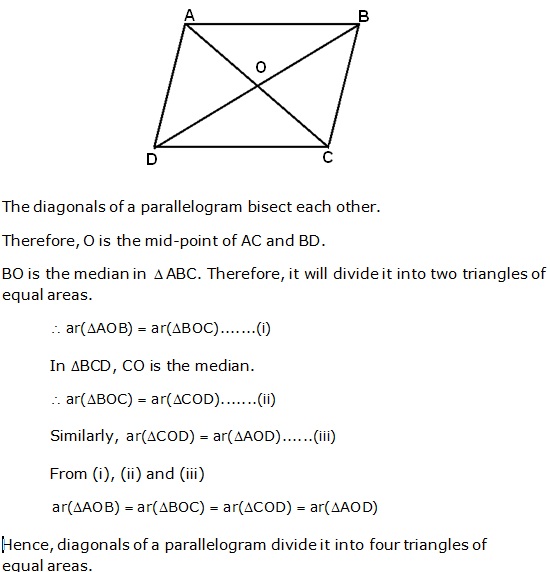
Solution 20
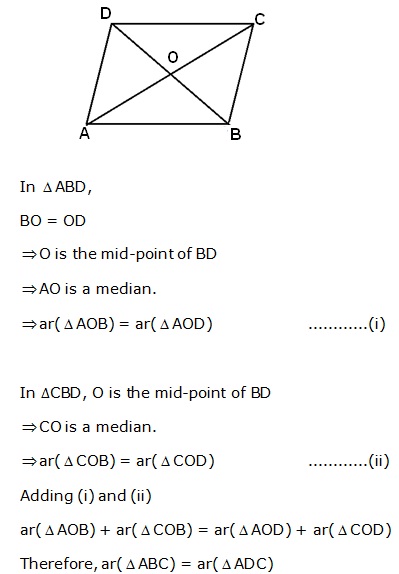
Solution 21
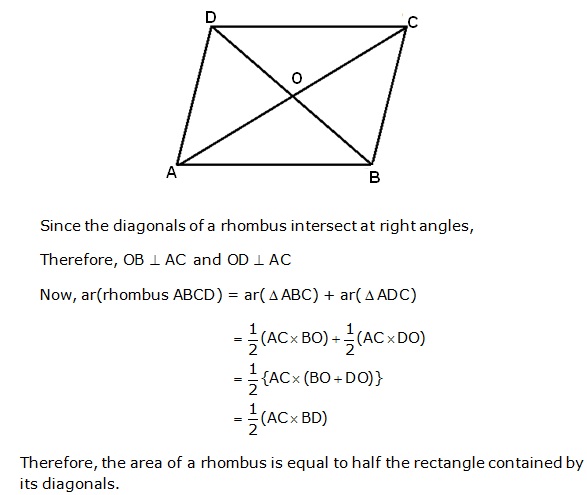
Solution 22




Solution 23
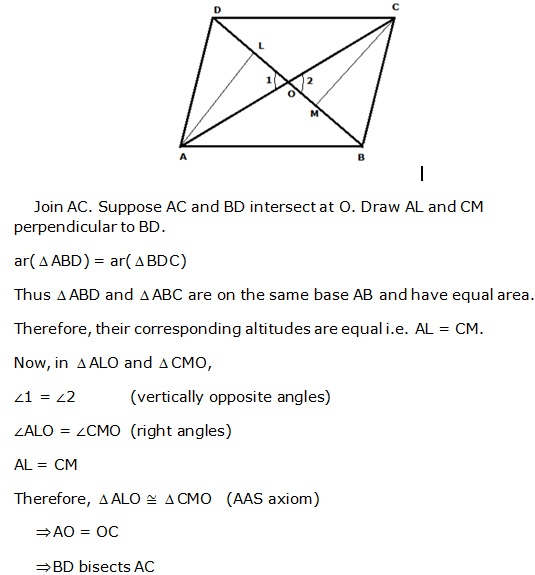
Solution 26
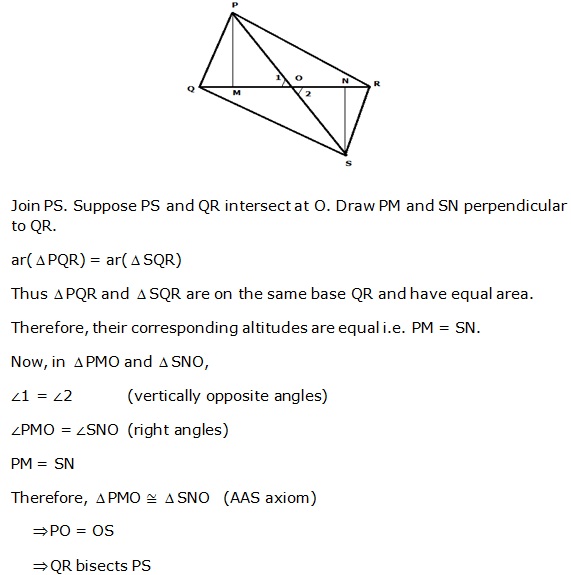
Solution 27
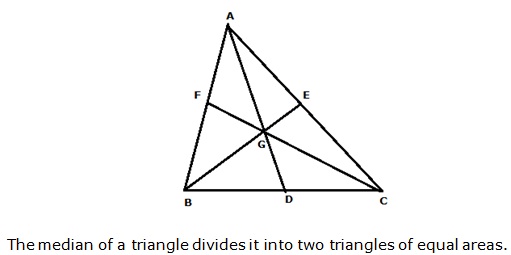

Solution 28
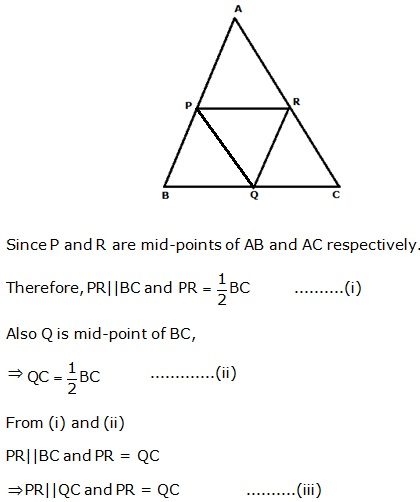


Solution 31


Solution 32

Solution 33
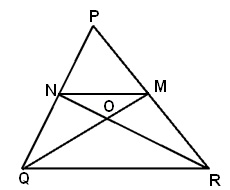

Solution 37


